第三章 导数及其应用 复习课件-湘教版数学选修1-1(27张PPT)
文档属性
| 名称 | 第三章 导数及其应用 复习课件-湘教版数学选修1-1(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 00:00:00 | ||
图片预览







文档简介
第三章 导数及其应用
复习课件
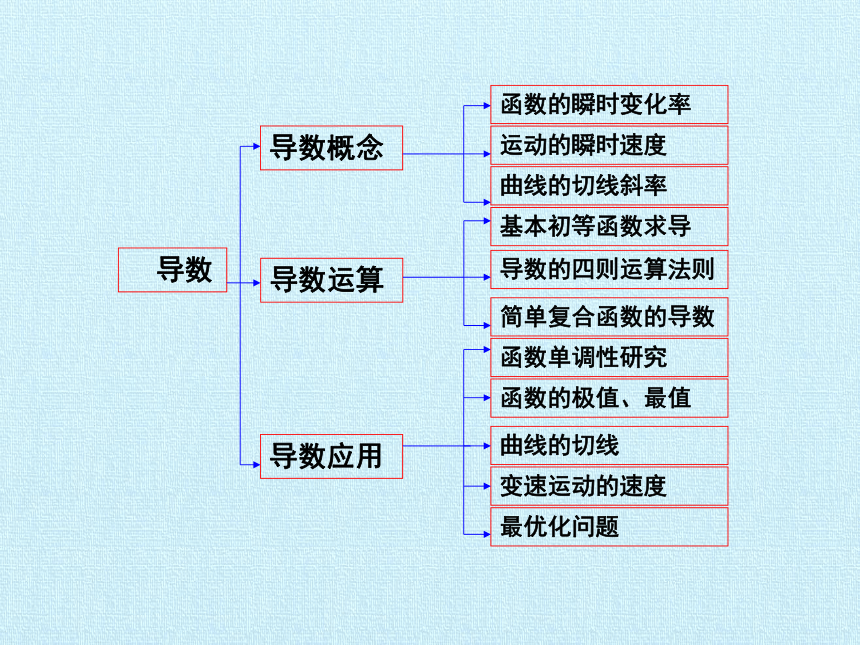
导数
导数概念
导数运算
导数应用
函数的瞬时变化率
运动的瞬时速度
曲线的切线斜率
基本初等函数求导
导数的四则运算法则
简单复合函数的导数
函数单调性研究
函数的极值、最值
曲线的切线
变速运动的速度
最优化问题
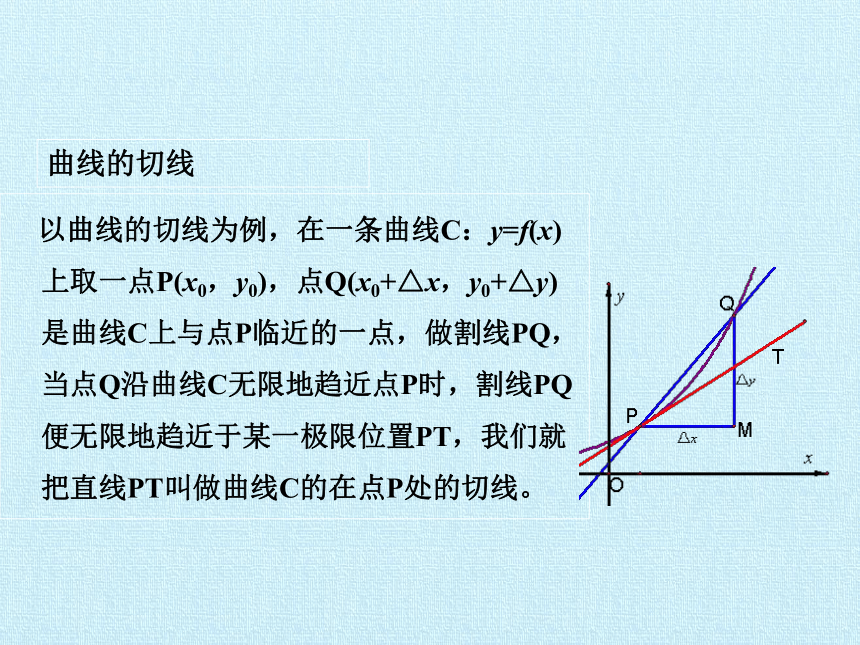
曲线的切线
以曲线的切线为例,在一条曲线C:y=f(x)上取一点P(x0,y0),点Q(x0+△x,y0+△y)是曲线C上与点P临近的一点,做割线PQ,当点Q沿曲线C无限地趋近点P时,割线PQ便无限地趋近于某一极限位置PT,我们就把直线PT叫做曲线C的在点P处的切线。
此时割线PT斜率的极限就是曲线C在点P处的切线的斜率,用极限运算的表达式来写出,即
k=tanα=
导数的概念:
1.导数的定义:对函数y=f(x),在点x=x0处给自变量x以增量△x,函数y相应有增量△y=f(x0+△ x)-f(x0),
若极限 存在,则此极限称为f(x)在点x=x0处的导数,记为f ’(x0),或y| ;
2.导函数:如果函数y=f(x)在区间(a,b)内每一点都可导,就说y=f(x)在区间(a,b)内可导.即对于开区间(a,b)内每一个确定的x0值,都相对应着一个确定的导数f ’(x0),这样在开区间(a,b)内构成一个新函数,把这一新函数叫做f(x)在(a,b)内的导函数.简称导数.记作f ’(x)或y’.
即f ’(x)=y’=
3.导数的几何意义:函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在P(x0,f(x0))处的切线的斜率,即曲线y=f(x)在点P(x0,f(x0))处的切线斜率为k=f ’(x0).所以曲线 y=f(x)在点 P(x0,f(x0))处的切线方程为
y?y0=f ’(x0)·(x-x0).
4.导数的物理意义:物体作直线运动时,路程s关于时间t的函数为:s=s(t),那么瞬时速度 v 就是路程 s 对于时间t的导数,即v(t)=s’(t).
导数的运算法则:
法则1:两个函数的和(差)的导数,等于这两个函数的导数的
和(差),即:
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.
设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.
即:
P
Q
o
x
y
y=f(x)
割线
切线
T
1) 如果恒有 f′(x)>0,那么 y=f(x) 在这个区间(a,b)内单调递增;
2) 如果恒有 f′(x)<0,那么 y=f(x)在这个区间(a,b)内单调递减。
一般地,函数y=f(x)在某个区间(a,b)内
定理
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
如果在某个区间内恒有 ,则 为常数.
2)如果a是f’(x)=0的一个根,并且在a 的左侧附近f’(x)<0,在a 右侧附近f’(x)>0,那么是f(a)函数f(x)的一个极小值.
函数的极值
1)如果b是f’(x)=0的一个根,并且在b左侧附近f’(x)>0,在b右侧附近f’(x)<0,那么f(b)是函数f(x)的一个极大值
注:导数等于零的点不一定是极值点.
2)在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
函数的最大(小)值与导数
x
y
0
a
b
x1
x2
x3
x4
f(a)
f(x3)
f(b)
f(x1)
f(x2)
函数的最大值与最小值:
1.定义:最值是一个整体性概念,是指函数在给定区间(或定义域)内所有函数值中最大的值或最小的值,最大数值叫最大值,最小的值叫最小值,通常最大值记为M,最小值记为m.
2.存在性:在闭区间[a,b]上连续函数f(x)在[a,b]上必有最大值与最小值.
3.求最大(小)值的方法:函数f(x)在闭区间[a,b]上最值求法:
① 求出f(x)在(a,b)内的极值;
② 将函数f(x)的极值与f(a),f(b)比较,其中较大的一个是最大值,较小的一个是最小值.
(1)正确理解导数的概念和意义,导数是一个函数的改变量与自变量的改变量的比值的极限,它反映的是函数的变化率,即函数值在x=x0点附近的变化快慢;所以只有与变化率有关的问题都可以用导数来解决;
(2)掌握求导数的方法,特别是在求复合函数的导数时,一定要把握层次,把每一层的复合关系都看清楚;
(3)利用导数来研究函数。主要是研究函数的增减性、函数的极大(小)值、函数的最大(小)值以及一些与实际相关的问题。
小结:
谢 谢
复习课件
导数
导数概念
导数运算
导数应用
函数的瞬时变化率
运动的瞬时速度
曲线的切线斜率
基本初等函数求导
导数的四则运算法则
简单复合函数的导数
函数单调性研究
函数的极值、最值
曲线的切线
变速运动的速度
最优化问题
曲线的切线
以曲线的切线为例,在一条曲线C:y=f(x)上取一点P(x0,y0),点Q(x0+△x,y0+△y)是曲线C上与点P临近的一点,做割线PQ,当点Q沿曲线C无限地趋近点P时,割线PQ便无限地趋近于某一极限位置PT,我们就把直线PT叫做曲线C的在点P处的切线。
此时割线PT斜率的极限就是曲线C在点P处的切线的斜率,用极限运算的表达式来写出,即
k=tanα=
导数的概念:
1.导数的定义:对函数y=f(x),在点x=x0处给自变量x以增量△x,函数y相应有增量△y=f(x0+△ x)-f(x0),
若极限 存在,则此极限称为f(x)在点x=x0处的导数,记为f ’(x0),或y| ;
2.导函数:如果函数y=f(x)在区间(a,b)内每一点都可导,就说y=f(x)在区间(a,b)内可导.即对于开区间(a,b)内每一个确定的x0值,都相对应着一个确定的导数f ’(x0),这样在开区间(a,b)内构成一个新函数,把这一新函数叫做f(x)在(a,b)内的导函数.简称导数.记作f ’(x)或y’.
即f ’(x)=y’=
3.导数的几何意义:函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在P(x0,f(x0))处的切线的斜率,即曲线y=f(x)在点P(x0,f(x0))处的切线斜率为k=f ’(x0).所以曲线 y=f(x)在点 P(x0,f(x0))处的切线方程为
y?y0=f ’(x0)·(x-x0).
4.导数的物理意义:物体作直线运动时,路程s关于时间t的函数为:s=s(t),那么瞬时速度 v 就是路程 s 对于时间t的导数,即v(t)=s’(t).
导数的运算法则:
法则1:两个函数的和(差)的导数,等于这两个函数的导数的
和(差),即:
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.
设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.
即:
P
Q
o
x
y
y=f(x)
割线
切线
T
1) 如果恒有 f′(x)>0,那么 y=f(x) 在这个区间(a,b)内单调递增;
2) 如果恒有 f′(x)<0,那么 y=f(x)在这个区间(a,b)内单调递减。
一般地,函数y=f(x)在某个区间(a,b)内
定理
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
如果在某个区间内恒有 ,则 为常数.
2)如果a是f’(x)=0的一个根,并且在a 的左侧附近f’(x)<0,在a 右侧附近f’(x)>0,那么是f(a)函数f(x)的一个极小值.
函数的极值
1)如果b是f’(x)=0的一个根,并且在b左侧附近f’(x)>0,在b右侧附近f’(x)<0,那么f(b)是函数f(x)的一个极大值
注:导数等于零的点不一定是极值点.
2)在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
函数的最大(小)值与导数
x
y
0
a
b
x1
x2
x3
x4
f(a)
f(x3)
f(b)
f(x1)
f(x2)
函数的最大值与最小值:
1.定义:最值是一个整体性概念,是指函数在给定区间(或定义域)内所有函数值中最大的值或最小的值,最大数值叫最大值,最小的值叫最小值,通常最大值记为M,最小值记为m.
2.存在性:在闭区间[a,b]上连续函数f(x)在[a,b]上必有最大值与最小值.
3.求最大(小)值的方法:函数f(x)在闭区间[a,b]上最值求法:
① 求出f(x)在(a,b)内的极值;
② 将函数f(x)的极值与f(a),f(b)比较,其中较大的一个是最大值,较小的一个是最小值.
(1)正确理解导数的概念和意义,导数是一个函数的改变量与自变量的改变量的比值的极限,它反映的是函数的变化率,即函数值在x=x0点附近的变化快慢;所以只有与变化率有关的问题都可以用导数来解决;
(2)掌握求导数的方法,特别是在求复合函数的导数时,一定要把握层次,把每一层的复合关系都看清楚;
(3)利用导数来研究函数。主要是研究函数的增减性、函数的极大(小)值、函数的最大(小)值以及一些与实际相关的问题。
小结:
谢 谢
同课章节目录
