导数的应用课件-湘教版数学选修1-1(14张PPT)
文档属性
| 名称 | 导数的应用课件-湘教版数学选修1-1(14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-03 00:00:00 | ||
图片预览






文档简介
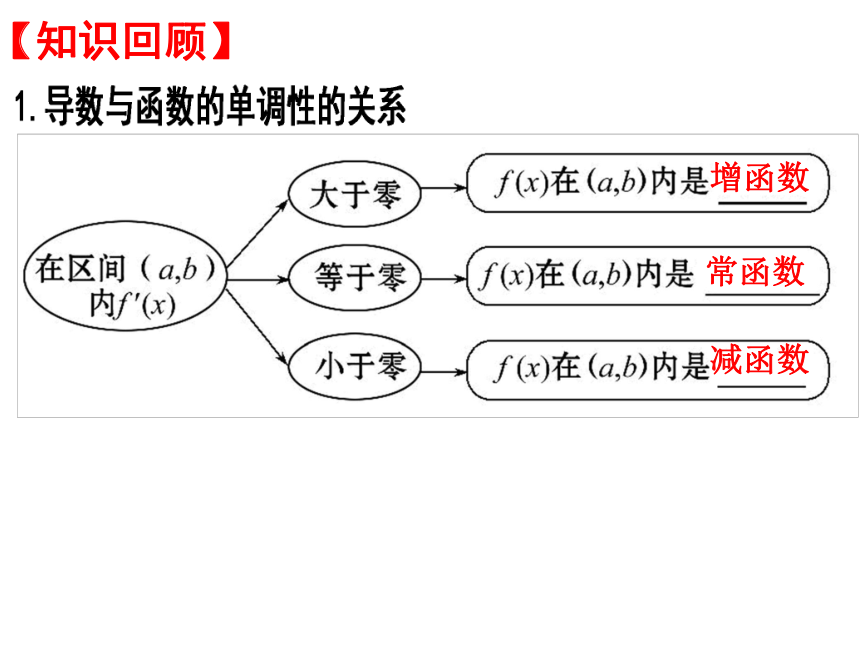
【知识回顾】
增函数
常函数
减函数
【知识回顾】
极大值
极值
极小值
f(a), f(b)
一、利用导数判定函数图象
【小结】
②导数绝对值的大小反映了原函数变化的快慢.
绝对值越大,变化越快,图象越“陡峭”(向上
或向下),反之,变化越慢,图象越“平缓”.
①导数的正(负)反映了原函数的增(减);
【典例剖析】
一、利用导数判定函数图象
【小结】判定函数图象的方法:
1.函数性质法:①从函数的定义域,判断图象 的位置,
从函数的值域, 判断图象 的位置;
②从函数的奇偶性,判断图象的 ;
③从函数的单调性,判断图象的 ;(可借助导数)
④从函数的周期性,判断图象的 ;
⑤从函数的极值点,判断图象的 ;(可借助导数)
⑥从函数的零点, 判断图象与X轴的 ;
2.特殊值检验法:代入特殊值检验
可利用下面方法,排除、筛选错误与正确的选项.
左右
上下
对称性
变化趋势
循环往复
拐点
交点
二、利用导数研究函数零点
【解析】分类讨论法
二、利用导数研究函数零点
【解析】分离参数法
二、利用导数研究函数零点
【解析】分离函数法
二、利用导数研究函数零点
三、利用导数解决不等式恒成立问题
【思路分析】
三、利用导数解决不等式恒成立问题
【总结归纳】
【1】知识与方法:
②利用导数根据函数零点存在情况求参数范围的常见策略:
①利用导数判定函数的图象的常见策略:
直接法、分离参数法、分离函数法、分类讨论法
③利用导数解决不等式恒成立的常见策略:
【2】数学思想
数形结合法、分离参数法、构造函数法
数形结合 、函数与方程、分类讨论、化归与转化等
导函数法、函数性质法、特值检验法
【课后练习】
【课后练习】
感谢各位老师指导
增函数
常函数
减函数
【知识回顾】
极大值
极值
极小值
f(a), f(b)
一、利用导数判定函数图象
【小结】
②导数绝对值的大小反映了原函数变化的快慢.
绝对值越大,变化越快,图象越“陡峭”(向上
或向下),反之,变化越慢,图象越“平缓”.
①导数的正(负)反映了原函数的增(减);
【典例剖析】
一、利用导数判定函数图象
【小结】判定函数图象的方法:
1.函数性质法:①从函数的定义域,判断图象 的位置,
从函数的值域, 判断图象 的位置;
②从函数的奇偶性,判断图象的 ;
③从函数的单调性,判断图象的 ;(可借助导数)
④从函数的周期性,判断图象的 ;
⑤从函数的极值点,判断图象的 ;(可借助导数)
⑥从函数的零点, 判断图象与X轴的 ;
2.特殊值检验法:代入特殊值检验
可利用下面方法,排除、筛选错误与正确的选项.
左右
上下
对称性
变化趋势
循环往复
拐点
交点
二、利用导数研究函数零点
【解析】分类讨论法
二、利用导数研究函数零点
【解析】分离参数法
二、利用导数研究函数零点
【解析】分离函数法
二、利用导数研究函数零点
三、利用导数解决不等式恒成立问题
【思路分析】
三、利用导数解决不等式恒成立问题
【总结归纳】
【1】知识与方法:
②利用导数根据函数零点存在情况求参数范围的常见策略:
①利用导数判定函数的图象的常见策略:
直接法、分离参数法、分离函数法、分类讨论法
③利用导数解决不等式恒成立的常见策略:
【2】数学思想
数形结合法、分离参数法、构造函数法
数形结合 、函数与方程、分类讨论、化归与转化等
导函数法、函数性质法、特值检验法
【课后练习】
【课后练习】
感谢各位老师指导
同课章节目录
