2021-2022学年人教版八年级上 册数学13.2 画轴对称图形 同步测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级上 册数学13.2 画轴对称图形 同步测试卷 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 261.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 08:31:25 | ||
图片预览



文档简介
2021年人教版八上 数学 第十三章 13.2 画轴对称图形 同步测试卷
(总分:120分 考试时间:120分钟)
一、选择题(36分)
(3分)点 M1,2 关于 x 轴对称的点的坐标为 ??
A.?1,?2 B.1,?2 C.?1,2 D.2,?1
(3分)若 Am+2n,2m?n 关于 x 轴对称点是 A5,5,到 Pm,n 的坐标是 ??
A. ?1,?3 B. 1,?3
C. ?1,3 D. 1,3
(3分)如图,△ABC 是边长为 2 的等边三角形,则点 A 关于 x 轴的对称点的坐标为 ??
A. ?1,3 B. ?1,?3
C. 1,3 D. 1,?3
(3分)在平面直角坐标系中,点 P?20,a 与点 Qb,13 关于 x 轴对称,则 a+b 的值为 ??
A. 33 B. ?33 C. ?7 D. 7
(3分)点 P?4,?3 关于 y 轴对称的点的坐标是 ??
A. ?4,3 B. 4,?3
C. 4,3 D. ?3,?4
(3分)如图,在平面直角坐标系 xOy 中,△ABC 的顶点 C3,?1,则点 C 关于 x 轴,y 轴的对称点的坐标分别为 ??
A.3,1,?3,?1 B.?3,1,?3,?1
C.3,1,1,3 D.?3,?1,3,1
(3分)如图,阴影部分是由 5 个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分)是轴对称图形,其中涂法有 ??
A. 6 种 B. 7 种 C. 8 种 D. 9 种
(3分)在直角坐标平面内,已知点 B 和点 A2,3 关于 x 轴对称,点 Cm,n 与点 B 关于原点 O 对称,那么点 C 的坐标为 ??
A. 2,3 B. ?2,?3
C. 2,?3 D. ?2,3
(3分)点 Aa,b 关于 x 轴对称的点 A? 的坐标为 ??
A. a,?b B. ?a,b
C. ?a,?b D. b,a
(3分)若 Am+2n,2m?n 关于 x 轴对称点是 A15,5,则 Pm,n 的坐标是 ??
A. ?1,?3 B. 1,?3
C. ?1,3 D. 1,3
(3分)如图,已知 x 轴是 △AOB 的对称轴,y 轴是 △BOC 的对称轴,点 A 的坐标为 1,2,则点 C 的坐标为 ??
A. -1,-2 B. 1,-2 C. -1,2 D. -2,-1
(3分)如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的个数是 ??
A. 1 B. 2 C. 3 D. 4
二、填空题(24分)
(3分)若点 Am+2,3 与点 B?4,n+5 关于 y 轴对称,则 m+n= .
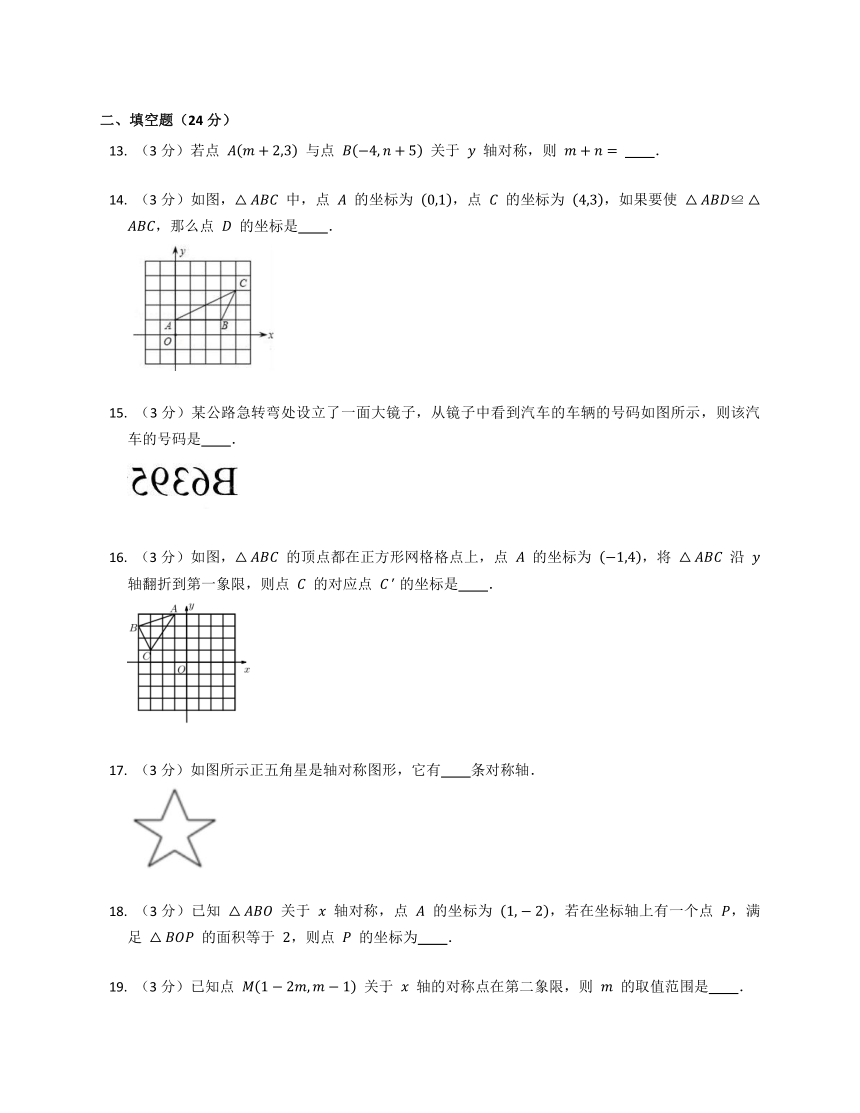
(3分)如图,△ABC 中,点 A 的坐标为 0,1,点 C 的坐标为 4,3,如果要使 △ABD≌△ABC,那么点 D 的坐标是 .
(3分)某公路急转弯处设立了一面大镜子,从镜子中看到汽车的车辆的号码如图所示,则该汽车的号码是 .
(3分)如图,△ABC 的顶点都在正方形网格格点上,点 A 的坐标为 ?1,4,将 △ABC 沿 y 轴翻折到第一象限,则点 C 的对应点 C? 的坐标是 .
(3分)如图所示正五角星是轴对称图形,它有 条对称轴.
(3分)已知 △ABO 关于 x 轴对称,点 A 的坐标为 1,?2,若在坐标轴上有一个点 P,满足 △BOP 的面积等于 2,则点 P 的坐标为 .
(3分)已知点 M1?2m,m?1 关于 x 轴的对称点在第二象限,则 m 的取值范围是 .
(3分)已知点 P1a+1,?5 和点 P26,3?b 关于 y 轴对称,则 a+b99 的值为 .
三、解答题(60分)
(10分)下面的方格图是由边长为 1 的 42 个小正方形拼成的,△ABC 的顶点 A,B,C 均在小正方形的顶点上.
(1) 作出 △ABC 关于直线 m 对称的 △A?B?C?;
(2) 求 △ABC 的面积.
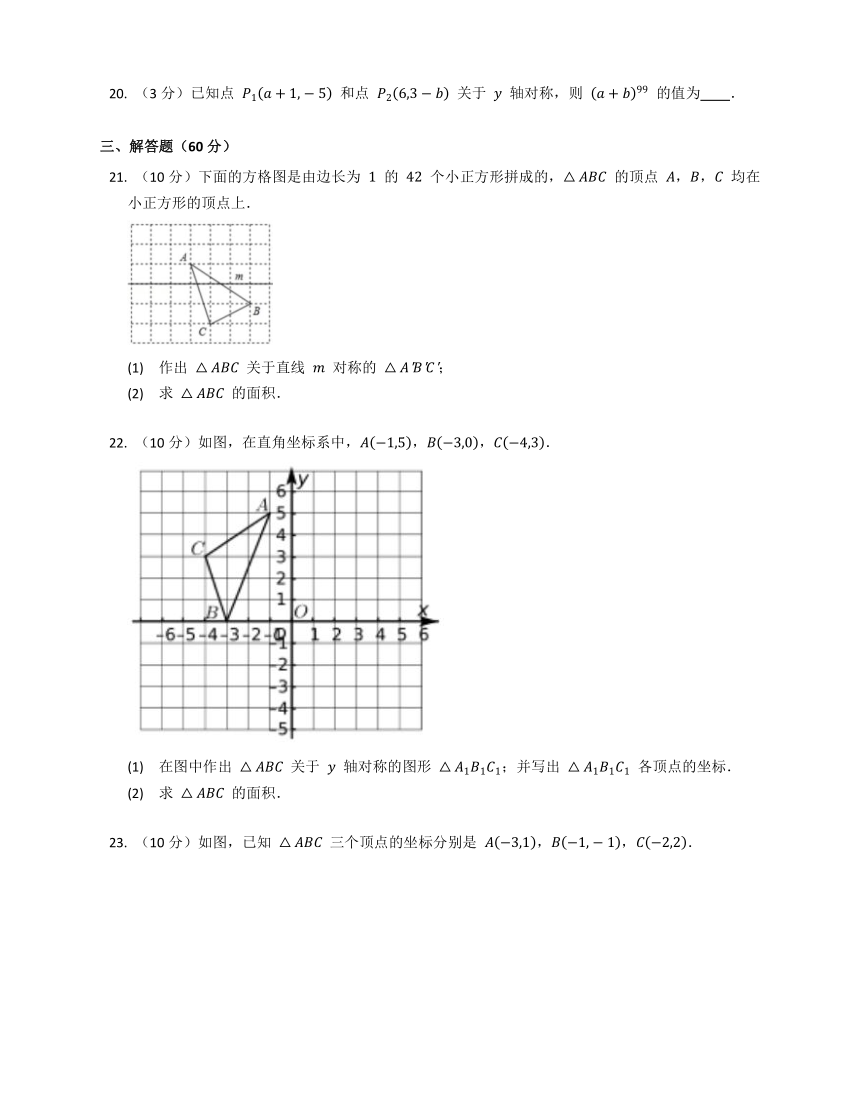
(10分)如图,在直角坐标系中,A?1,5,B?3,0,C?4,3.
(1) 在图中作出 △ABC 关于 y 轴对称的图形 △A1B1C1;并写出 △A1B1C1 各顶点的坐标.
(2) 求 △ABC 的面积.
(10分)如图,已知 △ABC 三个顶点的坐标分别是 A?3,1,B?1,?1,C?2,2.
(1) 画出 △ABC 关于 y 轴对称的 △A1B1C1,并写出点 A1,B1,C1 的坐标.
(2) 画出 △ABC 绕点 B 逆时针旋转 90? 所得到的 △A2B2C2.
(10分)如图,在直角坐标平面内,已知点 A 的坐标为 3,3,点 B 的坐标为 ?4,3,点 P 为直线 AB 上任意一点(不与 A,B 重合),点 Q 是点 P 关于 y 轴的对称点.
(1) △ABO 的面积为 ;
(2) 设点 P 的横坐标为 a,那么点 Q 的坐标为 ;
(3) 设点 P 的横坐标为 13,如果 △OPA 和 △OPQ 的面积相等,且点 P 在点 Q 的右侧,那么应将点 P 向 (填“左”“右”)平移 个单位;
(4) 当 △OPA 的面积是 △OPQ 的面积的 2 倍时,求点 P 的坐标.
(10分)如图,已知 A1,2,B3,1,C4,3.
(1) 作 △ABC 关于 y 轴的对称图形 △A1B1C1,写出点 C1 的坐标;
(2) 直线 m 平行于 x 轴,在直线 m 上求作一点 P,使得 △ABP 的周长最小,请在图中画出 P 点.
(10分)如图,△ABC 中,∠ACB=90?,将 △ABC 沿着一条直线折叠后,使点 A 与点 C 重合(如图②).
(1) 在图①中画出折痕所在的直线 l,问直线 l 是线段 AC 的 线;
(2) 设直线 l 与 AB,AC 分别相交于点 M,N,连接 CM,若 △CMB 的周长是 21?cm,AB=14?cm,求 BC 的长.
答案
一、选择题(36分)
1. 【答案】B
【知识点】坐标平面内图形轴对称变换
2. 【答案】C
【解析】由题意,得 m+2n=5,2m?n=?5,
解得 m=?1,n=3,
故点 P 的坐标为 ?1,3.
【知识点】坐标平面内图形轴对称变换
3. 【答案】D
【知识点】坐标平面内图形轴对称变换
4. 【答案】B
【解析】 ∵ 点 P?20,a 与点 Qb,13 关于 x 轴对称,
∴b=?20,a=?13,
∴a+b=?20+?13=?33.
【知识点】坐标平面内图形轴对称变换
5. 【答案】B
【解析】关于 y 轴对称点的坐标中纵坐标不变,横坐标变为相反数.
【知识点】坐标平面内图形轴对称变换
6. 【答案】A
【知识点】坐标平面内图形轴对称变换
7. 【答案】D
【知识点】画对称轴及轴对称图形
8. 【答案】D
【知识点】坐标平面内图形的旋转变换、坐标平面内图形轴对称变换
9. 【答案】A
【知识点】坐标平面内图形轴对称变换
10. 【答案】C
【解析】 ∵Am+2n,2m?n 关于 x 轴对称点是 A15,5,
∴m+2n=5,2m?n=?5,解得 m=?1,n=3,
∴Pm,n 的坐标是 ?1,3.
【知识点】坐标平面内图形轴对称变换
11. 【答案】A
【知识点】坐标平面内图形轴对称变换
12. 【答案】C
【解析】在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有 5 种等可能的结果,与图中阴影部分构成轴对称图形的有 ②④⑤共 3 种情况,
故选C.
【知识点】画对称轴及轴对称图形
二、填空题(24分)
13. 【答案】 0
【解析】 ∵ 点 Am+2,3 与点 B?4,n+5 关于 y 轴对称,
∴m+2=4,3=n+5,解得:m=2,n=?2,
∴m+n=0.
【知识点】坐标平面内图形轴对称变换
14. 【答案】 (4,?2)
【知识点】坐标平面内图形轴对称变换
15. 【答案】 B6395
【解析】根据镜面对称的性质,题中所显示的图片中的数字与“B6395”成轴对称,则该汽车的号码是 B6395.
【知识点】生活中的轴对称
16. 【答案】 (3,1)
【解析】如图:
∵ 点 A 的坐标为 ?1,4,
∴ 点 C 的坐标为 ?3,1,
∵ 将 △ABC 沿 y 轴翻折到第一象限,
∴ 点 C 的对应点 C? 的坐标是 3,1.
【知识点】坐标平面内图形轴对称变换
17. 【答案】 5
【解析】正五角星的对称轴是过中心和每个顶角的直线,共 5 条.
【知识点】画对称轴及轴对称图形
18. 【答案】 (?2,0);(2,0);(0,4);(0,?4)
【解析】 ∵△ABO 关于 x 轴对称,点 A 的坐标为 1,?2,
∴ 点 B 的坐标为 1,2,
又 ∵ 在坐标轴上有一个点 P,满足 △BOP 的面积等于 2,
∴ 当点 P 在 x 轴上时,12×OP×2=2,即 OP=2,
当点 P 在 y 轴上时,12×OP×1=2,即 OP=4,
∴ 点 P 的坐标为 ?2,0,2,0,0,4,0,?4.
【知识点】坐标平面内图形轴对称变换
19. 【答案】 12【解析】点 M1?2m,m?1 关于 x 轴的对称点为:1?2m,1?m
∵1?2m,1?m 在第二象限,
∴1?2m<0,1?m>0,解得:12【知识点】坐标平面内图形轴对称变换
20. 【答案】 1
【知识点】坐标平面内图形轴对称变换
三、解答题(60分)
21. 【答案】
(1) 如图,△A?B?C? 为所作;
(2) △ABC 的面积 =3×3?12×1×3?12×2×1?12×2×3=3.5.
【知识点】坐标平面内图形的面积、画对称轴及轴对称图形
22. 【答案】
(1) 如图,△A1B1C1 为所作:
点 A1 的坐标为 1,5,
点 B1 的坐标为 3,0,
点 C1 的坐标为 4,3.
(2) △ABC的面积=3×5?12×3×1?12×3×2?12×5×2=112.
【知识点】坐标平面内图形轴对称变换、坐标平面内图形的面积
23. 【答案】
(1) 如图所示.
A13,1,B11,?1,C12,2.
(2) 如图所示.
【知识点】坐标平面内图形的旋转变换、坐标平面内图形轴对称变换
24. 【答案】
(1) 212
(2) (?a,3)
(3) 右;23
(4) ① 当点 P 在 y 轴左侧时,P?1,3;
② 当点 P 在 y 轴右侧时,设点 P 的坐标为 m,3,
则 3?m=2m×2,解得 m=35.
故 P 的坐标为 ?1,3 或 35,3.
【解析】
(1) △ABO 的面积为 12AB?OC=12×7×3=212.
(2) 因为点 P 为直线 AB 上任意一点(不与 A,|(B\)重合),点 Q 是点 P 关于 y 轴的对称点,点 P 的横坐标为 a,
所以点 Q 的坐标是 ?a,3.
(3) 因为 △OPA 和 △OPQ 的面积相等,点 O 到直线 AB 的距离都是 3,
所以线段 AP=PQ.
所以此时点 P 是线段 AQ 的中点,
因为 A3,3,P,Q 关于 y 轴对称,且 P 在 Q 的右侧,
所以 P 的坐标应为 1,3,
所以应将点 P 向右平移 23 个单位.
【知识点】坐标平面内图形轴对称变换、坐标平面内图形的面积、平面直角坐标系及点的坐标、坐标平面内图形的平移变换
25. 【答案】
(1) 如图 1 所示:C1?4,3.
(2) 如图 2 所示:点 P 即为所求.
【知识点】找动点,使距离之和最小、坐标平面内图形轴对称变换
26. 【答案】
(1) 如图①:
垂直平分
(2) ∵ 将 △ABC 沿着一条直线折叠后,使点 A 与点 C 重合,
∴AM=CM,
∵△CMB 的周长是 21?cm,AB=14?cm,
∴21=CM+BM+BC=AM+BM+CB=AB+BC=14+BC,
∴BC=7?cm.
【解析】
(1) ∵ 将 △ABC 沿着一条直线折叠后,使点 A 与点 C 重合,
∴AN=NC,∠ANM=∠CNM=90?.
∴ 直线 l 是线段 AC 的垂直平分线.
【知识点】画对称轴及轴对称图形、垂直平分线的判定、轴对称的性质
(总分:120分 考试时间:120分钟)
一、选择题(36分)
(3分)点 M1,2 关于 x 轴对称的点的坐标为 ??
A.?1,?2 B.1,?2 C.?1,2 D.2,?1
(3分)若 Am+2n,2m?n 关于 x 轴对称点是 A5,5,到 Pm,n 的坐标是 ??
A. ?1,?3 B. 1,?3
C. ?1,3 D. 1,3
(3分)如图,△ABC 是边长为 2 的等边三角形,则点 A 关于 x 轴的对称点的坐标为 ??
A. ?1,3 B. ?1,?3
C. 1,3 D. 1,?3
(3分)在平面直角坐标系中,点 P?20,a 与点 Qb,13 关于 x 轴对称,则 a+b 的值为 ??
A. 33 B. ?33 C. ?7 D. 7
(3分)点 P?4,?3 关于 y 轴对称的点的坐标是 ??
A. ?4,3 B. 4,?3
C. 4,3 D. ?3,?4
(3分)如图,在平面直角坐标系 xOy 中,△ABC 的顶点 C3,?1,则点 C 关于 x 轴,y 轴的对称点的坐标分别为 ??
A.3,1,?3,?1 B.?3,1,?3,?1
C.3,1,1,3 D.?3,?1,3,1
(3分)如图,阴影部分是由 5 个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分)是轴对称图形,其中涂法有 ??
A. 6 种 B. 7 种 C. 8 种 D. 9 种
(3分)在直角坐标平面内,已知点 B 和点 A2,3 关于 x 轴对称,点 Cm,n 与点 B 关于原点 O 对称,那么点 C 的坐标为 ??
A. 2,3 B. ?2,?3
C. 2,?3 D. ?2,3
(3分)点 Aa,b 关于 x 轴对称的点 A? 的坐标为 ??
A. a,?b B. ?a,b
C. ?a,?b D. b,a
(3分)若 Am+2n,2m?n 关于 x 轴对称点是 A15,5,则 Pm,n 的坐标是 ??
A. ?1,?3 B. 1,?3
C. ?1,3 D. 1,3
(3分)如图,已知 x 轴是 △AOB 的对称轴,y 轴是 △BOC 的对称轴,点 A 的坐标为 1,2,则点 C 的坐标为 ??
A. -1,-2 B. 1,-2 C. -1,2 D. -2,-1
(3分)如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的个数是 ??
A. 1 B. 2 C. 3 D. 4
二、填空题(24分)
(3分)若点 Am+2,3 与点 B?4,n+5 关于 y 轴对称,则 m+n= .
(3分)如图,△ABC 中,点 A 的坐标为 0,1,点 C 的坐标为 4,3,如果要使 △ABD≌△ABC,那么点 D 的坐标是 .
(3分)某公路急转弯处设立了一面大镜子,从镜子中看到汽车的车辆的号码如图所示,则该汽车的号码是 .
(3分)如图,△ABC 的顶点都在正方形网格格点上,点 A 的坐标为 ?1,4,将 △ABC 沿 y 轴翻折到第一象限,则点 C 的对应点 C? 的坐标是 .
(3分)如图所示正五角星是轴对称图形,它有 条对称轴.
(3分)已知 △ABO 关于 x 轴对称,点 A 的坐标为 1,?2,若在坐标轴上有一个点 P,满足 △BOP 的面积等于 2,则点 P 的坐标为 .
(3分)已知点 M1?2m,m?1 关于 x 轴的对称点在第二象限,则 m 的取值范围是 .
(3分)已知点 P1a+1,?5 和点 P26,3?b 关于 y 轴对称,则 a+b99 的值为 .
三、解答题(60分)
(10分)下面的方格图是由边长为 1 的 42 个小正方形拼成的,△ABC 的顶点 A,B,C 均在小正方形的顶点上.
(1) 作出 △ABC 关于直线 m 对称的 △A?B?C?;
(2) 求 △ABC 的面积.
(10分)如图,在直角坐标系中,A?1,5,B?3,0,C?4,3.
(1) 在图中作出 △ABC 关于 y 轴对称的图形 △A1B1C1;并写出 △A1B1C1 各顶点的坐标.
(2) 求 △ABC 的面积.
(10分)如图,已知 △ABC 三个顶点的坐标分别是 A?3,1,B?1,?1,C?2,2.
(1) 画出 △ABC 关于 y 轴对称的 △A1B1C1,并写出点 A1,B1,C1 的坐标.
(2) 画出 △ABC 绕点 B 逆时针旋转 90? 所得到的 △A2B2C2.
(10分)如图,在直角坐标平面内,已知点 A 的坐标为 3,3,点 B 的坐标为 ?4,3,点 P 为直线 AB 上任意一点(不与 A,B 重合),点 Q 是点 P 关于 y 轴的对称点.
(1) △ABO 的面积为 ;
(2) 设点 P 的横坐标为 a,那么点 Q 的坐标为 ;
(3) 设点 P 的横坐标为 13,如果 △OPA 和 △OPQ 的面积相等,且点 P 在点 Q 的右侧,那么应将点 P 向 (填“左”“右”)平移 个单位;
(4) 当 △OPA 的面积是 △OPQ 的面积的 2 倍时,求点 P 的坐标.
(10分)如图,已知 A1,2,B3,1,C4,3.
(1) 作 △ABC 关于 y 轴的对称图形 △A1B1C1,写出点 C1 的坐标;
(2) 直线 m 平行于 x 轴,在直线 m 上求作一点 P,使得 △ABP 的周长最小,请在图中画出 P 点.
(10分)如图,△ABC 中,∠ACB=90?,将 △ABC 沿着一条直线折叠后,使点 A 与点 C 重合(如图②).
(1) 在图①中画出折痕所在的直线 l,问直线 l 是线段 AC 的 线;
(2) 设直线 l 与 AB,AC 分别相交于点 M,N,连接 CM,若 △CMB 的周长是 21?cm,AB=14?cm,求 BC 的长.
答案
一、选择题(36分)
1. 【答案】B
【知识点】坐标平面内图形轴对称变换
2. 【答案】C
【解析】由题意,得 m+2n=5,2m?n=?5,
解得 m=?1,n=3,
故点 P 的坐标为 ?1,3.
【知识点】坐标平面内图形轴对称变换
3. 【答案】D
【知识点】坐标平面内图形轴对称变换
4. 【答案】B
【解析】 ∵ 点 P?20,a 与点 Qb,13 关于 x 轴对称,
∴b=?20,a=?13,
∴a+b=?20+?13=?33.
【知识点】坐标平面内图形轴对称变换
5. 【答案】B
【解析】关于 y 轴对称点的坐标中纵坐标不变,横坐标变为相反数.
【知识点】坐标平面内图形轴对称变换
6. 【答案】A
【知识点】坐标平面内图形轴对称变换
7. 【答案】D
【知识点】画对称轴及轴对称图形
8. 【答案】D
【知识点】坐标平面内图形的旋转变换、坐标平面内图形轴对称变换
9. 【答案】A
【知识点】坐标平面内图形轴对称变换
10. 【答案】C
【解析】 ∵Am+2n,2m?n 关于 x 轴对称点是 A15,5,
∴m+2n=5,2m?n=?5,解得 m=?1,n=3,
∴Pm,n 的坐标是 ?1,3.
【知识点】坐标平面内图形轴对称变换
11. 【答案】A
【知识点】坐标平面内图形轴对称变换
12. 【答案】C
【解析】在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,共有 5 种等可能的结果,与图中阴影部分构成轴对称图形的有 ②④⑤共 3 种情况,
故选C.
【知识点】画对称轴及轴对称图形
二、填空题(24分)
13. 【答案】 0
【解析】 ∵ 点 Am+2,3 与点 B?4,n+5 关于 y 轴对称,
∴m+2=4,3=n+5,解得:m=2,n=?2,
∴m+n=0.
【知识点】坐标平面内图形轴对称变换
14. 【答案】 (4,?2)
【知识点】坐标平面内图形轴对称变换
15. 【答案】 B6395
【解析】根据镜面对称的性质,题中所显示的图片中的数字与“B6395”成轴对称,则该汽车的号码是 B6395.
【知识点】生活中的轴对称
16. 【答案】 (3,1)
【解析】如图:
∵ 点 A 的坐标为 ?1,4,
∴ 点 C 的坐标为 ?3,1,
∵ 将 △ABC 沿 y 轴翻折到第一象限,
∴ 点 C 的对应点 C? 的坐标是 3,1.
【知识点】坐标平面内图形轴对称变换
17. 【答案】 5
【解析】正五角星的对称轴是过中心和每个顶角的直线,共 5 条.
【知识点】画对称轴及轴对称图形
18. 【答案】 (?2,0);(2,0);(0,4);(0,?4)
【解析】 ∵△ABO 关于 x 轴对称,点 A 的坐标为 1,?2,
∴ 点 B 的坐标为 1,2,
又 ∵ 在坐标轴上有一个点 P,满足 △BOP 的面积等于 2,
∴ 当点 P 在 x 轴上时,12×OP×2=2,即 OP=2,
当点 P 在 y 轴上时,12×OP×1=2,即 OP=4,
∴ 点 P 的坐标为 ?2,0,2,0,0,4,0,?4.
【知识点】坐标平面内图形轴对称变换
19. 【答案】 12
∵1?2m,1?m 在第二象限,
∴1?2m<0,1?m>0,解得:12
20. 【答案】 1
【知识点】坐标平面内图形轴对称变换
三、解答题(60分)
21. 【答案】
(1) 如图,△A?B?C? 为所作;
(2) △ABC 的面积 =3×3?12×1×3?12×2×1?12×2×3=3.5.
【知识点】坐标平面内图形的面积、画对称轴及轴对称图形
22. 【答案】
(1) 如图,△A1B1C1 为所作:
点 A1 的坐标为 1,5,
点 B1 的坐标为 3,0,
点 C1 的坐标为 4,3.
(2) △ABC的面积=3×5?12×3×1?12×3×2?12×5×2=112.
【知识点】坐标平面内图形轴对称变换、坐标平面内图形的面积
23. 【答案】
(1) 如图所示.
A13,1,B11,?1,C12,2.
(2) 如图所示.
【知识点】坐标平面内图形的旋转变换、坐标平面内图形轴对称变换
24. 【答案】
(1) 212
(2) (?a,3)
(3) 右;23
(4) ① 当点 P 在 y 轴左侧时,P?1,3;
② 当点 P 在 y 轴右侧时,设点 P 的坐标为 m,3,
则 3?m=2m×2,解得 m=35.
故 P 的坐标为 ?1,3 或 35,3.
【解析】
(1) △ABO 的面积为 12AB?OC=12×7×3=212.
(2) 因为点 P 为直线 AB 上任意一点(不与 A,|(B\)重合),点 Q 是点 P 关于 y 轴的对称点,点 P 的横坐标为 a,
所以点 Q 的坐标是 ?a,3.
(3) 因为 △OPA 和 △OPQ 的面积相等,点 O 到直线 AB 的距离都是 3,
所以线段 AP=PQ.
所以此时点 P 是线段 AQ 的中点,
因为 A3,3,P,Q 关于 y 轴对称,且 P 在 Q 的右侧,
所以 P 的坐标应为 1,3,
所以应将点 P 向右平移 23 个单位.
【知识点】坐标平面内图形轴对称变换、坐标平面内图形的面积、平面直角坐标系及点的坐标、坐标平面内图形的平移变换
25. 【答案】
(1) 如图 1 所示:C1?4,3.
(2) 如图 2 所示:点 P 即为所求.
【知识点】找动点,使距离之和最小、坐标平面内图形轴对称变换
26. 【答案】
(1) 如图①:
垂直平分
(2) ∵ 将 △ABC 沿着一条直线折叠后,使点 A 与点 C 重合,
∴AM=CM,
∵△CMB 的周长是 21?cm,AB=14?cm,
∴21=CM+BM+BC=AM+BM+CB=AB+BC=14+BC,
∴BC=7?cm.
【解析】
(1) ∵ 将 △ABC 沿着一条直线折叠后,使点 A 与点 C 重合,
∴AN=NC,∠ANM=∠CNM=90?.
∴ 直线 l 是线段 AC 的垂直平分线.
【知识点】画对称轴及轴对称图形、垂直平分线的判定、轴对称的性质
