2021--2022学年人教版八年级 数学上册13.4 课题学习 最短路径问题 同步测试卷 (word版含答案)
文档属性
| 名称 | 2021--2022学年人教版八年级 数学上册13.4 课题学习 最短路径问题 同步测试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 341.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 08:32:28 | ||
图片预览


文档简介
2021年人教版八上 数学 第十三章 13.4 最短路径问题 同步测试卷
(总分:120分 考试时间:120分钟)
一、选择题(36分)
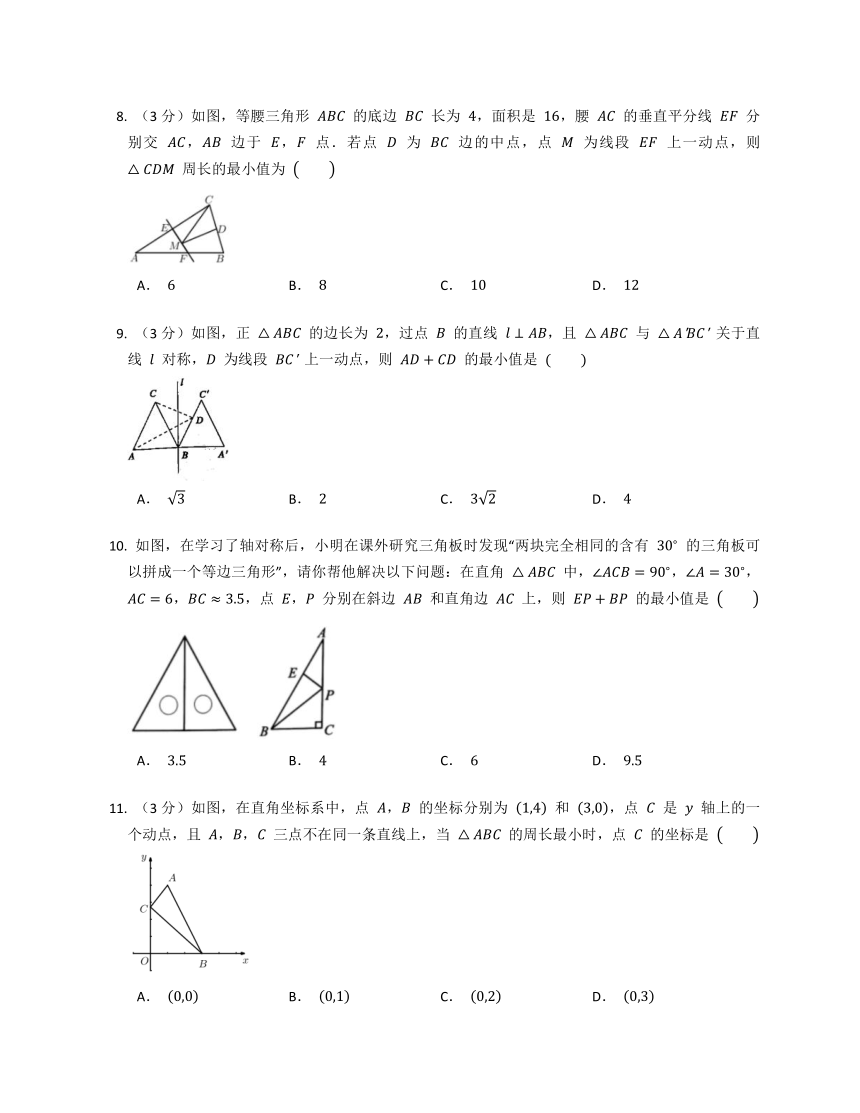
(3分)如图,直线 l 表示一条河,点 A,B 表示两个村庄,想在直线 l 上的某点 P 处修建一个水泵站向 A,B 两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是 ??
A. B.
C. D.
(3分)如图,在锐角 △ABC 中,AB=52,∠BAC=45?,∠BAC 的平分线交 BC 于点 D,若 M,N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小值是 ??
A. 4 B. 5 C. 6 D. 10
(3分)在等边三角形 ABC 中,D,E 分别是 BC,AC 的中点,点 p 是线段 AD 上的一个动点,当 PC+PE 的长最小时,p 点的位置在 ??
A. A 点处 B. AD 的中点处
C. △ABC 的重心处 D. D 点处
(3分)如图,点 P 为 ∠AOB 内一点,分别作点 P 关于 OA,OB 的对称点 P1,P2,连接 P1,P2 交 OA 于 M,交 OB 于 N,若 P1P2=6,则 △PMN 周长为 ??
A. 4 B. 5 C. 6 D. 7
(3分)如图,在 △ABC 中,AB=AC,AB 的垂直平分线交 AB 于 N,交 AC 于 M,P 是直线 MN 上一动点,点 H 为 BC 中点,若 AB=13,△ABC 的周长是 36.则 PB+PH 的最小值为 ??
A. 69 B. 10 C. 12 D. 13
(3分)如图,A,B 是直线 l 外两点,在 l 上求作一点 P,使 PA+PB 最小,其作法是 ??
A.连接 BA 并延长与 l 的交点为 P
B.连接 AB,并作线段 AB 的垂直平分线与 l 的交点为 P
C.过点 B 作 l 的垂线,垂线与 l 的交点为 P
D.过点 A 作 l 的垂线段 AO,O 是垂足,延长 AO 到点 A?,使 A?O=AO,再连接 AB,则 AB 与 l 的交点为 P.
(3分)如图,△ABC 中,AD 垂直 BC 于点 D,且 AD=BC,BC 上方有一动点 P 满足 S△PBC=12S△ABC,则点 P 到 B,C 两点距离之和最小时,∠PBC 的度数为 ??
A. 30? B. 45? C. 60? D. 90?
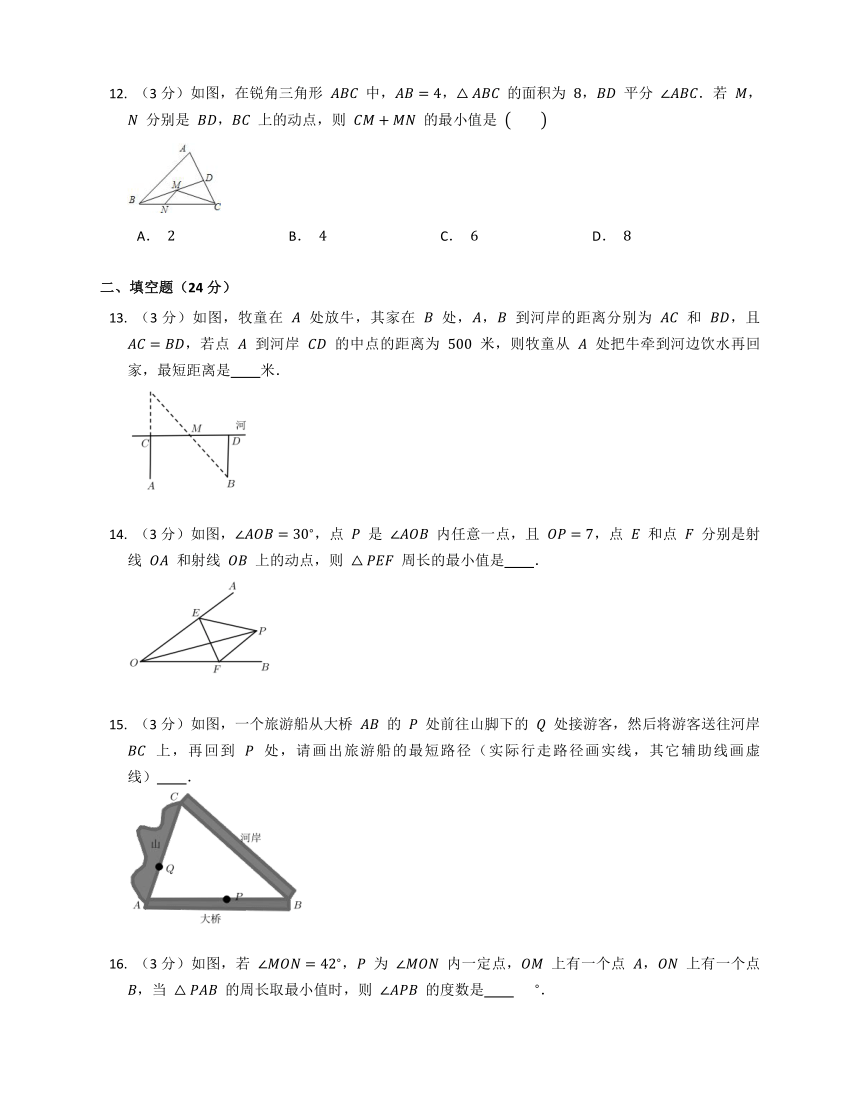
(3分)如图,等腰三角形 ABC 的底边 BC 长为 4,面积是 16,腰 AC 的垂直平分线 EF 分别交 AC,AB 边于 E,F 点.若点 D 为 BC 边的中点,点 M 为线段 EF 上一动点,则 △CDM 周长的最小值为 ??
A. 6 B. 8 C. 10 D. 12
(3分)如图,正 △ABC 的边长为 2,过点 B 的直线 l⊥AB,且 △ABC 与 △A?BC? 关于直线 l 对称,D 为线段 BC? 上一动点,则 AD+CD 的最小值是 (??)
A. 3 B. 2 C. 32 D. 4
如图,在学习了轴对称后,小明在课外研究三角板时发现“两块完全相同的含有 30? 的三角板可以拼成一个等边三角形”,请你帮他解决以下问题:在直角 △ABC 中,∠ACB=90?,∠A=30?,AC=6,BC≈3.5,点 E,P 分别在斜边 AB 和直角边 AC 上,则 EP+BP 的最小值是 ??
A. 3.5 B. 4 C. 6 D. 9.5
(3分)如图,在直角坐标系中,点 A,B 的坐标分别为 1,4 和 3,0,点 C 是 y 轴上的一个动点,且 A,B,C 三点不在同一条直线上,当 △ABC 的周长最小时,点 C 的坐标是 ??
A. 0,0 B. 0,1 C. 0,2 D. 0,3
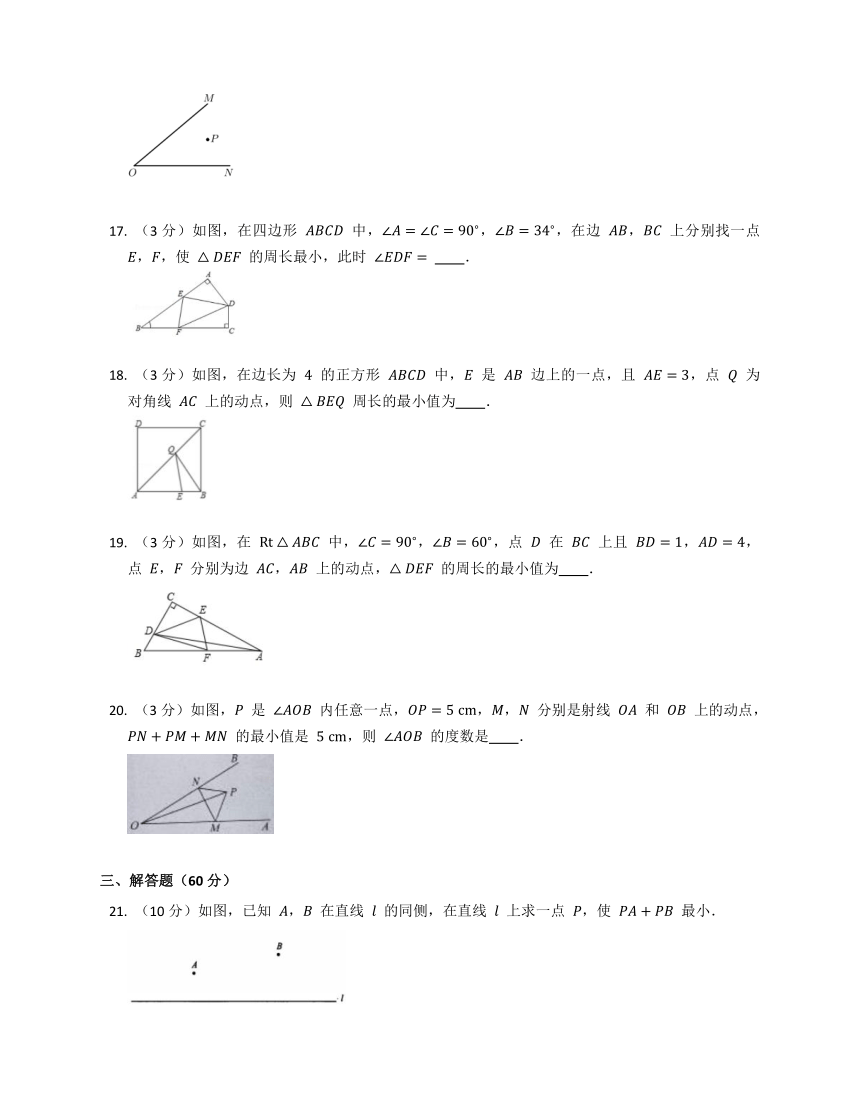
(3分)如图,在锐角三角形 ABC 中,AB=4,△ABC 的面积为 8,BD 平分 ∠ABC.若 M,N 分别是 BD,BC 上的动点,则 CM+MN 的最小值是 ??
A. 2 B. 4 C. 6 D. 8
二、填空题(24分)
(3分)如图,牧童在 A 处放牛,其家在 B 处,A,B 到河岸的距离分别为 AC 和 BD,且 AC=BD,若点 A 到河岸 CD 的中点的距离为 500 米,则牧童从 A 处把牛牵到河边饮水再回家,最短距离是 米.
(3分)如图,∠AOB=30?,点 P 是 ∠AOB 内任意一点,且 OP=7,点 E 和点 F 分别是射线 OA 和射线 OB 上的动点,则 △PEF 周长的最小值是 .
(3分)如图,一个旅游船从大桥 AB 的 P 处前往山脚下的 Q 处接游客,然后将游客送往河岸 BC 上,再回到 P 处,请画出旅游船的最短路径(实际行走路径画实线,其它辅助线画虚线) .
(3分)如图,若 ∠MON=42?,P 为 ∠MON 内一定点,OM 上有一个点 A,ON 上有一个点 B,当 △PAB 的周长取最小值时,则 ∠APB 的度数是 ?.
(3分)如图,在四边形 ABCD 中,∠A=∠C=90?,∠B=34?,在边 AB,BC 上分别找一点 E,F,使 △DEF 的周长最小,此时 ∠EDF= .
(3分)如图,在边长为 4 的正方形 ABCD 中,E 是 AB 边上的一点,且 AE=3,点 Q 为对角线 AC 上的动点,则 △BEQ 周长的最小值为 .
(3分)如图,在 Rt△ABC 中,∠C=90?,∠B=60?,点 D 在 BC 上且 BD=1,AD=4,点 E,F 分别为边 AC,AB 上的动点,△DEF 的周长的最小值为 .
(3分)如图,P 是 ∠AOB 内任意一点,OP=5?cm,M,N 分别是射线 OA 和 OB 上的动点,PN+PM+MN 的最小值是 5?cm,则 ∠AOB 的度数是 .
三、解答题(60分)
(10分)如图,已知 A,B 在直线 l 的同侧,在直线 l 上求一点 P,使 PA+PB 最小.
(10分)如图,在边长为 1 个单位长度的小正方形组成的正方形网格中,点 A,B,C 在小正方形的顶点上.
(1) 在图中画出与 △ABC 关于直线 l 成轴对称的 △A?B?C?;
(2) 线段 CC? 与直线 l 的位置关系是 ;
(3) △ABC 的面积为 ;
(4) 在直线 l 上找一点 P,使 PB+PC 的长最短(标出点 P).
(10分)如图,△ABC 在平面直角坐标系中,点 B 的坐标为 3,?5.
(1) 请在图中画出与 △ABC 关于 x 轴对称的 △A?B?C?,并写出点 A? 的坐标.
(2) 请在图中的 y 轴上画出一点 P,使得 △B?PC? 的周长最短.
(10分)如图所示,有两个村庄 A,B 在一公路 CD 的一侧,如果把 A,B 村庄的位置放在格点图中.
1 请作出 A 点关于 CD 的对称点 A?;
2 若要在公路 CD 上修建一个菜鸟驿站 P,使得驿站到两个村庄的线段距离和最小,请作出 P 点的位置.
(10分)请回答下列问题:
(1) 先化简,再求值:x?y2?yy+2x÷x,其中 ∣x?3∣+y+12=0.
(2) 如图,在单位长度为 1 的正方形网格中,点 A,B,C 都在格点上.
①填空:△ABC 的面积为 ;
②画出 △ABC 关于直线 l 对称的 △A?B?C?,其中点 A,B,C 的对应点分别为 A?,B?,C?;
③在直线 l 上画出一个点 P,使 PA+PC 的值最小.
(10分)如图,方格纸中每个小正方的边长均为 1?cm,四边形 ABCD 的四个顶点都在小正方形的顶点上,点 E 在 BC 边上,且点 E 在小正方形的顶点上,连接 AE.
(1) 在图中画出 △AEF,使 △AEF 与 △AEB 关于直线 AE 对称;
(2) 在图中 AE 上画出点 G,使 △CDG 周长最小;
(3) 连接 FG,请直接写出 △EFG 的面积 cm2.
答案
一、选择题(36分)
1. 【答案】D
【知识点】轴对称之最短路径
2. 【答案】B
【解析】 ∵AD 平分 ∠CAB,
∴ 点 B 关于 AD 的对称点 B? 在线段 AC 上,
作 B?N?⊥AB 于 N? 交 AD 于 M?.
∵BM+MN=B?M+MN,
∴ 当 M 与 M? 重合,N 与 N? 重合时,BM+MN 的值最小,最小值为 B?N?,
∵AD 垂直平分 BB?,
∵AB?=AB=52,
∵∠B?AN?=45?,
∴△AB?N? 是等腰直角三角形,
∴B?N?=5.
∴BM+MN 的最小值为 5.
【知识点】垂直平分线的性质、等腰直角三角形、轴对称之最短路径
3. 【答案】C
【解析】连接 BP,
∵△ABC 是等边三角形,D 是 BC 的中点,
∴AD 是 BC 的垂直平分线,
∴PB=PC,
当 PC+PE 的长最小时,即 PB+PE 最小,
则此时点 B,P,E 在同一直线上时,
又 ∵BE 为中线,
∴ 点 P 为 △ABC 的三条中线的交点,也就是 △ABC 的重心.
【知识点】等边三角形的性质、轴对称之最短路径、三角形的重心
4. 【答案】C
【解析】因为 P 与 P1 关于 OA 对称,
所以 OA 为 PP1 的垂直平分线,
所以 MP=MP1,
P 与 P2 关于 OB 对称,
所以 OB 为 PP2 的垂直平分线,
所以 NP=NP2,
于是 △PMN 周长为 MN+MP+NP=MN+MP1+NP2=P1P2=6.
【知识点】轴对称之最短路径
5. 【答案】C
【知识点】垂直平分线的性质、轴对称之最短路径
6. 【答案】D
【知识点】轴对称之最短路径
7. 【答案】B
【解析】 ∵S△PBC=12S△ABC,
∴P 在与 BC 平行,且到 BC 的距离为 12AD 的直线 l 上,
∴l∥BC,
作点 B 关于直线 l 的对称点 B?,连接 B?C 交 l 于 P,如图所示:
则 BB?⊥l,PB=PB?,此时点 P 到 B,C 两点距离之和最小,
作 PM⊥BC 于 M,则 BB?=2PM=AD,
∵AD⊥BC,AD=BC,
∴BB?=BC,BB?⊥BC,
∴△BB?C 是等腰直角三角形,
∴∠B?=45?,
∵PB=PB?,
∴∠PBB?=∠B?=45?,
∴∠PBC=90??45?=45?.
【知识点】轴对称之最短路径、等腰直角三角形
8. 【答案】C
【解析】连接 AM,
∵△ABC 是等腰三角形,点 D 是 BC 边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×4×AD=16,
解得 AD=8,
∵EF 是线段 AC 的垂直平分线,
∴ 点 C 关于直线 EF 的对称点为点 A,
∴AD 的长为 CM+MD 的最小值,
∴△CDM的周长最短=CM+MD+CD=AD+12BC=8+12×4=8+2=10.
故选C.
【知识点】轴对称之最短路径、等腰三角形的性质、垂直平分线的性质
9. 【答案】D
【解析】连接 CC?,如图所示:
∵△ABC,△A?BC? 均为正三角形,
∴∠ABC=∠A?=60?,A?B=BC=A?C?,
∴A?C?∥BC,
∴ 四边形 A?BCC? 为菱形,
∴ 点 C 关于 BC? 对称的点是 A?,即 CD=A?D,
∴ 当点 D 与点 B 重合时,AD+CD 取最小值,
此时 AD+CD=2+2=4.
【知识点】轴对称之最短路径
10. 【答案】C
【解析】作点 B 关于 AC 的对称点 B?,过 B? 作 B?E 上 AB 交 AC 于点 P,
则 EP+BP 的最小值为 B?E;
由题意可得两块完全相同的含有 30? 的三角板可以拼成一个等边三角形,
又 B?E⊥AB,AC⊥BB?,
故 B?E=AC=6.
【知识点】等边三角形的性质、轴对称之最短路径
11. 【答案】D
【解析】作 B 点关于 y 轴对称点 B? 点,连接 AB?,交 y 轴于点 C?,
此时 △ABC 的周长最小,
∵ 点 A,B 的坐标分别为 1,4 和 3,0,
∴B? 点坐标为:?3,0,AE=4,则 B?E=4,即 B?E=AE,
∵C?O∥AE,
∴B?O=C?O=3,
∴ 点 C? 的坐标是 0,3,此时 △ABC 的周长最小.
【知识点】轴对称之最短路径、平行线的性质
12. 【答案】B
【解析】过点 C 作 CE⊥AB 于点 E,交 BD 于点 M?,过点 M 作 MN?⊥BC 于 N?,
∵BD 平分 ∠ABC,M?E⊥AB 于点 E,M?N?⊥BC 于 N
∴M?N?=M?E,
∴CE=CM?+M?E
∴ 当点 M 与 M? 重合,点 N 与 N? 重合时,CM+MN 的最小值.
∵ 三角形 ABC 的面积为 8,AB=4,
∴12×4?CE=8,
∴CE=4.即 CM+MN 的最小值为 4.
【知识点】轴对称之最短路径、角平分线的性质
二、填空题(24分)
13. 【答案】 1000
【解析】作出 A 的对称点 A?,连接 A?B 与 CD 相交于 M,
则牧童从 A 处把牛牵到河边饮水再回家,最短距离是 A?B 的长.
易得 △A?CM≌△BDM,AC=BD,
∴A?C=BD,则 A?CBD=CMMD,
∴CM=DM,M 为 CD 的中点,
由于 A 到河岸 CD 的中点的距离为 500 米,
∴A? 到 M 的距离为 500 米,A?B=1000 米.
故最短距离是 1000 米.
【知识点】轴对称之最短路径、全等三角形的性质与判定
14. 【答案】 7
【解析】分别作点 P 关于 OA,OB 的对称点 C,D,
连接 CD,分别交 OA,OB 于点 E,F,
连接 OP,OC,OD,PE,PF,
∵ 点 P 关于 OA 的对称点为 C,
∴PE=CE,OP=OC,∠COA=∠POA,
∵ 点 P 关于 OB 的对称点为 D,
∴PF=DF,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=5cm,
∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2,
∠AOB=60?,
∴△COD 是等边三角形,
∴CD=OC=OD=5cm,
∴△PEF 的周长的最小值 =PE+EF+PF=CE+EF+DF≥CD=7.
【知识点】等边三角形的判定、轴对称之最短路径
15. 【答案】如图所示:
【解析】如图所示,作点 P 关于 BC 的对称点 P?,连接 P?Q 交 BC 于点 M,连接 MP.
最短路径为:P?Q?M?P.
【知识点】轴对称之最短路径
16. 【答案】 96
【解析】分别作点 P 关于 ON,OM 的对称点 P?,P?,
连接 OP?,OP?,P?P?,P?P? 交 OM,ON 于点 A,B,连接 PA,PB,
此时 △PAB 周长的最小值等于 P?P?.
由轴对称性质可得,OP?=OP?=OP,∠P?OA=∠POA,
∠P?OB=∠POB,
∴∠P?OP?=2∠MON=2×42?=84?,
∴∠OP?P?=∠OP?P?=180??84?÷2=48?,
又 ∵∠BPO=∠OP?B=48?,∠APO=∠AP?O=48?,
∴∠APB=∠APO+∠BPO=96?.
【知识点】轴对称之最短路径、轴对称的性质
17. 【答案】 112°
【解析】如图,作点 D 关于 BA 的对称点 P,点 D 关于 BC 的对称点 Q,连接 PQ,交 AB 于 E?,交 BC 于 F?,则点 E?,F? 即为所求.
∵ 四边形 ABCD 中,∠A=∠C=90?,∠B=α,
∴∠ADC=180??α,
由轴对称知,∠ADE?=∠P,∠CDF?=∠Q,
在 △PDQ 中,
∠P+∠Q=180??∠ADC=180??180??34?=34?,
∴∠ADE?+∠CDF?=∠P+∠Q=34?,
∴∠E?DF?=∠ADC?∠ADE?+∠CDF?=180??68?=112?.
【知识点】三角形的内角和、轴对称之最短路径
18. 【答案】 6
【解析】连接 BD,DE,
∵ 四边形 ABCD 是正方形,
∴ 点 B 与点 D 关于直线 AC 对称,
∴DE 的长即为 BQ+QE 的最小值,
∵DE=BQ+QE=AD2+AE2=42+32=5,
∴△BEQ周长的最小值=DE+BE=5+1=6.
故答案为 6.
【知识点】轴对称之最短路径
19. 【答案】 4
【解析】如图,作点 D 关于直线 AC 的对称点 D?,点 D 关于直线 AB 的对称点 D?,连接 D?D? 交 AC 于 E,交 AB 于 F,此时 △DEF 的周长最小,最小值为 D?D? 的长,连接 AD?,AD?,
在 Rt△ABC 中,∠C=90?,∠B=60?,
∴∠BAC=30?,
∵∠DAB=∠D?AB,∠DAC=D?AC,
∴∠D?AD?=2∠BAC=60?,
∴△AD?D? 是等边三角形,
∵AD?=AD=4,
∴D?D?=4,
∴△DEF 的周长的最小值为 4.
故答案为 4.
【知识点】等边三角形的判定、轴对称之最短路径
20. 【答案】 30?
【知识点】轴对称之最短路径、等边三角形的判定
三、解答题(60分)
21. 【答案】在直线 l 的另一侧找出点 A 的对称点 A?,连接 A?B 交 l 于 P 点即为所求.
【知识点】轴对称之最短路径
22. 【答案】
(1) 画图略.
(2) 直线 l 垂直平分线段 CC?
(3) 3
(4) 画图略.
【知识点】图形成轴对称、坐标平面内图形轴对称变换、坐标平面内图形的面积、轴对称之最短路径
23. 【答案】
(1) ?3,2,如图所示.
(2) 如图,点 P 即为所求.
【知识点】轴对称之最短路径、坐标平面内图形轴对称变换
24. 【答案】 1 如图所示:A? 点即为所求;
2 如图所示:点 P 即为所求.
【知识点】坐标平面内图形轴对称变换、轴对称之最短路径
25. 【答案】
(1) 原式=x2?2xy+y2?y2?2xy÷x=x2?4xy÷x=x?4y,
由 ∣x?3∣+y+12=0,
得到 x?3=0,y+1=0,
解得:x=3,y=?1,
则 原式=3+4=7.
(2) ① 2
②如图所示,即为所求;
③如图所示,即为所求.
【解析】
(2) ①根据题意得:S△ABC=12×2×2=2.
【知识点】轴对称图形、轴对称之最短路径、整式的加减乘除混合运算
26. 【答案】
(1) 如图 1 所示,
△AEF 即为所求.
(2) 如图 2 所示,作点 D 关于 AE 的对称点 D?,
连接 CD? 交 AE 于点 G,
∴DG=D?G,
此时 △CDG 的周长最小,
点 G 即为所求.
(3) 3
【解析】
(3) △EFG 的面积为 12×6×1=3cm2.
【知识点】画对称轴及轴对称图形、三角形的面积、轴对称之最短路径
(总分:120分 考试时间:120分钟)
一、选择题(36分)
(3分)如图,直线 l 表示一条河,点 A,B 表示两个村庄,想在直线 l 上的某点 P 处修建一个水泵站向 A,B 两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是 ??
A. B.
C. D.
(3分)如图,在锐角 △ABC 中,AB=52,∠BAC=45?,∠BAC 的平分线交 BC 于点 D,若 M,N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小值是 ??
A. 4 B. 5 C. 6 D. 10
(3分)在等边三角形 ABC 中,D,E 分别是 BC,AC 的中点,点 p 是线段 AD 上的一个动点,当 PC+PE 的长最小时,p 点的位置在 ??
A. A 点处 B. AD 的中点处
C. △ABC 的重心处 D. D 点处
(3分)如图,点 P 为 ∠AOB 内一点,分别作点 P 关于 OA,OB 的对称点 P1,P2,连接 P1,P2 交 OA 于 M,交 OB 于 N,若 P1P2=6,则 △PMN 周长为 ??
A. 4 B. 5 C. 6 D. 7
(3分)如图,在 △ABC 中,AB=AC,AB 的垂直平分线交 AB 于 N,交 AC 于 M,P 是直线 MN 上一动点,点 H 为 BC 中点,若 AB=13,△ABC 的周长是 36.则 PB+PH 的最小值为 ??
A. 69 B. 10 C. 12 D. 13
(3分)如图,A,B 是直线 l 外两点,在 l 上求作一点 P,使 PA+PB 最小,其作法是 ??
A.连接 BA 并延长与 l 的交点为 P
B.连接 AB,并作线段 AB 的垂直平分线与 l 的交点为 P
C.过点 B 作 l 的垂线,垂线与 l 的交点为 P
D.过点 A 作 l 的垂线段 AO,O 是垂足,延长 AO 到点 A?,使 A?O=AO,再连接 AB,则 AB 与 l 的交点为 P.
(3分)如图,△ABC 中,AD 垂直 BC 于点 D,且 AD=BC,BC 上方有一动点 P 满足 S△PBC=12S△ABC,则点 P 到 B,C 两点距离之和最小时,∠PBC 的度数为 ??
A. 30? B. 45? C. 60? D. 90?
(3分)如图,等腰三角形 ABC 的底边 BC 长为 4,面积是 16,腰 AC 的垂直平分线 EF 分别交 AC,AB 边于 E,F 点.若点 D 为 BC 边的中点,点 M 为线段 EF 上一动点,则 △CDM 周长的最小值为 ??
A. 6 B. 8 C. 10 D. 12
(3分)如图,正 △ABC 的边长为 2,过点 B 的直线 l⊥AB,且 △ABC 与 △A?BC? 关于直线 l 对称,D 为线段 BC? 上一动点,则 AD+CD 的最小值是 (??)
A. 3 B. 2 C. 32 D. 4
如图,在学习了轴对称后,小明在课外研究三角板时发现“两块完全相同的含有 30? 的三角板可以拼成一个等边三角形”,请你帮他解决以下问题:在直角 △ABC 中,∠ACB=90?,∠A=30?,AC=6,BC≈3.5,点 E,P 分别在斜边 AB 和直角边 AC 上,则 EP+BP 的最小值是 ??
A. 3.5 B. 4 C. 6 D. 9.5
(3分)如图,在直角坐标系中,点 A,B 的坐标分别为 1,4 和 3,0,点 C 是 y 轴上的一个动点,且 A,B,C 三点不在同一条直线上,当 △ABC 的周长最小时,点 C 的坐标是 ??
A. 0,0 B. 0,1 C. 0,2 D. 0,3
(3分)如图,在锐角三角形 ABC 中,AB=4,△ABC 的面积为 8,BD 平分 ∠ABC.若 M,N 分别是 BD,BC 上的动点,则 CM+MN 的最小值是 ??
A. 2 B. 4 C. 6 D. 8
二、填空题(24分)
(3分)如图,牧童在 A 处放牛,其家在 B 处,A,B 到河岸的距离分别为 AC 和 BD,且 AC=BD,若点 A 到河岸 CD 的中点的距离为 500 米,则牧童从 A 处把牛牵到河边饮水再回家,最短距离是 米.
(3分)如图,∠AOB=30?,点 P 是 ∠AOB 内任意一点,且 OP=7,点 E 和点 F 分别是射线 OA 和射线 OB 上的动点,则 △PEF 周长的最小值是 .
(3分)如图,一个旅游船从大桥 AB 的 P 处前往山脚下的 Q 处接游客,然后将游客送往河岸 BC 上,再回到 P 处,请画出旅游船的最短路径(实际行走路径画实线,其它辅助线画虚线) .
(3分)如图,若 ∠MON=42?,P 为 ∠MON 内一定点,OM 上有一个点 A,ON 上有一个点 B,当 △PAB 的周长取最小值时,则 ∠APB 的度数是 ?.
(3分)如图,在四边形 ABCD 中,∠A=∠C=90?,∠B=34?,在边 AB,BC 上分别找一点 E,F,使 △DEF 的周长最小,此时 ∠EDF= .
(3分)如图,在边长为 4 的正方形 ABCD 中,E 是 AB 边上的一点,且 AE=3,点 Q 为对角线 AC 上的动点,则 △BEQ 周长的最小值为 .
(3分)如图,在 Rt△ABC 中,∠C=90?,∠B=60?,点 D 在 BC 上且 BD=1,AD=4,点 E,F 分别为边 AC,AB 上的动点,△DEF 的周长的最小值为 .
(3分)如图,P 是 ∠AOB 内任意一点,OP=5?cm,M,N 分别是射线 OA 和 OB 上的动点,PN+PM+MN 的最小值是 5?cm,则 ∠AOB 的度数是 .
三、解答题(60分)
(10分)如图,已知 A,B 在直线 l 的同侧,在直线 l 上求一点 P,使 PA+PB 最小.
(10分)如图,在边长为 1 个单位长度的小正方形组成的正方形网格中,点 A,B,C 在小正方形的顶点上.
(1) 在图中画出与 △ABC 关于直线 l 成轴对称的 △A?B?C?;
(2) 线段 CC? 与直线 l 的位置关系是 ;
(3) △ABC 的面积为 ;
(4) 在直线 l 上找一点 P,使 PB+PC 的长最短(标出点 P).
(10分)如图,△ABC 在平面直角坐标系中,点 B 的坐标为 3,?5.
(1) 请在图中画出与 △ABC 关于 x 轴对称的 △A?B?C?,并写出点 A? 的坐标.
(2) 请在图中的 y 轴上画出一点 P,使得 △B?PC? 的周长最短.
(10分)如图所示,有两个村庄 A,B 在一公路 CD 的一侧,如果把 A,B 村庄的位置放在格点图中.
1 请作出 A 点关于 CD 的对称点 A?;
2 若要在公路 CD 上修建一个菜鸟驿站 P,使得驿站到两个村庄的线段距离和最小,请作出 P 点的位置.
(10分)请回答下列问题:
(1) 先化简,再求值:x?y2?yy+2x÷x,其中 ∣x?3∣+y+12=0.
(2) 如图,在单位长度为 1 的正方形网格中,点 A,B,C 都在格点上.
①填空:△ABC 的面积为 ;
②画出 △ABC 关于直线 l 对称的 △A?B?C?,其中点 A,B,C 的对应点分别为 A?,B?,C?;
③在直线 l 上画出一个点 P,使 PA+PC 的值最小.
(10分)如图,方格纸中每个小正方的边长均为 1?cm,四边形 ABCD 的四个顶点都在小正方形的顶点上,点 E 在 BC 边上,且点 E 在小正方形的顶点上,连接 AE.
(1) 在图中画出 △AEF,使 △AEF 与 △AEB 关于直线 AE 对称;
(2) 在图中 AE 上画出点 G,使 △CDG 周长最小;
(3) 连接 FG,请直接写出 △EFG 的面积 cm2.
答案
一、选择题(36分)
1. 【答案】D
【知识点】轴对称之最短路径
2. 【答案】B
【解析】 ∵AD 平分 ∠CAB,
∴ 点 B 关于 AD 的对称点 B? 在线段 AC 上,
作 B?N?⊥AB 于 N? 交 AD 于 M?.
∵BM+MN=B?M+MN,
∴ 当 M 与 M? 重合,N 与 N? 重合时,BM+MN 的值最小,最小值为 B?N?,
∵AD 垂直平分 BB?,
∵AB?=AB=52,
∵∠B?AN?=45?,
∴△AB?N? 是等腰直角三角形,
∴B?N?=5.
∴BM+MN 的最小值为 5.
【知识点】垂直平分线的性质、等腰直角三角形、轴对称之最短路径
3. 【答案】C
【解析】连接 BP,
∵△ABC 是等边三角形,D 是 BC 的中点,
∴AD 是 BC 的垂直平分线,
∴PB=PC,
当 PC+PE 的长最小时,即 PB+PE 最小,
则此时点 B,P,E 在同一直线上时,
又 ∵BE 为中线,
∴ 点 P 为 △ABC 的三条中线的交点,也就是 △ABC 的重心.
【知识点】等边三角形的性质、轴对称之最短路径、三角形的重心
4. 【答案】C
【解析】因为 P 与 P1 关于 OA 对称,
所以 OA 为 PP1 的垂直平分线,
所以 MP=MP1,
P 与 P2 关于 OB 对称,
所以 OB 为 PP2 的垂直平分线,
所以 NP=NP2,
于是 △PMN 周长为 MN+MP+NP=MN+MP1+NP2=P1P2=6.
【知识点】轴对称之最短路径
5. 【答案】C
【知识点】垂直平分线的性质、轴对称之最短路径
6. 【答案】D
【知识点】轴对称之最短路径
7. 【答案】B
【解析】 ∵S△PBC=12S△ABC,
∴P 在与 BC 平行,且到 BC 的距离为 12AD 的直线 l 上,
∴l∥BC,
作点 B 关于直线 l 的对称点 B?,连接 B?C 交 l 于 P,如图所示:
则 BB?⊥l,PB=PB?,此时点 P 到 B,C 两点距离之和最小,
作 PM⊥BC 于 M,则 BB?=2PM=AD,
∵AD⊥BC,AD=BC,
∴BB?=BC,BB?⊥BC,
∴△BB?C 是等腰直角三角形,
∴∠B?=45?,
∵PB=PB?,
∴∠PBB?=∠B?=45?,
∴∠PBC=90??45?=45?.
【知识点】轴对称之最短路径、等腰直角三角形
8. 【答案】C
【解析】连接 AM,
∵△ABC 是等腰三角形,点 D 是 BC 边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×4×AD=16,
解得 AD=8,
∵EF 是线段 AC 的垂直平分线,
∴ 点 C 关于直线 EF 的对称点为点 A,
∴AD 的长为 CM+MD 的最小值,
∴△CDM的周长最短=CM+MD+CD=AD+12BC=8+12×4=8+2=10.
故选C.
【知识点】轴对称之最短路径、等腰三角形的性质、垂直平分线的性质
9. 【答案】D
【解析】连接 CC?,如图所示:
∵△ABC,△A?BC? 均为正三角形,
∴∠ABC=∠A?=60?,A?B=BC=A?C?,
∴A?C?∥BC,
∴ 四边形 A?BCC? 为菱形,
∴ 点 C 关于 BC? 对称的点是 A?,即 CD=A?D,
∴ 当点 D 与点 B 重合时,AD+CD 取最小值,
此时 AD+CD=2+2=4.
【知识点】轴对称之最短路径
10. 【答案】C
【解析】作点 B 关于 AC 的对称点 B?,过 B? 作 B?E 上 AB 交 AC 于点 P,
则 EP+BP 的最小值为 B?E;
由题意可得两块完全相同的含有 30? 的三角板可以拼成一个等边三角形,
又 B?E⊥AB,AC⊥BB?,
故 B?E=AC=6.
【知识点】等边三角形的性质、轴对称之最短路径
11. 【答案】D
【解析】作 B 点关于 y 轴对称点 B? 点,连接 AB?,交 y 轴于点 C?,
此时 △ABC 的周长最小,
∵ 点 A,B 的坐标分别为 1,4 和 3,0,
∴B? 点坐标为:?3,0,AE=4,则 B?E=4,即 B?E=AE,
∵C?O∥AE,
∴B?O=C?O=3,
∴ 点 C? 的坐标是 0,3,此时 △ABC 的周长最小.
【知识点】轴对称之最短路径、平行线的性质
12. 【答案】B
【解析】过点 C 作 CE⊥AB 于点 E,交 BD 于点 M?,过点 M 作 MN?⊥BC 于 N?,
∵BD 平分 ∠ABC,M?E⊥AB 于点 E,M?N?⊥BC 于 N
∴M?N?=M?E,
∴CE=CM?+M?E
∴ 当点 M 与 M? 重合,点 N 与 N? 重合时,CM+MN 的最小值.
∵ 三角形 ABC 的面积为 8,AB=4,
∴12×4?CE=8,
∴CE=4.即 CM+MN 的最小值为 4.
【知识点】轴对称之最短路径、角平分线的性质
二、填空题(24分)
13. 【答案】 1000
【解析】作出 A 的对称点 A?,连接 A?B 与 CD 相交于 M,
则牧童从 A 处把牛牵到河边饮水再回家,最短距离是 A?B 的长.
易得 △A?CM≌△BDM,AC=BD,
∴A?C=BD,则 A?CBD=CMMD,
∴CM=DM,M 为 CD 的中点,
由于 A 到河岸 CD 的中点的距离为 500 米,
∴A? 到 M 的距离为 500 米,A?B=1000 米.
故最短距离是 1000 米.
【知识点】轴对称之最短路径、全等三角形的性质与判定
14. 【答案】 7
【解析】分别作点 P 关于 OA,OB 的对称点 C,D,
连接 CD,分别交 OA,OB 于点 E,F,
连接 OP,OC,OD,PE,PF,
∵ 点 P 关于 OA 的对称点为 C,
∴PE=CE,OP=OC,∠COA=∠POA,
∵ 点 P 关于 OB 的对称点为 D,
∴PF=DF,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=5cm,
∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2,
∠AOB=60?,
∴△COD 是等边三角形,
∴CD=OC=OD=5cm,
∴△PEF 的周长的最小值 =PE+EF+PF=CE+EF+DF≥CD=7.
【知识点】等边三角形的判定、轴对称之最短路径
15. 【答案】如图所示:
【解析】如图所示,作点 P 关于 BC 的对称点 P?,连接 P?Q 交 BC 于点 M,连接 MP.
最短路径为:P?Q?M?P.
【知识点】轴对称之最短路径
16. 【答案】 96
【解析】分别作点 P 关于 ON,OM 的对称点 P?,P?,
连接 OP?,OP?,P?P?,P?P? 交 OM,ON 于点 A,B,连接 PA,PB,
此时 △PAB 周长的最小值等于 P?P?.
由轴对称性质可得,OP?=OP?=OP,∠P?OA=∠POA,
∠P?OB=∠POB,
∴∠P?OP?=2∠MON=2×42?=84?,
∴∠OP?P?=∠OP?P?=180??84?÷2=48?,
又 ∵∠BPO=∠OP?B=48?,∠APO=∠AP?O=48?,
∴∠APB=∠APO+∠BPO=96?.
【知识点】轴对称之最短路径、轴对称的性质
17. 【答案】 112°
【解析】如图,作点 D 关于 BA 的对称点 P,点 D 关于 BC 的对称点 Q,连接 PQ,交 AB 于 E?,交 BC 于 F?,则点 E?,F? 即为所求.
∵ 四边形 ABCD 中,∠A=∠C=90?,∠B=α,
∴∠ADC=180??α,
由轴对称知,∠ADE?=∠P,∠CDF?=∠Q,
在 △PDQ 中,
∠P+∠Q=180??∠ADC=180??180??34?=34?,
∴∠ADE?+∠CDF?=∠P+∠Q=34?,
∴∠E?DF?=∠ADC?∠ADE?+∠CDF?=180??68?=112?.
【知识点】三角形的内角和、轴对称之最短路径
18. 【答案】 6
【解析】连接 BD,DE,
∵ 四边形 ABCD 是正方形,
∴ 点 B 与点 D 关于直线 AC 对称,
∴DE 的长即为 BQ+QE 的最小值,
∵DE=BQ+QE=AD2+AE2=42+32=5,
∴△BEQ周长的最小值=DE+BE=5+1=6.
故答案为 6.
【知识点】轴对称之最短路径
19. 【答案】 4
【解析】如图,作点 D 关于直线 AC 的对称点 D?,点 D 关于直线 AB 的对称点 D?,连接 D?D? 交 AC 于 E,交 AB 于 F,此时 △DEF 的周长最小,最小值为 D?D? 的长,连接 AD?,AD?,
在 Rt△ABC 中,∠C=90?,∠B=60?,
∴∠BAC=30?,
∵∠DAB=∠D?AB,∠DAC=D?AC,
∴∠D?AD?=2∠BAC=60?,
∴△AD?D? 是等边三角形,
∵AD?=AD=4,
∴D?D?=4,
∴△DEF 的周长的最小值为 4.
故答案为 4.
【知识点】等边三角形的判定、轴对称之最短路径
20. 【答案】 30?
【知识点】轴对称之最短路径、等边三角形的判定
三、解答题(60分)
21. 【答案】在直线 l 的另一侧找出点 A 的对称点 A?,连接 A?B 交 l 于 P 点即为所求.
【知识点】轴对称之最短路径
22. 【答案】
(1) 画图略.
(2) 直线 l 垂直平分线段 CC?
(3) 3
(4) 画图略.
【知识点】图形成轴对称、坐标平面内图形轴对称变换、坐标平面内图形的面积、轴对称之最短路径
23. 【答案】
(1) ?3,2,如图所示.
(2) 如图,点 P 即为所求.
【知识点】轴对称之最短路径、坐标平面内图形轴对称变换
24. 【答案】 1 如图所示:A? 点即为所求;
2 如图所示:点 P 即为所求.
【知识点】坐标平面内图形轴对称变换、轴对称之最短路径
25. 【答案】
(1) 原式=x2?2xy+y2?y2?2xy÷x=x2?4xy÷x=x?4y,
由 ∣x?3∣+y+12=0,
得到 x?3=0,y+1=0,
解得:x=3,y=?1,
则 原式=3+4=7.
(2) ① 2
②如图所示,即为所求;
③如图所示,即为所求.
【解析】
(2) ①根据题意得:S△ABC=12×2×2=2.
【知识点】轴对称图形、轴对称之最短路径、整式的加减乘除混合运算
26. 【答案】
(1) 如图 1 所示,
△AEF 即为所求.
(2) 如图 2 所示,作点 D 关于 AE 的对称点 D?,
连接 CD? 交 AE 于点 G,
∴DG=D?G,
此时 △CDG 的周长最小,
点 G 即为所求.
(3) 3
【解析】
(3) △EFG 的面积为 12×6×1=3cm2.
【知识点】画对称轴及轴对称图形、三角形的面积、轴对称之最短路径
