2021-2022学年人教版数学九年级上册24.1.4 圆周角 同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.1.4 圆周角 同步练习 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 698.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 00:00:00 | ||
图片预览





文档简介
24.1.4 圆周角
一、单选题
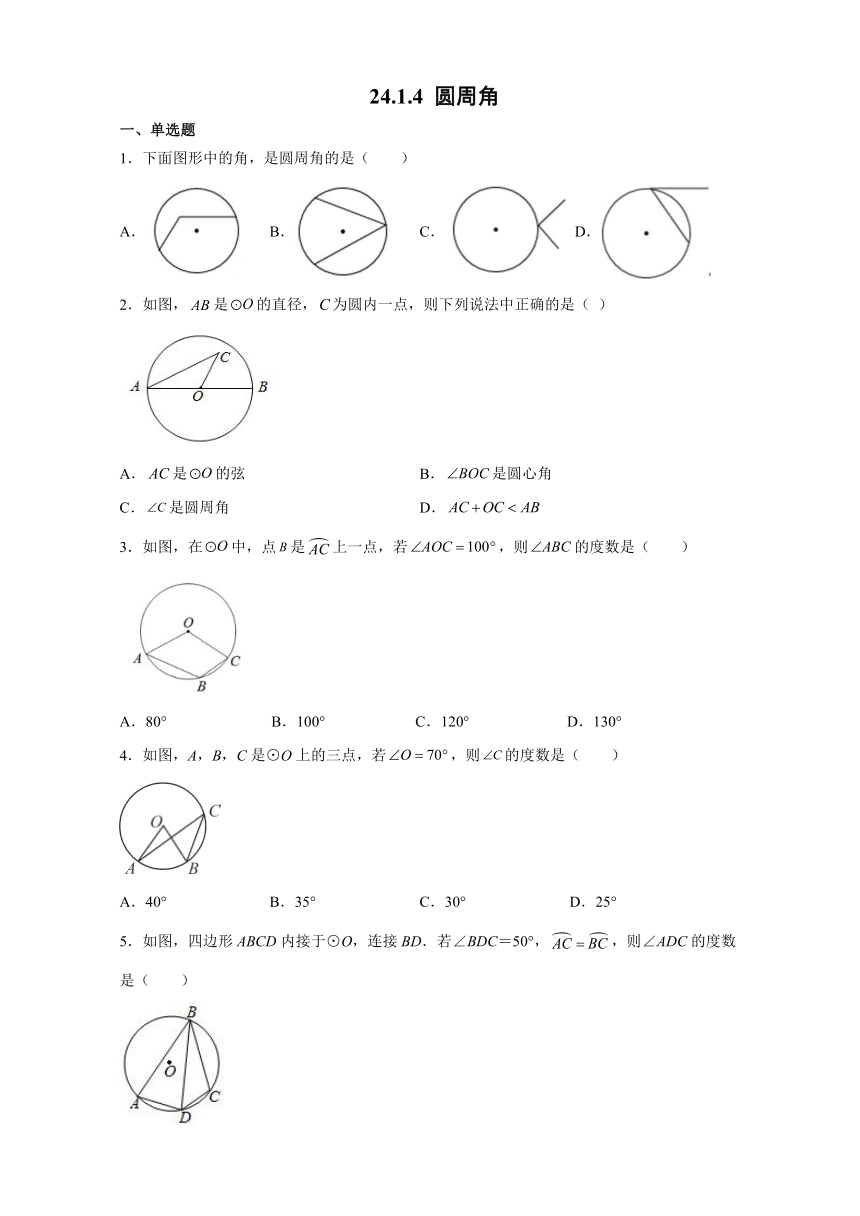
1.下面图形中的角,是圆周角的是( )
A. B. C. D.
2.如图,false是false的直径,false为圆内一点,则下列说法中正确的是( )
A.false是false的弦 B.false是圆心角
C.false是圆周角 D.false
3.如图,在false中,点false是false上一点,若false,则false的度数是( )
A.80° B.100° C.120° D.130°
4.如图,A,B,C是⊙O上的三点,若false,则false的度数是( )
A.40° B.35° C.30° D.25°
5.如图,四边形ABCD内接于⊙O,连接BD.若∠BDC=50°,false,则∠ADC的度数是( )
A.125° B.130° C.135° D.140°
6.如图,点A,B,C为⊙O上的三点,∠AOBfalse∠BOC,∠BAC=30°,则∠AOC的度数为( )
A.100° B.90° C.80° D.60°
7.如图,AB是⊙O的直径,点C、D都在⊙O上,若∠ABD=63°、∠DCO=24°,则∠BDC的度数是( )
A.15° B.24° C.39° D.63°
8.如图,false是⊙false的直径,点false在⊙false上,连接false,false,若false,则false( )
A.60° B.56° C.52° D.48°
9.如图,点false,false,false在false上,false,false,连接false交false于点false,则false的度数是( )
A.108° B.109° C.110° D.112°
10.如图,在Rt△ACB中,∠ACB=false,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
A.false B.false C.false D.5
11.如图,四边形false内接于false,点false为边false上任意一点(点false不与点false,false重合)连接false.若false,则false的度数可能为( )
A.false B.false C.false D.false
12.如图,false是半⊙false的直径,点false是弧false的中点,D为弧BC的中点,连接false,false于点false.则false( )
A.3 B.false C.false D.false
13.如图,false为false的直径,点C、D在false上,且false,false,则false的长为( )
A.false B.false C.false D.false
14.如图,四边形ABCD内接于⊙O,若∠BCD=105°,则∠BOD的度数为( )
A.40° B.70° C.150° D.140°
15.如图,AB是半圆O的直径,点C在半圆上,false,false,D是false上的一个动点,连接AD.过点C作false于E,连接BE,则BE的最小值是( )
A.false B.false C.false D.false
二、填空题
16.如图,四边形false内接于false,若它的一个外角false,则另一个外角false________false.
17.如图,false是false的直径,点false在false上,若false,则false_________°.
18.如图,劣弧false与false的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,求∠CAB的度数________.
19.图中圆心角false,点false是弧false的中点,则false__________.
20.如图,已知false是false的直径,且false,弦false,点false是弧false上的点,连接false、false,若false,则false的长为______.
三、解答题
21.如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交AC、BC于点D、E.
(1)求证:点E是BC的中点.
(2)若∠BOD=75°,求∠CED的度数.
22.如图,false是false的直径,false、false两点在false上,若false.
(1)求false的度数;
(2)若false,false,求false的半径.
23.如图,false为false的直径,false是false上的一点,连接false,false.false是false的中点,过false作false于点false,交false于点false.
(1)求证:false;
(2)若false,false,求false的长.
24.如图①,在⊙O中,弦CD垂直直径AB于点E.已知AC=4,BD=false.
(1)求直径AB的长.
(2)小慧说“若将题目条件中的‘直径AB’改为‘弦AB’,其余条件均不变(如图②),⊙O的直径仍不变”,你觉得小慧的说法正确吗?请说明理由.
25.如图,圆O中两条互相垂直的弦AB,CD交于点E.
(1)M是CD的中点,OM=3,CD=12,求圆O的半径长;
(2)点F在CD上,且CE=EF,求证:false.
参考答案
1.B
解:圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角,
观察四个选项可知,只有选项B中的角满足定义,
故选:B.
2.B
解:A、点C不在false上,所以AC不是false的弦,故错误,不符合题意;
B、因为点O是圆心,所以∠BOC是圆心角,故正确,符合题意;
C、点C不在false上,所以∠C不是圆周角,故错误,故不符合题意;
D、当点C在圆上时,则OC=OA=OB,若false成立,则AC+OC<OA+OB,
∴AC<OA,与题干矛盾,
∴D选项错误,不符合题意;
故选B.
3.D
解:在优弧AC上取点D,连接AD、CD,
∵∠AOC= 100° ,
∴∠ADC= false∠AOC=50° ,
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC= 180° ,
∴∠ABC= 180° -50° =130° ,
故选:D.
4.B
解:∵false,
∴false=falsefalse
故选B.
5.B
解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵false,
∴∠BOC=∠AOC=100°,
∴∠ABC=false∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
6.C
解:∵false对的圆心角为∠BOC,false对的圆周角为∠BAC,∠BAC=30°,
∴∠BOC=2∠CAB=60°,
∵∠AOBfalse∠BOC,
∴∠AOB=20°,
∴∠AOC=∠AOB +∠BOC=80°,
故选:C
7.C
解:连接AC,如图,
∵∠ACD=∠ABD=63°,∠DCO=24°,
∴∠ACO=∠ACD-∠DCO=63°-24°=39°,
∵OA=OC,
∴∠A=∠ACO=39°,
∴∠BDC=∠A=39°.
故选:C.
8.C
解:∵false是⊙false的直径,点false在⊙false上
∴OC=OA
∴∠BAC=∠OCA=26°
∴false2∠BAC=52°.
故选C.
9.B
解:如解图,连接false,false,
∵false,
∴false.
∵false,
∴false.
∵false,
∴false,
∴false,
∴false.
故选B.
10.C
解:在Rt△ACB中,false,
∵false为false的直径,
∴false,
∴false,
∴false,
故选C.
11.D
解:∵四边形false内接于false,
∴false,
∵false,
∴false,
∵false为false的外角,
∴false,只有D满足题意.
故选:D.
12.C
解:如图,连接false,BC、false.
∵false是直径,
∴false.
∵false,
∴false.
∴false.
∵false,
∴false.
∵false
∴false.
∵false,
∴false.
∴false.
∴false.
在false上取一点false,使得false,连接false.
设false,则false.
∵false,
∴false.
∴false.
∴false.
∴false.
故选:C
13.C
解:∵false为false的直径,false,
∴∠ACB=90°,false,
连接OD,
∵false,
∴∠DOB=60°,
∵OD=OB,
∴△OBD为等边三角形,
∴false,
故选:C.
14.C
解:∵四边形ABCD内接于⊙O,
∴∠A=180°﹣∠BCD=75°,
由圆周角定理得,∠BOD=2∠A=150°,
故选:C.
15.C
解:如图,取false的中点false,连接false,则false,
false,
false,
则在点false的移动过程中,点false在以false为半径的圆false上运动,
false是圆false的直径,
false,
在false中,false,
在false中,false,
由圆的性质得:当点false共线时,false取得最小值,最小值为false,
故选:C.
16.58
解:∵∠DCE=122°,
∴∠BCD=180°?122°=58°,
∴∠BAD=180°?58°=122°,
∴∠FAD=180°?122°=58°.
故答案为:58.
17.false
解:∵false,
∴false,
又∵AB是直径,
∴false,
∴false.
故答案为:false.
18.35°
解:由题意,弧BC与弧AD的度数之差为20°,
∴两弧所对圆心角相差20°,
∴2∠A-2∠C=20°,
∴∠A-∠C=10°…①;
∵∠CEB是△AEC的外角,
∴∠A+∠C=∠CEB=60°…②;
①+②,得:2∠A=70°,即∠A=35°.
故答案为:35°.
19.false
解:∵点B是弧AD的中点,
∴false,
∴∠AOB=∠BOD=30°,
∴∠AOD=60°
∵∠ACO=false∠AOD,
∴∠C=false×60°=30°.
故答案为30°.
20.9
解:连接OC和OE,如下图所示:
由同弧所对的圆周角等于圆心角的一半可知,∠A=false∠EOB,∠D=false∠COE,
∵∠A+∠D=30°,
∴false∠EOB+false∠COE=false∠COB=30°,
∴∠COB=60°,
∵CD⊥AB,
∴△COH为30°,60°,90°的三角形,其三边之比为false,
∴CH=false,
∴CD=2CH=9,
故答案为:9.
21.(1)见解析(2)37.5°.
(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
即点E为BC的中点;
(2)解:∵∠BOD=75°,
∴∠DAB=false∠BOD=37.5°,
∵∠DAB+∠DEB=180°,∠CED+∠DEB=180°,
∴∠CED=∠DAB=37.5°.
22.(1)false;(2)5.
解:(1)∵false,
∴false,
∵false是false的直径,
∴false,
∴false;
(2)连接false,
∵false是false直径,
∴false,
∵false,false,
∴false,
∴false的半径为5.
23.(1)见解析;(2)false的长度为false
(1)证明:延长false交false于点false.
∵false是直径,false,
∴点false是弧false的中点,false,
∵false是false的中点,
∴弧false弧false弧false,
∴弧false弧false,
∴false.
(2)连接false、false.
∵弧false弧false.
∴false
∴false.
在false中,false,
由(1)知,false,则false,
∵false,
∴OD=5,
在false中,false,
∴false,
设false,
在false中,
∵false,
∴false,
解得false,
即false的长度为false.
24.(1)false ;(2)(2)小慧的说法不正确,理由见解析
解:(1)连接AD,如图所示:
∵AB为直径,
∴∠ADB=90°,
∵弦CD垂直直径AB于点E,
∴由垂径定理可知:AD=AC=4,
在Rt△ADB中,AB=false=false;
(2)小慧的说法不正确,理由如下:因为若将题目条件中的“直径AB“改为“弦AB”,无法求出⊙O直径.
25.(1)false;(2)见解析.
(1)解:连接OC,
∵M是CD的中点,OM与圆O直径共线
∴false,false平分CD,
false
false
false.
在false中.
false
false
false
∴圆O的半径为false
(2)证明:连接AC,延长AF交BD于G.
false,false
false
又false
false
false
false
false
在false中
false
false
false
false
一、单选题
1.下面图形中的角,是圆周角的是( )
A. B. C. D.
2.如图,false是false的直径,false为圆内一点,则下列说法中正确的是( )
A.false是false的弦 B.false是圆心角
C.false是圆周角 D.false
3.如图,在false中,点false是false上一点,若false,则false的度数是( )
A.80° B.100° C.120° D.130°
4.如图,A,B,C是⊙O上的三点,若false,则false的度数是( )
A.40° B.35° C.30° D.25°
5.如图,四边形ABCD内接于⊙O,连接BD.若∠BDC=50°,false,则∠ADC的度数是( )
A.125° B.130° C.135° D.140°
6.如图,点A,B,C为⊙O上的三点,∠AOBfalse∠BOC,∠BAC=30°,则∠AOC的度数为( )
A.100° B.90° C.80° D.60°
7.如图,AB是⊙O的直径,点C、D都在⊙O上,若∠ABD=63°、∠DCO=24°,则∠BDC的度数是( )
A.15° B.24° C.39° D.63°
8.如图,false是⊙false的直径,点false在⊙false上,连接false,false,若false,则false( )
A.60° B.56° C.52° D.48°
9.如图,点false,false,false在false上,false,false,连接false交false于点false,则false的度数是( )
A.108° B.109° C.110° D.112°
10.如图,在Rt△ACB中,∠ACB=false,AC=6,BC=8,若以AC为直径的☉O交AB于点D,则CD的长为( )
A.false B.false C.false D.5
11.如图,四边形false内接于false,点false为边false上任意一点(点false不与点false,false重合)连接false.若false,则false的度数可能为( )
A.false B.false C.false D.false
12.如图,false是半⊙false的直径,点false是弧false的中点,D为弧BC的中点,连接false,false于点false.则false( )
A.3 B.false C.false D.false
13.如图,false为false的直径,点C、D在false上,且false,false,则false的长为( )
A.false B.false C.false D.false
14.如图,四边形ABCD内接于⊙O,若∠BCD=105°,则∠BOD的度数为( )
A.40° B.70° C.150° D.140°
15.如图,AB是半圆O的直径,点C在半圆上,false,false,D是false上的一个动点,连接AD.过点C作false于E,连接BE,则BE的最小值是( )
A.false B.false C.false D.false
二、填空题
16.如图,四边形false内接于false,若它的一个外角false,则另一个外角false________false.
17.如图,false是false的直径,点false在false上,若false,则false_________°.
18.如图,劣弧false与false的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,求∠CAB的度数________.
19.图中圆心角false,点false是弧false的中点,则false__________.
20.如图,已知false是false的直径,且false,弦false,点false是弧false上的点,连接false、false,若false,则false的长为______.
三、解答题
21.如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交AC、BC于点D、E.
(1)求证:点E是BC的中点.
(2)若∠BOD=75°,求∠CED的度数.
22.如图,false是false的直径,false、false两点在false上,若false.
(1)求false的度数;
(2)若false,false,求false的半径.
23.如图,false为false的直径,false是false上的一点,连接false,false.false是false的中点,过false作false于点false,交false于点false.
(1)求证:false;
(2)若false,false,求false的长.
24.如图①,在⊙O中,弦CD垂直直径AB于点E.已知AC=4,BD=false.
(1)求直径AB的长.
(2)小慧说“若将题目条件中的‘直径AB’改为‘弦AB’,其余条件均不变(如图②),⊙O的直径仍不变”,你觉得小慧的说法正确吗?请说明理由.
25.如图,圆O中两条互相垂直的弦AB,CD交于点E.
(1)M是CD的中点,OM=3,CD=12,求圆O的半径长;
(2)点F在CD上,且CE=EF,求证:false.
参考答案
1.B
解:圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角,
观察四个选项可知,只有选项B中的角满足定义,
故选:B.
2.B
解:A、点C不在false上,所以AC不是false的弦,故错误,不符合题意;
B、因为点O是圆心,所以∠BOC是圆心角,故正确,符合题意;
C、点C不在false上,所以∠C不是圆周角,故错误,故不符合题意;
D、当点C在圆上时,则OC=OA=OB,若false成立,则AC+OC<OA+OB,
∴AC<OA,与题干矛盾,
∴D选项错误,不符合题意;
故选B.
3.D
解:在优弧AC上取点D,连接AD、CD,
∵∠AOC= 100° ,
∴∠ADC= false∠AOC=50° ,
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC= 180° ,
∴∠ABC= 180° -50° =130° ,
故选:D.
4.B
解:∵false,
∴false=falsefalse
故选B.
5.B
解:连接OA,OB,OC,
∵∠BDC=50°,
∴∠BOC=2∠BDC=100°,
∵false,
∴∠BOC=∠AOC=100°,
∴∠ABC=false∠AOC=50°,
∴∠ADC=180°﹣∠ABC=130°.
故选:B.
6.C
解:∵false对的圆心角为∠BOC,false对的圆周角为∠BAC,∠BAC=30°,
∴∠BOC=2∠CAB=60°,
∵∠AOBfalse∠BOC,
∴∠AOB=20°,
∴∠AOC=∠AOB +∠BOC=80°,
故选:C
7.C
解:连接AC,如图,
∵∠ACD=∠ABD=63°,∠DCO=24°,
∴∠ACO=∠ACD-∠DCO=63°-24°=39°,
∵OA=OC,
∴∠A=∠ACO=39°,
∴∠BDC=∠A=39°.
故选:C.
8.C
解:∵false是⊙false的直径,点false在⊙false上
∴OC=OA
∴∠BAC=∠OCA=26°
∴false2∠BAC=52°.
故选C.
9.B
解:如解图,连接false,false,
∵false,
∴false.
∵false,
∴false.
∵false,
∴false,
∴false,
∴false.
故选B.
10.C
解:在Rt△ACB中,false,
∵false为false的直径,
∴false,
∴false,
∴false,
故选C.
11.D
解:∵四边形false内接于false,
∴false,
∵false,
∴false,
∵false为false的外角,
∴false,只有D满足题意.
故选:D.
12.C
解:如图,连接false,BC、false.
∵false是直径,
∴false.
∵false,
∴false.
∴false.
∵false,
∴false.
∵false
∴false.
∵false,
∴false.
∴false.
∴false.
在false上取一点false,使得false,连接false.
设false,则false.
∵false,
∴false.
∴false.
∴false.
∴false.
故选:C
13.C
解:∵false为false的直径,false,
∴∠ACB=90°,false,
连接OD,
∵false,
∴∠DOB=60°,
∵OD=OB,
∴△OBD为等边三角形,
∴false,
故选:C.
14.C
解:∵四边形ABCD内接于⊙O,
∴∠A=180°﹣∠BCD=75°,
由圆周角定理得,∠BOD=2∠A=150°,
故选:C.
15.C
解:如图,取false的中点false,连接false,则false,
false,
false,
则在点false的移动过程中,点false在以false为半径的圆false上运动,
false是圆false的直径,
false,
在false中,false,
在false中,false,
由圆的性质得:当点false共线时,false取得最小值,最小值为false,
故选:C.
16.58
解:∵∠DCE=122°,
∴∠BCD=180°?122°=58°,
∴∠BAD=180°?58°=122°,
∴∠FAD=180°?122°=58°.
故答案为:58.
17.false
解:∵false,
∴false,
又∵AB是直径,
∴false,
∴false.
故答案为:false.
18.35°
解:由题意,弧BC与弧AD的度数之差为20°,
∴两弧所对圆心角相差20°,
∴2∠A-2∠C=20°,
∴∠A-∠C=10°…①;
∵∠CEB是△AEC的外角,
∴∠A+∠C=∠CEB=60°…②;
①+②,得:2∠A=70°,即∠A=35°.
故答案为:35°.
19.false
解:∵点B是弧AD的中点,
∴false,
∴∠AOB=∠BOD=30°,
∴∠AOD=60°
∵∠ACO=false∠AOD,
∴∠C=false×60°=30°.
故答案为30°.
20.9
解:连接OC和OE,如下图所示:
由同弧所对的圆周角等于圆心角的一半可知,∠A=false∠EOB,∠D=false∠COE,
∵∠A+∠D=30°,
∴false∠EOB+false∠COE=false∠COB=30°,
∴∠COB=60°,
∵CD⊥AB,
∴△COH为30°,60°,90°的三角形,其三边之比为false,
∴CH=false,
∴CD=2CH=9,
故答案为:9.
21.(1)见解析(2)37.5°.
(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
即点E为BC的中点;
(2)解:∵∠BOD=75°,
∴∠DAB=false∠BOD=37.5°,
∵∠DAB+∠DEB=180°,∠CED+∠DEB=180°,
∴∠CED=∠DAB=37.5°.
22.(1)false;(2)5.
解:(1)∵false,
∴false,
∵false是false的直径,
∴false,
∴false;
(2)连接false,
∵false是false直径,
∴false,
∵false,false,
∴false,
∴false的半径为5.
23.(1)见解析;(2)false的长度为false
(1)证明:延长false交false于点false.
∵false是直径,false,
∴点false是弧false的中点,false,
∵false是false的中点,
∴弧false弧false弧false,
∴弧false弧false,
∴false.
(2)连接false、false.
∵弧false弧false.
∴false
∴false.
在false中,false,
由(1)知,false,则false,
∵false,
∴OD=5,
在false中,false,
∴false,
设false,
在false中,
∵false,
∴false,
解得false,
即false的长度为false.
24.(1)false ;(2)(2)小慧的说法不正确,理由见解析
解:(1)连接AD,如图所示:
∵AB为直径,
∴∠ADB=90°,
∵弦CD垂直直径AB于点E,
∴由垂径定理可知:AD=AC=4,
在Rt△ADB中,AB=false=false;
(2)小慧的说法不正确,理由如下:因为若将题目条件中的“直径AB“改为“弦AB”,无法求出⊙O直径.
25.(1)false;(2)见解析.
(1)解:连接OC,
∵M是CD的中点,OM与圆O直径共线
∴false,false平分CD,
false
false
false.
在false中.
false
false
false
∴圆O的半径为false
(2)证明:连接AC,延长AF交BD于G.
false,false
false
又false
false
false
false
false
在false中
false
false
false
false
同课章节目录
