3.3.2指数函数的图像和性质(第一课时)课件(共43张PPT )——2021-2022学年高一上学期数学北师大版(2019)必修第一册
文档属性
| 名称 | 3.3.2指数函数的图像和性质(第一课时)课件(共43张PPT )——2021-2022学年高一上学期数学北师大版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 09:55:41 | ||
图片预览






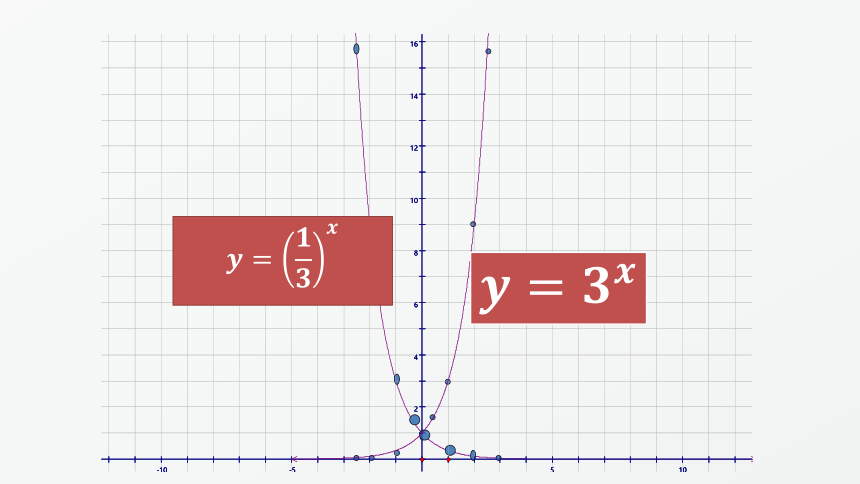


文档简介
3.3.2指数函数的图像和性质
第一课时
教学目标
01
03
会画指数函数的图象,并利用图象解题.
掌握指数函数的图象和性质.
01
了解指数函数的图象的变换
指数函数的图像和性质
重点
难点
指数函数图像对性质的影响.
环节一
指数函数图像
1.在同一坐标系中分别作出如下函数的图像
特殊指数图像
????=????????
?
????=????????????
?
列表如下
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
????=????????????
?
????=????????
?
2.在同一坐标系中分别作出如下函数的图像
特殊指数图像
????=????????
?
????=????????????
?
列表如下
x
…
-2.5
-2
-1
-0.5
0
0.5
1
2
2.5
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
15.6
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
0.06
…
( )
????=????????
?
????=????????????
?
归纳指数图像
通过作图,我们发现y=ax的图象大致分两种类型,即0<a<1和a>1,图象如下:
x
y
(0,1)
y = 1
y = a x
(a> 1)
0
x
y
y = 1
y =a x
(0<a <1)
(0,1)
0
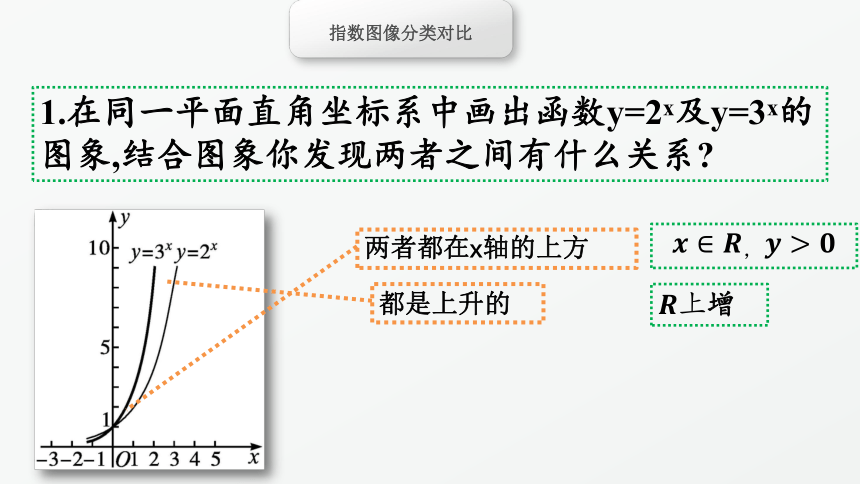
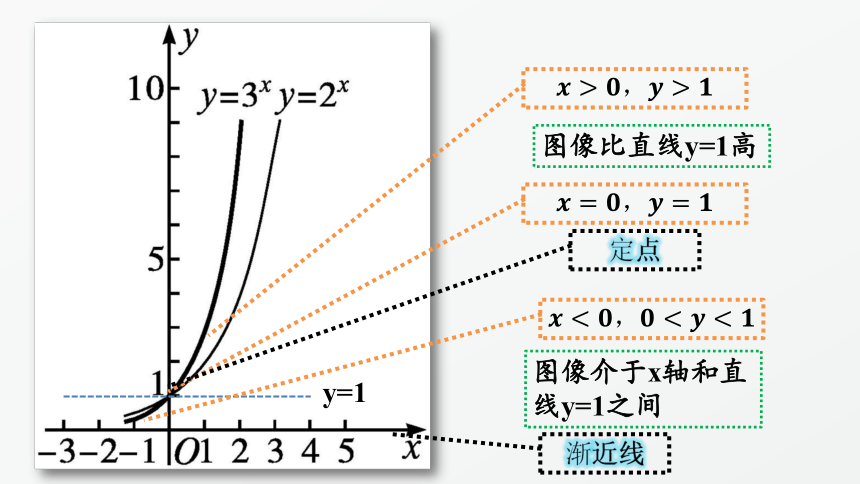
1.在同一平面直角坐标系中画出函数y=2x及y=3x的图象,结合图象你发现两者之间有什么关系?
两者都在x轴的上方
都是上升的
指数图像分类对比
????∈????,????>????
?
????上增
?
y=1
????>????,????>????
?
????=????,????=????
?
?????
图像比直线y=1高
图像介于x轴和直线y=1之间
定点
?
渐近线
?
指数图像和性质归纳
(1)一般地,当a>1时,指数函数y=ax的定义域是R,值域是(0,+∞),过定点(0,1),在R上是增函数.当x值趋近于正无穷大时,函数值趋近于 正无穷大;当x值趋近于负无穷大时,函数值趋近于0.
(2)对于函数y=ax和y=bx(a>b>1):
①当x<0时,0②当x=0时,ax=bx=1;
③当x>0时,ax>bx>1.
指数图像分类对比
2.在同一平面直角坐标系中画出函数y=????????????及y=????????????的图象,结合图象你发现两者之间有什么关系?
?
两者都在x轴的上方
两者都下降
????∈????,????>????
?
????上减
?
y=1
????>????,?????
图像介于x轴和直线y=1之间
????=????,?????=????
?
定点
?
????????
?
图像比直线y=1高
渐近线
?
(3)一般地,当0(4)对于函数y=ax和y=bx(0①当x<0时,ax>bx>1;
②当x=0时,ax=bx=1;
③当x>0时,0指数图像和性质归纳
指数函数图像与性质汇综
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}指数函数
指数函数
定义
y=ax(a>0,a≠1,x∈R)
图像
性质
(1)定义域:________.
(2)值域:________.
(3)过点________.
(4)当a>1时,在R上是________函数;
当0R
0,+∞
?
0,1
?
增
?
减
?
微练
y=????????????的图象可能是( )
?
解析 0<<1且过点(0,1),故选C.
环节二
指数函数图像拓展
1.底数对指数函数图像变化的影响
例1.如图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.aB.bC.1D.a解析:方法1:在y轴的右侧,指数函数的图象由下到上,底数依次增大.由指数函数图象的升降,知c>d>1,0∴b方法2:如图,作直线x=1,与四个函数的
图象分别交于A,B,C,D四点,将x=1代入
各个函数可得函数值等于底数,所以四
个交点的纵坐标越大,则底数越大,由图
可知b经验一
无论指数函数的底数a如何变化,指数函数y=ax(a>0,且a≠1)的图象与直线x=1相交于点(1,a),由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.
微练
如图,若0解析:因为0答案:D
例2.已知函数y=ax+b的图像经过第一、三、四象限,试确定a,b的取值范围.
2.指数函数图像的平移变换
[分析] 函数y=ax+b的图像是由y=ax的图像向上(b>0)或向下(b<0)平移|b|个单位得到的,其形状与y=ax的图像相同.
[解析] 如图所示,当x=0时,y<0,
∴a0+b<0,∴b<-1,显然a>1.
故a∈(1,+∞),b∈(-∞,-1).
经验二
1.利用熟悉的函数图像作图,再利用图像的平移、对称等变换,平移需分清向哪个方向移,再移多少个单位.口诀是【左加右减】【加上减下】
2.左右平移不改变原来的【渐近线】,上下平移图像,渐近线也同步平移。
3.指数函数图像的翻折变换
例3.函数y=|2x-2|的图象是( )
解析 (1)y=2x-2的图象是由y=2x的图象向下平移2个单位长度得到的,故y=|2x-2|的图象是由y=2x-2的图象在x轴上方的部分不变,下方部分对折到x轴的上方得到的.
外加绝对值,下翻上
3.指数函数图像的翻折变换
例4.直线y=2a与函数y=|ax-1|(a>0且a≠1)的图象有两个公共点,则a的取值范围是________.
解:当a>1时,在同一坐标系中作出函数y=2a和y=|ax-1|的图象(如图(1))
由图象可知两函数图象只能有一个公共点,此时无解.
当0<a<1,作出函数y=2a和y=|ax-1|的图象(如图(2)).
若直线y=2a与函数y=|ax-1|(a>0且a≠1)的图象有两个交点,由图象可知0<2a<1,所以0<a<????????.
?
函数y=????????????的图像大致是( )
?
微练
A
B
C
D
解析:先画????=????????????图像,留下y轴右侧的图像,并把它翻折到左边,选B.
?
内绝对值,右翻左
经验三
先画指数函数y=axa>0,a≠1的基本图像
1.y=ax+b,可由y=ax的图像平移为y=ax+b,然后,【下翻上】;
2.????=????????的图像,可由y=ax的图像,【右翻左】
3.注意变化过程中,图像渐近线的变化。
?
4.指数函数图像的对称变换
例5.函数y=23-x与________的图象关于y轴对称,与________的图象关于x轴对称,与________的图象关于原点对称.
解:因为图象与y=2-x关于y轴对称的函数为y=2x,所以函数y=23-x与y=23+x的图象关于y轴对称.关于x轴对称的图象为y=-23-x,关于原点对称的图象为y=-23+x.
经验四
??????已知y=fx的图像
1.关于x轴对称的图像对应的函数是y=?fx;
2.关于y轴对称的图像对应的函数是y=f?x;
3.关于原点对称的图像对应的函数是y=?f?x;
?
环节三
利用图像研究性质
1.单调性
例6.求下列函数的增区间
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解:(1)????????=?????????????的图像可由????=????????的图像向右平移3个单位得到。如图,函数增区间是R;
?
1.单调性
例6.求下列函数的增区间
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解:(2)????????=?????????????的图像可由????=????????的图像通过【右翻左】得到????=????????,再向下平移1个单位得到。如图,函数增区间是????,+∞;
?
1.单调性
例6.求下列函数的增区间
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解:(3)分段函数,由两部分组合而成。如图,增区间是R
?
1.单调性
例7.若函数f(x)=????????,????>1,4?????2????+2,????≤1是R上的增函数,则实数a的取值范围为( )
A.(1,+∞) B.(1,8) C.(4,8) D.[4,8)
?
分析
以前讲过,分段函数在R上增,需要每段都增,且后段图像不低于前段图像。
解析:4?????2>0????>1????≥6?????2解此不等式组,得a∈[4,8).
?
2.值域
例8.求下列函数在?????,????上值域
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解(1)如图,值域是????????????,????????
?
-1
2
解(2)如图,值域是????,????
?
解(3)如图,值域是????,????
?
-1
2
3.比大小
例9.比较下列各组数的大小:
(1)1.70.3,1.50.3;(2)1.70.3,0.83.1.
解:
1.70.3
1.50.3
3.比大小
例9.比较下列各组数的大小:
(1)1.70.3,1.50.3;(2)1.70.3,0.83.1.
解:
1.70.3
0.83.1
例10.已知函数f(x)=12|????|,设a=f(20.3),b=f(0.32),c=f(1),则a,b,c的大小关系是( )
A.b>c>a B.b>a>c C.c>a>b D.a>b>c
?
3.比大小
解析:如图可知,选A
4.解不等式
例11.若已知函数f(x)=1????,????<0,13????,????≥0,则不等式|f(x)|≥13的解集为 .?
?
解析:画出分段函数图像后,【下翻上】,然后,画直线????=????????,取适合的部分,写出对应的解集
?
????=????????
?
????=????????
?
|????(????)|≥13解集 {x|-3≤x≤1}.
?
课堂小结
1.核心要点
1.指数函数图像;基本图像+变换
2.利用图像解决指数函数部分性质
2.数学素养
体会数学抽象的过程,强化直观想象素养的培养.
谢谢观看
课件制作老师:胡琪
第一课时
教学目标
01
03
会画指数函数的图象,并利用图象解题.
掌握指数函数的图象和性质.
01
了解指数函数的图象的变换
指数函数的图像和性质
重点
难点
指数函数图像对性质的影响.
环节一
指数函数图像
1.在同一坐标系中分别作出如下函数的图像
特殊指数图像
????=????????
?
????=????????????
?
列表如下
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
x
…
-3
-2
-1
-0.5
0
0.5
1
2
3
…
…
0.13
0.25
0.5
0.71
1
1.4
2
4
8
…
…
8
4
2
1.4
1
0.71
0.5
0.25
0.13
…
????=????????????
?
????=????????
?
2.在同一坐标系中分别作出如下函数的图像
特殊指数图像
????=????????
?
????=????????????
?
列表如下
x
…
-2.5
-2
-1
-0.5
0
0.5
1
2
2.5
…
…
0.06
0.1
0.3
0.6
1
1.7
3
9
15.6
…
…
15.6
9
3
1.7
1
0.6
0.3
0.1
0.06
…
( )
????=????????
?
????=????????????
?
归纳指数图像
通过作图,我们发现y=ax的图象大致分两种类型,即0<a<1和a>1,图象如下:
x
y
(0,1)
y = 1
y = a x
(a> 1)
0
x
y
y = 1
y =a x
(0<a <1)
(0,1)
0
1.在同一平面直角坐标系中画出函数y=2x及y=3x的图象,结合图象你发现两者之间有什么关系?
两者都在x轴的上方
都是上升的
指数图像分类对比
????∈????,????>????
?
????上增
?
y=1
????>????,????>????
?
????=????,????=????
?
?????
图像比直线y=1高
图像介于x轴和直线y=1之间
定点
?
渐近线
?
指数图像和性质归纳
(1)一般地,当a>1时,指数函数y=ax的定义域是R,值域是(0,+∞),过定点(0,1),在R上是增函数.当x值趋近于正无穷大时,函数值趋近于 正无穷大;当x值趋近于负无穷大时,函数值趋近于0.
(2)对于函数y=ax和y=bx(a>b>1):
①当x<0时,0
③当x>0时,ax>bx>1.
指数图像分类对比
2.在同一平面直角坐标系中画出函数y=????????????及y=????????????的图象,结合图象你发现两者之间有什么关系?
?
两者都在x轴的上方
两者都下降
????∈????,????>????
?
????上减
?
y=1
????>????,?????
图像介于x轴和直线y=1之间
????=????,?????=????
?
定点
?
????????
?
图像比直线y=1高
渐近线
?
(3)一般地,当0
②当x=0时,ax=bx=1;
③当x>0时,0
指数函数图像与性质汇综
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}指数函数
指数函数
定义
y=ax(a>0,a≠1,x∈R)
图像
性质
(1)定义域:________.
(2)值域:________.
(3)过点________.
(4)当a>1时,在R上是________函数;
当0
0,+∞
?
0,1
?
增
?
减
?
微练
y=????????????的图象可能是( )
?
解析 0<<1且过点(0,1),故选C.
环节二
指数函数图像拓展
1.底数对指数函数图像变化的影响
例1.如图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.a
图象分别交于A,B,C,D四点,将x=1代入
各个函数可得函数值等于底数,所以四
个交点的纵坐标越大,则底数越大,由图
可知b
无论指数函数的底数a如何变化,指数函数y=ax(a>0,且a≠1)的图象与直线x=1相交于点(1,a),由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.
微练
如图,若0
例2.已知函数y=ax+b的图像经过第一、三、四象限,试确定a,b的取值范围.
2.指数函数图像的平移变换
[分析] 函数y=ax+b的图像是由y=ax的图像向上(b>0)或向下(b<0)平移|b|个单位得到的,其形状与y=ax的图像相同.
[解析] 如图所示,当x=0时,y<0,
∴a0+b<0,∴b<-1,显然a>1.
故a∈(1,+∞),b∈(-∞,-1).
经验二
1.利用熟悉的函数图像作图,再利用图像的平移、对称等变换,平移需分清向哪个方向移,再移多少个单位.口诀是【左加右减】【加上减下】
2.左右平移不改变原来的【渐近线】,上下平移图像,渐近线也同步平移。
3.指数函数图像的翻折变换
例3.函数y=|2x-2|的图象是( )
解析 (1)y=2x-2的图象是由y=2x的图象向下平移2个单位长度得到的,故y=|2x-2|的图象是由y=2x-2的图象在x轴上方的部分不变,下方部分对折到x轴的上方得到的.
外加绝对值,下翻上
3.指数函数图像的翻折变换
例4.直线y=2a与函数y=|ax-1|(a>0且a≠1)的图象有两个公共点,则a的取值范围是________.
解:当a>1时,在同一坐标系中作出函数y=2a和y=|ax-1|的图象(如图(1))
由图象可知两函数图象只能有一个公共点,此时无解.
当0<a<1,作出函数y=2a和y=|ax-1|的图象(如图(2)).
若直线y=2a与函数y=|ax-1|(a>0且a≠1)的图象有两个交点,由图象可知0<2a<1,所以0<a<????????.
?
函数y=????????????的图像大致是( )
?
微练
A
B
C
D
解析:先画????=????????????图像,留下y轴右侧的图像,并把它翻折到左边,选B.
?
内绝对值,右翻左
经验三
先画指数函数y=axa>0,a≠1的基本图像
1.y=ax+b,可由y=ax的图像平移为y=ax+b,然后,【下翻上】;
2.????=????????的图像,可由y=ax的图像,【右翻左】
3.注意变化过程中,图像渐近线的变化。
?
4.指数函数图像的对称变换
例5.函数y=23-x与________的图象关于y轴对称,与________的图象关于x轴对称,与________的图象关于原点对称.
解:因为图象与y=2-x关于y轴对称的函数为y=2x,所以函数y=23-x与y=23+x的图象关于y轴对称.关于x轴对称的图象为y=-23-x,关于原点对称的图象为y=-23+x.
经验四
??????已知y=fx的图像
1.关于x轴对称的图像对应的函数是y=?fx;
2.关于y轴对称的图像对应的函数是y=f?x;
3.关于原点对称的图像对应的函数是y=?f?x;
?
环节三
利用图像研究性质
1.单调性
例6.求下列函数的增区间
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解:(1)????????=?????????????的图像可由????=????????的图像向右平移3个单位得到。如图,函数增区间是R;
?
1.单调性
例6.求下列函数的增区间
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解:(2)????????=?????????????的图像可由????=????????的图像通过【右翻左】得到????=????????,再向下平移1个单位得到。如图,函数增区间是????,+∞;
?
1.单调性
例6.求下列函数的增区间
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解:(3)分段函数,由两部分组合而成。如图,增区间是R
?
1.单调性
例7.若函数f(x)=????????,????>1,4?????2????+2,????≤1是R上的增函数,则实数a的取值范围为( )
A.(1,+∞) B.(1,8) C.(4,8) D.[4,8)
?
分析
以前讲过,分段函数在R上增,需要每段都增,且后段图像不低于前段图像。
解析:4?????2>0????>1????≥6?????2解此不等式组,得a∈[4,8).
?
2.值域
例8.求下列函数在?????,????上值域
(1)函数????????=?????????????;
(2)函数????????=?????????????;
(3)函数????????=????+????,????≤.????????????,????>????
?
解(1)如图,值域是????????????,????????
?
-1
2
解(2)如图,值域是????,????
?
解(3)如图,值域是????,????
?
-1
2
3.比大小
例9.比较下列各组数的大小:
(1)1.70.3,1.50.3;(2)1.70.3,0.83.1.
解:
1.70.3
1.50.3
3.比大小
例9.比较下列各组数的大小:
(1)1.70.3,1.50.3;(2)1.70.3,0.83.1.
解:
1.70.3
0.83.1
例10.已知函数f(x)=12|????|,设a=f(20.3),b=f(0.32),c=f(1),则a,b,c的大小关系是( )
A.b>c>a B.b>a>c C.c>a>b D.a>b>c
?
3.比大小
解析:如图可知,选A
4.解不等式
例11.若已知函数f(x)=1????,????<0,13????,????≥0,则不等式|f(x)|≥13的解集为 .?
?
解析:画出分段函数图像后,【下翻上】,然后,画直线????=????????,取适合的部分,写出对应的解集
?
????=????????
?
????=????????
?
|????(????)|≥13解集 {x|-3≤x≤1}.
?
课堂小结
1.核心要点
1.指数函数图像;基本图像+变换
2.利用图像解决指数函数部分性质
2.数学素养
体会数学抽象的过程,强化直观想象素养的培养.
谢谢观看
课件制作老师:胡琪
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
