2020-2021学年安徽省马鞍山市和县七年级(下)期末数学试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年安徽省马鞍山市和县七年级(下)期末数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 784.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 07:08:28 | ||
图片预览



文档简介
2020-2021学年安徽省马鞍山市和县七年级(下)期末数学试卷
一、选择题(共10个小题,每小题4分).
1.计算的平方根为( )
A.±4 B.±2 C.4 D.±
2.下列调查中:①了解某班学生学习中国共产党党史的情况;②选出某校1000米跑的最快的学生;③了解全国中学生视力情况;④了解长江中鱼的种类.适合采取抽样调查的是( )
A.①③ B.②④ C.①② D.③④
3.为了迎接端午节,某校食堂推出四种粽子新款(分别以A,B,C,D表示),请学生代表免费试吃选出最喜欢的品种,结果反馈如下:
CDDBABABBBACCBABABCDCD
通过以上数据,你能获得的信息是( )
A.A款粽子最受欢迎
B.B款粽子最受欢迎
C.喜欢C、D两款粽子的人加起来占样本的一半
D.D款粽子受欢迎程度仅次于C款
4.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
A.10° B.20° C.30° D.40°
5.已知a<b,则下列各式不成立的是( )
A.a﹣2<b﹣2 B.3a+b<4b C.1﹣2a<1﹣2b D.ac<bc(c>0)
6.关于x的一元一次方程x+m﹣2=0的解是负数,则m的取值范围是( )
A.m>2 B.m<2 C.m>﹣2 D.m<﹣2
7.打折前购买A商品40件与购买B商品30件所花的钱一样多,商家打折促销,A商品打八折,B商品打九折,此时购买A商品40件比购买B商品30件少花600元,则打折前A商品和B商品每件的价格分别为( )
A.75元,100元 B.120元,160元
C.150元,200元 D.180元,240元
8.已知是关于x、y的二元一次方程组的解,则2m﹣n的立方根是( )
A.1 B.±1 C. D.±
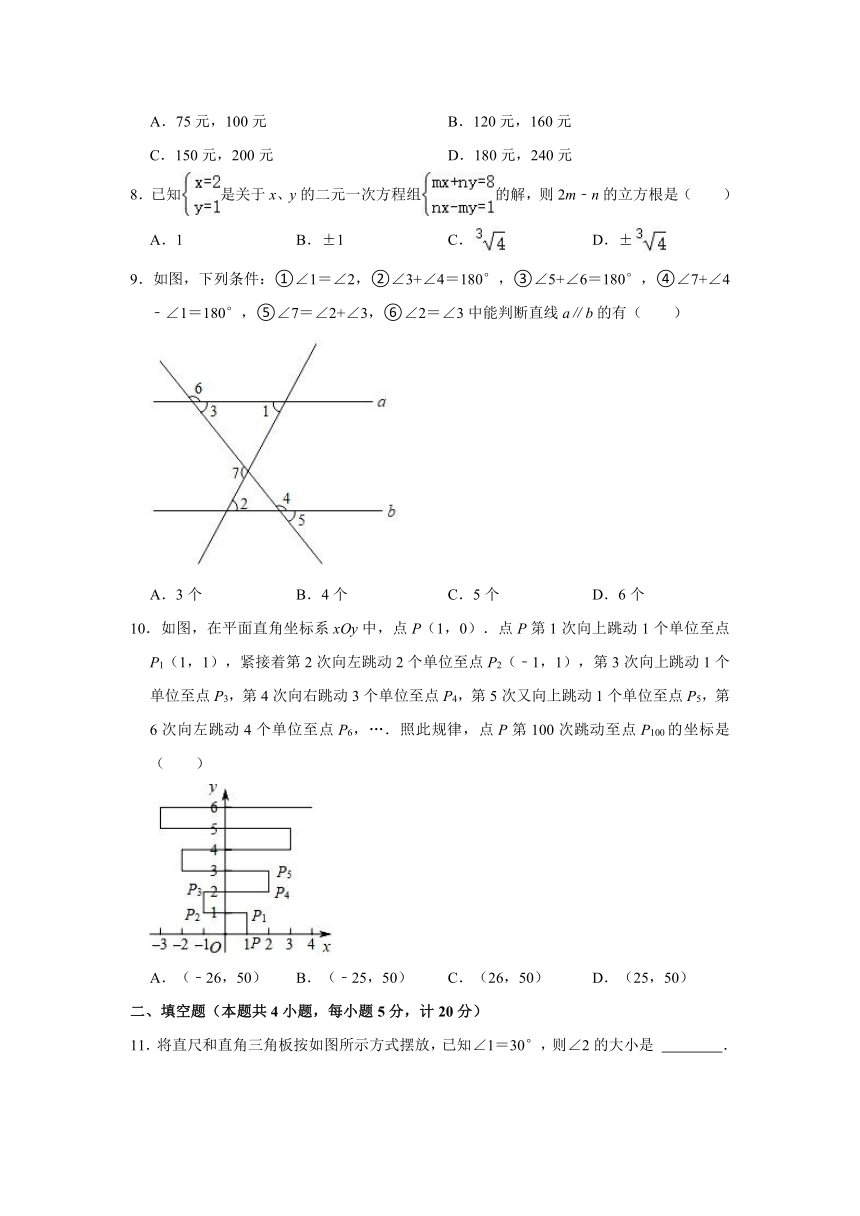
9.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
10.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
A.(﹣26,50) B.(﹣25,50) C.(26,50) D.(25,50)
二、填空题(本题共4小题,每小题5分,计20分)
11.将直尺和直角三角板按如图所示方式摆放,已知∠1=30°,则∠2的大小是 .
12.若不等式(a﹣2)x>a﹣2的解集为x>1,那么字母a的取值范围是 .
13.已知m>0,则在平面直角坐标系中,点M(m,﹣m2﹣1)的位置在第 象限;
14.在《九章算术》中,二元一次方程组是通过“算筹”摆放的.若图中各行从左到右列出的三组算筹分别表示未知数x,y的系数与相应的常数项,如图1表示方程组是,则如图2表示的方程组是 .
三、(本大题共8个题,计90分)
15.解方程组:.
16.x取哪些整数值时,不等式4(x﹣0.3)<0.5x+5.8与x+1≥﹣7﹣x都成立?
17.如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,求证:∠AGF=∠ABC.
试将下面的证明过程补充完整(填空):
证明:∵DE⊥AC,BF⊥AC(已知)
∴∠AFB=∠AED=90°( )
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1= ,(同角的补角相等)
∴GF∥ (内错角相等,两直线平行),
∴∠AGF=∠ABC.( )
18.如图,长方形内有两个相邻的正方形,面积分别为9和6,
(1)小正方形边长的值在哪两个连续的整数之间?与哪个整数较接近?(直接写结果)
(2)求图中阴影部分的面积.
(3)若小正方形边长的值的整数部分为x,小数部分为y,求(y﹣)x的值.
19.如图,在正方形网格中建立平面直角坐标系xOy,使得A,B两点的坐标分别为A(4,1),B(1,﹣2),过点B作BC⊥x轴于点C.
(1)按照要求画出平面直角坐标系xOy,线段BC,写出点C的坐标;
(2)直接写出以A,B,O为顶点的三角形的面积;
(3)若线段CD是由线段AB平移得到的,点A的对应点是C,写出点D的坐标.
20.某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
(1)求购买1个篮球和1个足球各需多少元?
(2)若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
21.为了解男生报考综合素质评价体育测试项目的意向,某校从七年级各班男生随机抽取若干人组成调查样本,根据收集整理到的数据绘制成不完全统计图.根据以上信息,解答下列问题:
项目 男生体育测试项目
A类 1000米1分钟跳绳 立定跳远
B类 1000米立定跳远 实心球
C类 1000实心球 1分钟跳绳
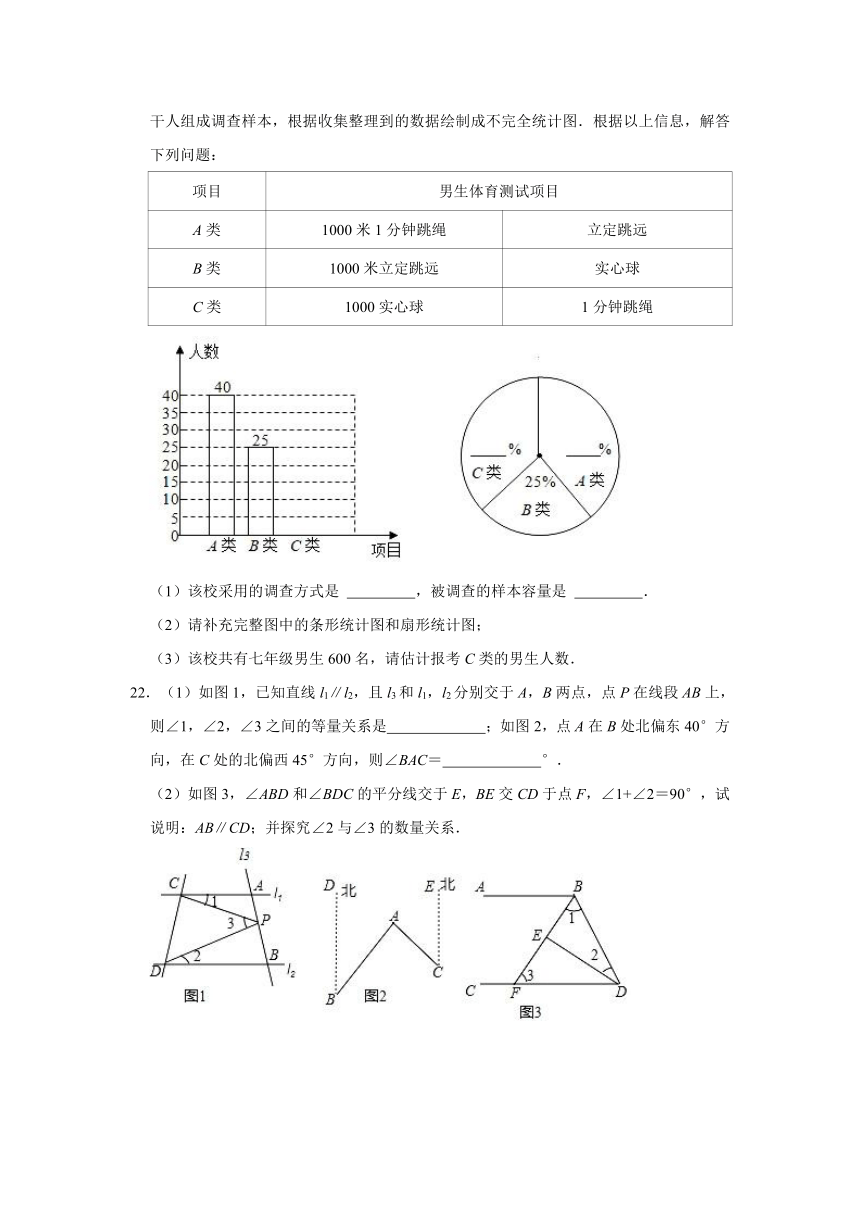
(1)该校采用的调查方式是 ,被调查的样本容量是 .
(2)请补充完整图中的条形统计图和扇形统计图;
(3)该校共有七年级男生600名,请估计报考C类的男生人数.
22.(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是 ;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC= °.
(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.
参考答案
一、选择题(本大题共10个小题,每小题4分,计40分。)
1.计算的平方根为( )
A.±4 B.±2 C.4 D.±
解:∵=4,
又∵(±2)2=4,
∴4的平方根是±2,即的平方根±2.
故选:B.
2.下列调查中:①了解某班学生学习中国共产党党史的情况;②选出某校1000米跑的最快的学生;③了解全国中学生视力情况;④了解长江中鱼的种类.适合采取抽样调查的是( )
A.①③ B.②④ C.①② D.③④
解:①了解某班学生学习中国共产党党史的情况,适合采用全面调查;
②选出某校1000米跑的最快的学生,适合采用全面调查;
③了解全国中学生视力情况,是采用抽样调查;
④了解长江中鱼的种类.适合采用抽样调查;
因此适合采用抽样调查的有:③④,
故选:D.
3.为了迎接端午节,某校食堂推出四种粽子新款(分别以A,B,C,D表示),请学生代表免费试吃选出最喜欢的品种,结果反馈如下:
CDDBABABBBACCBABABCDCD
通过以上数据,你能获得的信息是( )
A.A款粽子最受欢迎
B.B款粽子最受欢迎
C.喜欢C、D两款粽子的人加起来占样本的一半
D.D款粽子受欢迎程度仅次于C款
解:A、B款粽子最受欢迎,故本选项不符合题意;
B、B款粽子最受欢迎,故本选项符合题意;
C、喜欢C、D两款粽子的人加起来少于样本的一半,故本选项不符合题意;
D、D款粽子最不受欢迎,故本选项不符合题意;
故选:B.
4.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
A.10° B.20° C.30° D.40°
解:∵AE∥BD,
∴∠CBD=∠1=120°,
∵∠BDC=∠2=40°,∠C+∠CBD+∠CDB=180°,
∴∠C=20°.
故选:B.
5.已知a<b,则下列各式不成立的是( )
A.a﹣2<b﹣2 B.3a+b<4b C.1﹣2a<1﹣2b D.ac<bc(c>0)
解:A、两边都减2,不等号的方向不变,正确,不符合选项;
B、因为a<b,所以3a+b<4b,正确,不符合选项;
C、因为a<b,所以1﹣2a>1﹣2b,错误,符合选项;
D、因为a<b,所以ac<bc(c>0),正确,不符合选项;
故选:C.
6.关于x的一元一次方程x+m﹣2=0的解是负数,则m的取值范围是( )
A.m>2 B.m<2 C.m>﹣2 D.m<﹣2
解:∵方程x+m﹣2=0的解是负数,
∴x=2﹣m<0,
解得:m>2,
故选:A.
7.打折前购买A商品40件与购买B商品30件所花的钱一样多,商家打折促销,A商品打八折,B商品打九折,此时购买A商品40件比购买B商品30件少花600元,则打折前A商品和B商品每件的价格分别为( )
A.75元,100元 B.120元,160元
C.150元,200元 D.180元,240元
解:设打折前A商品价格为x元,B商品为y元,
根据题意得:,
解得:,
则打折前A商品价格是150元,B商品是200元.
故选:C.
8.已知是关于x、y的二元一次方程组的解,则2m﹣n的立方根是( )
A.1 B.±1 C. D.±
解:∵是方程组的解,
∴,
由①得n=8﹣2m③,
将③代入②,得m=3,
将m=3代入③得,n=2,
∴2m﹣n=6﹣2=4,
∴2m﹣n的立方根是,
故选:C.
9.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠7+∠4﹣∠1=180°,∠7=∠1+∠3,可得∠3+∠4=180°,即可得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠2=∠3,不能得到a∥b;
故能判断直线a∥b的有5个.
故选:C.
10.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
A.(﹣26,50) B.(﹣25,50) C.(26,50) D.(25,50)
解:经过观察可得:P1和P2的纵坐标均为1,P3和P4的纵坐标均为2,P5和P6的纵坐标均为3,因此可以推知P99和P100的纵坐标均为100÷2=50;
其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:Pn的横坐标为n÷4+1(n是4的倍数).
故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).
故选:C.
二、填空题(本题共4小题,每小题5分,计20分)
11.将直尺和直角三角板按如图所示方式摆放,已知∠1=30°,则∠2的大小是 60° .
解:∵∠1+∠3=90°,∠1=30°,
∴∠3=60°.
∵直尺的两边互相平行,
∴∠2=∠3=60°.
故答案为:60°.
12.若不等式(a﹣2)x>a﹣2的解集为x>1,那么字母a的取值范围是 a>2 .
解:∵不等式(a﹣2)x>a﹣2的解集为x>1,
∴a﹣2>0,
∴a>2.
故答案为:a>2.
13.已知m>0,则在平面直角坐标系中,点M(m,﹣m2﹣1)的位置在第 四 象限;
解:∵m>0,
∴﹣m2﹣1<0,
∴点M(m,﹣m2﹣1)的位置在第四象限.
故答案为:四.
14.在《九章算术》中,二元一次方程组是通过“算筹”摆放的.若图中各行从左到右列出的三组算筹分别表示未知数x,y的系数与相应的常数项,如图1表示方程组是,则如图2表示的方程组是 .
解:依题意得:.
故答案为:.
三、(本大题共8个题,计90分)
15.解方程组:.
解:①×3+②,得10x=30,
解得:x=3,
把x=3代入①,得6﹣y=5,
解得:y=1,
所以方程组的解是.
16.x取哪些整数值时,不等式4(x﹣0.3)<0.5x+5.8与x+1≥﹣7﹣x都成立?
解:不等式4(x﹣0.3)<0.5x+5.8,
去括号得:4x﹣1.2<0.5x+5.8,
移项合并得:3.5x<7,
解得:x<2;
不等式x+1≥﹣7﹣x,
去分母得:x+2≥﹣14﹣3x,
解得:x≥﹣4,
∴两不等式的公共解为﹣4≤x<2,
则x取的整数值为﹣4,﹣3,﹣2,﹣1,0,1.
17.如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,求证:∠AGF=∠ABC.
试将下面的证明过程补充完整(填空):
证明:∵DE⊥AC,BF⊥AC(已知)
∴∠AFB=∠AED=90°( 垂直的定义 )
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1= ∠3 ,(同角的补角相等)
∴GF∥ BC (内错角相等,两直线平行),
∴∠AGF=∠ABC.( 两直线平行,同位角相等 )
【解答】证明:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠AED=90° (垂直的定义),
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°,
∴∠1=∠3(同角的补角相等),
∴GF∥BC (内错角相等,两直线平行),
∴∠AGF=∠ABC(两直线平行,同位角相等),
故答案为:垂直的定义、∠3、BC、两直线平行,同位角相等.
18.如图,长方形内有两个相邻的正方形,面积分别为9和6,
(1)小正方形边长的值在哪两个连续的整数之间?与哪个整数较接近?(直接写结果)
(2)求图中阴影部分的面积.
(3)若小正方形边长的值的整数部分为x,小数部分为y,求(y﹣)x的值.
解:(1)∵小正方形的面积为6,
∴小正方形的边长为,
∵4<6<9,
∴2<<3,
∴小正方形的边长在2和3之间;与整数2比较接近.
(2)∵阴影部分的面积的和为一个长为,宽为(3﹣)的矩形面积,
∴阴影部分的面积=.
(3)∵小正方形的边长为,
∴x=2,y=,
∴原式=
=4.
19.如图,在正方形网格中建立平面直角坐标系xOy,使得A,B两点的坐标分别为A(4,1),B(1,﹣2),过点B作BC⊥x轴于点C.
(1)按照要求画出平面直角坐标系xOy,线段BC,写出点C的坐标;
(2)直接写出以A,B,O为顶点的三角形的面积;
(3)若线段CD是由线段AB平移得到的,点A的对应点是C,写出点D的坐标.
解:(1)平面直角坐标系如图所示:C(1,0).
(2)S△AOB=3×4﹣×1×4﹣×1×2﹣×3×3=.
(3)D(﹣2,﹣3).
20.某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
(1)求购买1个篮球和1个足球各需多少元?
(2)若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
解:(1)设购买一个篮球的需x元,购买一个足球的需 y元,
依题意得,
解得,
答:购买一个篮球需60元,购买一个足球需28元;
(2)设购买m个篮球,则足球数为(40﹣m),
依题意得:60m+28(40﹣m)≤1800,
解得:m≤,
而m为正整数,
m最多=21,
答:篮球最多可购买21个.
21.为了解男生报考综合素质评价体育测试项目的意向,某校从七年级各班男生随机抽取若干人组成调查样本,根据收集整理到的数据绘制成不完全统计图.根据以上信息,解答下列问题:
项目 男生体育测试项目
A类 1000米1分钟跳绳 立定跳远
B类 1000米立定跳远 实心球
C类 1000实心球 1分钟跳绳
(1)该校采用的调查方式是 抽样调查 ,被调查的样本容量是 100 .
(2)请补充完整图中的条形统计图和扇形统计图;
(3)该校共有七年级男生600名,请估计报考C类的男生人数.
解:(1)该小组采用的调查方式是:抽样调查,
被调查的样本容量是:25÷25%=100人,
故答案为:抽样调查,100;
(2)如图所示:
C类人数:100﹣40﹣25=35人,
C类所占百分比:×100%=35%,
C类所占百分比:1﹣35%﹣25%=40%,
(3)可以估计报考A类的男生人数约为:600×35%=210(人).
22.(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是 ∠3=∠1+∠2 ;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC= 85 °.
(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.
解:(1)如图1中,作PM∥AC,
∵AC∥BD,
∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
由题可知:∠BAC=∠B+∠C,
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
故答案为:∠1+∠2=∠3,85°.
(2)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1=∠ABD,∠2=∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
一、选择题(共10个小题,每小题4分).
1.计算的平方根为( )
A.±4 B.±2 C.4 D.±
2.下列调查中:①了解某班学生学习中国共产党党史的情况;②选出某校1000米跑的最快的学生;③了解全国中学生视力情况;④了解长江中鱼的种类.适合采取抽样调查的是( )
A.①③ B.②④ C.①② D.③④
3.为了迎接端午节,某校食堂推出四种粽子新款(分别以A,B,C,D表示),请学生代表免费试吃选出最喜欢的品种,结果反馈如下:
CDDBABABBBACCBABABCDCD
通过以上数据,你能获得的信息是( )
A.A款粽子最受欢迎
B.B款粽子最受欢迎
C.喜欢C、D两款粽子的人加起来占样本的一半
D.D款粽子受欢迎程度仅次于C款
4.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
A.10° B.20° C.30° D.40°
5.已知a<b,则下列各式不成立的是( )
A.a﹣2<b﹣2 B.3a+b<4b C.1﹣2a<1﹣2b D.ac<bc(c>0)
6.关于x的一元一次方程x+m﹣2=0的解是负数,则m的取值范围是( )
A.m>2 B.m<2 C.m>﹣2 D.m<﹣2
7.打折前购买A商品40件与购买B商品30件所花的钱一样多,商家打折促销,A商品打八折,B商品打九折,此时购买A商品40件比购买B商品30件少花600元,则打折前A商品和B商品每件的价格分别为( )
A.75元,100元 B.120元,160元
C.150元,200元 D.180元,240元
8.已知是关于x、y的二元一次方程组的解,则2m﹣n的立方根是( )
A.1 B.±1 C. D.±
9.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
10.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
A.(﹣26,50) B.(﹣25,50) C.(26,50) D.(25,50)
二、填空题(本题共4小题,每小题5分,计20分)
11.将直尺和直角三角板按如图所示方式摆放,已知∠1=30°,则∠2的大小是 .
12.若不等式(a﹣2)x>a﹣2的解集为x>1,那么字母a的取值范围是 .
13.已知m>0,则在平面直角坐标系中,点M(m,﹣m2﹣1)的位置在第 象限;
14.在《九章算术》中,二元一次方程组是通过“算筹”摆放的.若图中各行从左到右列出的三组算筹分别表示未知数x,y的系数与相应的常数项,如图1表示方程组是,则如图2表示的方程组是 .
三、(本大题共8个题,计90分)
15.解方程组:.
16.x取哪些整数值时,不等式4(x﹣0.3)<0.5x+5.8与x+1≥﹣7﹣x都成立?
17.如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,求证:∠AGF=∠ABC.
试将下面的证明过程补充完整(填空):
证明:∵DE⊥AC,BF⊥AC(已知)
∴∠AFB=∠AED=90°( )
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1= ,(同角的补角相等)
∴GF∥ (内错角相等,两直线平行),
∴∠AGF=∠ABC.( )
18.如图,长方形内有两个相邻的正方形,面积分别为9和6,
(1)小正方形边长的值在哪两个连续的整数之间?与哪个整数较接近?(直接写结果)
(2)求图中阴影部分的面积.
(3)若小正方形边长的值的整数部分为x,小数部分为y,求(y﹣)x的值.
19.如图,在正方形网格中建立平面直角坐标系xOy,使得A,B两点的坐标分别为A(4,1),B(1,﹣2),过点B作BC⊥x轴于点C.
(1)按照要求画出平面直角坐标系xOy,线段BC,写出点C的坐标;
(2)直接写出以A,B,O为顶点的三角形的面积;
(3)若线段CD是由线段AB平移得到的,点A的对应点是C,写出点D的坐标.
20.某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
(1)求购买1个篮球和1个足球各需多少元?
(2)若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
21.为了解男生报考综合素质评价体育测试项目的意向,某校从七年级各班男生随机抽取若干人组成调查样本,根据收集整理到的数据绘制成不完全统计图.根据以上信息,解答下列问题:
项目 男生体育测试项目
A类 1000米1分钟跳绳 立定跳远
B类 1000米立定跳远 实心球
C类 1000实心球 1分钟跳绳
(1)该校采用的调查方式是 ,被调查的样本容量是 .
(2)请补充完整图中的条形统计图和扇形统计图;
(3)该校共有七年级男生600名,请估计报考C类的男生人数.
22.(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是 ;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC= °.
(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.
参考答案
一、选择题(本大题共10个小题,每小题4分,计40分。)
1.计算的平方根为( )
A.±4 B.±2 C.4 D.±
解:∵=4,
又∵(±2)2=4,
∴4的平方根是±2,即的平方根±2.
故选:B.
2.下列调查中:①了解某班学生学习中国共产党党史的情况;②选出某校1000米跑的最快的学生;③了解全国中学生视力情况;④了解长江中鱼的种类.适合采取抽样调查的是( )
A.①③ B.②④ C.①② D.③④
解:①了解某班学生学习中国共产党党史的情况,适合采用全面调查;
②选出某校1000米跑的最快的学生,适合采用全面调查;
③了解全国中学生视力情况,是采用抽样调查;
④了解长江中鱼的种类.适合采用抽样调查;
因此适合采用抽样调查的有:③④,
故选:D.
3.为了迎接端午节,某校食堂推出四种粽子新款(分别以A,B,C,D表示),请学生代表免费试吃选出最喜欢的品种,结果反馈如下:
CDDBABABBBACCBABABCDCD
通过以上数据,你能获得的信息是( )
A.A款粽子最受欢迎
B.B款粽子最受欢迎
C.喜欢C、D两款粽子的人加起来占样本的一半
D.D款粽子受欢迎程度仅次于C款
解:A、B款粽子最受欢迎,故本选项不符合题意;
B、B款粽子最受欢迎,故本选项符合题意;
C、喜欢C、D两款粽子的人加起来少于样本的一半,故本选项不符合题意;
D、D款粽子最不受欢迎,故本选项不符合题意;
故选:B.
4.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
A.10° B.20° C.30° D.40°
解:∵AE∥BD,
∴∠CBD=∠1=120°,
∵∠BDC=∠2=40°,∠C+∠CBD+∠CDB=180°,
∴∠C=20°.
故选:B.
5.已知a<b,则下列各式不成立的是( )
A.a﹣2<b﹣2 B.3a+b<4b C.1﹣2a<1﹣2b D.ac<bc(c>0)
解:A、两边都减2,不等号的方向不变,正确,不符合选项;
B、因为a<b,所以3a+b<4b,正确,不符合选项;
C、因为a<b,所以1﹣2a>1﹣2b,错误,符合选项;
D、因为a<b,所以ac<bc(c>0),正确,不符合选项;
故选:C.
6.关于x的一元一次方程x+m﹣2=0的解是负数,则m的取值范围是( )
A.m>2 B.m<2 C.m>﹣2 D.m<﹣2
解:∵方程x+m﹣2=0的解是负数,
∴x=2﹣m<0,
解得:m>2,
故选:A.
7.打折前购买A商品40件与购买B商品30件所花的钱一样多,商家打折促销,A商品打八折,B商品打九折,此时购买A商品40件比购买B商品30件少花600元,则打折前A商品和B商品每件的价格分别为( )
A.75元,100元 B.120元,160元
C.150元,200元 D.180元,240元
解:设打折前A商品价格为x元,B商品为y元,
根据题意得:,
解得:,
则打折前A商品价格是150元,B商品是200元.
故选:C.
8.已知是关于x、y的二元一次方程组的解,则2m﹣n的立方根是( )
A.1 B.±1 C. D.±
解:∵是方程组的解,
∴,
由①得n=8﹣2m③,
将③代入②,得m=3,
将m=3代入③得,n=2,
∴2m﹣n=6﹣2=4,
∴2m﹣n的立方根是,
故选:C.
9.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠7+∠4﹣∠1=180°,∠7=∠1+∠3,可得∠3+∠4=180°,即可得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠2=∠3,不能得到a∥b;
故能判断直线a∥b的有5个.
故选:C.
10.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
A.(﹣26,50) B.(﹣25,50) C.(26,50) D.(25,50)
解:经过观察可得:P1和P2的纵坐标均为1,P3和P4的纵坐标均为2,P5和P6的纵坐标均为3,因此可以推知P99和P100的纵坐标均为100÷2=50;
其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:Pn的横坐标为n÷4+1(n是4的倍数).
故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).
故选:C.
二、填空题(本题共4小题,每小题5分,计20分)
11.将直尺和直角三角板按如图所示方式摆放,已知∠1=30°,则∠2的大小是 60° .
解:∵∠1+∠3=90°,∠1=30°,
∴∠3=60°.
∵直尺的两边互相平行,
∴∠2=∠3=60°.
故答案为:60°.
12.若不等式(a﹣2)x>a﹣2的解集为x>1,那么字母a的取值范围是 a>2 .
解:∵不等式(a﹣2)x>a﹣2的解集为x>1,
∴a﹣2>0,
∴a>2.
故答案为:a>2.
13.已知m>0,则在平面直角坐标系中,点M(m,﹣m2﹣1)的位置在第 四 象限;
解:∵m>0,
∴﹣m2﹣1<0,
∴点M(m,﹣m2﹣1)的位置在第四象限.
故答案为:四.
14.在《九章算术》中,二元一次方程组是通过“算筹”摆放的.若图中各行从左到右列出的三组算筹分别表示未知数x,y的系数与相应的常数项,如图1表示方程组是,则如图2表示的方程组是 .
解:依题意得:.
故答案为:.
三、(本大题共8个题,计90分)
15.解方程组:.
解:①×3+②,得10x=30,
解得:x=3,
把x=3代入①,得6﹣y=5,
解得:y=1,
所以方程组的解是.
16.x取哪些整数值时,不等式4(x﹣0.3)<0.5x+5.8与x+1≥﹣7﹣x都成立?
解:不等式4(x﹣0.3)<0.5x+5.8,
去括号得:4x﹣1.2<0.5x+5.8,
移项合并得:3.5x<7,
解得:x<2;
不等式x+1≥﹣7﹣x,
去分母得:x+2≥﹣14﹣3x,
解得:x≥﹣4,
∴两不等式的公共解为﹣4≤x<2,
则x取的整数值为﹣4,﹣3,﹣2,﹣1,0,1.
17.如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,求证:∠AGF=∠ABC.
试将下面的证明过程补充完整(填空):
证明:∵DE⊥AC,BF⊥AC(已知)
∴∠AFB=∠AED=90°( 垂直的定义 )
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1= ∠3 ,(同角的补角相等)
∴GF∥ BC (内错角相等,两直线平行),
∴∠AGF=∠ABC.( 两直线平行,同位角相等 )
【解答】证明:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠AED=90° (垂直的定义),
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°,
∴∠1=∠3(同角的补角相等),
∴GF∥BC (内错角相等,两直线平行),
∴∠AGF=∠ABC(两直线平行,同位角相等),
故答案为:垂直的定义、∠3、BC、两直线平行,同位角相等.
18.如图,长方形内有两个相邻的正方形,面积分别为9和6,
(1)小正方形边长的值在哪两个连续的整数之间?与哪个整数较接近?(直接写结果)
(2)求图中阴影部分的面积.
(3)若小正方形边长的值的整数部分为x,小数部分为y,求(y﹣)x的值.
解:(1)∵小正方形的面积为6,
∴小正方形的边长为,
∵4<6<9,
∴2<<3,
∴小正方形的边长在2和3之间;与整数2比较接近.
(2)∵阴影部分的面积的和为一个长为,宽为(3﹣)的矩形面积,
∴阴影部分的面积=.
(3)∵小正方形的边长为,
∴x=2,y=,
∴原式=
=4.
19.如图,在正方形网格中建立平面直角坐标系xOy,使得A,B两点的坐标分别为A(4,1),B(1,﹣2),过点B作BC⊥x轴于点C.
(1)按照要求画出平面直角坐标系xOy,线段BC,写出点C的坐标;
(2)直接写出以A,B,O为顶点的三角形的面积;
(3)若线段CD是由线段AB平移得到的,点A的对应点是C,写出点D的坐标.
解:(1)平面直角坐标系如图所示:C(1,0).
(2)S△AOB=3×4﹣×1×4﹣×1×2﹣×3×3=.
(3)D(﹣2,﹣3).
20.某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
(1)求购买1个篮球和1个足球各需多少元?
(2)若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
解:(1)设购买一个篮球的需x元,购买一个足球的需 y元,
依题意得,
解得,
答:购买一个篮球需60元,购买一个足球需28元;
(2)设购买m个篮球,则足球数为(40﹣m),
依题意得:60m+28(40﹣m)≤1800,
解得:m≤,
而m为正整数,
m最多=21,
答:篮球最多可购买21个.
21.为了解男生报考综合素质评价体育测试项目的意向,某校从七年级各班男生随机抽取若干人组成调查样本,根据收集整理到的数据绘制成不完全统计图.根据以上信息,解答下列问题:
项目 男生体育测试项目
A类 1000米1分钟跳绳 立定跳远
B类 1000米立定跳远 实心球
C类 1000实心球 1分钟跳绳
(1)该校采用的调查方式是 抽样调查 ,被调查的样本容量是 100 .
(2)请补充完整图中的条形统计图和扇形统计图;
(3)该校共有七年级男生600名,请估计报考C类的男生人数.
解:(1)该小组采用的调查方式是:抽样调查,
被调查的样本容量是:25÷25%=100人,
故答案为:抽样调查,100;
(2)如图所示:
C类人数:100﹣40﹣25=35人,
C类所占百分比:×100%=35%,
C类所占百分比:1﹣35%﹣25%=40%,
(3)可以估计报考A类的男生人数约为:600×35%=210(人).
22.(1)如图1,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在线段AB上,则∠1,∠2,∠3之间的等量关系是 ∠3=∠1+∠2 ;如图2,点A在B处北偏东40°方向,在C处的北偏西45°方向,则∠BAC= 85 °.
(2)如图3,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°,试说明:AB∥CD;并探究∠2与∠3的数量关系.
解:(1)如图1中,作PM∥AC,
∵AC∥BD,
∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
由题可知:∠BAC=∠B+∠C,
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
故答案为:∠1+∠2=∠3,85°.
(2)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1=∠ABD,∠2=∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
同课章节目录
