22.1.2 二次函数y=ax2的图象和性质-2021至2022学年度人教版九年级数学上册新考向多视角同步训练(含解析)
文档属性
| 名称 | 22.1.2 二次函数y=ax2的图象和性质-2021至2022学年度人教版九年级数学上册新考向多视角同步训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 10:00:36 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十二章 二次函数
22.1 二次函数的图像和性质
22.1.2 二次函数y=ax2的图像和性质
知识能力全练
知识点 二次函数y=ax2的图象和性质
1.下表是二次函数y=ax2的部分x,y的对应值:
则下列说法不正确的是 ( )
A.图象开口向上 B.图象对称轴是y轴 C.图象顶点是原点 D.图象经过点(-3,6)
2.(2021安徽六安金安期中)抛物线y=x2,y=-3x2,y=x2的共同性质是 ( )
A.开口都向上 B.都有最大值 C.对称轴都是x轴 D.顶点都是原点
3.(2020河北保定蠡县期中)已知y=(k-1)xk-2是关于x的二次函数,且有最大值,则k= ( )
A.-2 B.2 C.1 D.-1
4.(2020湖南长沙雨花期末)在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致为 ( )
5.二次函数y=mxm-1,若在其图象的对称轴的左侧,y随x的增大而增大,则下列各点不在其图象上的是 ( )
A.(1,-3) B.(-1,-3) C.(0,0) D.(-1,3)
6.函数y=(m-2)xm m-2是二次函数,则下列关于它的图象的说法:①开口向上;②开口向下;③对称轴是y轴;④顶点坐标为(0,0);⑤顶点坐标为(0,-4);⑥顶点坐标为(-4,0);⑦有最高点;⑧有最低点,其中正确的有 ( )
A.3个 B.4个 C.5个 D.6个
7.若二次函数y=ax2的图象过点A(1,-2),点A与点B关于该图象的对称轴对称,则点B的坐标是________。
8.对于二次函数y=ax2(a≠0),当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为________。
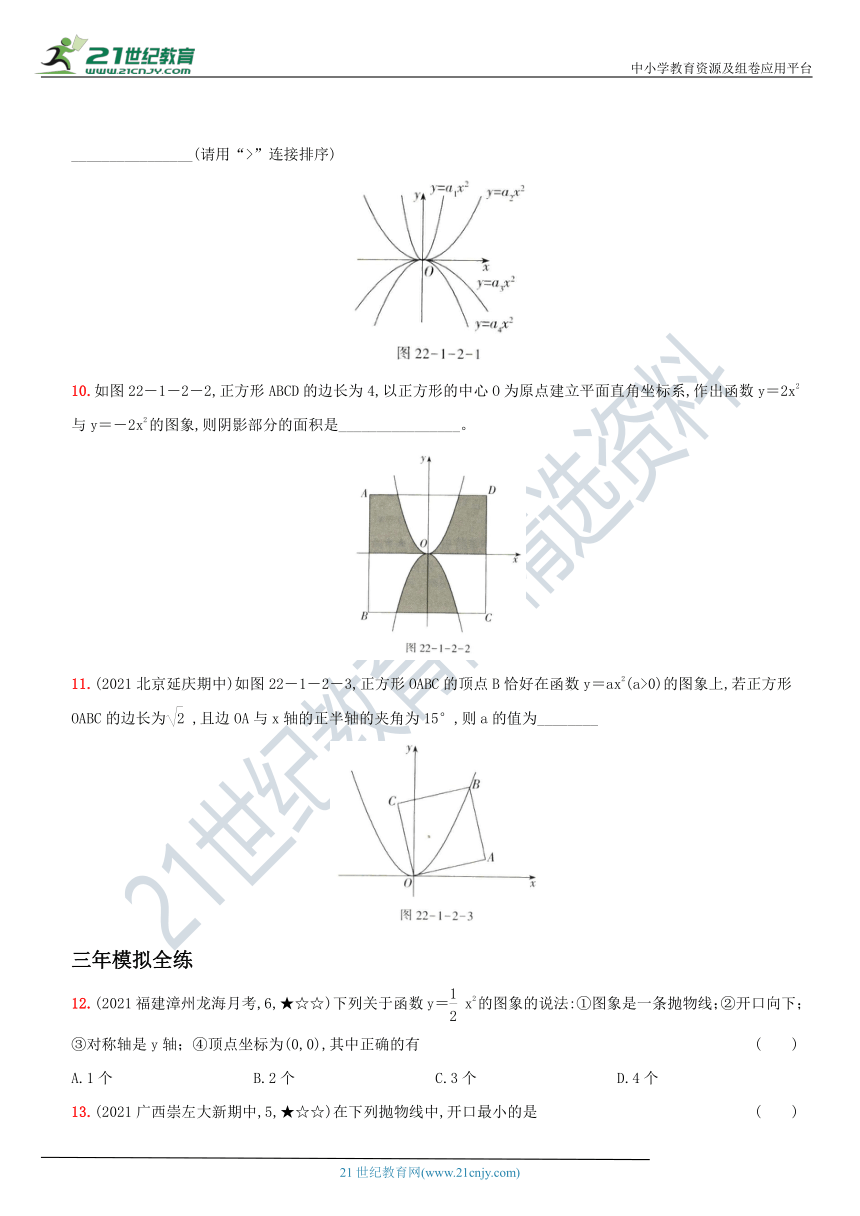
9.(2020内蒙古呼和浩特期中)已知四个二次函数的图象如图22-1-2-1所示,那么a1,a2,a3,a4的大小关系是________________(请用“>”连接排序)
10.如图22-1-2-2,正方形ABCD的边长为4,以正方形的中心O为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是________________。
11.(2021北京延庆期中)如图22-1-2-3,正方形OABC的顶点B恰好在函数y=ax2(a>0)的图象上,若正方形OABC的边长为,且边OA与x轴的正半轴的夹角为15°,则a的值为________
三年模拟全练
12.(2021福建漳州龙海月考,6,★☆☆)下列关于函数y=x2的图象的说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点坐标为(0,0),其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
13.(2021广西崇左大新期中,5,★☆☆)在下列抛物线中,开口最小的是 ( )
A.y=-x2 B.y=-x C.y=x2 D.y=x2
14.(2020河南漯河郾城期中,5,★★☆)已知A(1,y1),B(-2,y2)、C(-,y3)在函数y=x2的图象上,则y1、y2、y3的大小关系是 ( )
A.y1五年中考全练
15.(2019湖南益阳中考,5,★☆☆)下列函数中,y总随x的增大而减小的是 ( )
A.y=4x B.y=-4x C.y=x-4 D.y=x2
16.(2019内蒙古呼和浩特中考,3,★★☆)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是 ( )
核心素养全练
17.定义运算“※”,a※b=,如:1※(-2)=-1×(-2)2=-4,则函数y=2※x的图象大致是 ( )
18.如图22-1-2-4,在抛物线y=ax2上有点A(-2,4),过点A作x轴的平行线交抛物线于点B,点C为抛物线上的动点(不与点A、B重合),连接CA,BC,取线段AC,BC的中点D,E,连接DE.当点C在抛物线上运动时,下列结论正确的为________(填写序号即可)
①AB=4;②DE=2;③S△CAB=8;S△CDE=2;⑤△ACB的周长为4+4.
《参考答案及解析》
22.1.2 二次函数y=ax2的图象和性质
知识能力全练
1.D 形如y=ax2(a≠0)的函数图象的对称轴都是y轴,顶点都是原点,从表格中数值的变化趋势可知,图象开口向上,∴选项A,B,C中说法都正确.把(1,1)代入y=ax2,得a=1,则函数为y=x2,把x=-3代入y=x2,得y=(-3)2=9,∴图象不经过点(-3,6).故选D.
2.D 抛物线y=x2的开口向上,有最小值对称轴是y轴,顶点坐标为(0,0);抛物线y=-3x2的开口向下,有最大值,对称轴是y轴顶点坐标为(0,0);抛物线y=x2的开口向上,最小值,对称轴是y轴,顶点坐标为(0,0),∴三条抛物线的共同性质是顶点都是原点.故选D.
3.A 由二次函数的定义可知k-1≠0,且k2-2=2,∴k=±2函数有最大值,∴k-1<0,即k<1,∴k=-2.故选A.
4.D 一次函数y=kx+2的图象与y轴正半轴相交,故A、B错误;当k>0时,函数y=kx2的图象开口向上,一次函数y=kx+2(k≠0)的图象经过第一、二、三象限,故C错误,D符合题意.故选D
5.D 由题意得m<0,且m2-1=2,解得m=-.把x=1代入y=-x2,得y=-,则点(1,-)在其图象上;把x=-1代入y=-x2,得y=-,则点(-1,-)在其图象上,点(-1,)不在其图象上;点(0,0)是该二次函数图象的顶点,在其图象上.故选D
6.B 由二次函数的概念可得m2-2=2且m-2≠0,解得m=-2,则函数为y=-4x2,所以它的图象开口向下,对称轴是y轴,顶点坐标为(0,0),有最高点,即②③④⑦正确.
7.【答案】(-1,-2)
【解析】抛物线y=ax2的对称轴是y轴,A(1,-2)关于y轴的对称点的坐标为(-1,-2)
8.【答案】0
【解析】∵二次函数y=ax2图象的对称轴为y轴,当x取x1,x2(x1≠x2)时,函数值相等,∴直线x=x1,x=x2关于y轴对称,∴x1+x2=0,又当x=0时,y=0,∴当x取x1+x2时,函数值为0.
9.【答案】a1>a2>a3>a4
【解析】由题图可知y=a1x2的图象开口小于=a2x2的图象开口,且两函数图象都开口向上,则a1>a2>0;y=a3x2的图象开口大于y=a4x2的图象开口,且两函数图象都开口向下,则a4a2>a3>a4
10.【答案】8
【解析】∵函数y=2x2与y=-2x2的图象关于x轴对称,
∴题图中阴影部分的面积是题图中正方形ABCD面积的一半,
∴S阴影=×42=8,即题图中阴影部分的面积是8.
11.【答案】
【解析】如图,连接OB,过B作BD⊥x轴于D,则∠BOA=45°,∠BOD=60°,已知正方形的边长为,则OB=2.Rt△OBD中,OB=2,∠BOD=60°,则∠OBD=30°,∴OD=OB=1,∴BD=,故B(1,),将B(1,)代入y=ax2中,得a=.
三年模拟全练
12.C ∵函数为y=x2,∴该函数图象是一条抛物线,故①正确;∵a=>0,∴该函数图象开口向上,故②错误;对称轴是y轴,故③正确;顶点坐标为(0,0),故④正确故选C.
13.D eq \x \ri \le (-) < eq \x \ri \le (-) << eq \x \ri \le () ,∴函数y=x2的图象的开口最小.故选D.
14.A 解法一:函数y=x2的图象是以y轴为对称轴,开口向上的抛
物线,∴点离y轴越远,函数值越大∵< eq \x \ri \le (-) <,∴y1解法二∵A(1,y1),B(-2,y2)、C(-,y3)在函数y=x2的图象上,
∴y1=1,y2=(-2)2=4,y3=(-)2=2,∴y1五年中考全练
15.B y=4x是一次函数,4>0,y随x的增大而增大;y=-4x是一次函数,-4<0,y随x的增大而减小;y=x-4是一次函数,1>0,y随x的增大而增大;y=x2是二次函数,1>0,当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.故选B.
16.D 由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A、B;当a>0时,二次函数y=ax2的图象开口向上,一次函数y=ax+a的图象经过第一、二、三象限;当a<0时,二次函数y=ax2的图象开口向下,一次函数y=ax+a的图象经过第二、三、四象限,排除C.故选D.
核心素养全练
17.C y=2※x=,当x>0时,图象是y=2x2图象的对称轴右侧的部分;当x≤0时,图象是y=-2x2图象的对称轴上及其左侧的部分,故选C.
18.【答案】①②
【解析】∵抛物线y=ax2关于y轴对称,AB∥x轴∴点B与点A关于y轴对称,又点A的坐标为(-2,4),∴点B的坐标为(2,4),∴AB=4,故①正确∵D,E分别为AC,BC的中点∴DE为△ABC的中位线,∴DE=AB=2,故②正确;∵点C为动点,∴点C到AB、DE的距离不确定,∴△CAB和△CDE的面积不确定,故③④错误;∵点C是动点,∴AC+BC不确定,∴△ACB的周长不确定(当点C与点O重合时,△ACB的周长为4+4),故⑤错误
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二十二章 二次函数
22.1 二次函数的图像和性质
22.1.2 二次函数y=ax2的图像和性质
知识能力全练
知识点 二次函数y=ax2的图象和性质
1.下表是二次函数y=ax2的部分x,y的对应值:
则下列说法不正确的是 ( )
A.图象开口向上 B.图象对称轴是y轴 C.图象顶点是原点 D.图象经过点(-3,6)
2.(2021安徽六安金安期中)抛物线y=x2,y=-3x2,y=x2的共同性质是 ( )
A.开口都向上 B.都有最大值 C.对称轴都是x轴 D.顶点都是原点
3.(2020河北保定蠡县期中)已知y=(k-1)xk-2是关于x的二次函数,且有最大值,则k= ( )
A.-2 B.2 C.1 D.-1
4.(2020湖南长沙雨花期末)在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致为 ( )
5.二次函数y=mxm-1,若在其图象的对称轴的左侧,y随x的增大而增大,则下列各点不在其图象上的是 ( )
A.(1,-3) B.(-1,-3) C.(0,0) D.(-1,3)
6.函数y=(m-2)xm m-2是二次函数,则下列关于它的图象的说法:①开口向上;②开口向下;③对称轴是y轴;④顶点坐标为(0,0);⑤顶点坐标为(0,-4);⑥顶点坐标为(-4,0);⑦有最高点;⑧有最低点,其中正确的有 ( )
A.3个 B.4个 C.5个 D.6个
7.若二次函数y=ax2的图象过点A(1,-2),点A与点B关于该图象的对称轴对称,则点B的坐标是________。
8.对于二次函数y=ax2(a≠0),当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为________。
9.(2020内蒙古呼和浩特期中)已知四个二次函数的图象如图22-1-2-1所示,那么a1,a2,a3,a4的大小关系是________________(请用“>”连接排序)
10.如图22-1-2-2,正方形ABCD的边长为4,以正方形的中心O为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是________________。
11.(2021北京延庆期中)如图22-1-2-3,正方形OABC的顶点B恰好在函数y=ax2(a>0)的图象上,若正方形OABC的边长为,且边OA与x轴的正半轴的夹角为15°,则a的值为________
三年模拟全练
12.(2021福建漳州龙海月考,6,★☆☆)下列关于函数y=x2的图象的说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点坐标为(0,0),其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
13.(2021广西崇左大新期中,5,★☆☆)在下列抛物线中,开口最小的是 ( )
A.y=-x2 B.y=-x C.y=x2 D.y=x2
14.(2020河南漯河郾城期中,5,★★☆)已知A(1,y1),B(-2,y2)、C(-,y3)在函数y=x2的图象上,则y1、y2、y3的大小关系是 ( )
A.y1
15.(2019湖南益阳中考,5,★☆☆)下列函数中,y总随x的增大而减小的是 ( )
A.y=4x B.y=-4x C.y=x-4 D.y=x2
16.(2019内蒙古呼和浩特中考,3,★★☆)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是 ( )
核心素养全练
17.定义运算“※”,a※b=,如:1※(-2)=-1×(-2)2=-4,则函数y=2※x的图象大致是 ( )
18.如图22-1-2-4,在抛物线y=ax2上有点A(-2,4),过点A作x轴的平行线交抛物线于点B,点C为抛物线上的动点(不与点A、B重合),连接CA,BC,取线段AC,BC的中点D,E,连接DE.当点C在抛物线上运动时,下列结论正确的为________(填写序号即可)
①AB=4;②DE=2;③S△CAB=8;S△CDE=2;⑤△ACB的周长为4+4.
《参考答案及解析》
22.1.2 二次函数y=ax2的图象和性质
知识能力全练
1.D 形如y=ax2(a≠0)的函数图象的对称轴都是y轴,顶点都是原点,从表格中数值的变化趋势可知,图象开口向上,∴选项A,B,C中说法都正确.把(1,1)代入y=ax2,得a=1,则函数为y=x2,把x=-3代入y=x2,得y=(-3)2=9,∴图象不经过点(-3,6).故选D.
2.D 抛物线y=x2的开口向上,有最小值对称轴是y轴,顶点坐标为(0,0);抛物线y=-3x2的开口向下,有最大值,对称轴是y轴顶点坐标为(0,0);抛物线y=x2的开口向上,最小值,对称轴是y轴,顶点坐标为(0,0),∴三条抛物线的共同性质是顶点都是原点.故选D.
3.A 由二次函数的定义可知k-1≠0,且k2-2=2,∴k=±2函数有最大值,∴k-1<0,即k<1,∴k=-2.故选A.
4.D 一次函数y=kx+2的图象与y轴正半轴相交,故A、B错误;当k>0时,函数y=kx2的图象开口向上,一次函数y=kx+2(k≠0)的图象经过第一、二、三象限,故C错误,D符合题意.故选D
5.D 由题意得m<0,且m2-1=2,解得m=-.把x=1代入y=-x2,得y=-,则点(1,-)在其图象上;把x=-1代入y=-x2,得y=-,则点(-1,-)在其图象上,点(-1,)不在其图象上;点(0,0)是该二次函数图象的顶点,在其图象上.故选D
6.B 由二次函数的概念可得m2-2=2且m-2≠0,解得m=-2,则函数为y=-4x2,所以它的图象开口向下,对称轴是y轴,顶点坐标为(0,0),有最高点,即②③④⑦正确.
7.【答案】(-1,-2)
【解析】抛物线y=ax2的对称轴是y轴,A(1,-2)关于y轴的对称点的坐标为(-1,-2)
8.【答案】0
【解析】∵二次函数y=ax2图象的对称轴为y轴,当x取x1,x2(x1≠x2)时,函数值相等,∴直线x=x1,x=x2关于y轴对称,∴x1+x2=0,又当x=0时,y=0,∴当x取x1+x2时,函数值为0.
9.【答案】a1>a2>a3>a4
【解析】由题图可知y=a1x2的图象开口小于=a2x2的图象开口,且两函数图象都开口向上,则a1>a2>0;y=a3x2的图象开口大于y=a4x2的图象开口,且两函数图象都开口向下,则a4
10.【答案】8
【解析】∵函数y=2x2与y=-2x2的图象关于x轴对称,
∴题图中阴影部分的面积是题图中正方形ABCD面积的一半,
∴S阴影=×42=8,即题图中阴影部分的面积是8.
11.【答案】
【解析】如图,连接OB,过B作BD⊥x轴于D,则∠BOA=45°,∠BOD=60°,已知正方形的边长为,则OB=2.Rt△OBD中,OB=2,∠BOD=60°,则∠OBD=30°,∴OD=OB=1,∴BD=,故B(1,),将B(1,)代入y=ax2中,得a=.
三年模拟全练
12.C ∵函数为y=x2,∴该函数图象是一条抛物线,故①正确;∵a=>0,∴该函数图象开口向上,故②错误;对称轴是y轴,故③正确;顶点坐标为(0,0),故④正确故选C.
13.D eq \x \ri \le (-) < eq \x \ri \le (-) << eq \x \ri \le () ,∴函数y=x2的图象的开口最小.故选D.
14.A 解法一:函数y=x2的图象是以y轴为对称轴,开口向上的抛
物线,∴点离y轴越远,函数值越大∵< eq \x \ri \le (-) <,∴y1
∴y1=1,y2=(-2)2=4,y3=(-)2=2,∴y1
15.B y=4x是一次函数,4>0,y随x的增大而增大;y=-4x是一次函数,-4<0,y随x的增大而减小;y=x-4是一次函数,1>0,y随x的增大而增大;y=x2是二次函数,1>0,当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.故选B.
16.D 由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A、B;当a>0时,二次函数y=ax2的图象开口向上,一次函数y=ax+a的图象经过第一、二、三象限;当a<0时,二次函数y=ax2的图象开口向下,一次函数y=ax+a的图象经过第二、三、四象限,排除C.故选D.
核心素养全练
17.C y=2※x=,当x>0时,图象是y=2x2图象的对称轴右侧的部分;当x≤0时,图象是y=-2x2图象的对称轴上及其左侧的部分,故选C.
18.【答案】①②
【解析】∵抛物线y=ax2关于y轴对称,AB∥x轴∴点B与点A关于y轴对称,又点A的坐标为(-2,4),∴点B的坐标为(2,4),∴AB=4,故①正确∵D,E分别为AC,BC的中点∴DE为△ABC的中位线,∴DE=AB=2,故②正确;∵点C为动点,∴点C到AB、DE的距离不确定,∴△CAB和△CDE的面积不确定,故③④错误;∵点C是动点,∴AC+BC不确定,∴△ACB的周长不确定(当点C与点O重合时,△ACB的周长为4+4),故⑤错误
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
