22.1.4 二次函数y=ax2+bx+c的图像象和性质-2021至2022学年度人教版九年级数学上册新考向多视角同步训练(含解析)
文档属性
| 名称 | 22.1.4 二次函数y=ax2+bx+c的图像象和性质-2021至2022学年度人教版九年级数学上册新考向多视角同步训练(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十二章
二次函数
22.1
二次函数的图像和性质
22.1.4
二次函数y=ax2+bx+c的图像和性质
知识能力全练
知识点一
二次函数y=ax2+bx+c的图象和性质
1.(2021广东广州越秀期中)下列对二次函数y=x2-x的图象的描述,正确的是
(
)
A开口向下
B.对称轴是y轴
C.顶点坐标为
eq
\b
\bc\((,-)
D.在对称轴右侧,y随x的增大而减小
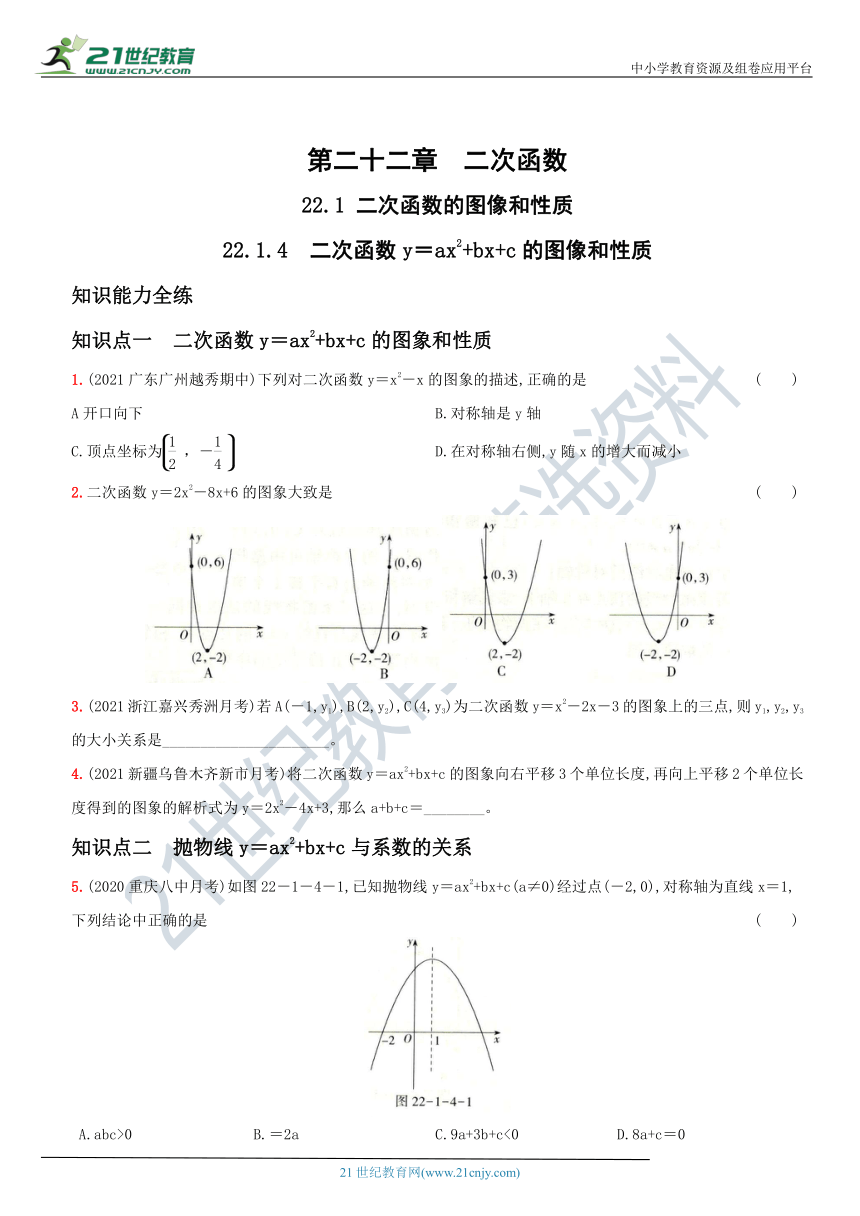
2.二次函数y=2x2-8x+6的图象大致是
(
)
3.(2021浙江嘉兴秀洲月考)若A(-1,y1),B(2,y2),C(4,y3)为二次函数y=x2-2x-3的图象上的三点,则y1,y2,y3的大小关系是______________________。
4.(2021新疆乌鲁木齐新市月考)将二次函数y=ax2+bx+c的图象向右平移3个单位长度,再向上平移2个单位长度得到的图象的解析式为y=2x2-4x+3,那么a+b+c=________。
知识点二
抛物线y=ax2+bx+c与系数的关系
5.(2020重庆八中月考)如图22-1-4-1,已知抛物线y=ax2+bx+c(a≠0)经过点(-2,0),对称轴为直线x=1,下列结论中正确的是
(
)
A.abc>0
B.=2a
C.9a+3b+c<0
D.8a+c=0
6.(2021独家原创试题)已知二次函数y=ax2+bx+c的图象如图22-1-4-2所示,则点P(ab+c,abc)在第________象限.
知识点三
待定系数法求二次函数解析式
7.(2020天津和平期中)若抛物线的顶点为(1,-4),与y轴交于点(0,-3),则该抛物线的解析式为
(
)
A.y=x2-2x-3
B.y=x2+2x-3
C.y=x2-2x+3
D.y=2x2-3x-3
8.(2021安徽合肥庐阳月考)已知抛物线与二次函数y=-5x2的图象的形状相同,开口方向相同,且顶点坐标为(-1,2020),它对应的函数表达式为
(
)
A.y=-5(x-1)2+2020
B.y=5(x-1)2+2020
C.y=5(x+1)2+2020
D.y=-5(x+1)2+2020
9.(2020辽宁大连甘井子期末)已知抛物线的对称轴是y轴,且经过点(1,3)、(2,6),则该抛物线的解析式为________
10.(2017广西百色中考)经过A(4,0),B(-2,0),C(0,3)三点的抛物线的解析式是________________。
11.(2021北京东城期中)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
根据上表,回答下列问题:
(1)直接写出c,m的值;
(2)求此二次函数的解析式
三年模拟全练
12.(2021山东临沂沂南期中,11,★★☆)已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
下列结论正确的是
(
)
A.抛物线的开口向下
B.抛物线的对称轴为直线x=2
C.当0≤x≤4时,y≥0
D.若点(x1,2),(x2,3)在该抛物线上,则x113.(2021天津南开实验中学期末,10,★★☆)已知二次函数y=x2-(m-2)x+4的图象的顶点在坐标轴上,则m的值一定不是
(
)
A.2
B.6
C.-2
D.0
14.(2021福建厦门思明月考,15,★★☆)已知y是x的二次函数,y与x的部分对应值如下表:
则该二次函数图象向左平移________个单位后,图象经过原点.
五年中考全练
15.(2019重庆中考,5,★☆☆)抛物线y=-3x2+6x+2的对称轴是
(
)
A.直线x=2
B.直线x=-2
C.直线x=1
D.直线x=-1
16.(2020浙江温州中考,9,★★☆)已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则
(
)
A.y3B.y3C.y2D.y117.(2020山东菏泽中考,8,★★☆)一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象
可能是
(
)
18.(2020河北中考,15,★★☆)如图22-1-4-3,现要在抛物线y=x(4-x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若b=5,则点P的个数为0;
乙:若b=4,则点P的个数为1;
丙:若b=3,则点P的个数为1
下列判断正确的是
(
)
A.乙错,丙对
B.甲和乙都错
C.乙对,丙错
D.甲错,丙对
19.(2020广西贵港中考,18,★★☆)如图22-1-4-4,对于抛物线y1=-x2+x+1,y2=-x2+2x+1,y3=-x2+3x+1,给出下列结论:①这三条抛物线都经过点C(0,1);②抛物线y3的对称轴可由抛物线y1的对称轴向右平移1个单位而得到;③这三条抛物线的顶点在同一条直线上;④这三条抛物线与直线y=1的交点中,相邻两点之间的距离相等其中正确结论的序号是________
20.(2020山东临沂中考,25,★★☆)已知抛物线y=ax2-2ax-3+2a2(a≠0)
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其解析式;
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1核心素养全练
21.(2019湖北武汉硚口月考)抛物线y=x2+mx+m+经过定点的坐标是________.
22.(2021独家原创试题)如图22-1-4-5,在平面直角坐标系中,二次函数y=-x2+2x+2的图象与x轴、y轴分别交于A、B、C三点,点D是其顶点,若点P是x轴上一个动点,则CP+DP的最小值为________
????????????????????????????????????????????????????????????
《参考答案及解析》
22.1.4
二次函数y=ax2+bx+c的图象和性质
知识能力全练
1.C
∵y=x2-x=
eq
\b
\bc\((
x-)
-,∴图象开口向上,故A错误;对称轴是直线x=,故B错误;顶点坐标为(,),故C正确;在对称轴右侧,y随x的增大而增大,故D错误.故选C.
2.A
y=x2-8x+6=2(x-2)2-2,即抛物线的顶点坐标为(2,-2),令x=0,则y=6,即抛物线过点(0,6).故选A.
3.【答案】y2【解析】∵图象的开口向上,对称轴是直线x==1,∴A(-1,y1)关于直线x=1的对称点是(3,y1)∵1<2<3<4,∴y24.【答案】17
【解析】y=2x2-4x+3=2(x-1)2+1,把抛物线y=2(x-1)2+1向左平移3个单位长度,向下平移2个单位长度得到的抛物线的解析式为y=2(x-1+3)2+1-2=2x2+8x+7,所以a=2,b=8,c=7,所以a+b+c=17.
5.D
∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a>0,故B错误;∵抛物线与y轴的正半轴相交,∴c>0,∴abc<0,故A错误;∵对称轴为直线x=1,又点(-2,0)关于直线x=1的对称点的坐标为(4,0),∴当x=3时y=9a+3b+c>0,故C错误∵抛物线y=ax2+bx+c经过点(-2,0),4a-2b+c=0,∵b=-2a,∴4a+4a+c=0,即8a+c=0,故D正确.故选D
6.【答案】一
【解析】∵抛物线开口向下,∴a<0;∵对称轴在y轴左侧,∴ab>0;∵图象与y轴的交点在正半轴上,∴c>0,∴b+c>0,abc>0,∴点P(ab+c,abc)在第一象限
7.A
设抛物线的解析式为y=a(x-1)2-4,将(0,-3)代入y=a(x-1)2-4,得-3=a(0-1)2-4,解得a=1,∴抛物线的解析式为y=(x-1)2-4=x2-2x-3.故选A.
8.D
∵顶点坐标为(-1,2020),∴设抛物线的解析式为y=a(x+1)2+2020,∵与二次函数y=-5x2的图象的形状相同,开口方向相同,∴a=-5,∴抛物线的解析式为y=-5(x+1)2+2020.故选D.
9.【答案】y=x2+2
【解析】∵抛物线的对称轴是y轴,∴设此抛物线的解析式是y=ax2+c,把点(1,3)、(2,6)代入得,解得a=1,c=2,则此抛物线的解析式是y=x2+2.
10.【答案】y=-x2+x+3
【解析】解法一:设抛物线的解析式为y=ax2+bx+c(a≠0),把A(4,0),B(-2,0),C(0,3)代入得,解得
eq
\b
\lc\{(\a
\al
\co1(a=-,
b=,c=3))
,∴抛物线的解析式为y=-x2+x+3
解法二:设抛物线的解析式为y=a(x+2)(x-4),把C(0,3)代入得-8a=3,即a=-,则抛物线的解析式为y=-(x+2)(x-4)=-x2+x+3
11.【解析】(1)c=4,m=
(2)由表格可知,图象顶点为
eq
\b
\bc\((-1,)
设y=a(x+1)2+,
将(0,4)代入y=a(x+1)2+得,a+=4,解得a=-,
∴这个二次函数的解析式为y=-(x+1)2+
三年模拟全练
12.B
由表格可得,抛物线的对称轴为直线x==2,故B正确;抛物线的顶点坐标为(2,-4),且抛物线与x轴相交,开口向上,故A错误;当0≤x≤4时,y≤0,故C错误;由二次函数图象具有对称性可知,若点(x1,2),(x2,3)在抛物线上,则x113.D
∵y=x2-(m-2)x+4=
eq
\b
\bc\((
x-)
eq
\s\up7(2)
-+4,∴该函数的顶点坐标为
eq
\b
\bc\((,-+4)
∵二次函数y=x2-(m-2)x+4的图象的顶点在坐标轴上,
∴=0或-+4=0,解得m=2或m=-2或m=6.故选D.
14.【答案】3
【解析】由表格得,二次函数图象的对称轴是直线x==,∵抛物线与x轴的一个交点为(-2,0),∴该抛物线与x轴的另一个交点为(3,0),∴该二次函数图象向左平移3个单位后,图象经过原点
五年中考全练
15.c
对称轴为x==1.故选C.
16.B
抛物线的对称轴为直线x==-2,∵a=-3<0,∴抛物线开口向下,∴x=-2时,函数值最大,又∵直线x=-3到直线x=-2的距离比直线x=1到直线x=-2的距离小,∴y317.B
选项A,由抛物线可知,a>0,b<0,c>0则ac>0,由直线可知,ac>0,b>0,故A错误;选项B,由抛物线可知,a〉0,b>0,c>0,则ac>0,由直线可知,ac>0,b>0,故B正确;选项C,由抛物线可知,a<0,b>0,c0,则ac<0,由直线可知,ac<0,b<0,故C错误;选项D,由抛物线可知,a<0,b<0,c>0,则ac<0,由直线可知,ac>0,b>0,故D错误故选B.
18.C
y=x(4-x)=-x2+4x=-(x-2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为,可知甲、乙的说法正确;∵抛物线上纵坐标为3的点有2个,∴丙的说法不正确.故选C
19.【答案】①②④
【解析】①将x=0分别代入抛物线的解析式,可得y1=y2=y3=1,①正确;②抛物线y1=-x2+x+1,y3=-x2+3x+1的对称轴分别为直线x=,x=,由x=,向右平移1个单位得到x=,②正确;③y1=-x2+x+1=-
eq
\b
\bc\((
x-)
eq
\s\up7(2)
+,其顶点坐标为
eq
\b
\bc\((,
)
;y2=-x2+2x+1=-(x-1)2+2,其顶点坐标为(1,2);y3=-x2+3x+1=-
eq
\b
\bc\((
x-)
eq
\s\up7(2)
+,其顶点坐标为
eq
\b
\bc\((,)
,可知三条抛物线的顶点不在同一条直线上,③错误;④当y=1时,-x2+x+1=1,∴x=0或x=1;-x2+2x+1=1,∴x=0或x=2;-x2+3x+1=1,∴x=0或x=3,∴三条抛物线与直线y=1的交点中,相邻两点之间的距离都是1,④正确.故答案为①②④.
20.【解析】(1)∵抛物线y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3,
∴抛物线的对称轴为直线x=1
(2)∵抛物线的顶点在x轴上,
∴2a2-a-3=0
解得a=或a=-1,
∴抛物线为y=x2-3x+或y=-x2+2x-1.
(3)抛物线的对称轴为x=1,
Q(3,y2)关于直线x=1的对称点的坐标为(-1,y2)
当a>0时,要使y13.
核心素养全练
21.【答案】(-1,1)
【解析】∵y=x2+(x+1)m+,抛物线经过定点,
∴x+1=0,∴x=-1,∴y=1,∴定点坐标为(-1,1).
22.【答案】2
【解析】如图,作DE⊥y轴于点E,取点C关于x轴的对称点C′,连接
C′D,则C′D的长就是CP+DP的最小值.把x=0代入y=-x2+2x+
2,得y=2,∴C(0,2),∴C′(0,-2)∵y=-x2+2x+2=-
(x-2)2
+4,∴点D(2,4),E(0,4),∴DE=2,C′E=6.在Rt△C′DE中,C′
D=
=2,即CP+DP的最小值为2.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第二十二章
二次函数
22.1
二次函数的图像和性质
22.1.4
二次函数y=ax2+bx+c的图像和性质
知识能力全练
知识点一
二次函数y=ax2+bx+c的图象和性质
1.(2021广东广州越秀期中)下列对二次函数y=x2-x的图象的描述,正确的是
(
)
A开口向下
B.对称轴是y轴
C.顶点坐标为
eq
\b
\bc\((,-)
D.在对称轴右侧,y随x的增大而减小
2.二次函数y=2x2-8x+6的图象大致是
(
)
3.(2021浙江嘉兴秀洲月考)若A(-1,y1),B(2,y2),C(4,y3)为二次函数y=x2-2x-3的图象上的三点,则y1,y2,y3的大小关系是______________________。
4.(2021新疆乌鲁木齐新市月考)将二次函数y=ax2+bx+c的图象向右平移3个单位长度,再向上平移2个单位长度得到的图象的解析式为y=2x2-4x+3,那么a+b+c=________。
知识点二
抛物线y=ax2+bx+c与系数的关系
5.(2020重庆八中月考)如图22-1-4-1,已知抛物线y=ax2+bx+c(a≠0)经过点(-2,0),对称轴为直线x=1,下列结论中正确的是
(
)
A.abc>0
B.=2a
C.9a+3b+c<0
D.8a+c=0
6.(2021独家原创试题)已知二次函数y=ax2+bx+c的图象如图22-1-4-2所示,则点P(ab+c,abc)在第________象限.
知识点三
待定系数法求二次函数解析式
7.(2020天津和平期中)若抛物线的顶点为(1,-4),与y轴交于点(0,-3),则该抛物线的解析式为
(
)
A.y=x2-2x-3
B.y=x2+2x-3
C.y=x2-2x+3
D.y=2x2-3x-3
8.(2021安徽合肥庐阳月考)已知抛物线与二次函数y=-5x2的图象的形状相同,开口方向相同,且顶点坐标为(-1,2020),它对应的函数表达式为
(
)
A.y=-5(x-1)2+2020
B.y=5(x-1)2+2020
C.y=5(x+1)2+2020
D.y=-5(x+1)2+2020
9.(2020辽宁大连甘井子期末)已知抛物线的对称轴是y轴,且经过点(1,3)、(2,6),则该抛物线的解析式为________
10.(2017广西百色中考)经过A(4,0),B(-2,0),C(0,3)三点的抛物线的解析式是________________。
11.(2021北京东城期中)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
根据上表,回答下列问题:
(1)直接写出c,m的值;
(2)求此二次函数的解析式
三年模拟全练
12.(2021山东临沂沂南期中,11,★★☆)已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表:
下列结论正确的是
(
)
A.抛物线的开口向下
B.抛物线的对称轴为直线x=2
C.当0≤x≤4时,y≥0
D.若点(x1,2),(x2,3)在该抛物线上,则x1
(
)
A.2
B.6
C.-2
D.0
14.(2021福建厦门思明月考,15,★★☆)已知y是x的二次函数,y与x的部分对应值如下表:
则该二次函数图象向左平移________个单位后,图象经过原点.
五年中考全练
15.(2019重庆中考,5,★☆☆)抛物线y=-3x2+6x+2的对称轴是
(
)
A.直线x=2
B.直线x=-2
C.直线x=1
D.直线x=-1
16.(2020浙江温州中考,9,★★☆)已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则
(
)
A.y3
可能是
(
)
18.(2020河北中考,15,★★☆)如图22-1-4-3,现要在抛物线y=x(4-x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若b=5,则点P的个数为0;
乙:若b=4,则点P的个数为1;
丙:若b=3,则点P的个数为1
下列判断正确的是
(
)
A.乙错,丙对
B.甲和乙都错
C.乙对,丙错
D.甲错,丙对
19.(2020广西贵港中考,18,★★☆)如图22-1-4-4,对于抛物线y1=-x2+x+1,y2=-x2+2x+1,y3=-x2+3x+1,给出下列结论:①这三条抛物线都经过点C(0,1);②抛物线y3的对称轴可由抛物线y1的对称轴向右平移1个单位而得到;③这三条抛物线的顶点在同一条直线上;④这三条抛物线与直线y=1的交点中,相邻两点之间的距离相等其中正确结论的序号是________
20.(2020山东临沂中考,25,★★☆)已知抛物线y=ax2-2ax-3+2a2(a≠0)
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其解析式;
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1
21.(2019湖北武汉硚口月考)抛物线y=x2+mx+m+经过定点的坐标是________.
22.(2021独家原创试题)如图22-1-4-5,在平面直角坐标系中,二次函数y=-x2+2x+2的图象与x轴、y轴分别交于A、B、C三点,点D是其顶点,若点P是x轴上一个动点,则CP+DP的最小值为________
????????????????????????????????????????????????????????????
《参考答案及解析》
22.1.4
二次函数y=ax2+bx+c的图象和性质
知识能力全练
1.C
∵y=x2-x=
eq
\b
\bc\((
x-)
-,∴图象开口向上,故A错误;对称轴是直线x=,故B错误;顶点坐标为(,),故C正确;在对称轴右侧,y随x的增大而增大,故D错误.故选C.
2.A
y=x2-8x+6=2(x-2)2-2,即抛物线的顶点坐标为(2,-2),令x=0,则y=6,即抛物线过点(0,6).故选A.
3.【答案】y2
【解析】y=2x2-4x+3=2(x-1)2+1,把抛物线y=2(x-1)2+1向左平移3个单位长度,向下平移2个单位长度得到的抛物线的解析式为y=2(x-1+3)2+1-2=2x2+8x+7,所以a=2,b=8,c=7,所以a+b+c=17.
5.D
∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a>0,故B错误;∵抛物线与y轴的正半轴相交,∴c>0,∴abc<0,故A错误;∵对称轴为直线x=1,又点(-2,0)关于直线x=1的对称点的坐标为(4,0),∴当x=3时y=9a+3b+c>0,故C错误∵抛物线y=ax2+bx+c经过点(-2,0),4a-2b+c=0,∵b=-2a,∴4a+4a+c=0,即8a+c=0,故D正确.故选D
6.【答案】一
【解析】∵抛物线开口向下,∴a<0;∵对称轴在y轴左侧,∴ab>0;∵图象与y轴的交点在正半轴上,∴c>0,∴b+c>0,abc>0,∴点P(ab+c,abc)在第一象限
7.A
设抛物线的解析式为y=a(x-1)2-4,将(0,-3)代入y=a(x-1)2-4,得-3=a(0-1)2-4,解得a=1,∴抛物线的解析式为y=(x-1)2-4=x2-2x-3.故选A.
8.D
∵顶点坐标为(-1,2020),∴设抛物线的解析式为y=a(x+1)2+2020,∵与二次函数y=-5x2的图象的形状相同,开口方向相同,∴a=-5,∴抛物线的解析式为y=-5(x+1)2+2020.故选D.
9.【答案】y=x2+2
【解析】∵抛物线的对称轴是y轴,∴设此抛物线的解析式是y=ax2+c,把点(1,3)、(2,6)代入得,解得a=1,c=2,则此抛物线的解析式是y=x2+2.
10.【答案】y=-x2+x+3
【解析】解法一:设抛物线的解析式为y=ax2+bx+c(a≠0),把A(4,0),B(-2,0),C(0,3)代入得,解得
eq
\b
\lc\{(\a
\al
\co1(a=-,
b=,c=3))
,∴抛物线的解析式为y=-x2+x+3
解法二:设抛物线的解析式为y=a(x+2)(x-4),把C(0,3)代入得-8a=3,即a=-,则抛物线的解析式为y=-(x+2)(x-4)=-x2+x+3
11.【解析】(1)c=4,m=
(2)由表格可知,图象顶点为
eq
\b
\bc\((-1,)
设y=a(x+1)2+,
将(0,4)代入y=a(x+1)2+得,a+=4,解得a=-,
∴这个二次函数的解析式为y=-(x+1)2+
三年模拟全练
12.B
由表格可得,抛物线的对称轴为直线x==2,故B正确;抛物线的顶点坐标为(2,-4),且抛物线与x轴相交,开口向上,故A错误;当0≤x≤4时,y≤0,故C错误;由二次函数图象具有对称性可知,若点(x1,2),(x2,3)在抛物线上,则x1
∵y=x2-(m-2)x+4=
eq
\b
\bc\((
x-)
eq
\s\up7(2)
-+4,∴该函数的顶点坐标为
eq
\b
\bc\((,-+4)
∵二次函数y=x2-(m-2)x+4的图象的顶点在坐标轴上,
∴=0或-+4=0,解得m=2或m=-2或m=6.故选D.
14.【答案】3
【解析】由表格得,二次函数图象的对称轴是直线x==,∵抛物线与x轴的一个交点为(-2,0),∴该抛物线与x轴的另一个交点为(3,0),∴该二次函数图象向左平移3个单位后,图象经过原点
五年中考全练
15.c
对称轴为x==1.故选C.
16.B
抛物线的对称轴为直线x==-2,∵a=-3<0,∴抛物线开口向下,∴x=-2时,函数值最大,又∵直线x=-3到直线x=-2的距离比直线x=1到直线x=-2的距离小,∴y3
选项A,由抛物线可知,a>0,b<0,c>0则ac>0,由直线可知,ac>0,b>0,故A错误;选项B,由抛物线可知,a〉0,b>0,c>0,则ac>0,由直线可知,ac>0,b>0,故B正确;选项C,由抛物线可知,a<0,b>0,c0,则ac<0,由直线可知,ac<0,b<0,故C错误;选项D,由抛物线可知,a<0,b<0,c>0,则ac<0,由直线可知,ac>0,b>0,故D错误故选B.
18.C
y=x(4-x)=-x2+4x=-(x-2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为,可知甲、乙的说法正确;∵抛物线上纵坐标为3的点有2个,∴丙的说法不正确.故选C
19.【答案】①②④
【解析】①将x=0分别代入抛物线的解析式,可得y1=y2=y3=1,①正确;②抛物线y1=-x2+x+1,y3=-x2+3x+1的对称轴分别为直线x=,x=,由x=,向右平移1个单位得到x=,②正确;③y1=-x2+x+1=-
eq
\b
\bc\((
x-)
eq
\s\up7(2)
+,其顶点坐标为
eq
\b
\bc\((,
)
;y2=-x2+2x+1=-(x-1)2+2,其顶点坐标为(1,2);y3=-x2+3x+1=-
eq
\b
\bc\((
x-)
eq
\s\up7(2)
+,其顶点坐标为
eq
\b
\bc\((,)
,可知三条抛物线的顶点不在同一条直线上,③错误;④当y=1时,-x2+x+1=1,∴x=0或x=1;-x2+2x+1=1,∴x=0或x=2;-x2+3x+1=1,∴x=0或x=3,∴三条抛物线与直线y=1的交点中,相邻两点之间的距离都是1,④正确.故答案为①②④.
20.【解析】(1)∵抛物线y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3,
∴抛物线的对称轴为直线x=1
(2)∵抛物线的顶点在x轴上,
∴2a2-a-3=0
解得a=或a=-1,
∴抛物线为y=x2-3x+或y=-x2+2x-1.
(3)抛物线的对称轴为x=1,
Q(3,y2)关于直线x=1的对称点的坐标为(-1,y2)
当a>0时,要使y1
核心素养全练
21.【答案】(-1,1)
【解析】∵y=x2+(x+1)m+,抛物线经过定点,
∴x+1=0,∴x=-1,∴y=1,∴定点坐标为(-1,1).
22.【答案】2
【解析】如图,作DE⊥y轴于点E,取点C关于x轴的对称点C′,连接
C′D,则C′D的长就是CP+DP的最小值.把x=0代入y=-x2+2x+
2,得y=2,∴C(0,2),∴C′(0,-2)∵y=-x2+2x+2=-
(x-2)2
+4,∴点D(2,4),E(0,4),∴DE=2,C′E=6.在Rt△C′DE中,C′
D=
=2,即CP+DP的最小值为2.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
