22.2 二次函数与一元二次方程-2021至2022学年度人教版九年级数学上册新考向多视角同步训练(含解析)
文档属性
| 名称 | 22.2 二次函数与一元二次方程-2021至2022学年度人教版九年级数学上册新考向多视角同步训练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 10:06:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十二章
二次函数
22.2
二次函数与一元二次方程
知识能力全练
知识点一
二次函数与一元二次方程的关系
1.(2021广西河池环江期中)抛物线y=x2+bx+c如图22-2-1所示,则关于x的方程x2+bx+c=0的解是
(
)
A.无解
B.x=1
C.x=-4
D.x1=-1,x2=4
2.(2020浙江绍兴诸暨期中)抛物线y=x2-6x+9与坐标轴的交点个数是
(
)
A.0
B.1
C.2
D.3
3.(2021福建厦门思明期中)已知二次函数y=(x-p)(x-q)-2,若m,n是关于x的方程(x-p)(x-q)-2=0的两个根,则实数m,n,p,q的大小关系可能是
(
)
A.mB.mC.pD.p4.(2021湖北十堰丹江口期中)抛物线y=ax2+bx+c经过A(-3,0),B(1,0)两点,则关于x的一元二次方程ax2+bx+c=0的解是________。
5.(2021安徽淮南崇文中学月考)如果抛物线y=x2-2x+m与x轴有公共点,则m的取值范围是________
6.(2020江苏徐州睢宁期中)二次函数y=2(x-1)(x+5)的图象与x轴的两个交点之间的距离是________
知识点二
利用二次函数y=ax2+bx+c的图象解不等式
7.(2020四川绵阳涪城月考)二次函数y=ax2+bx+c的部分对应值如下表:
利用二次函数的图象可知,当函数值y<0时,x的取值范围是
(
)
A.x<0或x>2
B.0C.x<-1或x>3
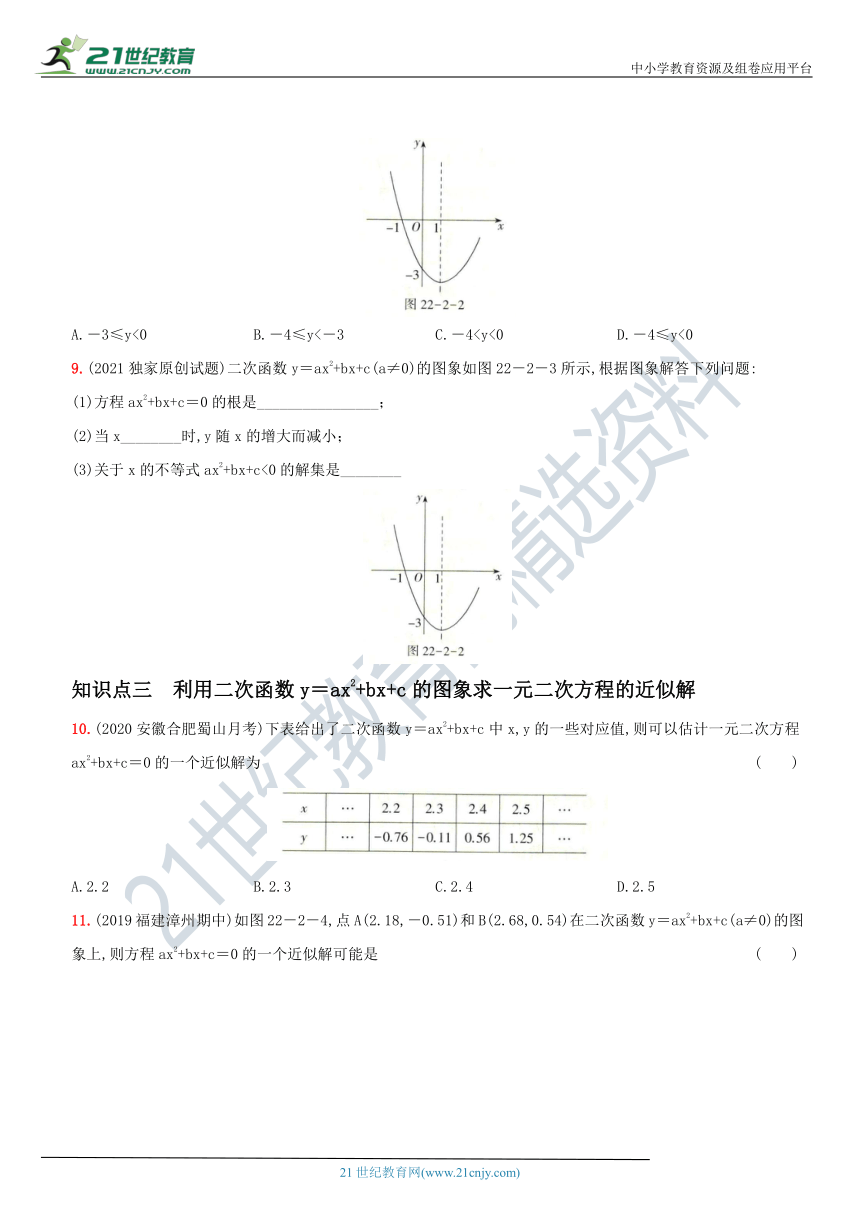
D.-18.(2020河南洛阳期中)已知二次函数y=x2+bx+c的部分图象如图22-2-2所示,若-1(
)
A.-3≤y<0
b.-4≤y<-3
C.-4D.-4≤y<0
9.(2021独家原创试题)二次函数y=ax2+bx+c(a≠0)的图象如图22-2-3所示,根据图象解答下列问题:
(1)方程ax2+bx+c=0的根是________________;
(2)当x________时,y随x的增大而减小;
(3)关于x的不等式ax2+bx+c<0的解集是________
知识点三
利用二次函数y=ax2+bx+c的图象求一元二次方程的近似解
10.(2020安徽合肥蜀山月考)下表给出了二次函数y=ax2+bx+c中x,y的一些对应值,则可以估计一元二次方程ax2+bx+c=0的一个近似解为
(
)
A.2.2
B.2.3
C.2.4
D.2.5
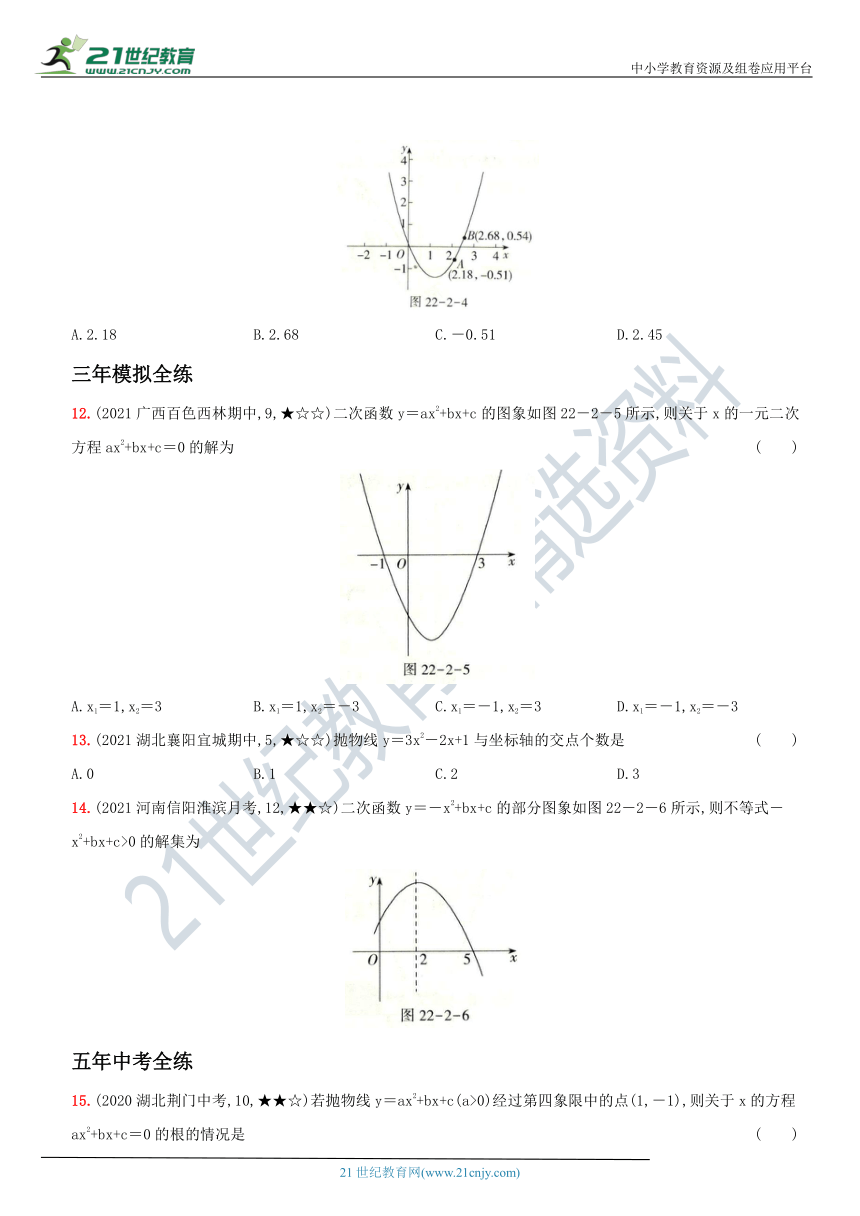
11.(2019福建漳州期中)如图22-2-4,点A(2.18,-0.51)和B(2.68,0.54)在二次函数y=ax2+bx+c(a≠0)的图象上,则方程ax2+bx+c=0的一个近似解可能是
(
)
A.2.18
B.2.68
C.-0.51
D.2.45
三年模拟全练
12.(2021广西百色西林期中,9,★☆☆)二次函数y=ax2+bx+c的图象如图22-2-5所示,则关于x的一元二次方程ax2+bx+c=0的解为
(
)
A.x1=1,x2=3
B.x1=1,x2=-3
C.x1=-1,x2=3
D.x1=-1,x2=-3
13.(2021湖北襄阳宜城期中,5,★☆☆)抛物线y=3x2-2x+1与坐标轴的交点个数是
(
)
A.0
B.1
C.2
D.3
14.(2021河南信阳淮滨月考,12,★★☆)二次函数y=-x2+bx+c的部分图象如图22-2-6所示,则不等式-x2+bx+c>0的解集为
五年中考全练
15.(2020湖北荆门中考,10,★★☆)若抛物线y=ax2+bx+c(a>0)经过第四象限中的点(1,-1),则关于x的方程ax2+bx+c=0的根的情况是
(
)
A.有两个大于1的不相等实数根
B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根
D.没有实数根
16.(2020山东青岛中考,12,★☆☆)抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是________
17.(2019山东济宁中考,15,★★☆)如图22-2-7,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是________________
18.(2019云南中考,21,★★☆)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+-6)x+3k上,且P到y轴的距离是2,求点P的坐标
核心素养全练
19.(2021独家原创试题)已知二次函数y=ax2+bx+c(a≠0)的图象如图22-2-8所示,对称轴为直线x=-1,图象与y轴的交点坐标为(0,-3).若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x2(
)
A.①②
B.①③
C.②③
D.①②③
20.(2018浙江杭州中考)四位同学在研究函数y=x2+bx+c(b,c是常数),甲发现当x=1时,函数有最小值;乙发现-1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4.已知这四位同学中只有一位发现的结论是错误的,则该同学是
(
)
A.甲
B.乙
C.丙
D.丁
????????????????????????????????????????????????????????????
《参考答案及解析》
22.2
二次函数与一元二次方程
知识能力全练
1.D
∵抛物线y=x2+bx+c与x轴交点的横坐标分别是-1、4,∴关于x的方程x2+bx+c=0的解是x1=-1,x2=4.故选D.
2.C
b2-4ac=(-6)2-4×1×9=0,∴二次函数y=x2-6x+9的图象与x轴有1个交点∵抛物线y=x2-6x+9与y轴有1个交点,∴抛物线y=x2-6x+9与坐标轴的交点的个数是2.故选C.
3.A
∵二次函数的解析式为y=(x-p)(x-q)-2,∴该函数图象开口向上,当x=p或x=q时,y=-2,∵m,n是关于x的方程(x-p)(x-q)-2=0的两个根,∴当x=m或x=n时,y=0,画图易知p,q一定处在m,n中间.故选A.
4.【答案】x1=-3,x2=1
【解析】∵抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)两点,∴当x=-3或x=1时,y=0,∴一元二次方程ax2+bx+c=0的解是x1=-3,x2=1
5.【答案】m≤1
【解析】∵抛物线y=x2-2x+m与x轴有公共点,∴(-2)2-4×1xm≥0,解得m≤1.
6.【答案】6
【解析】当y=0时,2(x-1)(x+5)=0,解得x1=1,x2=-5,∴二次函数y=2(x-1)(x+5)的图象与x轴的交点坐标是(1,0),(-5,0),∴两个交点之间的距离是1-(-5)=6
7.D
由表格可知,对称轴为直线x=1,图象开口向上,与x轴交于(-1,0)、(3,0)两点,则当函数值y<0时,x的取值范围是-18.D
∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点坐标为(-1,0),∴抛物线与x轴的另一个交点坐标为(3,0),结合题意知抛物线的解析式为y=(x+1)(x-3)∵y=(x+1)(x-3)=(x-1)2-4,∴x=1时,y有最小值-4,又x=2时,y=(x+1)(x-3)=-3,x=-1时,y=0∴当-19.【解析】(1)x1=1,x2=-3.
(2)<-1.
(3)-310.B
当x=2.3时,y=-0.11;当x=2.4时,y=0.56.∵-0.11更接近于0
∴方程的一个近似解为2.3.故选B.
11.D
∵图象上有两点,分别为A(2.18,-0.51),B(2.68,0.54),∴当x=2.18时,y=-0.51<0;当x=2.68时,y=0.54>0,∴在2.18与2.68之间,必存在一个x值使y=0(此时对应二次函数图象与x轴的一个交点),又∵2.18<2.45<2.68.故选项D符合.由图象可知,二次函数y=ax2+bx+c(a≠0)的图象与x轴的另一个交点在0和1之间,无选项符合.故选D.
三年模拟全练
12.C
抛物线与x轴的交点坐标为(-1,0)、(3,0),则关于x的一元二次方程ax2+bx+c=0的解为x1=-1,x2=3.故选C.
13.B
∵△=(-2)2-4×3×1=-8<0,∴抛物线与x轴没有交点,而抛物线y=3x2-2x+1与y轴的交点为(0,1),∴抛物线y=3x2-2x+1与坐标轴的交点个数为1.故选B.
14.【答案】-1【解析】抛物线的对称轴为直线x=2,而抛物线与x轴的一个交点坐标为(5,0),所以抛物线与x轴的另一个交点坐标为(-1,0),当-10的解集为-1五年中考全练
15.C
由抛物线y=ax2+bx+c(a>0)经过第四象限中的点(1,-1)可知图象开口向上,顶点在第三或第四象限,∴图象与x轴一定有两个交点,这两个交点分别在(1,0)的左右两边,关于x的方程ax2+bx+c=0有一个大于1另一个小于1的实数根.故选C.
16.【答案】2
【解析】∵抛物线为y=2x2+2(k-1)x-k(k为常数),∴当y=0时,0=2x2+2(k-1)x-k,
∴△=[2(k-1)]2-4×2×(-k)=4k2+4>0,∴0=2x2+2(k-1)x-k有两个不相等的实数根,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点
17.【答案】x<-3或x>1
【解析】∵抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,∴-m+n=p,3m+n=q,∴抛物线y=ax2+c与直线y=-mx+n交于P(1,p),Q(-3,q)两点,观察图象(如图)可知:当x<-3或x>1时,直线y=-mx+n在抛物线y=ax2+c的下方,∴不等式ax2+mx+c>n的解集为x<-3或x>1.
18.【解析】(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,
∴k2+k-6=0,解得k1=-3,k2=2.
又∵抛物线y=x2+(k2+-6)x+3k与x轴有两个交点,
∴△=02-4×3k>0(或3k<0),∴k<0,∴k=-3
(2)由(1)知抛物线的解析式为y=x2-9
∵点P到y轴的距离是2,∴点P的横坐标为2或-2,
当x=2时,y=-5,
当x=-2时,y=-5.
∴P(2,-5)或P(-2,-5),
因此点P的坐标为(2,-5)或(-2,-5).
核心素养全练
19.A
由题意知x1、x2是抛物线与x轴交点的横坐标∵抛物线的对称轴为直线x=-1,x220.B
假设甲和丙发现的结论正确,则
eq
\b
\lc\{(\a
\al
\co1(-=1,=3))
,
解得∴该函数的解析式为y=x2-2x+4.
当x=-1时,y=x2-2x+4=7≠0,
∴乙发现的结论不正确
当x=2时,y=x2-2x+4=4,∴丁发现的结论正确.
∵四位同学中只有乙发现的结论是错误的,∴假设成立.故选B.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第二十二章
二次函数
22.2
二次函数与一元二次方程
知识能力全练
知识点一
二次函数与一元二次方程的关系
1.(2021广西河池环江期中)抛物线y=x2+bx+c如图22-2-1所示,则关于x的方程x2+bx+c=0的解是
(
)
A.无解
B.x=1
C.x=-4
D.x1=-1,x2=4
2.(2020浙江绍兴诸暨期中)抛物线y=x2-6x+9与坐标轴的交点个数是
(
)
A.0
B.1
C.2
D.3
3.(2021福建厦门思明期中)已知二次函数y=(x-p)(x-q)-2,若m,n是关于x的方程(x-p)(x-q)-2=0的两个根,则实数m,n,p,q的大小关系可能是
(
)
A.m
5.(2021安徽淮南崇文中学月考)如果抛物线y=x2-2x+m与x轴有公共点,则m的取值范围是________
6.(2020江苏徐州睢宁期中)二次函数y=2(x-1)(x+5)的图象与x轴的两个交点之间的距离是________
知识点二
利用二次函数y=ax2+bx+c的图象解不等式
7.(2020四川绵阳涪城月考)二次函数y=ax2+bx+c的部分对应值如下表:
利用二次函数的图象可知,当函数值y<0时,x的取值范围是
(
)
A.x<0或x>2
B.0
D.-1
)
A.-3≤y<0
b.-4≤y<-3
C.-4
9.(2021独家原创试题)二次函数y=ax2+bx+c(a≠0)的图象如图22-2-3所示,根据图象解答下列问题:
(1)方程ax2+bx+c=0的根是________________;
(2)当x________时,y随x的增大而减小;
(3)关于x的不等式ax2+bx+c<0的解集是________
知识点三
利用二次函数y=ax2+bx+c的图象求一元二次方程的近似解
10.(2020安徽合肥蜀山月考)下表给出了二次函数y=ax2+bx+c中x,y的一些对应值,则可以估计一元二次方程ax2+bx+c=0的一个近似解为
(
)
A.2.2
B.2.3
C.2.4
D.2.5
11.(2019福建漳州期中)如图22-2-4,点A(2.18,-0.51)和B(2.68,0.54)在二次函数y=ax2+bx+c(a≠0)的图象上,则方程ax2+bx+c=0的一个近似解可能是
(
)
A.2.18
B.2.68
C.-0.51
D.2.45
三年模拟全练
12.(2021广西百色西林期中,9,★☆☆)二次函数y=ax2+bx+c的图象如图22-2-5所示,则关于x的一元二次方程ax2+bx+c=0的解为
(
)
A.x1=1,x2=3
B.x1=1,x2=-3
C.x1=-1,x2=3
D.x1=-1,x2=-3
13.(2021湖北襄阳宜城期中,5,★☆☆)抛物线y=3x2-2x+1与坐标轴的交点个数是
(
)
A.0
B.1
C.2
D.3
14.(2021河南信阳淮滨月考,12,★★☆)二次函数y=-x2+bx+c的部分图象如图22-2-6所示,则不等式-x2+bx+c>0的解集为
五年中考全练
15.(2020湖北荆门中考,10,★★☆)若抛物线y=ax2+bx+c(a>0)经过第四象限中的点(1,-1),则关于x的方程ax2+bx+c=0的根的情况是
(
)
A.有两个大于1的不相等实数根
B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根
D.没有实数根
16.(2020山东青岛中考,12,★☆☆)抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是________
17.(2019山东济宁中考,15,★★☆)如图22-2-7,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集是________________
18.(2019云南中考,21,★★☆)已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+-6)x+3k上,且P到y轴的距离是2,求点P的坐标
核心素养全练
19.(2021独家原创试题)已知二次函数y=ax2+bx+c(a≠0)的图象如图22-2-8所示,对称轴为直线x=-1,图象与y轴的交点坐标为(0,-3).若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x2
)
A.①②
B.①③
C.②③
D.①②③
20.(2018浙江杭州中考)四位同学在研究函数y=x2+bx+c(b,c是常数),甲发现当x=1时,函数有最小值;乙发现-1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4.已知这四位同学中只有一位发现的结论是错误的,则该同学是
(
)
A.甲
B.乙
C.丙
D.丁
????????????????????????????????????????????????????????????
《参考答案及解析》
22.2
二次函数与一元二次方程
知识能力全练
1.D
∵抛物线y=x2+bx+c与x轴交点的横坐标分别是-1、4,∴关于x的方程x2+bx+c=0的解是x1=-1,x2=4.故选D.
2.C
b2-4ac=(-6)2-4×1×9=0,∴二次函数y=x2-6x+9的图象与x轴有1个交点∵抛物线y=x2-6x+9与y轴有1个交点,∴抛物线y=x2-6x+9与坐标轴的交点的个数是2.故选C.
3.A
∵二次函数的解析式为y=(x-p)(x-q)-2,∴该函数图象开口向上,当x=p或x=q时,y=-2,∵m,n是关于x的方程(x-p)(x-q)-2=0的两个根,∴当x=m或x=n时,y=0,画图易知p,q一定处在m,n中间.故选A.
4.【答案】x1=-3,x2=1
【解析】∵抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)两点,∴当x=-3或x=1时,y=0,∴一元二次方程ax2+bx+c=0的解是x1=-3,x2=1
5.【答案】m≤1
【解析】∵抛物线y=x2-2x+m与x轴有公共点,∴(-2)2-4×1xm≥0,解得m≤1.
6.【答案】6
【解析】当y=0时,2(x-1)(x+5)=0,解得x1=1,x2=-5,∴二次函数y=2(x-1)(x+5)的图象与x轴的交点坐标是(1,0),(-5,0),∴两个交点之间的距离是1-(-5)=6
7.D
由表格可知,对称轴为直线x=1,图象开口向上,与x轴交于(-1,0)、(3,0)两点,则当函数值y<0时,x的取值范围是-1
∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点坐标为(-1,0),∴抛物线与x轴的另一个交点坐标为(3,0),结合题意知抛物线的解析式为y=(x+1)(x-3)∵y=(x+1)(x-3)=(x-1)2-4,∴x=1时,y有最小值-4,又x=2时,y=(x+1)(x-3)=-3,x=-1时,y=0∴当-1
(2)<-1.
(3)-3
当x=2.3时,y=-0.11;当x=2.4时,y=0.56.∵-0.11更接近于0
∴方程的一个近似解为2.3.故选B.
11.D
∵图象上有两点,分别为A(2.18,-0.51),B(2.68,0.54),∴当x=2.18时,y=-0.51<0;当x=2.68时,y=0.54>0,∴在2.18与2.68之间,必存在一个x值使y=0(此时对应二次函数图象与x轴的一个交点),又∵2.18<2.45<2.68.故选项D符合.由图象可知,二次函数y=ax2+bx+c(a≠0)的图象与x轴的另一个交点在0和1之间,无选项符合.故选D.
三年模拟全练
12.C
抛物线与x轴的交点坐标为(-1,0)、(3,0),则关于x的一元二次方程ax2+bx+c=0的解为x1=-1,x2=3.故选C.
13.B
∵△=(-2)2-4×3×1=-8<0,∴抛物线与x轴没有交点,而抛物线y=3x2-2x+1与y轴的交点为(0,1),∴抛物线y=3x2-2x+1与坐标轴的交点个数为1.故选B.
14.【答案】-1
15.C
由抛物线y=ax2+bx+c(a>0)经过第四象限中的点(1,-1)可知图象开口向上,顶点在第三或第四象限,∴图象与x轴一定有两个交点,这两个交点分别在(1,0)的左右两边,关于x的方程ax2+bx+c=0有一个大于1另一个小于1的实数根.故选C.
16.【答案】2
【解析】∵抛物线为y=2x2+2(k-1)x-k(k为常数),∴当y=0时,0=2x2+2(k-1)x-k,
∴△=[2(k-1)]2-4×2×(-k)=4k2+4>0,∴0=2x2+2(k-1)x-k有两个不相等的实数根,
∴抛物线y=2x2+2(k-1)x-k(k为常数)与x轴有两个交点
17.【答案】x<-3或x>1
【解析】∵抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,∴-m+n=p,3m+n=q,∴抛物线y=ax2+c与直线y=-mx+n交于P(1,p),Q(-3,q)两点,观察图象(如图)可知:当x<-3或x>1时,直线y=-mx+n在抛物线y=ax2+c的下方,∴不等式ax2+mx+c>n的解集为x<-3或x>1.
18.【解析】(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,
∴k2+k-6=0,解得k1=-3,k2=2.
又∵抛物线y=x2+(k2+-6)x+3k与x轴有两个交点,
∴△=02-4×3k>0(或3k<0),∴k<0,∴k=-3
(2)由(1)知抛物线的解析式为y=x2-9
∵点P到y轴的距离是2,∴点P的横坐标为2或-2,
当x=2时,y=-5,
当x=-2时,y=-5.
∴P(2,-5)或P(-2,-5),
因此点P的坐标为(2,-5)或(-2,-5).
核心素养全练
19.A
由题意知x1、x2是抛物线与x轴交点的横坐标∵抛物线的对称轴为直线x=-1,x2
假设甲和丙发现的结论正确,则
eq
\b
\lc\{(\a
\al
\co1(-=1,=3))
,
解得∴该函数的解析式为y=x2-2x+4.
当x=-1时,y=x2-2x+4=7≠0,
∴乙发现的结论不正确
当x=2时,y=x2-2x+4=4,∴丁发现的结论正确.
∵四位同学中只有乙发现的结论是错误的,∴假设成立.故选B.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
