4.1 几何图形 课堂同步训练 2021-2022学年人教版七年级数学上册(Word版 含答案)
文档属性
| 名称 | 4.1 几何图形 课堂同步训练 2021-2022学年人教版七年级数学上册(Word版 含答案) | 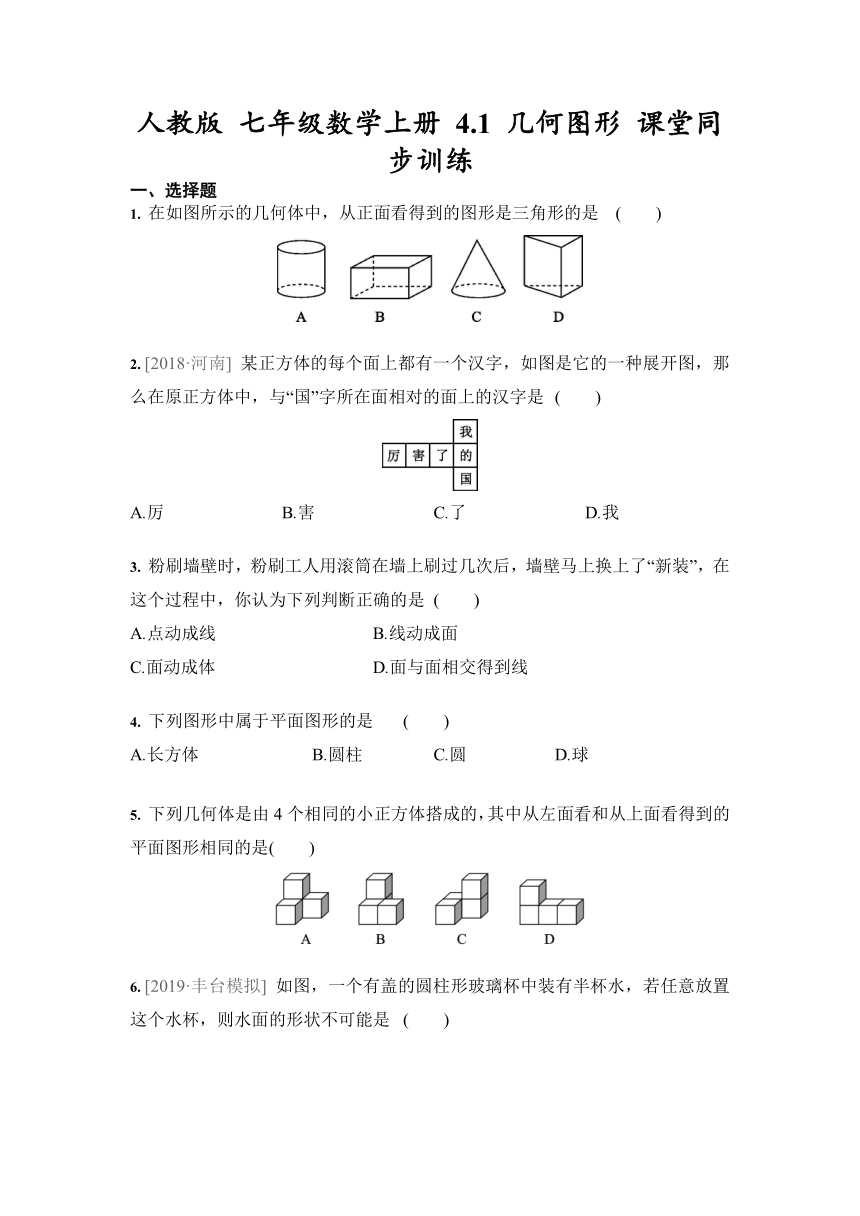 | |
| 格式 | doc | ||
| 文件大小 | 529.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 13:30:57 | ||
图片预览


文档简介
人教版 七年级数学上册 4.1 几何图形 课堂同步训练
一、选择题
1. 在如图所示的几何体中,从正面看得到的图形是三角形的是 ( )
2. [2018·河南] 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是 ( )
A.厉 B.害 C.了 D.我
3. 粉刷墙壁时,粉刷工人用滚筒在墙上刷过几次后,墙壁马上换上了“新装”,在这个过程中,你认为下列判断正确的是 ( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得到线
4. 下列图形中属于平面图形的是 ( )
A.长方体 B.圆柱 C.圆 D.球
5. 下列几何体是由4个相同的小正方体搭成的,其中从左面看和从上面看得到的平面图形相同的是( )
6. [2019·丰台模拟] 如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是 ( )
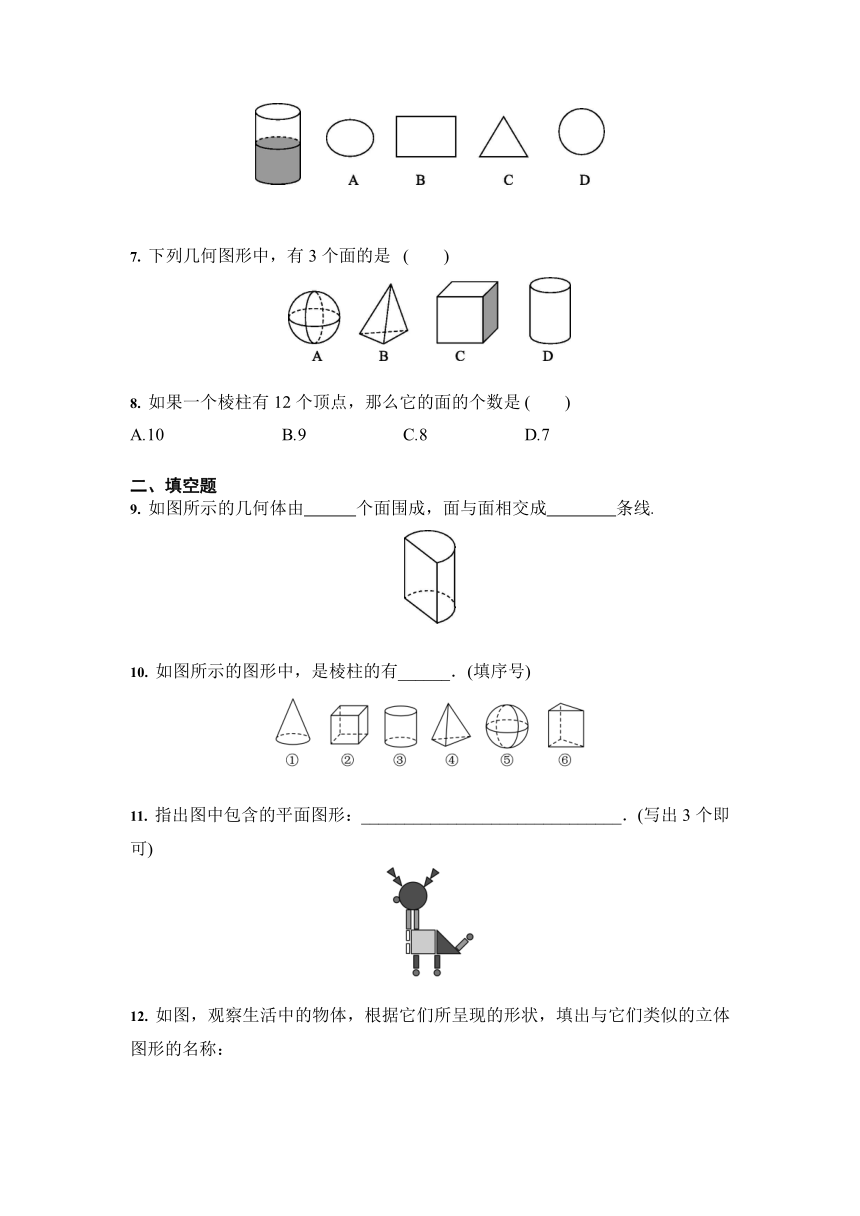
7. 下列几何图形中,有3个面的是 ( )
8. 如果一个棱柱有12个顶点,那么它的面的个数是 ( )
A.10 B.9 C.8 D.7
二、填空题
9. 如图所示的几何体由 个面围成,面与面相交成 条线.?
10. 如图所示的图形中,是棱柱的有______.(填序号)
11. 指出图中包含的平面图形:______________________________.(写出3个即可)
12. 如图,观察生活中的物体,根据它们所呈现的形状,填出与它们类似的立体图形的名称:
(1)______;(2)______;(3)__________;(4)________.
13. 苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是 .?
14. 如图所示的8个立体图形中,是柱体的有 ,是锥体的有 ,是球的有 .(填序号)?
15. 如图所示是某几何体的展开图,那么这个几何体是 .?
16. 如图,把下列实物图和与其对应的立体图形连接起来.
三、解答题
17. 观察图中的圆柱和六棱柱,回答下列问题:
(1)圆柱和六棱柱各由几个面围成?这些面是平的面还是曲的面?
(2)圆柱的侧面与底面相交形成几条线?这些线是直的线还是曲的线?
(3)六棱柱的侧面与下底面相交形成几条线?
(4)六棱柱共有几个顶点?经过一个顶点有几条棱?
18. 如图,下列各几何体的表面中包含哪些平面图形?
19. 十八世纪瑞士数学家欧拉证明了简单多面体的顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面的多面体模型,填写表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 ?
正八面体 ? 8 12
正十二面体 20 12 30
(2)根据上面的表格,猜想顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 (用所给的字母表示);?
(3)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是 ;?
(4)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.
20. 如图①是一张长为4 cm,宽为3 cm的长方形纸片,将该长方形纸片分别绕长、宽所在的直线旋转一周(如图②③),会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大.
21. 如图①是三个直立于水平面上的形状完全相同的几何体(下底面为圆,单位:cm),将它们拼成如图②所示的新几何体,求新几何体的体积(结果保留π).
人教版 七年级数学上册 4.1 几何图形 课堂同步训练-答案
一、选择题
1. 【答案】C [解析] 底面水平放置的圆锥,从正面看得到的平面图形是三角形.
2. 【答案】D
3. 【答案】B
4. 【答案】C
5. 【答案】B
6. 【答案】C
7. 【答案】D
8. 【答案】C [解析] 一个棱柱有12个顶点,一定是六棱柱,所以它有6个侧面和2个底面,共8个面.
二、填空题
9. 【答案】4 6
10. 【答案】②⑥
11. 【答案】圆、三角形、正方形、长方形(答案不唯一,从中任选三个即可)
12. 【答案】(1)圆柱 (2)圆锥 (3)圆柱、圆锥的组合体 (4)球
[解析] 立体图形实际上是由物体抽象得来的.
13. 【答案】观察同一个物体,由于方向和角度不同,看到的图形往往不同
14. 【答案】①②⑤⑦⑧ ④⑥ ③
15. 【答案】圆柱
16. 【答案】①-C,②-B,③-D,④-E,⑤-A 连线略
三、解答题
17. 【答案】
解:(1)圆柱由3个面围成,上、下底面为平的面,侧面为曲的面;六棱柱由8个面围成,这些面都是平的面.
(2)圆柱的侧面与底面相交形成2条线,这些线是曲的线.
(3)六棱柱的侧面与下底面相交形成6条线.
(4)六棱柱共有12个顶点,经过一个顶点有3条棱.
18. 【答案】
(1)长方形 (2)圆 (3)三角形、平行四边形
19. 【答案】
解:(1)观察图形,得长方体的棱数为12,正八面体的顶点数为6.故填6,12.
(2)V+F-E=2
(3)由题意得F+14+F-48=2,解得F=18.
故答案为18.
(4)因为该多面体的顶点数V=24,且每个顶点处有3条棱,
所以该多面体的棱数E==36.
因为V+F-E=2,所以24+x-36=2,
解得x=14.
20. 【答案】
解:绕长方形的长所在的直线旋转一周得到的圆柱的底面半径为3 cm,高为4 cm,体积为π×32×4=36π(cm3).
绕长方形的宽所在的直线旋转一周得到的圆柱的底面半径为4 cm,高为3 cm,体积为π×42×3=48π(cm3).
因此绕长方形的宽所在的直线旋转一周得到的圆柱的体积大.
21. 【答案】
解:π×22×(4+6)+[π×22×(4+6)]=40π+20π=60π(cm3).
答:新几何体的体积为60π cm3.
一、选择题
1. 在如图所示的几何体中,从正面看得到的图形是三角形的是 ( )
2. [2018·河南] 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是 ( )
A.厉 B.害 C.了 D.我
3. 粉刷墙壁时,粉刷工人用滚筒在墙上刷过几次后,墙壁马上换上了“新装”,在这个过程中,你认为下列判断正确的是 ( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得到线
4. 下列图形中属于平面图形的是 ( )
A.长方体 B.圆柱 C.圆 D.球
5. 下列几何体是由4个相同的小正方体搭成的,其中从左面看和从上面看得到的平面图形相同的是( )
6. [2019·丰台模拟] 如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是 ( )
7. 下列几何图形中,有3个面的是 ( )
8. 如果一个棱柱有12个顶点,那么它的面的个数是 ( )
A.10 B.9 C.8 D.7
二、填空题
9. 如图所示的几何体由 个面围成,面与面相交成 条线.?
10. 如图所示的图形中,是棱柱的有______.(填序号)
11. 指出图中包含的平面图形:______________________________.(写出3个即可)
12. 如图,观察生活中的物体,根据它们所呈现的形状,填出与它们类似的立体图形的名称:
(1)______;(2)______;(3)__________;(4)________.
13. 苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是 .?
14. 如图所示的8个立体图形中,是柱体的有 ,是锥体的有 ,是球的有 .(填序号)?
15. 如图所示是某几何体的展开图,那么这个几何体是 .?
16. 如图,把下列实物图和与其对应的立体图形连接起来.
三、解答题
17. 观察图中的圆柱和六棱柱,回答下列问题:
(1)圆柱和六棱柱各由几个面围成?这些面是平的面还是曲的面?
(2)圆柱的侧面与底面相交形成几条线?这些线是直的线还是曲的线?
(3)六棱柱的侧面与下底面相交形成几条线?
(4)六棱柱共有几个顶点?经过一个顶点有几条棱?
18. 如图,下列各几何体的表面中包含哪些平面图形?
19. 十八世纪瑞士数学家欧拉证明了简单多面体的顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面的多面体模型,填写表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 ?
正八面体 ? 8 12
正十二面体 20 12 30
(2)根据上面的表格,猜想顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 (用所给的字母表示);?
(3)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是 ;?
(4)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.
20. 如图①是一张长为4 cm,宽为3 cm的长方形纸片,将该长方形纸片分别绕长、宽所在的直线旋转一周(如图②③),会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大.
21. 如图①是三个直立于水平面上的形状完全相同的几何体(下底面为圆,单位:cm),将它们拼成如图②所示的新几何体,求新几何体的体积(结果保留π).
人教版 七年级数学上册 4.1 几何图形 课堂同步训练-答案
一、选择题
1. 【答案】C [解析] 底面水平放置的圆锥,从正面看得到的平面图形是三角形.
2. 【答案】D
3. 【答案】B
4. 【答案】C
5. 【答案】B
6. 【答案】C
7. 【答案】D
8. 【答案】C [解析] 一个棱柱有12个顶点,一定是六棱柱,所以它有6个侧面和2个底面,共8个面.
二、填空题
9. 【答案】4 6
10. 【答案】②⑥
11. 【答案】圆、三角形、正方形、长方形(答案不唯一,从中任选三个即可)
12. 【答案】(1)圆柱 (2)圆锥 (3)圆柱、圆锥的组合体 (4)球
[解析] 立体图形实际上是由物体抽象得来的.
13. 【答案】观察同一个物体,由于方向和角度不同,看到的图形往往不同
14. 【答案】①②⑤⑦⑧ ④⑥ ③
15. 【答案】圆柱
16. 【答案】①-C,②-B,③-D,④-E,⑤-A 连线略
三、解答题
17. 【答案】
解:(1)圆柱由3个面围成,上、下底面为平的面,侧面为曲的面;六棱柱由8个面围成,这些面都是平的面.
(2)圆柱的侧面与底面相交形成2条线,这些线是曲的线.
(3)六棱柱的侧面与下底面相交形成6条线.
(4)六棱柱共有12个顶点,经过一个顶点有3条棱.
18. 【答案】
(1)长方形 (2)圆 (3)三角形、平行四边形
19. 【答案】
解:(1)观察图形,得长方体的棱数为12,正八面体的顶点数为6.故填6,12.
(2)V+F-E=2
(3)由题意得F+14+F-48=2,解得F=18.
故答案为18.
(4)因为该多面体的顶点数V=24,且每个顶点处有3条棱,
所以该多面体的棱数E==36.
因为V+F-E=2,所以24+x-36=2,
解得x=14.
20. 【答案】
解:绕长方形的长所在的直线旋转一周得到的圆柱的底面半径为3 cm,高为4 cm,体积为π×32×4=36π(cm3).
绕长方形的宽所在的直线旋转一周得到的圆柱的底面半径为4 cm,高为3 cm,体积为π×42×3=48π(cm3).
因此绕长方形的宽所在的直线旋转一周得到的圆柱的体积大.
21. 【答案】
解:π×22×(4+6)+[π×22×(4+6)]=40π+20π=60π(cm3).
答:新几何体的体积为60π cm3.
