12.1全等三角形 同步l练习 2021-2022学年人教版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 12.1全等三角形 同步l练习 2021-2022学年人教版数学八年级上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 00:00:00 | ||
图片预览


文档简介
12.1 全等三角形
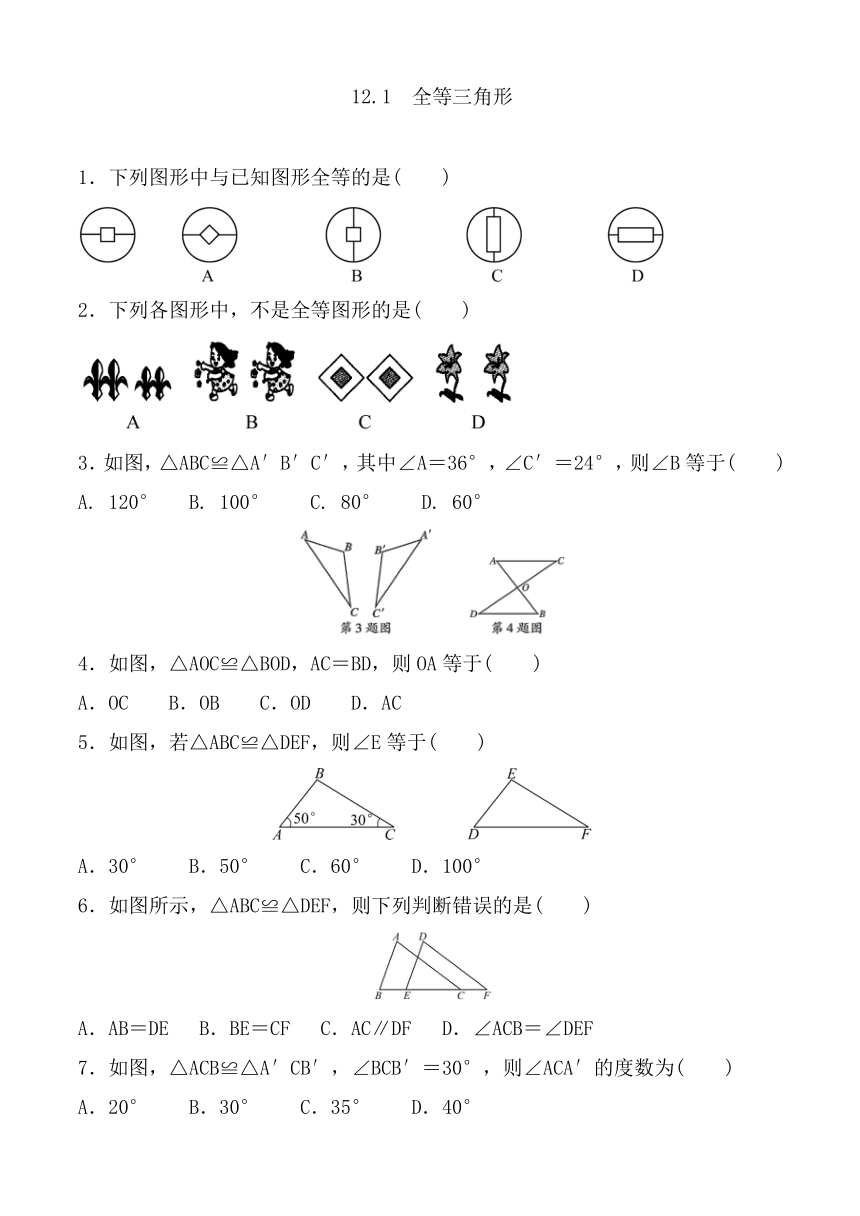
1.下列图形中与已知图形全等的是( )
2.下列各图形中,不是全等图形的是( )
3.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B等于( )
A. 120° B. 100° C. 80° D. 60°
4.如图,△AOC≌△BOD,AC=BD,则OA等于( )
A.OC B.OB C.OD D.AC
5.如图,若△ABC≌△DEF,则∠E等于( )
A.30° B.50° C.60° D.100°
6.如图所示,△ABC≌△DEF,则下列判断错误的是( )
A.AB=DE B.BE=CF C.AC∥DF D.∠ACB=∠DEF
7.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°
8.如图所示,已知△ABC≌△BAD,点A、C的对应顶点分别为B、D,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( )
A.5cm B.7cm C.10cm D.无法确定
9.如图所示,△ABC绕点A旋转就能与△ADE完全重合,则∠BAC的对应角是 ,边BC的对应边是 .
10.已知△ABC≌△A′B′C′,△ABC的周长为32cm,AB=9cm,BC=12cm,则A′C′= .
11.如图,△ABC≌△CDA,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的是 (填序号).
12. 已知△ABC≌△A′B′C′,且△ABC的周长为20,AB=8,BC=5,则A′C′= .
13. 如图,△ABC≌△EFD,写出图中的对应边、对应角.
14. 如图所示,已知△ABD≌△ACE,AD=6cm,AC=4cm,∠ABD=50°,∠E=30°,求BE的长及∠COD的度数.
15.如图,△ACF≌△DBE,∠E=∠F.若AD=11,BC=7,求线段AB的长.
16.如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.
(1)你能说明BD、DE、CE之间的数量关系吗?
(2)△ABD满足什么条件时,BD∥CE?
答案:
1-8 BAABD DBC
9. ∠DAE DE
10. 11cm
11. ②④
12. 7
13. 解: 对应边:AB与EF、AC与ED、BC与FD;对应角:∠A与∠E、∠B与∠F、∠ACB与∠EDF.
14. 解: 因为△ABD≌△ACE,所以AD=AE=6(cm),AC=AB=4(cm),所以BE=AE-AB=AD-AC=6-4=2(cm).在△OBE中,∠E=30°,且∠ABD=∠E+∠BOE=50°,所以∠BOE=20°,所以∠COD=∠BOE=20°.
15. 解:∵△ACF≌△DBE,∴AC=DB,∴AC-BC=DB-BC,即AB=CD.∵AD=11,BC=7,∴AB=(AD-BC)=×(11-7)=2,即AB=2.
16. 解:(1)BD=DE+CE.理由:∵△BAD≌△ACE,∴BD=AE,AD=CE,∴BD=AE=AD+DE=CE+DE,即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE.理由:∵△BAD≌△ACE,∴∠E=∠ADB=90°,∴∠BDE=180°-∠ADB=180°-90°=90°=∠E,∴BD∥CE.
1.下列图形中与已知图形全等的是( )
2.下列各图形中,不是全等图形的是( )
3.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B等于( )
A. 120° B. 100° C. 80° D. 60°
4.如图,△AOC≌△BOD,AC=BD,则OA等于( )
A.OC B.OB C.OD D.AC
5.如图,若△ABC≌△DEF,则∠E等于( )
A.30° B.50° C.60° D.100°
6.如图所示,△ABC≌△DEF,则下列判断错误的是( )
A.AB=DE B.BE=CF C.AC∥DF D.∠ACB=∠DEF
7.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°
8.如图所示,已知△ABC≌△BAD,点A、C的对应顶点分别为B、D,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( )
A.5cm B.7cm C.10cm D.无法确定
9.如图所示,△ABC绕点A旋转就能与△ADE完全重合,则∠BAC的对应角是 ,边BC的对应边是 .
10.已知△ABC≌△A′B′C′,△ABC的周长为32cm,AB=9cm,BC=12cm,则A′C′= .
11.如图,△ABC≌△CDA,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的是 (填序号).
12. 已知△ABC≌△A′B′C′,且△ABC的周长为20,AB=8,BC=5,则A′C′= .
13. 如图,△ABC≌△EFD,写出图中的对应边、对应角.
14. 如图所示,已知△ABD≌△ACE,AD=6cm,AC=4cm,∠ABD=50°,∠E=30°,求BE的长及∠COD的度数.
15.如图,△ACF≌△DBE,∠E=∠F.若AD=11,BC=7,求线段AB的长.
16.如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.
(1)你能说明BD、DE、CE之间的数量关系吗?
(2)△ABD满足什么条件时,BD∥CE?
答案:
1-8 BAABD DBC
9. ∠DAE DE
10. 11cm
11. ②④
12. 7
13. 解: 对应边:AB与EF、AC与ED、BC与FD;对应角:∠A与∠E、∠B与∠F、∠ACB与∠EDF.
14. 解: 因为△ABD≌△ACE,所以AD=AE=6(cm),AC=AB=4(cm),所以BE=AE-AB=AD-AC=6-4=2(cm).在△OBE中,∠E=30°,且∠ABD=∠E+∠BOE=50°,所以∠BOE=20°,所以∠COD=∠BOE=20°.
15. 解:∵△ACF≌△DBE,∴AC=DB,∴AC-BC=DB-BC,即AB=CD.∵AD=11,BC=7,∴AB=(AD-BC)=×(11-7)=2,即AB=2.
16. 解:(1)BD=DE+CE.理由:∵△BAD≌△ACE,∴BD=AE,AD=CE,∴BD=AE=AD+DE=CE+DE,即BD=DE+CE;
(2)△ABD满足∠ADB=90°时,BD∥CE.理由:∵△BAD≌△ACE,∴∠E=∠ADB=90°,∴∠BDE=180°-∠ADB=180°-90°=90°=∠E,∴BD∥CE.
