2021-2022学年人教版数学八年级上册 13.3.1 等腰三角形 同步练习 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 13.3.1 等腰三角形 同步练习 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 406.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 15:11:10 | ||
图片预览




文档简介
13.3.1 等腰三角形
一、单选题
1.有下列说法:①等腰三角形的腰相等;②等腰三角形的两底角相等,③等腰三角形的中线、高线和角平分线互相重合; ④等腰三角形两底角的平分线相等;⑤等腰三角形的腰一定大于腰上的高线其中正确的有( )个
A.1 B.2 C.3 D.4
2.如果一个三角形的外角平分线平行于三角形的一边,那么这个三角形是( )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.锐角三角形
3.如图,已知false,以点B为圆心,false长为半径画弧,交腰false于点E,则下列结论一定正确的是( )
A.false B.false C.false D.false
4.如图,false中,false,false是边false的垂直平分线,分别交false、false于点false、false,连接false,若false恰好为false的平分线,则false的度数是( )
A.false B.false C.false D.false
5.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线一点,点E在BC上,且AE=CF,∠CAE=30°,则∠ACF的度数是( )
A.75° B.60° C.55° D.45°
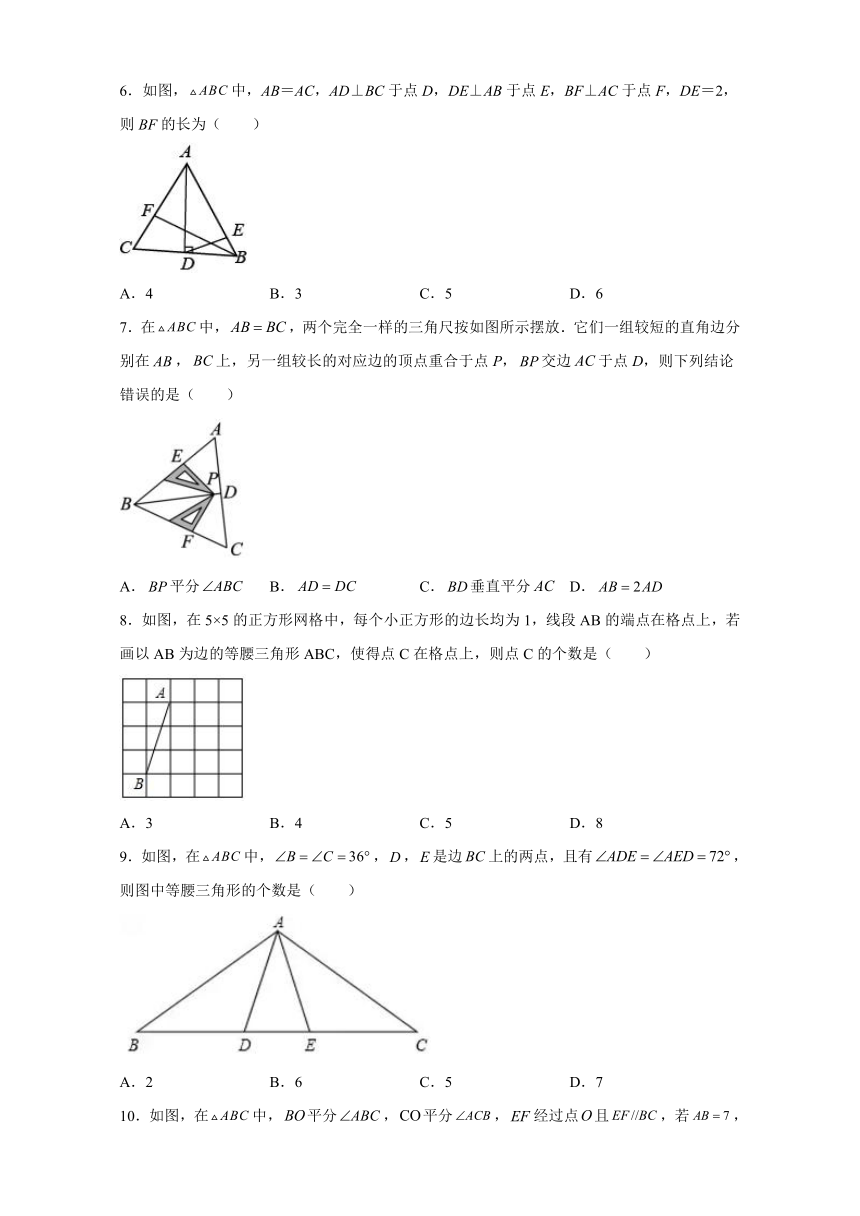
6.如图,false中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )
A.4 B.3 C.5 D.6
7.在false中,false,两个完全一样的三角尺按如图所示摆放.它们一组较短的直角边分别在false,false上,另一组较长的对应边的顶点重合于点P,false交边false于点D,则下列结论错误的是( )
A.false平分false B.false C.false垂直平分false D.false
8.如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,若画以AB为边的等腰三角形ABC,使得点C在格点上,则点C的个数是( )
A.3 B.4 C.5 D.8
9.如图,在false中,false,false,false是边false上的两点,且有false,则图中等腰三角形的个数是( )
A.2 B.6 C.5 D.7
10.如图,在false中,false平分false,false平分false,false经过点false且false,若false,false,false,则false的周长是( )
A.15 B.16 C.17 D.24
11.如图,在false中,false,false于点false,false平分false交false于点false,则下列结论一定成立的是( )
A.false B.false C.false D.false
12.如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
13.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法:①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中正确的是( )
A.①②③④ B.①②③ C.②④ D.①③
14.如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC交AC的延长线于点N,连接BD、CD.以下结论:①BM=CN;②∠DBC=∠DAN;③∠BAC+∠BDC=180°;④点D到△ABC各顶点的距离相等.正确的是( )
A.①②④ B.②③④ C.①②③ D.①③④
15.如图,在4×4的正方形网格中,记∠ABF=false,∠FCH=false,∠DGE=false,则( )
A.false<false<false B.false≤false<false C.false<false<false D.false<false<false
二、填空题
16.一个等腰三角形的底角是顶角的2倍,则顶角的大小是____.
17.如图,false中,false,将false沿false平移false得到false,false与false相交于点false,则false的长为________false.
18.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=7cm,DE=3cm,求CE的长为______cm.
19.如图,false,false,false,点D恰好落在线段AB上,则false的度数为________度.
20.如图,在△ABC中,∠ACB=90°,∠A<∠B,点D为AB边上一点且不与A、B重合,将△ACD沿CD翻折得到△ECD,直线CE与直线AB相交于点F.若∠A=40°,当△DEF为等腰三角形时,∠ACD=__________________.
三、解答题
21.一个三角形的两边b=2,c=7.
(1)当各边均为整数时,有几个三角形?
(2)若此三角形是等腰三角形,则其周长是多少?
22.如图,DE∥BC,CG=GB,∠1=∠2,求证:△DGE是等腰三角形.
23.如图,在false中,false,false,点false是边false上一点,false,作false,false交边false于点false.求证:false.
24.如图,在等腰△ABC中,BA=BC,点F在AB边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.
(1)求证:AD=CE;
(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.
25.已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,AE⊥BD于F,交BC于E.求证:
(1)AB=BE;
(2)∠CAE=false∠ABC;
(3)AD=CE;
(4)CD+CE=AB.
参考答案
1.C
解:①等腰三角形的腰相等,故正确;
②等腰三角形的两底角相等,故正确;
③等腰三角形的顶角的平分线,底边上的高,底边上的中线互相重合,故错误;
④等腰三角形两底角的平分线相等,故正确;
⑤等腰三角形的腰一定大于或等于腰上的高线,故错误;
故选:C.
2.B
解:如图,
∵DC平分∠ACE,且AB∥CD,
∴∠ACD=∠DCE,∠A=∠ACD,∠B=∠DCE,
∴∠B=∠A,
∴△ABC为等腰三角形.
故选择:B.
3.C
解:∵AB=AC,
∴∠ABC=∠ACB,
由作图可知:BE=BC,
∴∠ACB=∠BEC,
∴∠ABC=∠ACB=∠BEC,
∴∠BAC=∠EBC,
而题中无条件可证明BC=EC,AE=BE,∠EBC=∠ABE,
故选C.
4.C
解:设∠B=x°,
∵DE是边AB的垂直平分线,
∴DB=DA,
∴∠DAB=∠B=x°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=2x°,
∵BA=BC,
∴∠C=∠BAC=2x°,
在△ABC中,根据三角形的内角和定理得:x+2x+2x=180,
解得:x=36,
∴∠B=36°,
故选:C.
5.B
解:∵在△ABC中,∠ABC=90°,AB=CB,
∴∠BAC=∠BCA=45°,
∵∠CAE=30°,
∴∠BAE=15°,
在Rt△ABE和Rt△CBF中,
false ,
∴Rt△ABE≌Rt△CBF(HL)
∴∠BAE=∠BCF=15°,
∴∠ACF=∠BCA+∠BCF=60°,
故选:B.
6.A
解:过点D作DH⊥AC于点H,如图所示:
∵AB=AC,AD⊥BC,
∴AD平分∠CAB,
∵DE⊥AB,DE=2,
∴DE=DH=2,
∵false,
∴false,
∴false;
故选A.
7.D
解:如图.
由题意得,PE⊥AB,PF⊥BC,PE=PF,
∴BP平分∠ABC,
∵AB=BC,
∴AD=DC,BD垂直平分AC,
故选项A、B、C正确,不符合题意;
只有当△ABC是等边三角形时,才能得出AB=2AD,
故选项D错误,符合题意.
故选:D.
8.D
解:如图所示,
故选:D.
9.B
解:∵false,false
∴△ABC和△ADE都是等腰三角形,∠DAB=∠ADE-∠B=36°,∠EAC=∠AED-∠C=36°
∴∠DAB=∠B,∠EAC=∠C
∴△DAB和△EAC都是等腰三角形
∵∠B+∠BEA+∠BAE=180°,∠C+∠CDA+∠CAD=180°
∴∠BAE=180°-∠B-∠BEA=72°,∠CAD=180°-∠C-∠CDA=72°
∴∠BAE=∠BEA,∠CAD=∠CDA
∴△BAE和△CAD都是等腰三角形
综上:共有6个等腰三角形
故选B.
10.A
解:∵EF∥BC,
∴∠EOB=∠OBC,
∵false平分false,
∴∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴BE=OE,
同理可得:OF=CF,
∴false的周长为AE+AF+EF=AE+OE+OF+AF= AE+BE+CF+AF=AB+AC=7+8=15.
故答案为:A
11.D
解:∵false,
∴∠BAE+∠DAE+∠CAD=90°,∠B+∠C=90°
∵AD⊥BC
∴∠BAE+∠DAE+∠B=90°,∠DAE+∠DEA=90°,∠CAD+∠C=90°
∵false平分false
∴∠DAE=∠BAE
∵∠B+∠C=90°
∴∠CAD=∠B
∵∠CEA=∠B+∠BAE
∴∠CEA=∠DAE+∠CAD=∠CAE
∴AC=EC,
其他选项均缺少条件,无法证明一定相等,
故选:D.
12.B
解:∵∠ABC=∠ACB,
∴AB=AC,
∵∠BAE=∠CAD,
∴补充条件AD=AE时,△ABE≌△ACD(SAS),故选项A不符合题意;
补充条件BE=CD,无法判断△ABE≌△ACD,故选项B符合题意;
补充条件OB=OC时,则∠OBC=∠OCB,故∠ABE=∠ACD,则△ABE≌△ACD(ASA),故选项C不符合题意;
补充条件∠BDC=∠CEB时,则∠AEB=∠ADC,则△ABE≌△ACD(AAS),故选项D不符合题意;
故选:B.
13.B
解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选:B.
14.C
解:∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠BAD=∠CAD,
∵DE是BC的垂直平分线,
∴BD=DC,
在Rt△BDM和Rt△CDN中,
false,
∴Rt△BDM≌Rt△CDN(HL),
∴BM=CN,∠BDM=∠CDN,故①正确,
∴∠BDC=∠MDN,
∵∠BAC+∠AMD+∠AND+∠MDN=360°,∠AMD=∠AND=90°,
∴∠BAC+∠MDN=180°,
∴∠BAC+∠BDC=180°,故③正确,
∵BD=CD,
∴∠DBC=∠DCB,
∵∠DBC+∠DCB+∠BDC=180°,
∴∠BDC+2∠DBC=180°,
∵∠MDN+∠BAC=180°=∠MDN+2∠DAN,
∴∠DBC=∠DAN,故②正确,
在△ACD中,∠ACD>90°,
∴AD>CD,故④错误,
故选:C.
15.A
解:由图知,∠FBG<45°,
∴α=∠ABF=180°-45°-∠FBG>90°;
由图知,∠DGF=45°,∠EGH=45°,
∴γ=∠DGE=180°-∠DGF-∠EGH=180°-45°-45°=90°,
由图知,∠MCH<45°,∠BCF=45°,
∴β=∠FCH=180°-∠BCF-∠MCH=180°-45°-∠MCH<90°,
∴β<γ<α,
故选:A.
16.36°
解:180°÷(2+2+1)
=180°÷5
=36°,
顶角是36°.
故答案为:36°.
17.5
解:∵将false沿false平移false得到false,
∴BE=3cm,AB∥DE,
∴∠A=∠EGC,
∵false,
∴∠A=∠BCA,
∴∠EGC=∠BCA,
∴EG=EC=8-3=5cm,
故答案是:5.
18.4
解:∵BF、CF分别平分∠ABC、∠ACB的外角,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∴EF=DF-DE=BD-DE=7-3=4,
∴CE=4cm.
故答案为4.
19.70
解:∵false,
∴false,false,
∴false,
∵false,false,
∴false,
∴false.
故答案为:70.
20.30°或15°或60°
解:由翻折的性质可知∠E=∠A=α,∠CDE=∠ADC,
如图1,
当EF=DF时,则∠EDF=∠E=α,
∵∠EDF=∠CDE-∠CDB,∠CDB=∠A+∠ACD,
∴α=∠ADC-(∠A+∠ACD)
=180°-2(∠A+∠ACD)
=180°-2(α+∠ACD),
∴∠ACD=90°-false×40°=30°,
∴当∠ACD=30°时,△DEF为等腰三角形,
当ED=EF时,∠EDF=∠EFD=false=70°,
∴2∠ADC=180°+∠EDF=250°,
∴∠ADC=125°,
∴∠ACD=180°-∠A-∠ADC=180°-∠A-125°=15°,
∵∠DFE=∠A+∠ACF,
∴∠DFE≠∠DEF,
如图2,
当DE=EF时,∠EDF=∠EFD=false∠A=20°;
∴∠ACF=180°-∠A-∠EFD=120°,
∴∠ACD=false∠ACF=60°;
综上:当∠ACD=30°或15°或60°时,△DEF为等腰三角形,
故答案为:30°或15°或60°.
21.(1)a=6或7或8,有三个三角形;(2)周长为16.
解:(1)设第三边长为a,则5<a< 9
由于三角形的各边均为整数,则a=6或7或8,因此有三个三角形;
(2)当a=7时,有a=7= c,由2+7>7,所以周长为7+7+2=16;
当a=2时,有a=2= c,由2+2<7,故不能构成三角形,综上其周长只能为16
22.见详解
解:连接AG,
∵DE∥BC,
∴∠ABC=∠1,∠ACB=∠2.
又∵∠1=∠2,
∴∠ABC=∠ACB.
∴AB=AC,
又∵G为BC中点,
∴AG⊥BC.
∴AG⊥DE
∵∠1=∠2,
∴AD=AE,
∴AG垂直平分DE,
∴DG=GE.
∴△DGE是等腰三角形.
23.证明见解析
证明:∵false,false,
∴false,
∵false,
∴false,
∴false,
∵false,false,
∴false,
在false和false中,
false,
∴false≌false,
∴false.
24.(1)证明见解析;(2)false
解:(1)∵∠ABC=∠DBE,
∴false,
即false,
在false和false中,
false,
∴false≌false,
∴AD=CE;
(2)∵∠ABC=30°,∠AFC=45°,
∴false,
∵false≌false,
∴false
∵BA=BC,
∴false,
∴false.
25.(1)见详解;(2)见详解;(3)见详解;(4)见详解
证明:(1)∵BD平分∠ABC,AE⊥BD,
∴∠ABF=∠EBF,∠AFB=∠EFB=90°,
在△ABF和△EBF中,
false ,
∴△ABF≌△EBF(ASA),
∴AB=BE;
(2)∵∠BAC=90°,
∴∠CAE+∠BAF=90°,而∠BAF+∠ABF=90°,
∴∠CAE=∠ABF=false ∠ABC;
(3)连接DE,
在△ABD和△EBD中
∵false,
∴△ABD≌△EBD(SAS),
∴AD=DE,∠DEC=∠BAC=90°,
∵∠BAC=90°,AB=AC,
∴∠C=45°,
∴CE=DE,
∴AD=CE;
(4)由(3)可得AD=CE,
∴CD+CE =CD+AD=AC=AB.
一、单选题
1.有下列说法:①等腰三角形的腰相等;②等腰三角形的两底角相等,③等腰三角形的中线、高线和角平分线互相重合; ④等腰三角形两底角的平分线相等;⑤等腰三角形的腰一定大于腰上的高线其中正确的有( )个
A.1 B.2 C.3 D.4
2.如果一个三角形的外角平分线平行于三角形的一边,那么这个三角形是( )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.锐角三角形
3.如图,已知false,以点B为圆心,false长为半径画弧,交腰false于点E,则下列结论一定正确的是( )
A.false B.false C.false D.false
4.如图,false中,false,false是边false的垂直平分线,分别交false、false于点false、false,连接false,若false恰好为false的平分线,则false的度数是( )
A.false B.false C.false D.false
5.如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线一点,点E在BC上,且AE=CF,∠CAE=30°,则∠ACF的度数是( )
A.75° B.60° C.55° D.45°
6.如图,false中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )
A.4 B.3 C.5 D.6
7.在false中,false,两个完全一样的三角尺按如图所示摆放.它们一组较短的直角边分别在false,false上,另一组较长的对应边的顶点重合于点P,false交边false于点D,则下列结论错误的是( )
A.false平分false B.false C.false垂直平分false D.false
8.如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,若画以AB为边的等腰三角形ABC,使得点C在格点上,则点C的个数是( )
A.3 B.4 C.5 D.8
9.如图,在false中,false,false,false是边false上的两点,且有false,则图中等腰三角形的个数是( )
A.2 B.6 C.5 D.7
10.如图,在false中,false平分false,false平分false,false经过点false且false,若false,false,false,则false的周长是( )
A.15 B.16 C.17 D.24
11.如图,在false中,false,false于点false,false平分false交false于点false,则下列结论一定成立的是( )
A.false B.false C.false D.false
12.如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
13.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法:①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中正确的是( )
A.①②③④ B.①②③ C.②④ D.①③
14.如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC交AC的延长线于点N,连接BD、CD.以下结论:①BM=CN;②∠DBC=∠DAN;③∠BAC+∠BDC=180°;④点D到△ABC各顶点的距离相等.正确的是( )
A.①②④ B.②③④ C.①②③ D.①③④
15.如图,在4×4的正方形网格中,记∠ABF=false,∠FCH=false,∠DGE=false,则( )
A.false<false<false B.false≤false<false C.false<false<false D.false<false<false
二、填空题
16.一个等腰三角形的底角是顶角的2倍,则顶角的大小是____.
17.如图,false中,false,将false沿false平移false得到false,false与false相交于点false,则false的长为________false.
18.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=7cm,DE=3cm,求CE的长为______cm.
19.如图,false,false,false,点D恰好落在线段AB上,则false的度数为________度.
20.如图,在△ABC中,∠ACB=90°,∠A<∠B,点D为AB边上一点且不与A、B重合,将△ACD沿CD翻折得到△ECD,直线CE与直线AB相交于点F.若∠A=40°,当△DEF为等腰三角形时,∠ACD=__________________.
三、解答题
21.一个三角形的两边b=2,c=7.
(1)当各边均为整数时,有几个三角形?
(2)若此三角形是等腰三角形,则其周长是多少?
22.如图,DE∥BC,CG=GB,∠1=∠2,求证:△DGE是等腰三角形.
23.如图,在false中,false,false,点false是边false上一点,false,作false,false交边false于点false.求证:false.
24.如图,在等腰△ABC中,BA=BC,点F在AB边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.
(1)求证:AD=CE;
(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.
25.已知:如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC,交AC于D,AE⊥BD于F,交BC于E.求证:
(1)AB=BE;
(2)∠CAE=false∠ABC;
(3)AD=CE;
(4)CD+CE=AB.
参考答案
1.C
解:①等腰三角形的腰相等,故正确;
②等腰三角形的两底角相等,故正确;
③等腰三角形的顶角的平分线,底边上的高,底边上的中线互相重合,故错误;
④等腰三角形两底角的平分线相等,故正确;
⑤等腰三角形的腰一定大于或等于腰上的高线,故错误;
故选:C.
2.B
解:如图,
∵DC平分∠ACE,且AB∥CD,
∴∠ACD=∠DCE,∠A=∠ACD,∠B=∠DCE,
∴∠B=∠A,
∴△ABC为等腰三角形.
故选择:B.
3.C
解:∵AB=AC,
∴∠ABC=∠ACB,
由作图可知:BE=BC,
∴∠ACB=∠BEC,
∴∠ABC=∠ACB=∠BEC,
∴∠BAC=∠EBC,
而题中无条件可证明BC=EC,AE=BE,∠EBC=∠ABE,
故选C.
4.C
解:设∠B=x°,
∵DE是边AB的垂直平分线,
∴DB=DA,
∴∠DAB=∠B=x°,
∵AD平分∠BAC,
∴∠BAC=2∠BAD=2x°,
∵BA=BC,
∴∠C=∠BAC=2x°,
在△ABC中,根据三角形的内角和定理得:x+2x+2x=180,
解得:x=36,
∴∠B=36°,
故选:C.
5.B
解:∵在△ABC中,∠ABC=90°,AB=CB,
∴∠BAC=∠BCA=45°,
∵∠CAE=30°,
∴∠BAE=15°,
在Rt△ABE和Rt△CBF中,
false ,
∴Rt△ABE≌Rt△CBF(HL)
∴∠BAE=∠BCF=15°,
∴∠ACF=∠BCA+∠BCF=60°,
故选:B.
6.A
解:过点D作DH⊥AC于点H,如图所示:
∵AB=AC,AD⊥BC,
∴AD平分∠CAB,
∵DE⊥AB,DE=2,
∴DE=DH=2,
∵false,
∴false,
∴false;
故选A.
7.D
解:如图.
由题意得,PE⊥AB,PF⊥BC,PE=PF,
∴BP平分∠ABC,
∵AB=BC,
∴AD=DC,BD垂直平分AC,
故选项A、B、C正确,不符合题意;
只有当△ABC是等边三角形时,才能得出AB=2AD,
故选项D错误,符合题意.
故选:D.
8.D
解:如图所示,
故选:D.
9.B
解:∵false,false
∴△ABC和△ADE都是等腰三角形,∠DAB=∠ADE-∠B=36°,∠EAC=∠AED-∠C=36°
∴∠DAB=∠B,∠EAC=∠C
∴△DAB和△EAC都是等腰三角形
∵∠B+∠BEA+∠BAE=180°,∠C+∠CDA+∠CAD=180°
∴∠BAE=180°-∠B-∠BEA=72°,∠CAD=180°-∠C-∠CDA=72°
∴∠BAE=∠BEA,∠CAD=∠CDA
∴△BAE和△CAD都是等腰三角形
综上:共有6个等腰三角形
故选B.
10.A
解:∵EF∥BC,
∴∠EOB=∠OBC,
∵false平分false,
∴∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴BE=OE,
同理可得:OF=CF,
∴false的周长为AE+AF+EF=AE+OE+OF+AF= AE+BE+CF+AF=AB+AC=7+8=15.
故答案为:A
11.D
解:∵false,
∴∠BAE+∠DAE+∠CAD=90°,∠B+∠C=90°
∵AD⊥BC
∴∠BAE+∠DAE+∠B=90°,∠DAE+∠DEA=90°,∠CAD+∠C=90°
∵false平分false
∴∠DAE=∠BAE
∵∠B+∠C=90°
∴∠CAD=∠B
∵∠CEA=∠B+∠BAE
∴∠CEA=∠DAE+∠CAD=∠CAE
∴AC=EC,
其他选项均缺少条件,无法证明一定相等,
故选:D.
12.B
解:∵∠ABC=∠ACB,
∴AB=AC,
∵∠BAE=∠CAD,
∴补充条件AD=AE时,△ABE≌△ACD(SAS),故选项A不符合题意;
补充条件BE=CD,无法判断△ABE≌△ACD,故选项B符合题意;
补充条件OB=OC时,则∠OBC=∠OCB,故∠ABE=∠ACD,则△ABE≌△ACD(ASA),故选项C不符合题意;
补充条件∠BDC=∠CEB时,则∠AEB=∠ADC,则△ABE≌△ACD(AAS),故选项D不符合题意;
故选:B.
13.B
解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故选:B.
14.C
解:∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠BAD=∠CAD,
∵DE是BC的垂直平分线,
∴BD=DC,
在Rt△BDM和Rt△CDN中,
false,
∴Rt△BDM≌Rt△CDN(HL),
∴BM=CN,∠BDM=∠CDN,故①正确,
∴∠BDC=∠MDN,
∵∠BAC+∠AMD+∠AND+∠MDN=360°,∠AMD=∠AND=90°,
∴∠BAC+∠MDN=180°,
∴∠BAC+∠BDC=180°,故③正确,
∵BD=CD,
∴∠DBC=∠DCB,
∵∠DBC+∠DCB+∠BDC=180°,
∴∠BDC+2∠DBC=180°,
∵∠MDN+∠BAC=180°=∠MDN+2∠DAN,
∴∠DBC=∠DAN,故②正确,
在△ACD中,∠ACD>90°,
∴AD>CD,故④错误,
故选:C.
15.A
解:由图知,∠FBG<45°,
∴α=∠ABF=180°-45°-∠FBG>90°;
由图知,∠DGF=45°,∠EGH=45°,
∴γ=∠DGE=180°-∠DGF-∠EGH=180°-45°-45°=90°,
由图知,∠MCH<45°,∠BCF=45°,
∴β=∠FCH=180°-∠BCF-∠MCH=180°-45°-∠MCH<90°,
∴β<γ<α,
故选:A.
16.36°
解:180°÷(2+2+1)
=180°÷5
=36°,
顶角是36°.
故答案为:36°.
17.5
解:∵将false沿false平移false得到false,
∴BE=3cm,AB∥DE,
∴∠A=∠EGC,
∵false,
∴∠A=∠BCA,
∴∠EGC=∠BCA,
∴EG=EC=8-3=5cm,
故答案是:5.
18.4
解:∵BF、CF分别平分∠ABC、∠ACB的外角,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∴EF=DF-DE=BD-DE=7-3=4,
∴CE=4cm.
故答案为4.
19.70
解:∵false,
∴false,false,
∴false,
∵false,false,
∴false,
∴false.
故答案为:70.
20.30°或15°或60°
解:由翻折的性质可知∠E=∠A=α,∠CDE=∠ADC,
如图1,
当EF=DF时,则∠EDF=∠E=α,
∵∠EDF=∠CDE-∠CDB,∠CDB=∠A+∠ACD,
∴α=∠ADC-(∠A+∠ACD)
=180°-2(∠A+∠ACD)
=180°-2(α+∠ACD),
∴∠ACD=90°-false×40°=30°,
∴当∠ACD=30°时,△DEF为等腰三角形,
当ED=EF时,∠EDF=∠EFD=false=70°,
∴2∠ADC=180°+∠EDF=250°,
∴∠ADC=125°,
∴∠ACD=180°-∠A-∠ADC=180°-∠A-125°=15°,
∵∠DFE=∠A+∠ACF,
∴∠DFE≠∠DEF,
如图2,
当DE=EF时,∠EDF=∠EFD=false∠A=20°;
∴∠ACF=180°-∠A-∠EFD=120°,
∴∠ACD=false∠ACF=60°;
综上:当∠ACD=30°或15°或60°时,△DEF为等腰三角形,
故答案为:30°或15°或60°.
21.(1)a=6或7或8,有三个三角形;(2)周长为16.
解:(1)设第三边长为a,则5<a< 9
由于三角形的各边均为整数,则a=6或7或8,因此有三个三角形;
(2)当a=7时,有a=7= c,由2+7>7,所以周长为7+7+2=16;
当a=2时,有a=2= c,由2+2<7,故不能构成三角形,综上其周长只能为16
22.见详解
解:连接AG,
∵DE∥BC,
∴∠ABC=∠1,∠ACB=∠2.
又∵∠1=∠2,
∴∠ABC=∠ACB.
∴AB=AC,
又∵G为BC中点,
∴AG⊥BC.
∴AG⊥DE
∵∠1=∠2,
∴AD=AE,
∴AG垂直平分DE,
∴DG=GE.
∴△DGE是等腰三角形.
23.证明见解析
证明:∵false,false,
∴false,
∵false,
∴false,
∴false,
∵false,false,
∴false,
在false和false中,
false,
∴false≌false,
∴false.
24.(1)证明见解析;(2)false
解:(1)∵∠ABC=∠DBE,
∴false,
即false,
在false和false中,
false,
∴false≌false,
∴AD=CE;
(2)∵∠ABC=30°,∠AFC=45°,
∴false,
∵false≌false,
∴false
∵BA=BC,
∴false,
∴false.
25.(1)见详解;(2)见详解;(3)见详解;(4)见详解
证明:(1)∵BD平分∠ABC,AE⊥BD,
∴∠ABF=∠EBF,∠AFB=∠EFB=90°,
在△ABF和△EBF中,
false ,
∴△ABF≌△EBF(ASA),
∴AB=BE;
(2)∵∠BAC=90°,
∴∠CAE+∠BAF=90°,而∠BAF+∠ABF=90°,
∴∠CAE=∠ABF=false ∠ABC;
(3)连接DE,
在△ABD和△EBD中
∵false,
∴△ABD≌△EBD(SAS),
∴AD=DE,∠DEC=∠BAC=90°,
∵∠BAC=90°,AB=AC,
∴∠C=45°,
∴CE=DE,
∴AD=CE;
(4)由(3)可得AD=CE,
∴CD+CE =CD+AD=AC=AB.
