一元二次方程

(共41张PPT)
实际问题
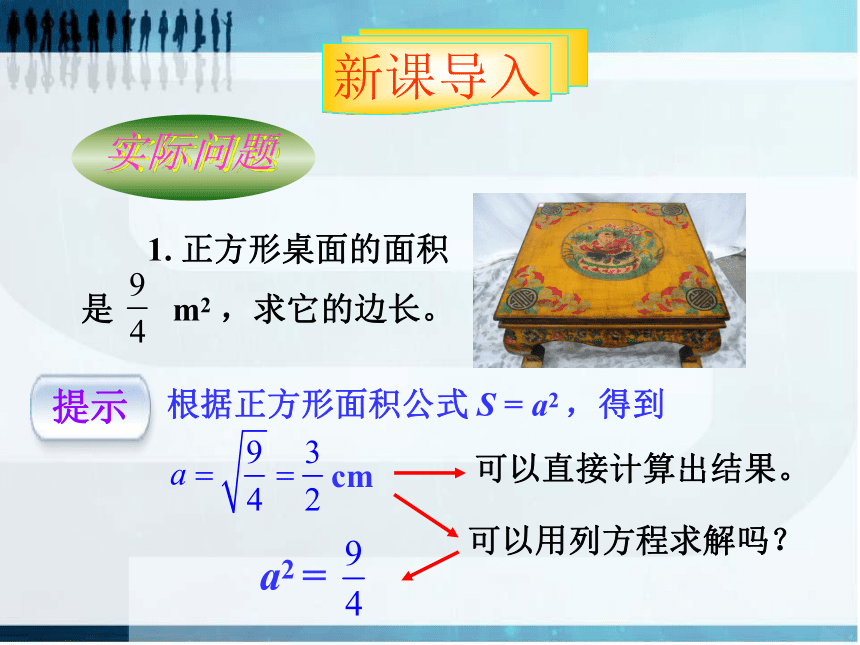
1. 正方形桌面的面积是 m2 ，求它的边长。
可以直接计算出结果。
提示
根据正方形面积公式 S = a2 ，得到
cm
可以用列方程求解吗？
a2 =
新课导入
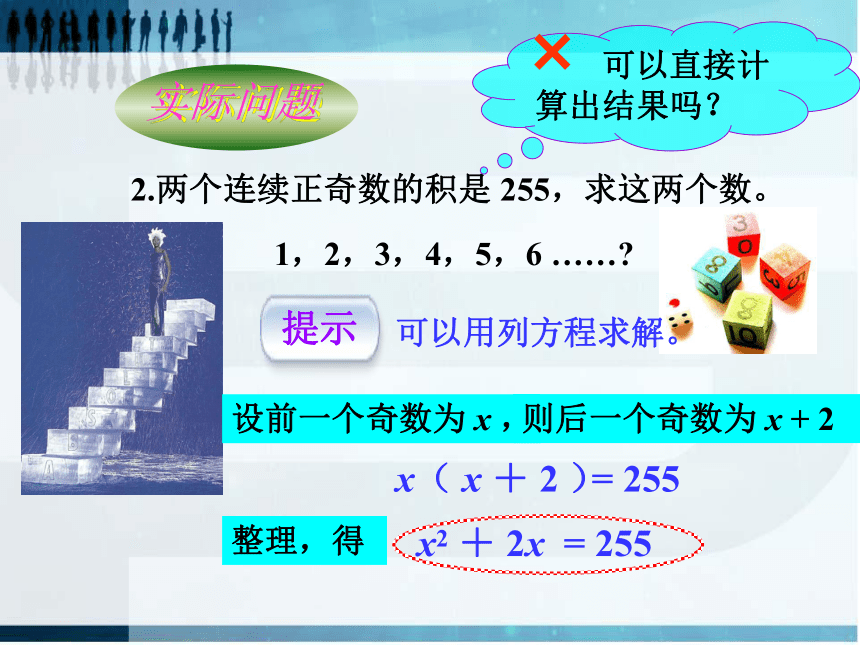
2.两个连续正奇数的积是 255，求这两个数。
实际问题
可以直接计算出结果吗？
1，2，3，4，5，6 ……
可以用列方程求解。
提示
设前一个奇数为 x ，
则后一个奇数为 x + 2
×
x（ x ＋ 2 ）
= 255
整理，得
x2 ＋ 2x = 255
【知识与能力】
了解一元二次方程的概念、一般式 ax2 ＋ bx ＋ c = 0（a≠0）及其派生的概念。
应用一元二次方程概念解决一些简单题目。通过设置问题，建立数学模型，模仿一元一次方程概念给一元二次方程下定义。　　
教学目标
【过程与方法】
通过丰富的实例，让学生合作探讨，老师点评分析，建立数学模型。根据数学模型恰如其分地给出一元二次方程的概念。
结合八册上整式中的有关概念介绍一元二次方程的派生概念，如二次项等。
【情感态度与价值观】
经历由事实问题中抽象出一元二次方程等有关概念的过程，使同学们体会到通过一元二次方程也是刻画现实世界中的数量关系的一个有效数学模型。
一元二次方程概念、一般形式及有关概念。
判定一个数是否是方程的根。
由实际问题列出的一元二次方程，解出根后还要考虑这些根是否确定是实际问题的根。
教学重难点
x2 ＋ 2x = 255
像这样的方程有广泛的应用，继续解决一些实际问题，总结一元二次方程的概念。
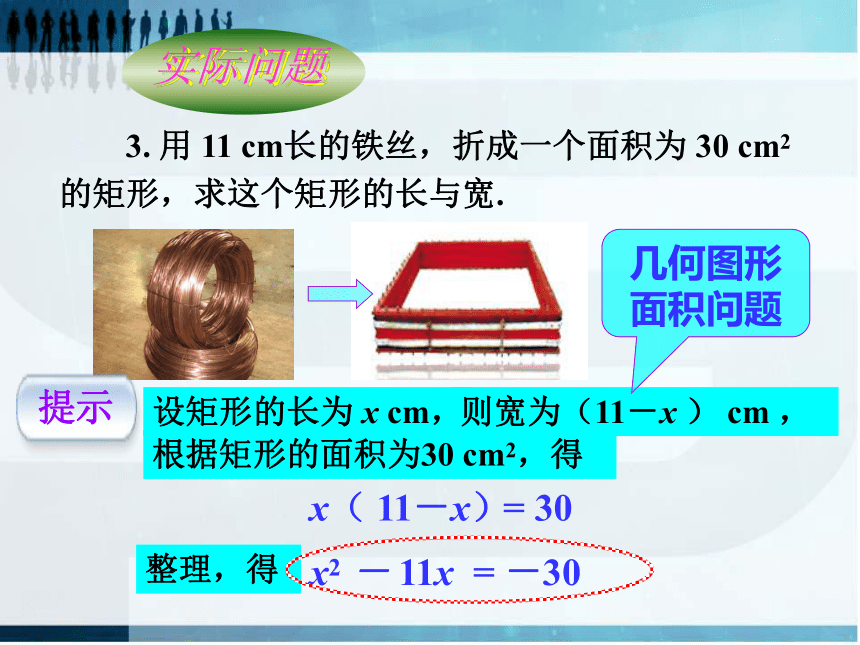
3. 用 11 cm长的铁丝，折成一个面积为 30 cm2的矩形，求这个矩形的长与宽.
实际问题
设矩形的长为 x cm，
则宽为（11－x ） cm ，
x（ 11－x）
整理，得
x2 － 11x = －30
提示
根据矩形的面积为30 cm2，得
= 30
几何图形面积问题
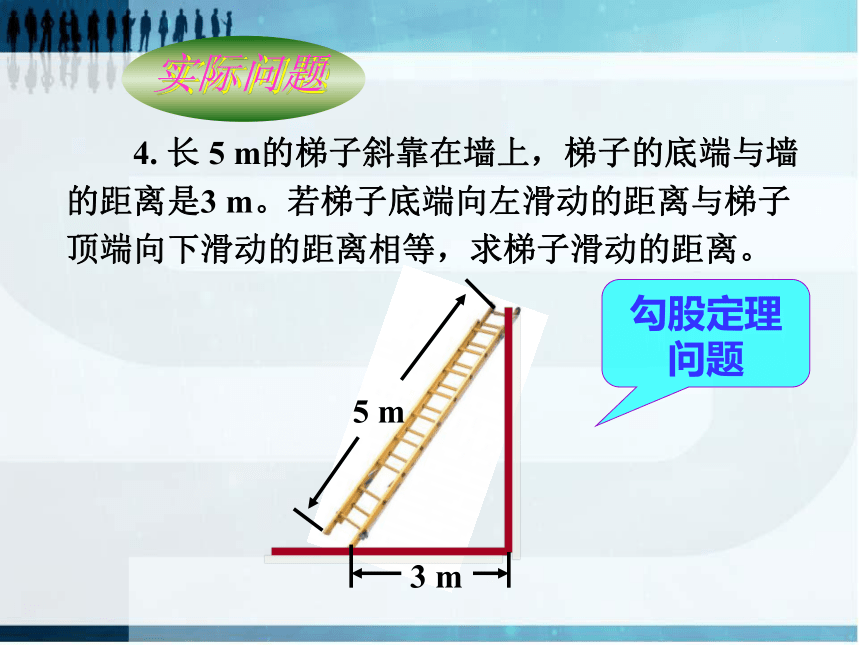
4. 长 5 m的梯子斜靠在墙上，梯子的底端与墙的距离是3 m。若梯子底端向左滑动的距离与梯子顶端向下滑动的距离相等，求梯子滑动的距离。
实际问题
5 m
3 m
勾股定理问题
3 m
5 m
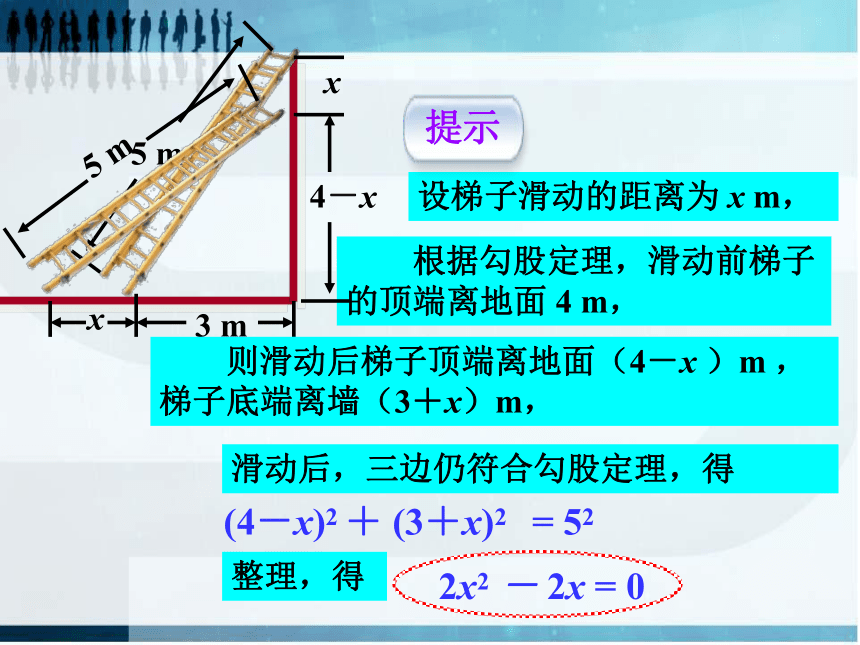
设梯子滑动的距离为 x m，
则滑动后梯子顶端离地面（4－x ）m ，梯子底端离墙（3＋x）m，
根据勾股定理，滑动前梯子的顶端离地面 4 m，
提示
(4－x)2 ＋ (3＋x)2
滑动后，三边仍符合勾股定理，得
= 52
5 m
x
4－x
x
整理，得
2x2 － 2x = 0
实际问题
5. 你遇到过下面的难题吗？你知道竹竿有多长吗？请看动画。
整理，得
设竹竿的长为 x 尺，
根据勾股定理，得
(x－3)2 ＋ (x－6)2
= x2
x2－18x＋45 = 0
提示
勾股定理问题
3尺
6尺
x－ 3
x－ 6
观 察
x2 ＋ 2x = 255
a2 =
x2 － 11x = － 30
2x2 － 2x = 0
x2－18x＋45 = 0
这些方程有什么共同点？
方程两边都是整式。
方程中只含有一个未知数。
未知数的最高次数是2。
知识要点
一元
方程两边都是整式，只含有一个未知数，并且未知数的最高次数是2的方程，叫做一元二次方程（quadratic equation in one unknown）。
二次
抢答
下列哪些是一元二次方程？
√
×
√
×
×
√
判断一个方程是否为一元二次方程，不能只看表面，能化简时应先化简。
一元二次方程必须符合三个条件
整式方程。
一个未知数。
未知数的最高次数为 2。
x2 ＋ 2x = 255
a2 =
x2 － 11x = － 30
2x2 － 2x = 0
x2－18x＋45 = 0
……
一元二次方程有很多很多，你能表示出它们的一般形式吗？
ax2 + bx +c = 0
二次项
一次项
常数项
二次项系数
一次项系数
a≠0
一元二次方程的一般形式
知识要点
当 a = 0 时，方程变为 bx＋c = 0 ，不再是一元二次方程。
为什么要限制a≠0，b、c 可以为零吗？
的强调
ax2 + bx +c = 0
“ = ”左边最多有三项，一次项、常数项可不出现，但二次项必须有。
“ = ”左边按未知数 x 的降幂排列。
“ = ”右边必须整理为 0。
例题
将方程 化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数及常数项。
其中二次项系数为 4，
解：
去括号，得：
移项，合并同类项，得一般形式为：
一次项系数为 －26，
常数项为 22。
例题
将方程 化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数及常数项。
其中二次项系数为 2，
解：
去括号，得：
移项，合并同类项，得一般形式为：
一次项系数为 2，
常数项为－4。
x
两个连续正奇数的积是 255，求这两个数。
设前一个奇数为 x ，
则后一个奇数为 x + 2，
x（ x ＋ 2 ）
= 255
整理，得
x2 ＋ 2x = 255
前面的“实际问题2”中：
回顾
1
3
…
…
…
…
11
143
13
195
15
255
－1
1
－17
255
－15
195
0
0
前面的“实际问题 4”中：
回顾
x
0
0
1
0
2
4
…
…
3
12
4
24
5
40
6
60
7
84
5 m
3 m
设梯子滑动的距离为 x m，
2x2 － 2x = 0
长 5 m的梯子斜靠在墙上，梯子的底端与墙的距离是3 m。若梯子底端向左滑动的距离与梯子顶端向下滑动的距离相等，求梯子滑动的距离。
x =－17
归纳
当
时，
x = 15
当
时，
x2 ＋ 2x = 255
x = 0
当
时，
x = 1
当
时，
2x2 － 2x = 0
x =－17，x = 15 都是方程 x2 ＋ 2x = 255 的解。
x = 0，x = 1 都是方程 2x2 － 2x =0 的解。
为了与以前所学的一元一次方程等只有一个解的区别，我们称： 一元二次方程的解也叫做一元二次方程的根（root）。
知识要点
x =－17，x = 15 都是方程 x2 ＋ 2x = 255 的解。
x = 0，x = 1 都是方程 2x2 － 2x =0 的解。
两个连续正奇数的积是 255，求这两个数。
x =－17，x = 15 都是方程 x2 ＋ 2x = 255 的解。
这两个解都是该实际问题的答案吗？
观 察
只有 x = 15 是该题的答案。
即这两个正奇数为 15、17。
注意
由实际问题列出方程并得出方程的解后，还要考虑这些解是否确实是实际问题的解。
抢答
下列方程的根是什么？
只含有一个未知数，并且未知数的最高次数是 2的整式方程叫做一元二次方程。
1.一元二次方程的概念：
2.一元二次方程的一般形式:
一般地，任何一个关于 x 的一元二次方程都可以化为 （a，b，c为常数，a≠0）的形式，称为一元二次方程的一般形式。
课堂小结
也叫做一元二次方程的根。
3. 一元二次方程的解：
4. 实际问题与一元二次方程的联系：
将实际问题转化为一元二次方程并得出解后，要考虑是否符合题目要求及实际情况。
1. 求证：关于 x 的方程（m2－8m+17）x2 + 2mx + 1 = 0， 不论 m 取何值，该方程都是一元二次方程。
证明：
即二次项系数不等于 0，不论 m 取何值，该方程都是一元二次方程。
随堂练习
2. 根据下列问题，列出关于 的方程，并将其化为一元二次方程的一般形式：
（1）4个完全相同的正方形的面积之和是25，求正方形的边长 ；
（2）一个矩形的长比宽多2，面积是100，求矩形的长 ；
（3）把长为1的木条分成两段，使较短一段的长与全长的积，等于较长一段的长的平方，求较短一段的长 ；
（4）一个直角三角形的斜边长为10，两条直角边相差2，求较长的直角边长 ；
3. 将下列方程化为一元二次方程的一般形式，并写出其中的二次项系数、一次项系数及常数项。
原
方
程 一
般
形
式 二次项系数 一次项系数 常数项
5
－1
－4
4
－81
0
4
－25
8
3
1
－7
4. 下面哪些数是方程 的根？
－4，－3，－2，－1，0，1，2，3，4．
解：将上面的这些数代入后，
只有－2和－3满足方程的等式，
所以 x =－2或 x =－3是一元二次方程的两根。
5. 试写出方程 的根，你能写出几个？
根分别为0，1。
习题答案
（1）3x2－6x＋1= 0，3，-6，1
（2）4x2＋5x－81= 0，4，5，－81
（3）x2＋5x = 0，1，5，0
（4）x2－2x＋1= 0，1，－2，1
（5）x2＋10 = 0，1，0，10
（6）x2＋2x－2= 0，1，2，－2