第10讲 角的认识和分类 讲义(含答案)
文档属性
| 名称 | 第10讲 角的认识和分类 讲义(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览




文档简介
教师讲义
年 级: 辅导科目: 数学 课时数:
课 题
角的分类
教学目的
1.余角、补角及对顶角的定义
2.余角、补角及对顶角的性质
教学内容
一、日校回顾
二、上节课知识点回顾
检查上次所留作业
三、知识梳理
1定义:
互为余角的 个角满足的条件:
互为补角的 个角满足的条件:
互为对顶角的 个角满足的条件:
2性质:
的余角相等
的补角相等
对顶角
四、例题讲解
余角的定义和性质
(1)若∠A+∠B=90°,∠B+∠C=90°,则∠A______∠C,理由是_________________;
(2)∠α=50°24′,那么∠α的余角等于____________。毛
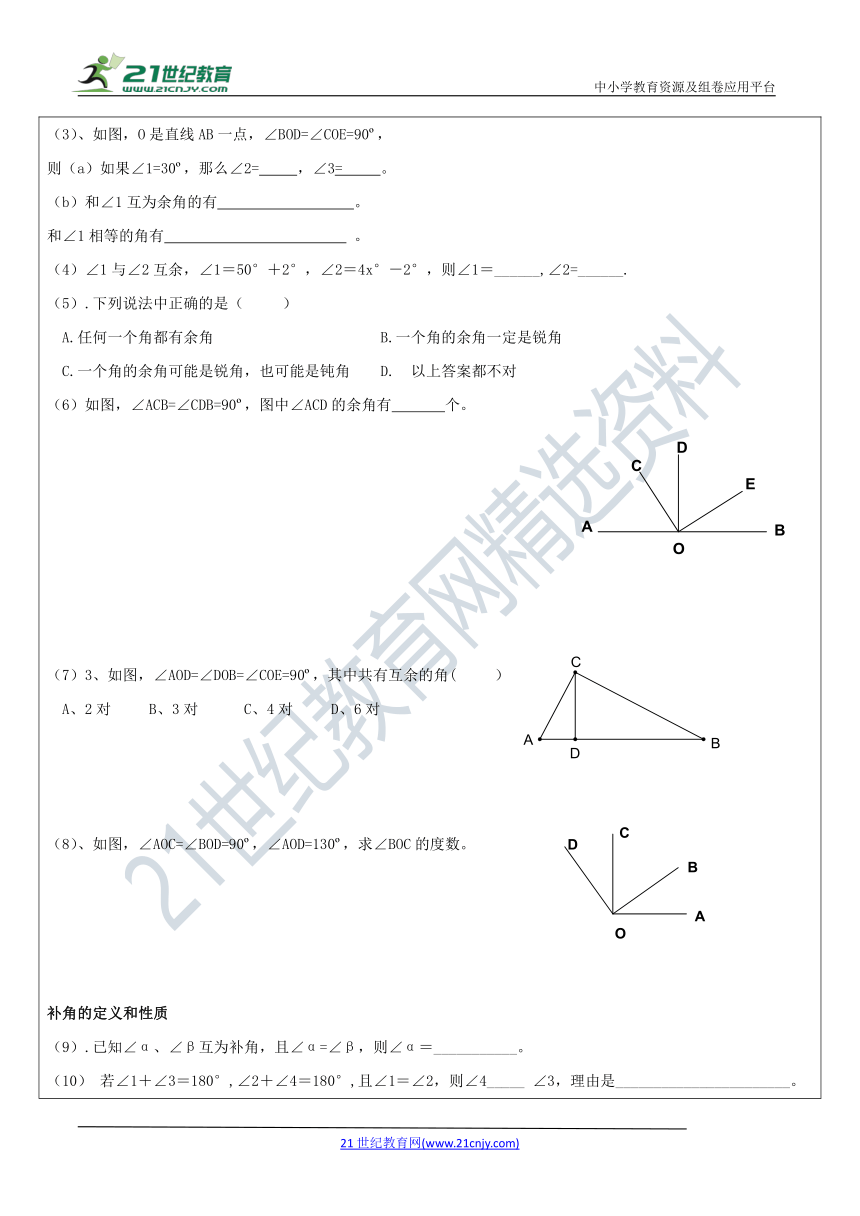
(3)、如图,O是直线AB一点,∠BOD=∠COE=90?,
则(a)如果∠1=30?,那么∠2= ,∠3= 。
(b)和∠1互为余角的有 。
和∠1相等的角有 。
(4)∠1与∠2互余,∠1=50°+2°,∠2=4x°-2°,则∠1=______,∠2=______.
(5).下列说法中正确的是( )
A.任何一个角都有余角 B.一个角的余角一定是锐角
C.一个角的余角可能是锐角,也可能是钝角 D. 以上答案都不对
(6)如图,∠ACB=∠CDB=90?,图中∠ACD的余角有 个。
(7)3、如图,∠AOD=∠DOB=∠COE=90?,其中共有互余的角( )
A、2对 B、3对 C、4对 D、6对
(8)、如图,∠AOC=∠BOD=90?,∠AOD=130?,求∠BOC的度数。
补角的定义和性质
(9).已知∠α、∠β互为补角,且∠α=∠β,则∠α=___________。
(10) 若∠1+∠3=180°,∠2+∠4=180°,且∠1=∠2,则∠4_____ ∠3,理由是_______________________。
(11) 下列说法正确的是( )
A.一个角的补角一定大于这个角; B.任何一个角都有补角
C.若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余
D.一个角如有余角,则这个角的补角与它的余角的差为90°
(12)若互补的两个角有一条公共边,则这两个角的平分线所形成的角( )
A.一定是直角 B.一定是锐角 C.一定是钝角 D.是直角或者是锐角
(13)、若∠1与∠2互为补角,且∠1<∠2,则∠1的余角是 ( )
A、∠1 B、∠1+∠2 C、(∠1+∠2) D、(∠2-∠1)
(14)、如图,O是直线BD上一点,∠BOC=36?,∠AOB=108?,
则与∠AOB互补的角有 。
(15)已知一个角的余角比它的补角的4/9还少6?,求这个角
(16)如图,O是直线AB上的一点,OM是∠AOC的角平分线,ON是∠BOC的角平分线,
(1)图中互余的角有几对?
(2)图中互补的角有几对?
对顶角的定义及性质
(17) 下列说法中正确的是( )
A.有公共顶点的角是对顶角 B.相等的角是对顶角
C.对顶角必相等 D.不是对顶角的角不相等
(18)三条线相交于一点,所成的小于平角的对顶角有( )
A.3对 B.4 对 C.5对 D.6对
(19)已知如图,三条直线AB、CD、EF交于一点,若∠1=30°,∠2=70°,求∠3的度数。
例题讲解答案:
(1)=, 同角的余角相等
(2) 39°36′
(3)(a) 60?,30?(b)∠2∠4,∠3;
(4)52°,38°
(5)B
(6)2
(7)C
(8)50 ?
(9)90°
(10)=,等角的补角相等
(11)D
(12)D
(13)D
(14)∠ AOD,∠AOC
(15)28.8?
(16) 4 、 5
(17)C
(18)D
(19)∵直线AB、CD、DF交于一点
∴2∠1+2∠2+2∠3=360°
∴∠1+∠2+∠3=180°
又∵∠1=30,∠2=70°
∴∠3=180°-∠1-∠2=80°
五、课堂练习
(1)∠1与∠2互余,∠1=(6x+8)?,∠2=(4x-8)?,则∠1= ,∠2=
(2)已知互余两个角的差是30?,则这两个角的度数分别是________________。
(3)16.如图4,ACB是直线,AB⊥CD,EC⊥FC,图中共有( )对角互余
A.2 B.3 C.4 D.以上都不对
(4)一个锐角的补角比这个角的余角大 ( )
A、30? B、45? C、60? D、90?
(5)一个角的补角是 ( )
A、锐角 B、直角 C、钝角 D、以上三种情况都有可能
(6)、若∠1与∠2互补,∠3与∠1互余,∠2+∠3=240?,由∠2是∠1的 ( )
A、2倍 B、5倍 C、11倍 D、无法确定倍数
(7)若∠1和∠2互余,∠2 和∠3 互补,∠1=63°,则∠3 =________.
(8)如图1,直线AB和CD相交于点O,∠DOE是直角,若∠1=30°,则∠2=________,∠3=________。∠4=__________。
(9)如图2,直线a、b、c两两相交,∠1=60°,∠2=false∠4,则∠3=_____,∠5=_______。
(10) 若一个角的补角是这个角的余角的3倍,则这个角是( )
A.30° B.45° C.60° D.75°
(11).如图,∠1>∠2,那么∠2与false(∠1-∠2)之间的关系是( )
A.互余 B.互补 C.和为45° D.22.5°
课堂练习答案
(1) 58? ,32?,
(2)60?,30?
(3)C
(4)D
(5)D
(6)C
(7)153°
(8)60°,120°,60°
(9)、120°,90°
(10)B
(11)A
六、课堂小结
学生总结,教师补充
七、家庭作业
1、下列说法错误的是 ( )
A、同角或等角的余角相等 B、同角或等角的补角相等
C、两个锐角的余角相等 D、两个直角的补角相等
2、如果两个锐角的和是 ,则这两个角互为余角,如果两个角的和是 ,则这两个角互为补角。
3、若∠α=50?,则它的余角是 ,它的补角是 。
4、若∠β=110?,则它的补角是 ,它的补角的余角是 。
5、若∠1与∠2互余,∠3和∠2互补,且∠3=120?,那么∠1=
6、已知一个角的补角是这个角的余角的3倍,求这个角。
7.如图,直线AB、CD相交于O,已知∠AOC=75°,OE把∠B OD 分成两部分,且∠BOE:∠EOD=2∶3,求∠AOE。
8.如图,直线CD和∠AOB两边相交于点M、N,已知∠α+∠β=180°。
(1)试找出图中所有与∠α、∠β相等的角;
(2)写出图中所有互补的角。(7分)
9.如图,已知直线AB、CD相交于O,OE、OF分别是∠AOC、∠BOD 的角平分线,射线OE、OF在同一条直线上吗?为什么?(7分)。
10.如图是一个3×3的正方形,求图中∠1+∠2+∠3+...+∠9的和。(8分)
家庭作业答案
1 . C
2 . 90?,180?;
3 .40?, 130?;
4.70?, 20?
5、30?
6、45?
7.设∠BOE=2x,∠EOD=3x
∵∠BOD=∠AOC=75°
∴2x+3x=750
∴x=15°
∴∠DOE=45°
∵∠AOC与∠AOD互补
∴∠AOD=180°-75°=105°
∴∠AOE=∠AOD+∠DOE=105°+45°
=150°
8.(1)与∠α相等的角有3个,
即∠AND,∠BMC,∠OMD
与∠β相等的角也有3个,
即∠BMD,∠OND,∠MNA
(2)图中共有16对角互补
在∠α,∠AND,∠BMC,∠OMD与∠β,∠BMD,∠OND,∠MNA中各取一个都互补
9.OE、OF在同一直线上,理由如下:
∵OE平分∠AOC
∴∠AOE=∠COE
∵OF平分∠BOD
∴∠BOF=∠DOF
∵∠AOC=BOD
∴∠AOE=∠EOC=∠BOF=∠FOD
∴∠EOF=∠EOC+∠COB+∠BOF
=∠COB+∠BOF+∠FOD=∠COD=180°
10.由于沿AB作对折时,图形能够重合,
恰有∠1+∠9=∠2+∠6=∠4+∠8=90 °
∴∠1+∠2+...+∠9
=(∠1+∠9+∠2+∠6)+(∠4+∠8)+(∠3+∠5+ ∠7)
=3×90°+3×45°=405°.毛
年 级: 辅导科目: 数学 课时数:
课 题
角的分类
教学目的
1.余角、补角及对顶角的定义
2.余角、补角及对顶角的性质
教学内容
一、日校回顾
二、上节课知识点回顾
检查上次所留作业
三、知识梳理
1定义:
互为余角的 个角满足的条件:
互为补角的 个角满足的条件:
互为对顶角的 个角满足的条件:
2性质:
的余角相等
的补角相等
对顶角
四、例题讲解
余角的定义和性质
(1)若∠A+∠B=90°,∠B+∠C=90°,则∠A______∠C,理由是_________________;
(2)∠α=50°24′,那么∠α的余角等于____________。毛
(3)、如图,O是直线AB一点,∠BOD=∠COE=90?,
则(a)如果∠1=30?,那么∠2= ,∠3= 。
(b)和∠1互为余角的有 。
和∠1相等的角有 。
(4)∠1与∠2互余,∠1=50°+2°,∠2=4x°-2°,则∠1=______,∠2=______.
(5).下列说法中正确的是( )
A.任何一个角都有余角 B.一个角的余角一定是锐角
C.一个角的余角可能是锐角,也可能是钝角 D. 以上答案都不对
(6)如图,∠ACB=∠CDB=90?,图中∠ACD的余角有 个。
(7)3、如图,∠AOD=∠DOB=∠COE=90?,其中共有互余的角( )
A、2对 B、3对 C、4对 D、6对
(8)、如图,∠AOC=∠BOD=90?,∠AOD=130?,求∠BOC的度数。
补角的定义和性质
(9).已知∠α、∠β互为补角,且∠α=∠β,则∠α=___________。
(10) 若∠1+∠3=180°,∠2+∠4=180°,且∠1=∠2,则∠4_____ ∠3,理由是_______________________。
(11) 下列说法正确的是( )
A.一个角的补角一定大于这个角; B.任何一个角都有补角
C.若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余
D.一个角如有余角,则这个角的补角与它的余角的差为90°
(12)若互补的两个角有一条公共边,则这两个角的平分线所形成的角( )
A.一定是直角 B.一定是锐角 C.一定是钝角 D.是直角或者是锐角
(13)、若∠1与∠2互为补角,且∠1<∠2,则∠1的余角是 ( )
A、∠1 B、∠1+∠2 C、(∠1+∠2) D、(∠2-∠1)
(14)、如图,O是直线BD上一点,∠BOC=36?,∠AOB=108?,
则与∠AOB互补的角有 。
(15)已知一个角的余角比它的补角的4/9还少6?,求这个角
(16)如图,O是直线AB上的一点,OM是∠AOC的角平分线,ON是∠BOC的角平分线,
(1)图中互余的角有几对?
(2)图中互补的角有几对?
对顶角的定义及性质
(17) 下列说法中正确的是( )
A.有公共顶点的角是对顶角 B.相等的角是对顶角
C.对顶角必相等 D.不是对顶角的角不相等
(18)三条线相交于一点,所成的小于平角的对顶角有( )
A.3对 B.4 对 C.5对 D.6对
(19)已知如图,三条直线AB、CD、EF交于一点,若∠1=30°,∠2=70°,求∠3的度数。
例题讲解答案:
(1)=, 同角的余角相等
(2) 39°36′
(3)(a) 60?,30?(b)∠2∠4,∠3;
(4)52°,38°
(5)B
(6)2
(7)C
(8)50 ?
(9)90°
(10)=,等角的补角相等
(11)D
(12)D
(13)D
(14)∠ AOD,∠AOC
(15)28.8?
(16) 4 、 5
(17)C
(18)D
(19)∵直线AB、CD、DF交于一点
∴2∠1+2∠2+2∠3=360°
∴∠1+∠2+∠3=180°
又∵∠1=30,∠2=70°
∴∠3=180°-∠1-∠2=80°
五、课堂练习
(1)∠1与∠2互余,∠1=(6x+8)?,∠2=(4x-8)?,则∠1= ,∠2=
(2)已知互余两个角的差是30?,则这两个角的度数分别是________________。
(3)16.如图4,ACB是直线,AB⊥CD,EC⊥FC,图中共有( )对角互余
A.2 B.3 C.4 D.以上都不对
(4)一个锐角的补角比这个角的余角大 ( )
A、30? B、45? C、60? D、90?
(5)一个角的补角是 ( )
A、锐角 B、直角 C、钝角 D、以上三种情况都有可能
(6)、若∠1与∠2互补,∠3与∠1互余,∠2+∠3=240?,由∠2是∠1的 ( )
A、2倍 B、5倍 C、11倍 D、无法确定倍数
(7)若∠1和∠2互余,∠2 和∠3 互补,∠1=63°,则∠3 =________.
(8)如图1,直线AB和CD相交于点O,∠DOE是直角,若∠1=30°,则∠2=________,∠3=________。∠4=__________。
(9)如图2,直线a、b、c两两相交,∠1=60°,∠2=false∠4,则∠3=_____,∠5=_______。
(10) 若一个角的补角是这个角的余角的3倍,则这个角是( )
A.30° B.45° C.60° D.75°
(11).如图,∠1>∠2,那么∠2与false(∠1-∠2)之间的关系是( )
A.互余 B.互补 C.和为45° D.22.5°
课堂练习答案
(1) 58? ,32?,
(2)60?,30?
(3)C
(4)D
(5)D
(6)C
(7)153°
(8)60°,120°,60°
(9)、120°,90°
(10)B
(11)A
六、课堂小结
学生总结,教师补充
七、家庭作业
1、下列说法错误的是 ( )
A、同角或等角的余角相等 B、同角或等角的补角相等
C、两个锐角的余角相等 D、两个直角的补角相等
2、如果两个锐角的和是 ,则这两个角互为余角,如果两个角的和是 ,则这两个角互为补角。
3、若∠α=50?,则它的余角是 ,它的补角是 。
4、若∠β=110?,则它的补角是 ,它的补角的余角是 。
5、若∠1与∠2互余,∠3和∠2互补,且∠3=120?,那么∠1=
6、已知一个角的补角是这个角的余角的3倍,求这个角。
7.如图,直线AB、CD相交于O,已知∠AOC=75°,OE把∠B OD 分成两部分,且∠BOE:∠EOD=2∶3,求∠AOE。
8.如图,直线CD和∠AOB两边相交于点M、N,已知∠α+∠β=180°。
(1)试找出图中所有与∠α、∠β相等的角;
(2)写出图中所有互补的角。(7分)
9.如图,已知直线AB、CD相交于O,OE、OF分别是∠AOC、∠BOD 的角平分线,射线OE、OF在同一条直线上吗?为什么?(7分)。
10.如图是一个3×3的正方形,求图中∠1+∠2+∠3+...+∠9的和。(8分)
家庭作业答案
1 . C
2 . 90?,180?;
3 .40?, 130?;
4.70?, 20?
5、30?
6、45?
7.设∠BOE=2x,∠EOD=3x
∵∠BOD=∠AOC=75°
∴2x+3x=750
∴x=15°
∴∠DOE=45°
∵∠AOC与∠AOD互补
∴∠AOD=180°-75°=105°
∴∠AOE=∠AOD+∠DOE=105°+45°
=150°
8.(1)与∠α相等的角有3个,
即∠AND,∠BMC,∠OMD
与∠β相等的角也有3个,
即∠BMD,∠OND,∠MNA
(2)图中共有16对角互补
在∠α,∠AND,∠BMC,∠OMD与∠β,∠BMD,∠OND,∠MNA中各取一个都互补
9.OE、OF在同一直线上,理由如下:
∵OE平分∠AOC
∴∠AOE=∠COE
∵OF平分∠BOD
∴∠BOF=∠DOF
∵∠AOC=BOD
∴∠AOE=∠EOC=∠BOF=∠FOD
∴∠EOF=∠EOC+∠COB+∠BOF
=∠COB+∠BOF+∠FOD=∠COD=180°
10.由于沿AB作对折时,图形能够重合,
恰有∠1+∠9=∠2+∠6=∠4+∠8=90 °
∴∠1+∠2+...+∠9
=(∠1+∠9+∠2+∠6)+(∠4+∠8)+(∠3+∠5+ ∠7)
=3×90°+3×45°=405°.毛
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
