第01讲 丰富的图形世界 讲义(含答案)
文档属性
| 名称 | 第01讲 丰富的图形世界 讲义(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 250.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 15:47:08 | ||
图片预览

文档简介
教师讲义
年 级: 辅导科目: 数学 课时数:
课 题
丰富的图形世界
教学目的
会画基本几何体的三视图,能根据三视图描述基本几何体或实物原型;
了解直棱柱、圆锥的侧面展开图,能根据展开图判断和制作立体模形;
了解基本几何体的展开图、三视图间的关系,通过实例,知道这种关系在现实生活中的应用.
教学内容
日校回顾
上节课知识回顾及作业检查
知识点梳理
(一)常见的立体图形
1.柱体有_______、________、_________和__________.
2.锥体有_______和________.
3.台体有_______和________.
4.球体
(二)部分几何体的平面展开图.
1.圆柱的表面展开图是_________(作底面)和_________(作侧面).
2.圆锥的表面展开图是_________(作底面)和_________(作侧面).
3.棱柱的表面展开图是_________(作底面)和_________(作侧面)
(三)正方体的十一种展开图.(动手画)
(四)截一个几何体
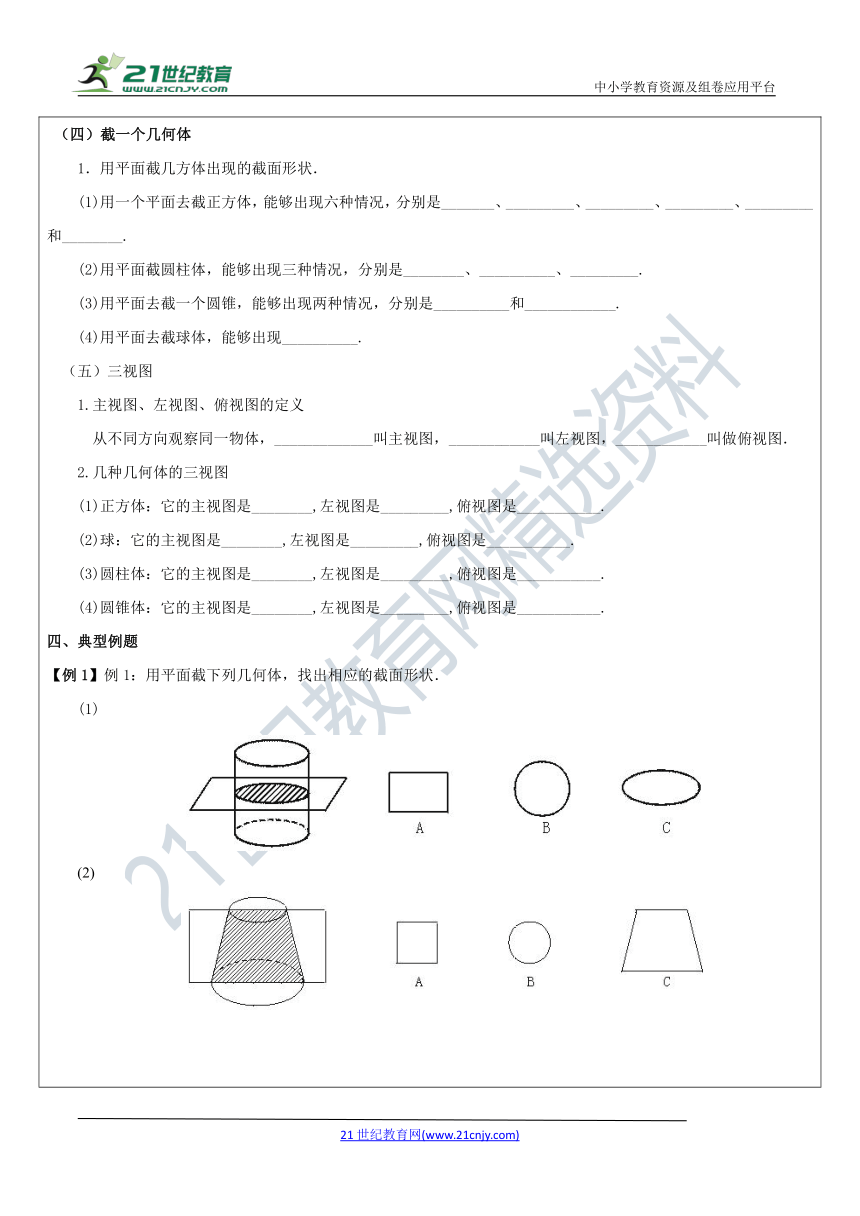
1.用平面截几方体出现的截面形状.
(1)用一个平面去截正方体,能够出现六种情况,分别是_______、_________、_________、_________、_________和________.
(2)用平面截圆柱体,能够出现三种情况,分别是________、__________、_________.
(3)用平面去截一个圆锥,能够出现两种情况,分别是__________和____________.
(4)用平面去截球体,能够出现__________.
(五)三视图
1.主视图、左视图、俯视图的定义
从不同方向观察同一物体,_____________叫主视图,____________叫左视图,____________叫做俯视图.
2.几种几何体的三视图
(1)正方体:它的主视图是________,左视图是_________,俯视图是___________.
(2)球:它的主视图是________,左视图是_________,俯视图是___________.
(3)圆柱体:它的主视图是________,左视图是_________,俯视图是___________.
(4)圆锥体:它的主视图是________,左视图是_________,俯视图是___________.
典型例题
【例1】例1:用平面截下列几何体,找出相应的截面形状.
(1)
false
(2)
false
(3)
false
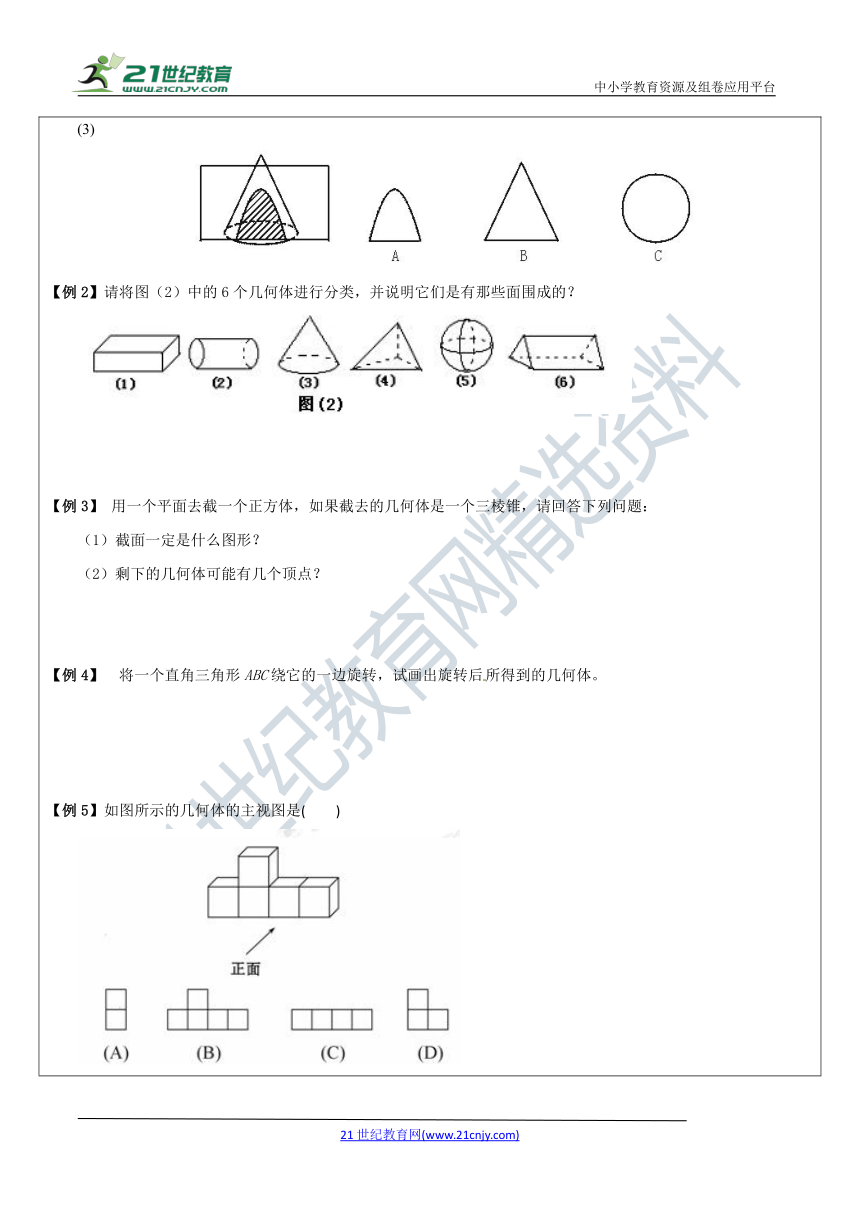
【例2】请将图(2)中的6个几何体进行分类,并说明它们是有那些面围成的?
[
【例3】 用一个平面去截一个正方体,如果截去的几何体是一个三棱锥,请回答下列问题:
(1)截面一定是什么图形?
(2)剩下的几何体可能有几个顶点?
【例4】 将一个直角三角形ABC绕它的一边旋转,试画出旋转后所得到的几何体。
【例5】如图所示的几何体的主视图是( )
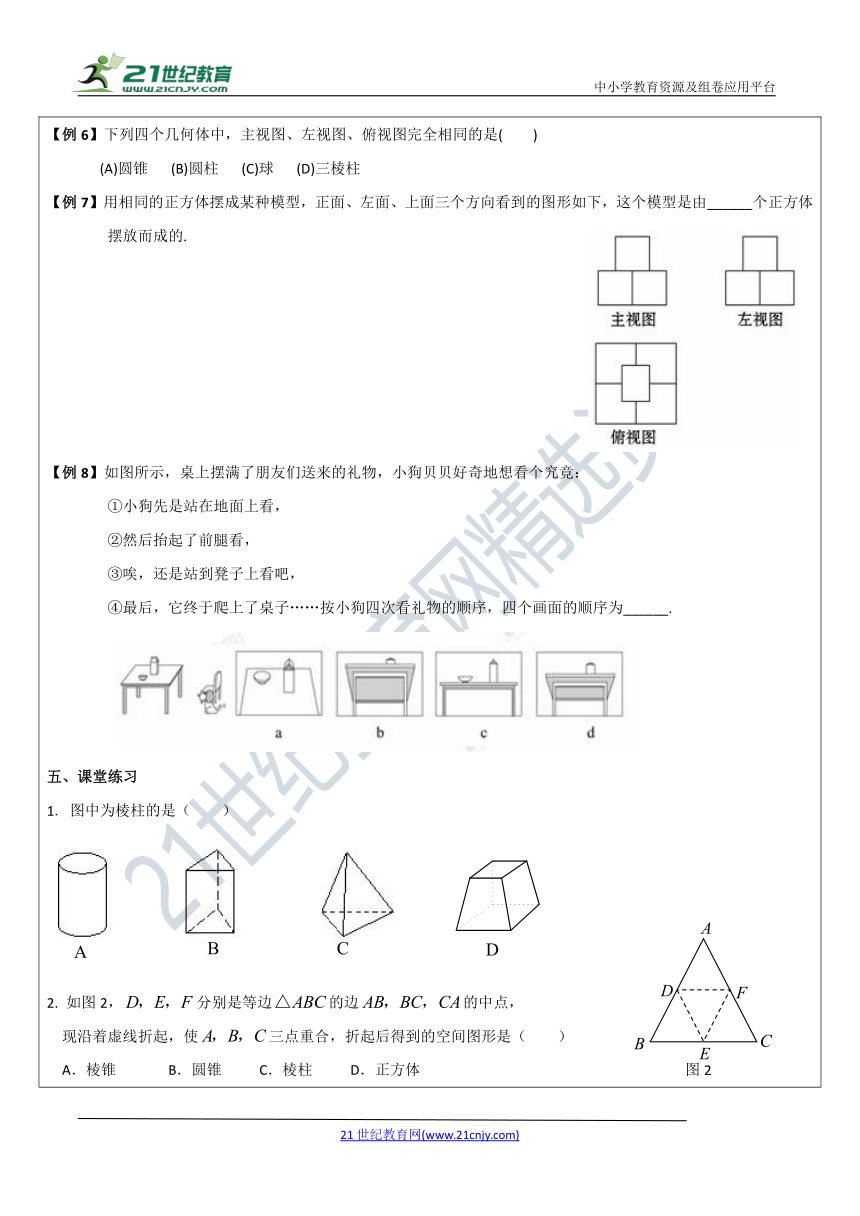
【例6】下列四个几何体中,主视图、左视图、俯视图完全相同的是( )
(A)圆锥 (B)圆柱 (C)球 (D)三棱柱
【例7】用相同的正方体摆成某种模型,正面、左面、上面三个方向看到的图形如下,这个模型是由______个正方体
摆放而成的.
【例8】如图所示,桌上摆满了朋友们送来的礼物,小狗贝贝好奇地想看个究竟:
①小狗先是站在地面上看,
②然后抬起了前腿看,
③唉,还是站到凳子上看吧,
④最后,它终于爬上了桌子……按小狗四次看礼物的顺序,四个画面的顺序为______.
课堂练习
1. 图中为棱柱的是( )
false
false
false
false
false
false
图2
2. 如图2,false分别是等边false的边false的中点,
现沿着虚线折起,使false三点重合,折起后得到的空间图形是( )
A.棱锥 B.圆锥 C.棱柱 D.正方体
3.下面四个图形中,经过折叠能围成如图3只有三个面上印有图案的正方体纸盒的是( )
A.
B.
D.
图3
C.
4. 圆锥侧面展开图可能是下列图中的( )
A.
B.
C.
D.
5.如图4,六棱柱的正确截面是( )
A B C D
6. 圆柱体是由____个面围成,这些面相交共得_____条线,它们是 线.
7. 用一个平面去截某一几何体,若截面是圆,则原来的几何体可能是 .
8. 将半圆绕直径旋转一周,形成的几何体是_______;将直角三角形以一条直角边为轴旋转一周,形成的几何体是________;假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了_______ ___.
9. 如果一个几何体的主视图、左视图、俯视图都完全相同的是 .
10. 如果长方体从一顶点出发的三条棱长分别为2,3,4,则该长方体的表面积为______,体积为____ __.
我
喜
欢
数
学
课
图9
11.如图9,这是一个正方开体的展开图,则“喜”代表的面所相对的面的号码是 .
12.将下列几何体分类,并说明理由(分类标准).
主视图
左视图
俯视图
13.画出下列几何体的三视图.
主视图
左视图
14.如图所示是由几个小正方体组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图和左视图.
六、课堂小结:
七、课后作业:
1.下列说法中,正确的个数是( ).
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
(A)2个 (B)3个 (C)4个 (D)5个
2. 下面几何体截面一定是圆的是 ( )
( A)圆柱 (B) 圆锥 (C) 球 (D) 圆台
3.如图绕虚线旋转得到的几何体是( ).
4. 某物体的三视图是如图所示的三个图形,那么该物体的形状是( )
(A)长方体 ( B)圆锥体
(C)立方体 (D)圆柱体
5.如图,其主视图是(?? )
6.正方体与长方体的相同点是_________________,不同点是_______________。
7.点动成_____,线动成_____,_____动成体。比如:(1)圆规在纸上划过会留下一个封闭的痕迹,这种现象说明_________。(2)冬天环卫工人使用下部是长方形的木锨推雪时,木锨过处,雪就没了,这种现象说明________。(3)一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快地旋转起来时就会看到一个球,这种现象说明______________。
8.谜语:正看三条边,侧看三条边,上看圆圈圈,就是没直边。(打一几何体)________。
9. 桌面上放两件物体,它们的三视图如下图示,则这两个物体分别是________.
主视图 俯视图 左视图
10.画出下面几何体的主视图、左视图与俯视图.
11. 如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图。
2
3
4
2
1
1
12.如图是由几个小立方块所搭几何体的俯视图和左视图,请再根据它画出主视图。
左视图
俯视图
附答案:
例题:
例1:(1)B (2)C (3)A
例2:解:图(2)中的(1)、(2)、(6)是柱体。其中(1)是长方体,它有6个长方形的平面围成;(2)是圆柱体,它有2个圆和一个曲面围成;(6)是棱柱体,它有2个三角形平面和三个长方形平面围成。(3)、(4)是锥体。其中(3)是圆锥体,它有一个圆和一个曲面围成;(4)是棱锥体,它有四个三角形平面围成。(6)是球体。它只有一个曲面围成。
例3:解:(1)如果截去的几何体是一个三棱锥,那么截面一定是一个三角形.
(2)剩下的几何体可能有7个、或8个、或9个、或10个,如图(3)所示.
例4:解:如图(4)分别沿三条边旋转一周,得到如图(5)所示的三个几何体:
例5:B 例6:C 例7:5个 例8:bdca
课堂练习:
1.B 2.A 3.B 4.D 5.B
6.3,2,曲; 7.球、圆柱或圆锥; 8.球,圆锥,点动成线 ; 9.球体或正方体 10.52,24; 11.学
12.按柱、锥、球分:柱体:(1)(2)(3);锥体:(5)(6); 球体:(4)
或按组成的面平或曲来分:组成的面都是平面(1)(3)(6);组成的面有曲面(2)(4)(6);
图略. 14.图略.
课后作业:
C 2、C 3、D 4、D 5、B
6、相同点:都是四棱柱、有六个面、十二个顶点、十二条棱;
不同点:正方体的六个面都是大小相同的正方形、长方体的六个面是大小不尽相同的长方形;
7、线、面、面 ①点动成线 ②线动成面 ③面动成体 8、圆锥 9、圆柱和四棱柱
主视图
左视图
10、略11、 12、主视图
主视图
年 级: 辅导科目: 数学 课时数:
课 题
丰富的图形世界
教学目的
会画基本几何体的三视图,能根据三视图描述基本几何体或实物原型;
了解直棱柱、圆锥的侧面展开图,能根据展开图判断和制作立体模形;
了解基本几何体的展开图、三视图间的关系,通过实例,知道这种关系在现实生活中的应用.
教学内容
日校回顾
上节课知识回顾及作业检查
知识点梳理
(一)常见的立体图形
1.柱体有_______、________、_________和__________.
2.锥体有_______和________.
3.台体有_______和________.
4.球体
(二)部分几何体的平面展开图.
1.圆柱的表面展开图是_________(作底面)和_________(作侧面).
2.圆锥的表面展开图是_________(作底面)和_________(作侧面).
3.棱柱的表面展开图是_________(作底面)和_________(作侧面)
(三)正方体的十一种展开图.(动手画)
(四)截一个几何体
1.用平面截几方体出现的截面形状.
(1)用一个平面去截正方体,能够出现六种情况,分别是_______、_________、_________、_________、_________和________.
(2)用平面截圆柱体,能够出现三种情况,分别是________、__________、_________.
(3)用平面去截一个圆锥,能够出现两种情况,分别是__________和____________.
(4)用平面去截球体,能够出现__________.
(五)三视图
1.主视图、左视图、俯视图的定义
从不同方向观察同一物体,_____________叫主视图,____________叫左视图,____________叫做俯视图.
2.几种几何体的三视图
(1)正方体:它的主视图是________,左视图是_________,俯视图是___________.
(2)球:它的主视图是________,左视图是_________,俯视图是___________.
(3)圆柱体:它的主视图是________,左视图是_________,俯视图是___________.
(4)圆锥体:它的主视图是________,左视图是_________,俯视图是___________.
典型例题
【例1】例1:用平面截下列几何体,找出相应的截面形状.
(1)
false
(2)
false
(3)
false
【例2】请将图(2)中的6个几何体进行分类,并说明它们是有那些面围成的?
[
【例3】 用一个平面去截一个正方体,如果截去的几何体是一个三棱锥,请回答下列问题:
(1)截面一定是什么图形?
(2)剩下的几何体可能有几个顶点?
【例4】 将一个直角三角形ABC绕它的一边旋转,试画出旋转后所得到的几何体。
【例5】如图所示的几何体的主视图是( )
【例6】下列四个几何体中,主视图、左视图、俯视图完全相同的是( )
(A)圆锥 (B)圆柱 (C)球 (D)三棱柱
【例7】用相同的正方体摆成某种模型,正面、左面、上面三个方向看到的图形如下,这个模型是由______个正方体
摆放而成的.
【例8】如图所示,桌上摆满了朋友们送来的礼物,小狗贝贝好奇地想看个究竟:
①小狗先是站在地面上看,
②然后抬起了前腿看,
③唉,还是站到凳子上看吧,
④最后,它终于爬上了桌子……按小狗四次看礼物的顺序,四个画面的顺序为______.
课堂练习
1. 图中为棱柱的是( )
false
false
false
false
false
false
图2
2. 如图2,false分别是等边false的边false的中点,
现沿着虚线折起,使false三点重合,折起后得到的空间图形是( )
A.棱锥 B.圆锥 C.棱柱 D.正方体
3.下面四个图形中,经过折叠能围成如图3只有三个面上印有图案的正方体纸盒的是( )
A.
B.
D.
图3
C.
4. 圆锥侧面展开图可能是下列图中的( )
A.
B.
C.
D.
5.如图4,六棱柱的正确截面是( )
A B C D
6. 圆柱体是由____个面围成,这些面相交共得_____条线,它们是 线.
7. 用一个平面去截某一几何体,若截面是圆,则原来的几何体可能是 .
8. 将半圆绕直径旋转一周,形成的几何体是_______;将直角三角形以一条直角边为轴旋转一周,形成的几何体是________;假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了_______ ___.
9. 如果一个几何体的主视图、左视图、俯视图都完全相同的是 .
10. 如果长方体从一顶点出发的三条棱长分别为2,3,4,则该长方体的表面积为______,体积为____ __.
我
喜
欢
数
学
课
图9
11.如图9,这是一个正方开体的展开图,则“喜”代表的面所相对的面的号码是 .
12.将下列几何体分类,并说明理由(分类标准).
主视图
左视图
俯视图
13.画出下列几何体的三视图.
主视图
左视图
14.如图所示是由几个小正方体组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图和左视图.
六、课堂小结:
七、课后作业:
1.下列说法中,正确的个数是( ).
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
(A)2个 (B)3个 (C)4个 (D)5个
2. 下面几何体截面一定是圆的是 ( )
( A)圆柱 (B) 圆锥 (C) 球 (D) 圆台
3.如图绕虚线旋转得到的几何体是( ).
4. 某物体的三视图是如图所示的三个图形,那么该物体的形状是( )
(A)长方体 ( B)圆锥体
(C)立方体 (D)圆柱体
5.如图,其主视图是(?? )
6.正方体与长方体的相同点是_________________,不同点是_______________。
7.点动成_____,线动成_____,_____动成体。比如:(1)圆规在纸上划过会留下一个封闭的痕迹,这种现象说明_________。(2)冬天环卫工人使用下部是长方形的木锨推雪时,木锨过处,雪就没了,这种现象说明________。(3)一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快地旋转起来时就会看到一个球,这种现象说明______________。
8.谜语:正看三条边,侧看三条边,上看圆圈圈,就是没直边。(打一几何体)________。
9. 桌面上放两件物体,它们的三视图如下图示,则这两个物体分别是________.
主视图 俯视图 左视图
10.画出下面几何体的主视图、左视图与俯视图.
11. 如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图。
2
3
4
2
1
1
12.如图是由几个小立方块所搭几何体的俯视图和左视图,请再根据它画出主视图。
左视图
俯视图
附答案:
例题:
例1:(1)B (2)C (3)A
例2:解:图(2)中的(1)、(2)、(6)是柱体。其中(1)是长方体,它有6个长方形的平面围成;(2)是圆柱体,它有2个圆和一个曲面围成;(6)是棱柱体,它有2个三角形平面和三个长方形平面围成。(3)、(4)是锥体。其中(3)是圆锥体,它有一个圆和一个曲面围成;(4)是棱锥体,它有四个三角形平面围成。(6)是球体。它只有一个曲面围成。
例3:解:(1)如果截去的几何体是一个三棱锥,那么截面一定是一个三角形.
(2)剩下的几何体可能有7个、或8个、或9个、或10个,如图(3)所示.
例4:解:如图(4)分别沿三条边旋转一周,得到如图(5)所示的三个几何体:
例5:B 例6:C 例7:5个 例8:bdca
课堂练习:
1.B 2.A 3.B 4.D 5.B
6.3,2,曲; 7.球、圆柱或圆锥; 8.球,圆锥,点动成线 ; 9.球体或正方体 10.52,24; 11.学
12.按柱、锥、球分:柱体:(1)(2)(3);锥体:(5)(6); 球体:(4)
或按组成的面平或曲来分:组成的面都是平面(1)(3)(6);组成的面有曲面(2)(4)(6);
图略. 14.图略.
课后作业:
C 2、C 3、D 4、D 5、B
6、相同点:都是四棱柱、有六个面、十二个顶点、十二条棱;
不同点:正方体的六个面都是大小相同的正方形、长方体的六个面是大小不尽相同的长方形;
7、线、面、面 ①点动成线 ②线动成面 ③面动成体 8、圆锥 9、圆柱和四棱柱
主视图
左视图
10、略11、 12、主视图
主视图
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
