科学命题同步练习之24.3 正多边形和圆(含解析)
文档属性
| 名称 | 科学命题同步练习之24.3 正多边形和圆(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 536.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
科学命题同步练习之24.3正多边形和圆
一、选择题
已知正六边形的边长为
,则它的内切圆的半径为
A.
B.
C.
D.
如图,
是正五边形
的外接圆,则正五边形的中心角
的度数是
A.
B.
C.
D.
如图,边长为
的正五边形
,顶点
,
在半径为
的圆上,其他各点在圆内,将正五边形
绕点
逆时针旋转,当点
第一次落在圆上时,则点
转过的度数为
A.
B.
C.
D.
如图,在圆内接正六边形
中,,
分别交
于点
,.若该圆的半径为
,则线段
的长为
A.
B.
C.
D.
下列是关于四个图案的描述.
图
所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称;
图
所示是一个正三角形内接于圆;
图
所示是一个正方形内接于圆;
图
所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二.
这四个图案中,阴影部分的面积不小于该图案外圈大圆面积一半的是
A.图
和图
B.图
和图
C.图
和图
D.图
和图
尺规作图特有的魅力曾使无数人沉湎其中,传说拿破仑通过下列尺规作图考他的大臣:
①将半径为
的
六等分,依次得到
,,,,,
六个分点;
②分别以点
,
为圆心,
长为半径画弧,
是两弧的一个交点;
③连接
.
问:
的长是多少?
大臣给出的正确答案应是
A.
B.
C.
D.
二、填空题
同一个圆的内接正方形和正三角形的内切圆半径比为
.
有一个边长为
的正方形,若要剪一张圆形纸片完全盖住这个正方形,则这个圆形纸片的半径最小是
.
颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为
米的正六边形,那么这个地基的面积是
.
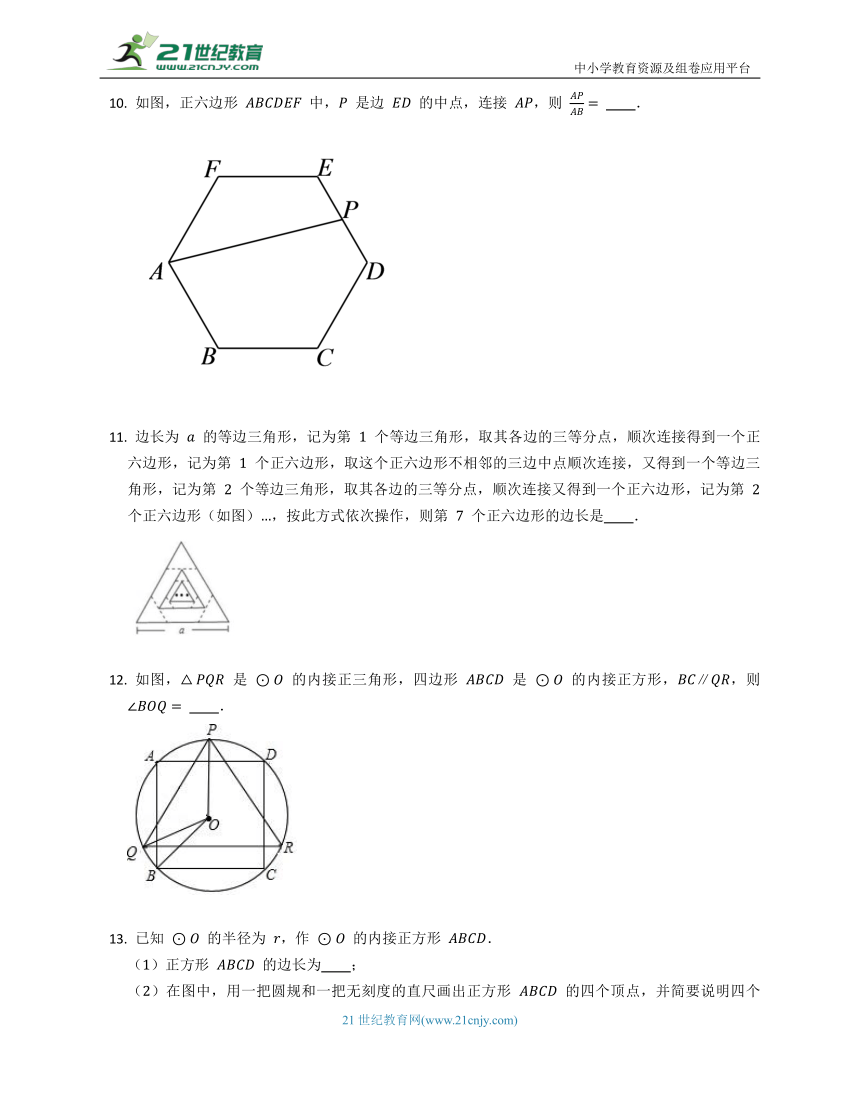
如图,正六边形
中,
是边
的中点,连接
,则
.
边长为
的等边三角形,记为第
个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第
个正六边形,取这个正六边形不相邻的三边中点顺次连接,又得到一个等边三角形,记为第
个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第
个正六边形(如图),按此方式依次操作,则第
个正六边形的边长是
.
如图,
是
的内接正三角形,四边形
是
的内接正方形,,则
.
已知
的半径为
,作
的内接正方形
.
()正方形
的边长为
;
()在图中,用一把圆规和一把无刻度的直尺画出正方形
的四个顶点,并简要说明四个顶点的位置是如何找到的(不要求证明)
.
三、解答题
如图,在
中,,,点
在边
上,且
,
平分
.
(1)
求
和
的度数.
(2)
以
为边,在
的左侧作正五边形
,求
的度数.
如图,已知正三角形
内接于
,
是
的内接正十二边形的一条边长,连接
,若
,求
的半径.
用圆规可以作出许多美丽的图案,传说拿破仑曾考他的大臣:只用圆规把圆四等分.有位大臣是这样回答的:
①将半径为
的
六等分,依次得到
,,,,,
六个分点;
②分别以点
,
为圆心,
长为半径画弧
是两弧的一个交点;
③
.
(1)
根据大臣的作法,
的长是多少.
(2)
请在图
中,只用圆规把圆四等分.(不写作法,保留作图痕迹)
答案
一、选择题
1.
【答案】B
【解析】由题意得,,
,
.
【知识点】正多边形与圆
2.
【答案】A
【解析】
是正五边形
的外接圆,
.
【知识点】正多边形与圆
3.
【答案】A
【解析】设点
第一次落在圆上时的对应点为
,连接
,,,如图,
五边形
为正五边形,
,
正五边形
绕点
逆时针旋转,点
第一次落在圆上
点,
,
,
,
都为等边三角形,
,
,
,
当点
第一次落在圆上时,则点
转过的度数为
.
【知识点】正多边形与圆、旋转及其性质
4.
【答案】B
【解析】
在圆内接正六边形
中,,
,
,
,,
,
,
连接
,,
交
于
,
则
,,
,
,
,
.
【知识点】解直角三角形、正多边形与圆、等腰三角形的判定
5.
【答案】A
【解析】设外圈大圆的半径为
,则外圈大圆的面积
,
图
所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称,
阴影部分的面积
大圆面积一半;
图
所示是一个正三角形的面积
;
图
所示是一个正方形的面积
;
图
所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二,
小圆的面积
,
故选:A.
【知识点】正多边形与圆
6.
【答案】D
【知识点】正多边形与圆
二、填空题
7.
【答案】
【解析】设
的半径为
,
的内接正方形
,
如图,过
作
于
,连接
,,
即
为正方形
的边心距,
四边形
是正方形,
是正方形
的外接圆,
为正方形
的中心,
,
,,
,,
,
设
的内接正
,
如图,过
作
于
,连接
,
即
为正
的边心距,
正
是
的外接圆,
,
,
.
【知识点】正多边形与圆
8.
【答案】
【知识点】正多边形与圆
9.
【答案】
【解析】如图所示,连接
,,过点
作
于
.
六边形
是正六边形,
.
,
是等边三角形.
.
.
.
.
【知识点】正多边形与圆
10.
【答案】
【解析】如图,连接
,设
,
正六边形
,
,
为等腰三角形,
,,,
,
,
.
【知识点】正多边形与圆、勾股定理、30度所对的直角边等于斜边的一半
11.
【答案】
【解析】如图
,连接
,,.
六边形
是正六边形,
,,,,
,
,
,
在
和
中,
,
,
,
,
,
分别为
,
中点,
,
,
六边形
是正六边形,
是等边三角形,
,
,
同理
,
即
,
等边三角形
的边长是
,
第一个正六边形
的边长是
,即等边三角形
的边长的
.
如图
,过
作
于
,过
作
于
,
则
,
,
四边形
是平行四边形,
,
,(已证),
,
,
同理
,
,即第二个等边三角形的边长是
,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是
;
同理第第三个等边三角形的边长是
,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是
;
同理第四个等边三角形的边长是
,第四个正六边形的边长是
;
第五个等边三角形的边长是
,第五个正六边形的边长是
;
第
个正六边形的边长是
,
第七个正六边形的边长是
.
【知识点】正多边形与圆、平行四边形的判定、用代数式表示规律、斜边、直角边
12.
【答案】
【解析】连接
,,
是
的内接正三角形,
,
,
,,
,
,
四边形
是
的内接正方形,
,,
,
,
,
.
,
.
【知识点】弧、弦、圆心角的关系定理、正多边形与圆
13.
【答案】;如图所示:
作法:①以圆上任意一点
为圆心,以
为半径画圆,交
于
和
,
②以
为圆心,以
为半径画圆,与
交于
和
,与
交于另一点
,
③作直线
,交
于
,,顺次连接
,,,,四边形
即为所求.
【知识点】尺规作图原理、正多边形与圆
三、解答题
14.
【答案】
(1)
在
中,
,,
,
,
,
,
平分
,
,
,
综上可知,
的度数为
,
的度数为
.
(2)
五边形
是正五边形,
正五边形
的内角和为
,
,
,
即
的度数为
.
【知识点】三角形的内角和、多边形的内外角和、正多边形与圆
15.
【答案】连接
,,,如图所示:
等边
内接于
,
为内接正十二边形的一边,
,,
,
,
是等腰直角三角形,
,
即
的半径为
.
【知识点】等腰直角三角形、正多边形与圆
16.
【答案】
(1)
由题意知:,,
,
,
故答案为:.
(2)
以
为圆心,
为半径作弧交
于点
,,即
,,,
为
的四分点.
【知识点】勾股定理、正多边形与圆
21世纪教育网(www.21cnjy.com)
科学命题同步练习之24.3正多边形和圆
一、选择题
已知正六边形的边长为
,则它的内切圆的半径为
A.
B.
C.
D.
如图,
是正五边形
的外接圆,则正五边形的中心角
的度数是
A.
B.
C.
D.
如图,边长为
的正五边形
,顶点
,
在半径为
的圆上,其他各点在圆内,将正五边形
绕点
逆时针旋转,当点
第一次落在圆上时,则点
转过的度数为
A.
B.
C.
D.
如图,在圆内接正六边形
中,,
分别交
于点
,.若该圆的半径为
,则线段
的长为
A.
B.
C.
D.
下列是关于四个图案的描述.
图
所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称;
图
所示是一个正三角形内接于圆;
图
所示是一个正方形内接于圆;
图
所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二.
这四个图案中,阴影部分的面积不小于该图案外圈大圆面积一半的是
A.图
和图
B.图
和图
C.图
和图
D.图
和图
尺规作图特有的魅力曾使无数人沉湎其中,传说拿破仑通过下列尺规作图考他的大臣:
①将半径为
的
六等分,依次得到
,,,,,
六个分点;
②分别以点
,
为圆心,
长为半径画弧,
是两弧的一个交点;
③连接
.
问:
的长是多少?
大臣给出的正确答案应是
A.
B.
C.
D.
二、填空题
同一个圆的内接正方形和正三角形的内切圆半径比为
.
有一个边长为
的正方形,若要剪一张圆形纸片完全盖住这个正方形,则这个圆形纸片的半径最小是
.
颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为
米的正六边形,那么这个地基的面积是
.
如图,正六边形
中,
是边
的中点,连接
,则
.
边长为
的等边三角形,记为第
个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第
个正六边形,取这个正六边形不相邻的三边中点顺次连接,又得到一个等边三角形,记为第
个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第
个正六边形(如图),按此方式依次操作,则第
个正六边形的边长是
.
如图,
是
的内接正三角形,四边形
是
的内接正方形,,则
.
已知
的半径为
,作
的内接正方形
.
()正方形
的边长为
;
()在图中,用一把圆规和一把无刻度的直尺画出正方形
的四个顶点,并简要说明四个顶点的位置是如何找到的(不要求证明)
.
三、解答题
如图,在
中,,,点
在边
上,且
,
平分
.
(1)
求
和
的度数.
(2)
以
为边,在
的左侧作正五边形
,求
的度数.
如图,已知正三角形
内接于
,
是
的内接正十二边形的一条边长,连接
,若
,求
的半径.
用圆规可以作出许多美丽的图案,传说拿破仑曾考他的大臣:只用圆规把圆四等分.有位大臣是这样回答的:
①将半径为
的
六等分,依次得到
,,,,,
六个分点;
②分别以点
,
为圆心,
长为半径画弧
是两弧的一个交点;
③
.
(1)
根据大臣的作法,
的长是多少.
(2)
请在图
中,只用圆规把圆四等分.(不写作法,保留作图痕迹)
答案
一、选择题
1.
【答案】B
【解析】由题意得,,
,
.
【知识点】正多边形与圆
2.
【答案】A
【解析】
是正五边形
的外接圆,
.
【知识点】正多边形与圆
3.
【答案】A
【解析】设点
第一次落在圆上时的对应点为
,连接
,,,如图,
五边形
为正五边形,
,
正五边形
绕点
逆时针旋转,点
第一次落在圆上
点,
,
,
,
都为等边三角形,
,
,
,
当点
第一次落在圆上时,则点
转过的度数为
.
【知识点】正多边形与圆、旋转及其性质
4.
【答案】B
【解析】
在圆内接正六边形
中,,
,
,
,,
,
,
连接
,,
交
于
,
则
,,
,
,
,
.
【知识点】解直角三角形、正多边形与圆、等腰三角形的判定
5.
【答案】A
【解析】设外圈大圆的半径为
,则外圈大圆的面积
,
图
所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称,
阴影部分的面积
大圆面积一半;
图
所示是一个正三角形的面积
;
图
所示是一个正方形的面积
;
图
所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二,
小圆的面积
,
故选:A.
【知识点】正多边形与圆
6.
【答案】D
【知识点】正多边形与圆
二、填空题
7.
【答案】
【解析】设
的半径为
,
的内接正方形
,
如图,过
作
于
,连接
,,
即
为正方形
的边心距,
四边形
是正方形,
是正方形
的外接圆,
为正方形
的中心,
,
,,
,,
,
设
的内接正
,
如图,过
作
于
,连接
,
即
为正
的边心距,
正
是
的外接圆,
,
,
.
【知识点】正多边形与圆
8.
【答案】
【知识点】正多边形与圆
9.
【答案】
【解析】如图所示,连接
,,过点
作
于
.
六边形
是正六边形,
.
,
是等边三角形.
.
.
.
.
【知识点】正多边形与圆
10.
【答案】
【解析】如图,连接
,设
,
正六边形
,
,
为等腰三角形,
,,,
,
,
.
【知识点】正多边形与圆、勾股定理、30度所对的直角边等于斜边的一半
11.
【答案】
【解析】如图
,连接
,,.
六边形
是正六边形,
,,,,
,
,
,
在
和
中,
,
,
,
,
,
分别为
,
中点,
,
,
六边形
是正六边形,
是等边三角形,
,
,
同理
,
即
,
等边三角形
的边长是
,
第一个正六边形
的边长是
,即等边三角形
的边长的
.
如图
,过
作
于
,过
作
于
,
则
,
,
四边形
是平行四边形,
,
,(已证),
,
,
同理
,
,即第二个等边三角形的边长是
,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是
;
同理第第三个等边三角形的边长是
,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是
;
同理第四个等边三角形的边长是
,第四个正六边形的边长是
;
第五个等边三角形的边长是
,第五个正六边形的边长是
;
第
个正六边形的边长是
,
第七个正六边形的边长是
.
【知识点】正多边形与圆、平行四边形的判定、用代数式表示规律、斜边、直角边
12.
【答案】
【解析】连接
,,
是
的内接正三角形,
,
,
,,
,
,
四边形
是
的内接正方形,
,,
,
,
,
.
,
.
【知识点】弧、弦、圆心角的关系定理、正多边形与圆
13.
【答案】;如图所示:
作法:①以圆上任意一点
为圆心,以
为半径画圆,交
于
和
,
②以
为圆心,以
为半径画圆,与
交于
和
,与
交于另一点
,
③作直线
,交
于
,,顺次连接
,,,,四边形
即为所求.
【知识点】尺规作图原理、正多边形与圆
三、解答题
14.
【答案】
(1)
在
中,
,,
,
,
,
,
平分
,
,
,
综上可知,
的度数为
,
的度数为
.
(2)
五边形
是正五边形,
正五边形
的内角和为
,
,
,
即
的度数为
.
【知识点】三角形的内角和、多边形的内外角和、正多边形与圆
15.
【答案】连接
,,,如图所示:
等边
内接于
,
为内接正十二边形的一边,
,,
,
,
是等腰直角三角形,
,
即
的半径为
.
【知识点】等腰直角三角形、正多边形与圆
16.
【答案】
(1)
由题意知:,,
,
,
故答案为:.
(2)
以
为圆心,
为半径作弧交
于点
,,即
,,,
为
的四分点.
【知识点】勾股定理、正多边形与圆
21世纪教育网(www.21cnjy.com)
同课章节目录
