苏科版数学九年级上册2.4圆周角 课件(共24张PPT)
文档属性
| 名称 | 苏科版数学九年级上册2.4圆周角 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 778.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
一.
复习引入:
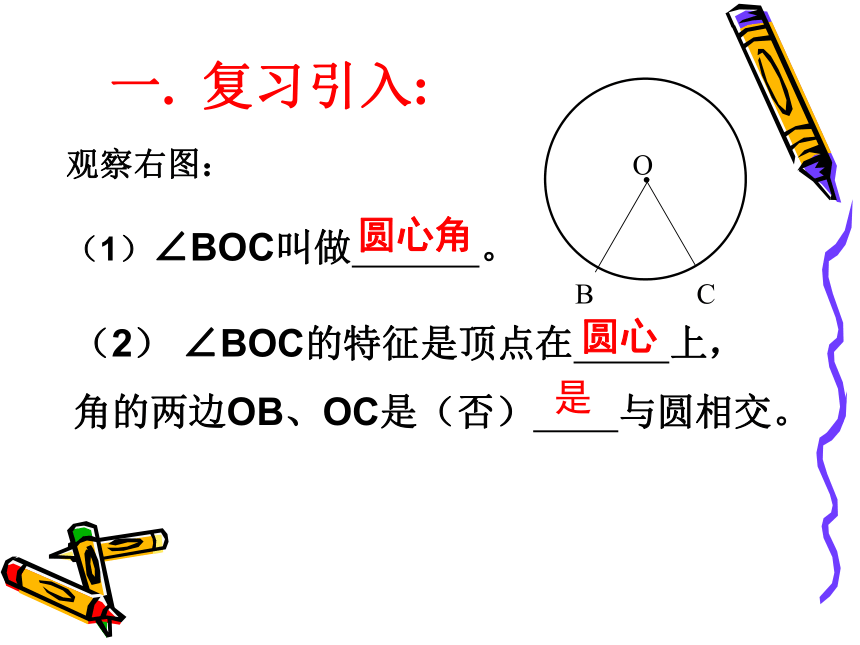
观察右图:
(1)∠BOC叫做
。
.
O
B
C
圆心角
(2)
∠BOC的特征是顶点在
上,
角的两边OB、OC是(否)
与圆相交。
圆心
是
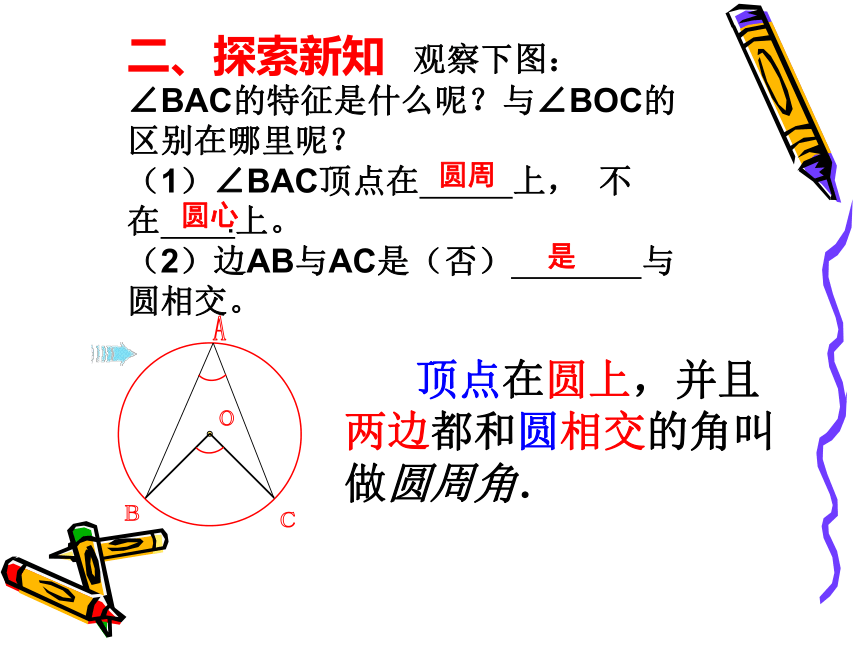
二、探索新知
观察下图:
∠BAC的特征是什么呢?与∠BOC的区别在哪里呢?
(1)∠BAC顶点在
上,
不在
.上。
(2)边AB与AC是(否)
与圆相交。
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
圆周
圆心
是
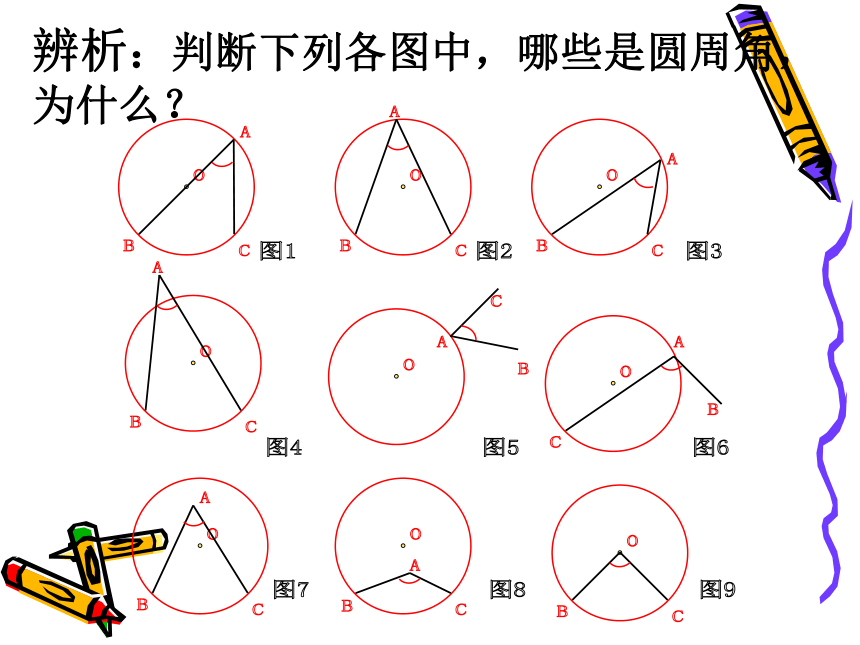
辨析:判断下列各图中,哪些是圆周角,为什么?
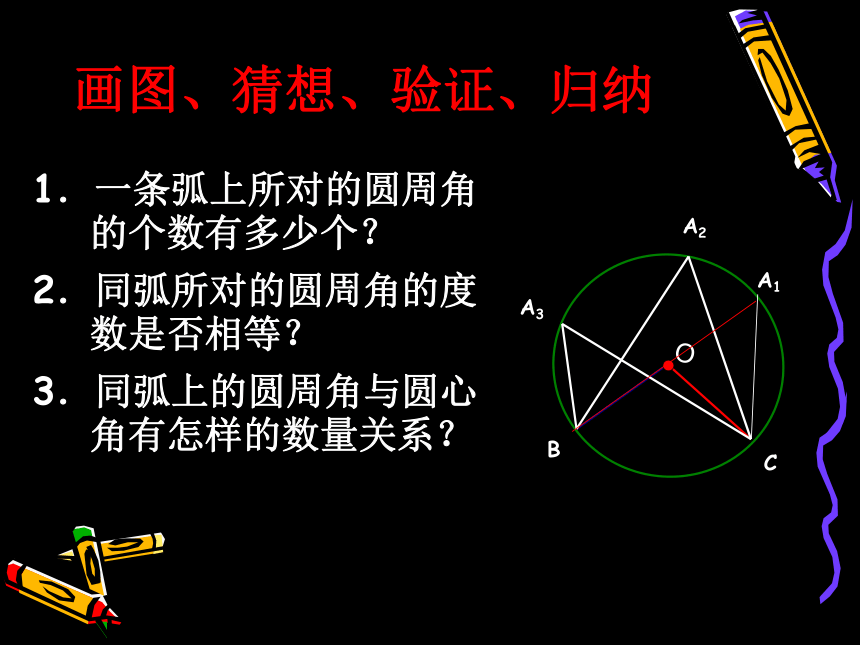
画图、猜想、验证、归纳
1.一条弧上所对的圆周角的个数有多少个?
2.同弧所对的圆周角的度数是否相等?
3.同弧上的圆周角与圆心角有怎样的数量关系?
B
O
A
D
C
E
A3
A2
A1
B
C
归纳:
1.一条弧所对的圆周角的个数有无数多个.
2.通过度量,我们可以发现,同弧所对的圆周角大小是没有变化的,都是相等的.
3.通过度量,我们可以得出,同弧上的圆周角都等于该弧所对圆心角的一半.
下面,我们通过逻辑证明来说明“同弧所对的圆周角的度数没有变化,都等于该弧所对的圆心角度数的一半.”
C
O
B
A3
A2
A1
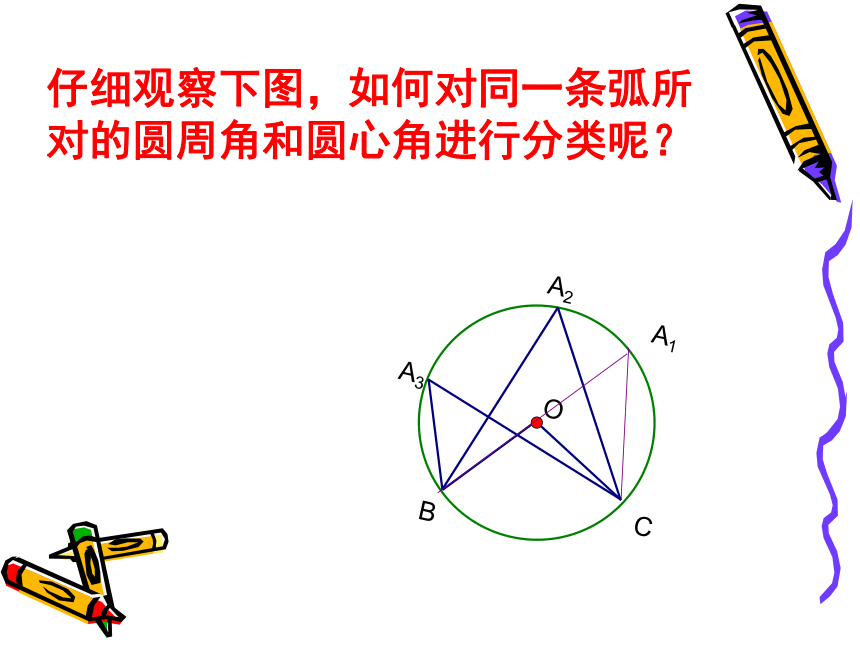
仔细观察下图,如何对同一条弧所对的圆周角和圆心角进行分类呢?
A
O
B
C
O
A
B
C
O
A
B
C
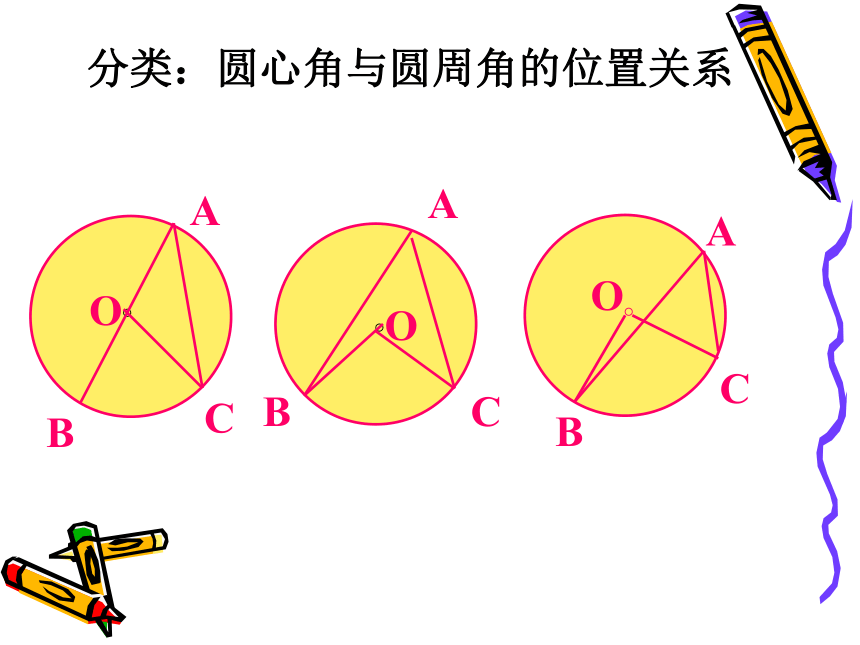
分类:圆心角与圆周角的位置关系
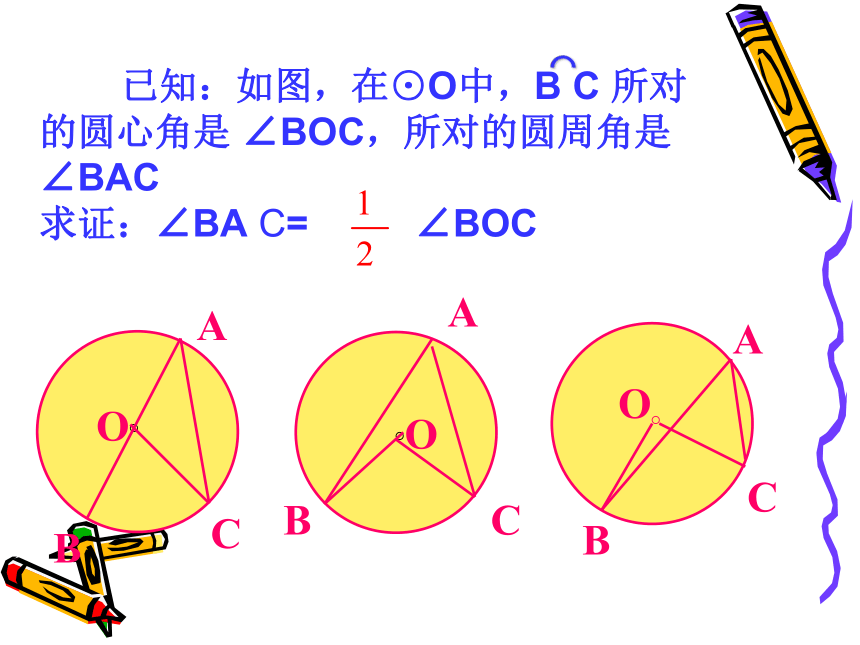
已知:如图,在⊙O中,B
C
所对的圆心角是
∠BOC,所对的圆周角是∠BAC
求证:∠BA
C=
∠BOC
⌒
A
O
B
C
O
A
B
C
O
A
B
C
分三种情况来证明:
(1)圆心在∠BAC的一边上。
A
O
B
C
∴
∠A=∠C
证明:∵OA=OC
又∵∠BOC=
∠A
+∠C
∴∠BOC=2
∠A
即∠A
=
∠BOC
一条弧所对的圆周角等于它所对的圆心角的一半.
(2)圆心在∠BAC的内部。
O
A
B
C
D
1
2
1
2
证明:作直径AD。
∵∠BAD=
∠BOD
∠DAC=
∠DOC
∴∠BAD+∠DAC=
(∠
BOD+∠DOC)
即:
∠BAC=
∠BOC
1
2
1
2
一条弧所对的圆周角等于它所对的圆心角的一半.
O
A
B
C
(3)圆心在∠BAC的外部。
D
证明:作直径AD。
∵∠DAB=
∠DOB
∠DAC=
∠DOC
∴
∠DAC-∠DAB=
(∠DOC-∠DOB)
即:
∠BAC=
∠BOC
1
2
1
2
1
2
1
2
一条弧所对的圆周角等于它所对的圆心角的一半.
综上所述,我们可以得到:
圆周角定理:
同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
C
O
B
A3
A2
A1
思考:
相等的圆周角所对的弧相等吗?
在同圆或等圆中,
1、判断:
(1)等弧所对的圆周角相等.
(
)
(2)相等的圆周角所对的弧也相等.(
)
(3)同弦所对的圆周角相等。
(
)
√
×
×
三、巩
固
练
习
(1)如果∠A=44°,则∠BOC=____.
(2)如果∠BOC=44°,则∠A=____.
(3)如果∠A=35°,则∠BDC=____.
O
A
B
C
D
2、计
算:
88°
22°
35°
3、如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
方法点拔:由同弧来找相等的圆周角
已知:AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°
。
求∠BOC的度数。
∠BOC
=140°
四、例
题
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。
2.圆周角性质:在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧也相等。
五、课
堂小
结
【中考链接】
1、(2013?徐州)如图,点A、B、C在⊙O上,若∠C=30°,则∠AOB的度数为
°.
60
2、(2013安顺)如图,A、B、C三点在⊙O上,且∠AOB=80°,则∠ACB的度数为
40
3、(2013鞍山)已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45°
B.35
C.25°
D.20°
A
4、(2013?淮安)如图,点A、B、C是⊙0上的三点,若∠OBC=50°,则∠A的度数是( )
A.40°B.50°C.80°D.100°
A
5、(2013泰安)如图,点A,B,C,
在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60°
B.70°
C.120°
D.140°
D
六、布置作业
必做作业
课本P122习题5.3第3、5题。
选做作业
补充习题P85第1---5题
一.
复习引入:
观察右图:
(1)∠BOC叫做
。
.
O
B
C
圆心角
(2)
∠BOC的特征是顶点在
上,
角的两边OB、OC是(否)
与圆相交。
圆心
是
二、探索新知
观察下图:
∠BAC的特征是什么呢?与∠BOC的区别在哪里呢?
(1)∠BAC顶点在
上,
不在
.上。
(2)边AB与AC是(否)
与圆相交。
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
圆周
圆心
是
辨析:判断下列各图中,哪些是圆周角,为什么?
画图、猜想、验证、归纳
1.一条弧上所对的圆周角的个数有多少个?
2.同弧所对的圆周角的度数是否相等?
3.同弧上的圆周角与圆心角有怎样的数量关系?
B
O
A
D
C
E
A3
A2
A1
B
C
归纳:
1.一条弧所对的圆周角的个数有无数多个.
2.通过度量,我们可以发现,同弧所对的圆周角大小是没有变化的,都是相等的.
3.通过度量,我们可以得出,同弧上的圆周角都等于该弧所对圆心角的一半.
下面,我们通过逻辑证明来说明“同弧所对的圆周角的度数没有变化,都等于该弧所对的圆心角度数的一半.”
C
O
B
A3
A2
A1
仔细观察下图,如何对同一条弧所对的圆周角和圆心角进行分类呢?
A
O
B
C
O
A
B
C
O
A
B
C
分类:圆心角与圆周角的位置关系
已知:如图,在⊙O中,B
C
所对的圆心角是
∠BOC,所对的圆周角是∠BAC
求证:∠BA
C=
∠BOC
⌒
A
O
B
C
O
A
B
C
O
A
B
C
分三种情况来证明:
(1)圆心在∠BAC的一边上。
A
O
B
C
∴
∠A=∠C
证明:∵OA=OC
又∵∠BOC=
∠A
+∠C
∴∠BOC=2
∠A
即∠A
=
∠BOC
一条弧所对的圆周角等于它所对的圆心角的一半.
(2)圆心在∠BAC的内部。
O
A
B
C
D
1
2
1
2
证明:作直径AD。
∵∠BAD=
∠BOD
∠DAC=
∠DOC
∴∠BAD+∠DAC=
(∠
BOD+∠DOC)
即:
∠BAC=
∠BOC
1
2
1
2
一条弧所对的圆周角等于它所对的圆心角的一半.
O
A
B
C
(3)圆心在∠BAC的外部。
D
证明:作直径AD。
∵∠DAB=
∠DOB
∠DAC=
∠DOC
∴
∠DAC-∠DAB=
(∠DOC-∠DOB)
即:
∠BAC=
∠BOC
1
2
1
2
1
2
1
2
一条弧所对的圆周角等于它所对的圆心角的一半.
综上所述,我们可以得到:
圆周角定理:
同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
C
O
B
A3
A2
A1
思考:
相等的圆周角所对的弧相等吗?
在同圆或等圆中,
1、判断:
(1)等弧所对的圆周角相等.
(
)
(2)相等的圆周角所对的弧也相等.(
)
(3)同弦所对的圆周角相等。
(
)
√
×
×
三、巩
固
练
习
(1)如果∠A=44°,则∠BOC=____.
(2)如果∠BOC=44°,则∠A=____.
(3)如果∠A=35°,则∠BDC=____.
O
A
B
C
D
2、计
算:
88°
22°
35°
3、如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
方法点拔:由同弧来找相等的圆周角
已知:AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°
。
求∠BOC的度数。
∠BOC
=140°
四、例
题
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角。
2.圆周角性质:在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧也相等。
五、课
堂小
结
【中考链接】
1、(2013?徐州)如图,点A、B、C在⊙O上,若∠C=30°,则∠AOB的度数为
°.
60
2、(2013安顺)如图,A、B、C三点在⊙O上,且∠AOB=80°,则∠ACB的度数为
40
3、(2013鞍山)已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45°
B.35
C.25°
D.20°
A
4、(2013?淮安)如图,点A、B、C是⊙0上的三点,若∠OBC=50°,则∠A的度数是( )
A.40°B.50°C.80°D.100°
A
5、(2013泰安)如图,点A,B,C,
在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60°
B.70°
C.120°
D.140°
D
六、布置作业
必做作业
课本P122习题5.3第3、5题。
选做作业
补充习题P85第1---5题
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
