苏科版数学九年级上册 2.4圆周角课件(共21张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 2.4圆周角课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 652.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 00:00:00 | ||
图片预览


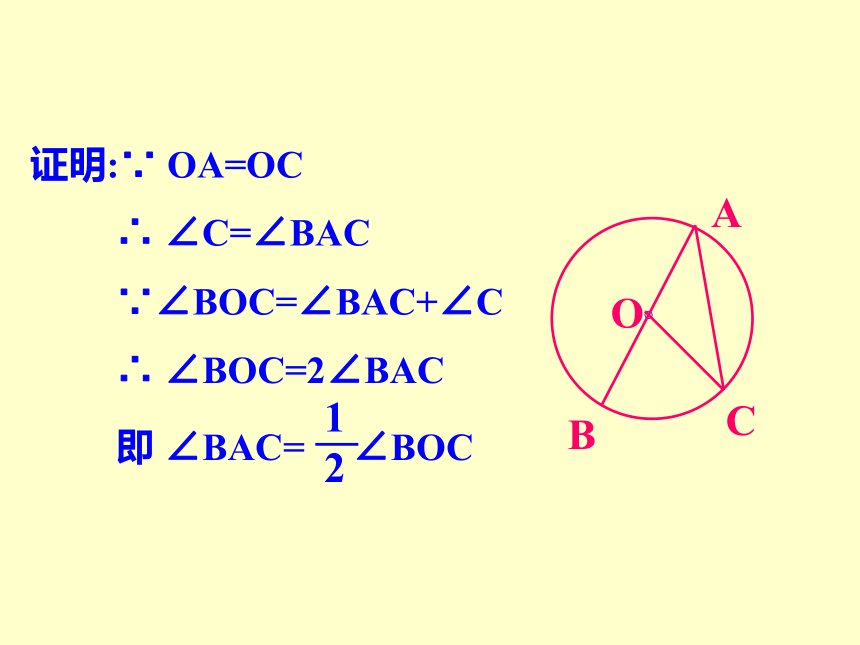
文档简介
(共21张PPT)
学习目标
1. 知道圆周角的定义,理解圆周角、圆心角、弧的度数之间的区别联系。
2. 通过对圆周角定理的证明,培养自己解决数学问题中的分类的数学 思想和方法。
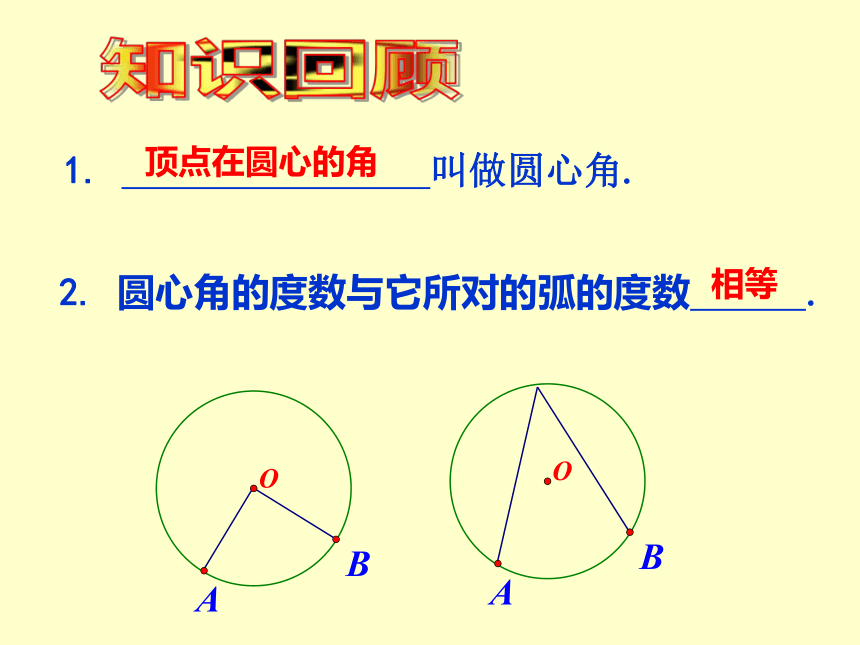
1. 叫做圆心角.
顶点在圆心的角
2. 圆心角的度数与它所对的弧的度数 .
相等
O
A
B
O
A
B
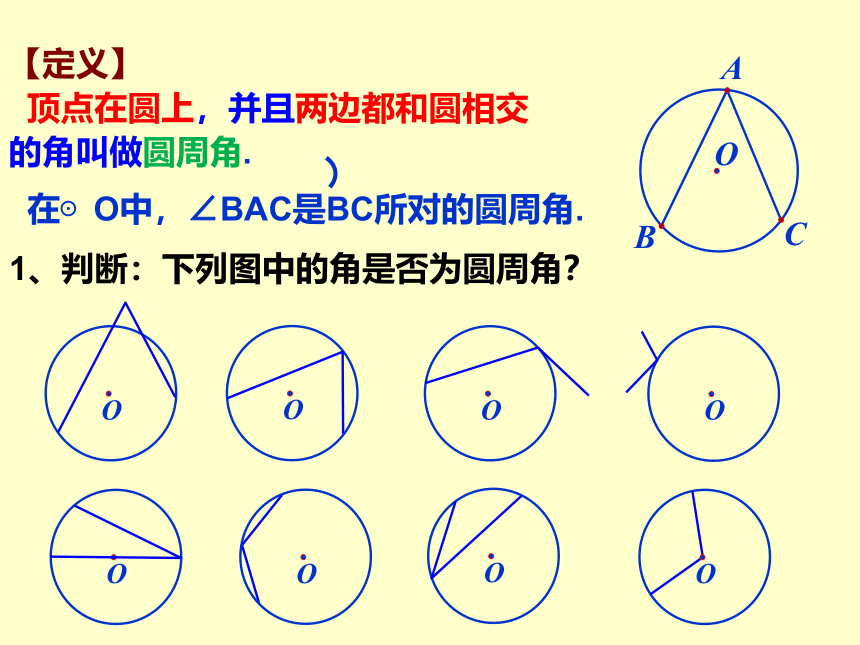
【定义】
顶点在圆上,并且两边都和圆相交
的角叫做圆周角.
C
B
O
A
1、判断:下列图中的角是否为圆周角?
O
O
O
O
O
O
O
O
在⊙O中,∠BAC是BC所对的圆周角.
(
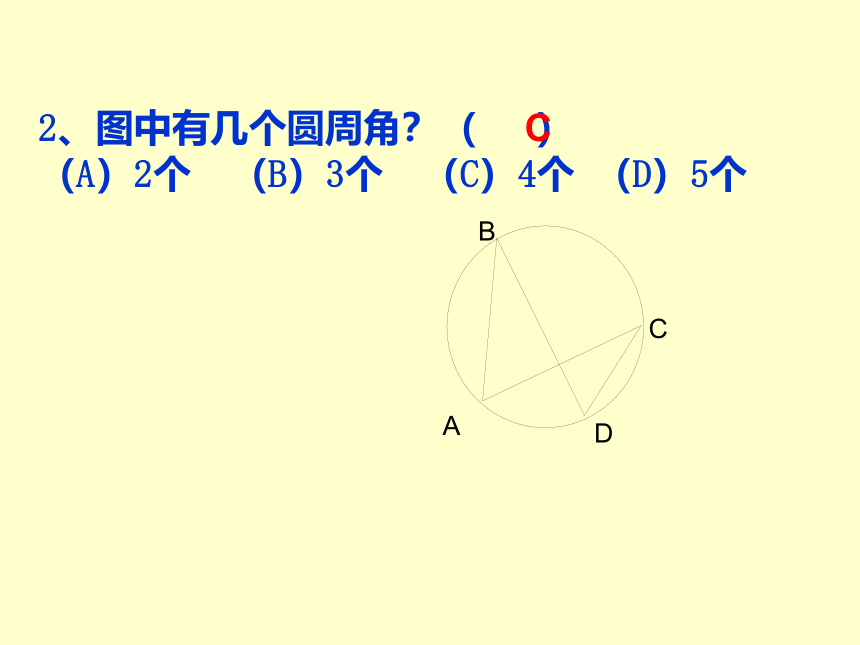
2、图中有几个圆周角?( )
(A)2个 (B)3个 (C)4个 (D)5个
C
O
A2
A3
C
B
A1
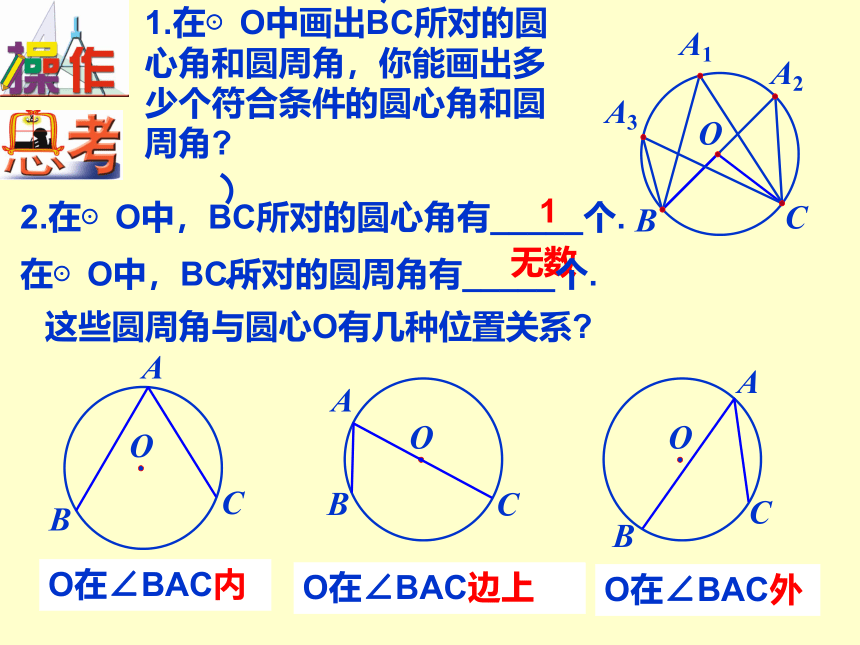
1.在⊙O中画出BC所对的圆
心角和圆周角,你能画出多
少个符合条件的圆心角和圆
周角
(
2.在⊙O中,BC所对的圆心角有_____个.
(
O在∠BAC内
O在∠BAC边上
O在∠BAC外
O
B
C
A
O
A
C
B
O
B
A
C
无数
这些圆周角与圆心O有几种位置关系
在⊙O中,BC所对的圆周角有_____个.
(
1
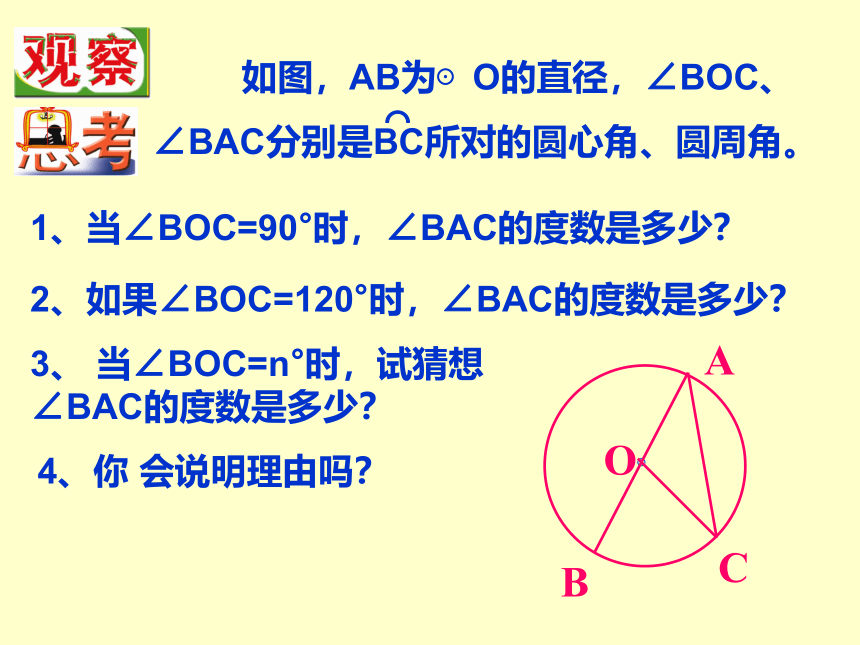
如图,AB为⊙O的直径,∠BOC、
∠BAC分别是BC所对的圆心角、圆周角。
⌒
1、当∠BOC=90°时,∠BAC的度数是多少?
2、如果∠BOC=120°时,∠BAC的度数是多少?
3、 当∠BOC=n°时,试猜想∠BAC的度数是多少?
4、你 会说明理由吗?
A
O
B
C
A
O
B
C
证明:∵ OA=OC
∴ ∠C=∠BAC
∵∠BOC=∠BAC+∠C
∴ ∠BOC=2∠BAC
1
2
即 ∠BAC= ∠BOC
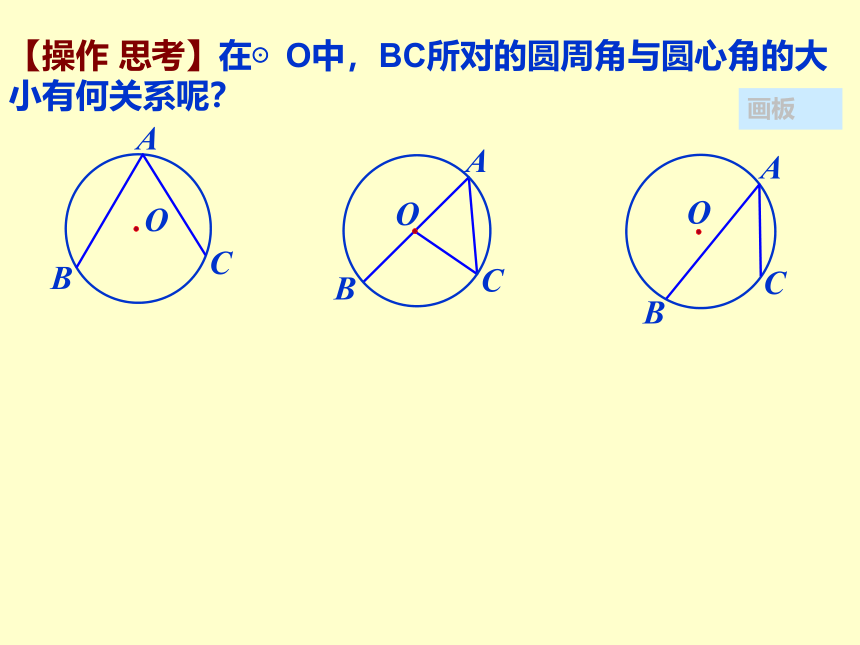
【操作 思考】在⊙O中,BC所对的圆周角与圆心角的大小有何关系呢?
O
B
C
A
O
A
C
B
O
B
A
C
画板
我们根据圆周角相对于圆心的位置把圆周角分成三类,先解决一类特殊问题,再把其他两类转化成特殊问题。
定理的证明思路:
圆心在∠BAC的内部.
O
A
B
C
D
1
2
1
2
证明:作直径AD.
∵∠BAD= ∠BOD
∠DAC= ∠DOC
∵∠BAD+∠DAC= (∠ BOD+∠DOC)
即: ∠BAC= ∠BOC
1
2
1
2
,
证明:作直径AD.
即
.
∵
,
.
∴
圆心在∠BAC的外部.
【操作 思考】在⊙O中,BC所对的圆周角与圆心角的大小有何关系呢?
O
B
C
A
O
A
C
B
O
B
A
C
画板
【圆周角定理】
圆周角的度数等于它所对弧上的圆心角度数的一半,
圆周角的度数等于它所对弧的度数的一半.
同弧或等弧所对的圆周角相等.
O
B
C
A
D
1、 如图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线的同侧,∠BAC=35°。
(1) ∠BDC=____ °,
理由是____________________;
(2) ∠BOC=____ °,
理由是_____________________;
35
同弧所对的圆周角相等
70
同弧所对的圆周等于该弧所对的圆心角的一半
2、如图6,已知∠ACB = 20 ,则∠AOB = _____, ∠OAB = .
40
70
3、如图7,已知圆心角∠AOB=1000,则∠ACB = _______。
A
O
B
变式:
如图,在⊙O中,∠AOB=50°,点C在圆上运动(不与A、B重合),则∠ACB = _______。
130
25 或155
O
A
B
E
C
D
【例1】如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°,BC为70°,求∠ABD、∠AED的度数.
(
【例2】如图,点A、B、C、D在⊙O上,
∠ABC=∠ADB=60°,BC=3.
求△ABC的周长.
D
C
O
A B
【例3】如图,△ABC的3个顶点都在⊙O上,D是弧AC的中点,BD交AC于点E,△CDE与△BDC相似吗?为什么?
(1)顶点在圆上,并且两边都和圆相交的角叫做圆周角.
(2)同弧所对的圆心角只有一个,所对的圆周 角有无数个.
(3)圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等.
(4)圆周角的度数等于它所对弧的度数的一半.
如图,点A、B、C在⊙O上,点D在圆外,
CD、BD分别交⊙O于点E、F,比较∠BAC
与∠BDC的大小,并说明理由。
解:连接CF,
∵ ∠BFC是△BFC的一个外角
∴ ∠BFC > ∠BDC
∵ ∠BAC = ∠BFC (同弧所对的圆周角相等)
∴ ∠BAC > ∠BDC
学习目标
1. 知道圆周角的定义,理解圆周角、圆心角、弧的度数之间的区别联系。
2. 通过对圆周角定理的证明,培养自己解决数学问题中的分类的数学 思想和方法。
1. 叫做圆心角.
顶点在圆心的角
2. 圆心角的度数与它所对的弧的度数 .
相等
O
A
B
O
A
B
【定义】
顶点在圆上,并且两边都和圆相交
的角叫做圆周角.
C
B
O
A
1、判断:下列图中的角是否为圆周角?
O
O
O
O
O
O
O
O
在⊙O中,∠BAC是BC所对的圆周角.
(
2、图中有几个圆周角?( )
(A)2个 (B)3个 (C)4个 (D)5个
C
O
A2
A3
C
B
A1
1.在⊙O中画出BC所对的圆
心角和圆周角,你能画出多
少个符合条件的圆心角和圆
周角
(
2.在⊙O中,BC所对的圆心角有_____个.
(
O在∠BAC内
O在∠BAC边上
O在∠BAC外
O
B
C
A
O
A
C
B
O
B
A
C
无数
这些圆周角与圆心O有几种位置关系
在⊙O中,BC所对的圆周角有_____个.
(
1
如图,AB为⊙O的直径,∠BOC、
∠BAC分别是BC所对的圆心角、圆周角。
⌒
1、当∠BOC=90°时,∠BAC的度数是多少?
2、如果∠BOC=120°时,∠BAC的度数是多少?
3、 当∠BOC=n°时,试猜想∠BAC的度数是多少?
4、你 会说明理由吗?
A
O
B
C
A
O
B
C
证明:∵ OA=OC
∴ ∠C=∠BAC
∵∠BOC=∠BAC+∠C
∴ ∠BOC=2∠BAC
1
2
即 ∠BAC= ∠BOC
【操作 思考】在⊙O中,BC所对的圆周角与圆心角的大小有何关系呢?
O
B
C
A
O
A
C
B
O
B
A
C
画板
我们根据圆周角相对于圆心的位置把圆周角分成三类,先解决一类特殊问题,再把其他两类转化成特殊问题。
定理的证明思路:
圆心在∠BAC的内部.
O
A
B
C
D
1
2
1
2
证明:作直径AD.
∵∠BAD= ∠BOD
∠DAC= ∠DOC
∵∠BAD+∠DAC= (∠ BOD+∠DOC)
即: ∠BAC= ∠BOC
1
2
1
2
,
证明:作直径AD.
即
.
∵
,
.
∴
圆心在∠BAC的外部.
【操作 思考】在⊙O中,BC所对的圆周角与圆心角的大小有何关系呢?
O
B
C
A
O
A
C
B
O
B
A
C
画板
【圆周角定理】
圆周角的度数等于它所对弧上的圆心角度数的一半,
圆周角的度数等于它所对弧的度数的一半.
同弧或等弧所对的圆周角相等.
O
B
C
A
D
1、 如图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线的同侧,∠BAC=35°。
(1) ∠BDC=____ °,
理由是____________________;
(2) ∠BOC=____ °,
理由是_____________________;
35
同弧所对的圆周角相等
70
同弧所对的圆周等于该弧所对的圆心角的一半
2、如图6,已知∠ACB = 20 ,则∠AOB = _____, ∠OAB = .
40
70
3、如图7,已知圆心角∠AOB=1000,则∠ACB = _______。
A
O
B
变式:
如图,在⊙O中,∠AOB=50°,点C在圆上运动(不与A、B重合),则∠ACB = _______。
130
25 或155
O
A
B
E
C
D
【例1】如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°,BC为70°,求∠ABD、∠AED的度数.
(
【例2】如图,点A、B、C、D在⊙O上,
∠ABC=∠ADB=60°,BC=3.
求△ABC的周长.
D
C
O
A B
【例3】如图,△ABC的3个顶点都在⊙O上,D是弧AC的中点,BD交AC于点E,△CDE与△BDC相似吗?为什么?
(1)顶点在圆上,并且两边都和圆相交的角叫做圆周角.
(2)同弧所对的圆心角只有一个,所对的圆周 角有无数个.
(3)圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等.
(4)圆周角的度数等于它所对弧的度数的一半.
如图,点A、B、C在⊙O上,点D在圆外,
CD、BD分别交⊙O于点E、F,比较∠BAC
与∠BDC的大小,并说明理由。
解:连接CF,
∵ ∠BFC是△BFC的一个外角
∴ ∠BFC > ∠BDC
∵ ∠BAC = ∠BFC (同弧所对的圆周角相等)
∴ ∠BAC > ∠BDC
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
