苏科版数学九年级上册 2.5直线与圆的位置关系 课件(共23张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 2.5直线与圆的位置关系 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 23:50:27 | ||
图片预览








文档简介
(共23张PPT)
2.5 直线与圆的位置关系(1)
九年级(上册)
初中数学
第二章
对称图形—圆
2.5
直线与圆的位置关系(1)
请你想一想
1.我们已经学习过点和圆的位置关系,请同学们回忆:
(1)点和圆有哪几种位置关系?
(2)怎样判定点和圆的位置关系?(数量关系——位置关系)
2.5
直线与圆的位置关系(1)
请你看一看
2.观察三幅太阳升起的照片,地平线与太阳经历了哪些位置关系?
通过这个自然现象,你猜想直线和圆的位置关系有哪几种?
通过这个自然现象,你猜想直线和圆的位置关系有哪几种?
2.5
直线与圆的位置关系(1)
请你看一看
2.5
直线与圆的位置关系(1)
请你画一画
(1)直线和圆有两个公共点.
2.5
直线与圆的位置关系(1)
请你画一画
(2)直线和圆有一个公共点.
2.5
直线与圆的位置关系(1)
请你画一画
(3)直线和圆没有公共点.
2.5
直线与圆的位置关系(1)
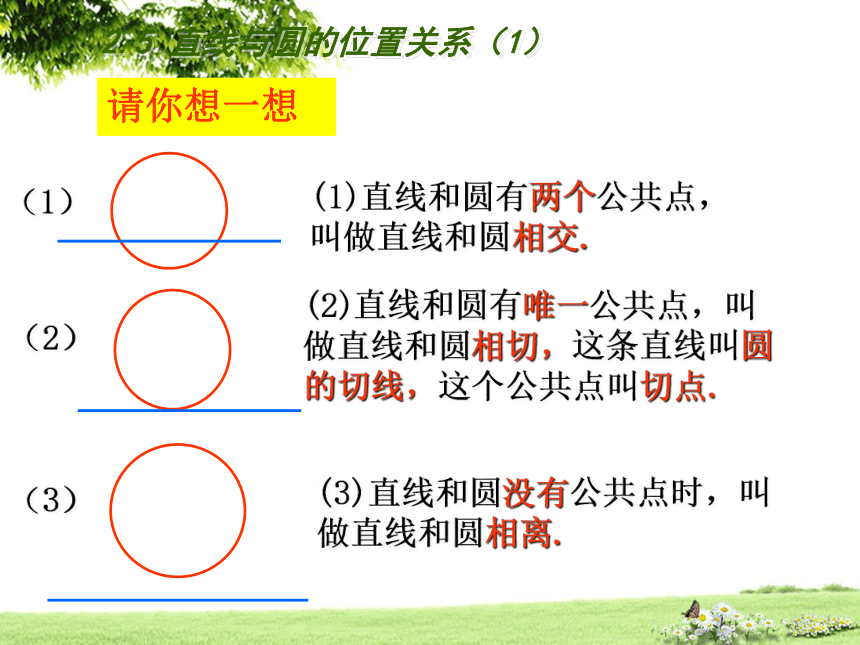
(2)直线和圆有唯一公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(1)直线和圆有两个公共点,叫做直线和圆相交.
(3)直线和圆没有公共点时,叫做直线和圆相离.
(1)
(2)
(3)
请你想一想
2.5
直线与圆的位置关系(1)
请你想一想
前面复习知道:
点和圆的位置关系可以用圆心到点之间的距离,这一数量关系来刻画它们的位置关系;
那么直线和圆的位置关系是否也可以用数量关系来刻画它们的三种位置关系呢?
2.5
直线与圆的位置关系(1)
请你想一想
3.直线与圆相离
<=>
d>r
2.直线与圆相切
<=>
d=r
1.直线与圆相交
<=>
d<r
当直线与圆相交、相切、相离时,d与r有何关系?
(3)相离
d
.O
r
d
O
(2)相切
r
d
O
(1)相交
r
2.5
直线与圆的位置关系(1)
请你想一想
点与圆有3种不同的位置关系,直线与圆也有3种不同的位置关系,这两者之间有怎样的联系?
直线与圆的3种位置关系,实质上就是
点(垂足)与圆的3种位置关系。
2.5
直线与圆的位置关系(1)
典型例题
例1 在△ABC中,∠A=45°,AC=4,以C为圆心,r为半径的圆与AB所在直线有怎样的位置关系?为什么?
(1)r=2;(2)r=2 ;(3)r=3.
A
B
C
如图,在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)
r=2
(2)
r=2
(3)
r=3
450
4
D
2
450
4
D
2
450
4
D
2
·
·
相离
相切
相交
例题分析
1.判断正误
1)与圆有公共点的直线是圆的切线
(
)
2)过圆外一点画一条直线,则直线与圆相离(
)
3)过圆内一点画一条直线,则直线与圆相交(
)
×
×
√
2.
设⊙O的半径为3,直线a上一点到圆心的距离为3,则直线a与⊙O的位置关系是(
)
(A)相交
(B)相切
(C)相离
(D)相切或相交
D
当堂检测:
2.5
直线与圆的位置关系(1)
3.已知⊙O的直径为8,圆心O到直线l的距离为5,直线l与⊙O有怎样的位置关系?圆心O到直线l的距离为4或3呢?
当堂检测:
2.5
直线与圆的位置关系(1)
课堂练习
4.在Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的圆与AB所在直线有怎样的位置关系?为什么?
(1)r=2;(2)r=2.4;(3)r=3.
2.5
直线与圆的位置关系(1)
请你说一说
1.这节课你有哪些收获和困惑?
2.直线与圆的位置关系中的d与点和圆的位置关系中的d,两者有何区别与联系?
2.5
直线与圆的位置关系(1)
0
d>r
1
d=r
切点
切线
2
d<r
O
d
┐
┐
r
d
相离
相切
相交
O
┐
r
C
B
r
A
.o
d
P
2.5
直线与圆的位置关系(1)
课堂总结
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)根据性质,由___________________________
的关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
2.5
直线与圆的位置关系(1)
1.已知:如图示,∠AOB=30°,M为OB上
一点,以M为圆心,5cm长为半径作圆,若M在OB上
运动,问:
①当OM满足
时,⊙M与OA相离?
②当OM满足
时,⊙M与OA相切?
③当OM满足
时,⊙M与OA相交?
A
B
O
M
.
拓展提升
2.5
直线与圆的位置关系(1)
拓展提升
2.在平面直角坐标系中有一点A(-3,-4),以点A为圆心,r长为半径时,思考:随着r的变化,⊙A与坐标轴交点的变化情况.
.
A
y
x
2.5
直线与圆的位置关系(1)
课后作业
课本P73
2.5习题第1、2题.
谢
谢!
2.5 直线与圆的位置关系(1)
九年级(上册)
初中数学
第二章
对称图形—圆
2.5
直线与圆的位置关系(1)
请你想一想
1.我们已经学习过点和圆的位置关系,请同学们回忆:
(1)点和圆有哪几种位置关系?
(2)怎样判定点和圆的位置关系?(数量关系——位置关系)
2.5
直线与圆的位置关系(1)
请你看一看
2.观察三幅太阳升起的照片,地平线与太阳经历了哪些位置关系?
通过这个自然现象,你猜想直线和圆的位置关系有哪几种?
通过这个自然现象,你猜想直线和圆的位置关系有哪几种?
2.5
直线与圆的位置关系(1)
请你看一看
2.5
直线与圆的位置关系(1)
请你画一画
(1)直线和圆有两个公共点.
2.5
直线与圆的位置关系(1)
请你画一画
(2)直线和圆有一个公共点.
2.5
直线与圆的位置关系(1)
请你画一画
(3)直线和圆没有公共点.
2.5
直线与圆的位置关系(1)
(2)直线和圆有唯一公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(1)直线和圆有两个公共点,叫做直线和圆相交.
(3)直线和圆没有公共点时,叫做直线和圆相离.
(1)
(2)
(3)
请你想一想
2.5
直线与圆的位置关系(1)
请你想一想
前面复习知道:
点和圆的位置关系可以用圆心到点之间的距离,这一数量关系来刻画它们的位置关系;
那么直线和圆的位置关系是否也可以用数量关系来刻画它们的三种位置关系呢?
2.5
直线与圆的位置关系(1)
请你想一想
3.直线与圆相离
<=>
d>r
2.直线与圆相切
<=>
d=r
1.直线与圆相交
<=>
d<r
当直线与圆相交、相切、相离时,d与r有何关系?
(3)相离
d
.O
r
d
O
(2)相切
r
d
O
(1)相交
r
2.5
直线与圆的位置关系(1)
请你想一想
点与圆有3种不同的位置关系,直线与圆也有3种不同的位置关系,这两者之间有怎样的联系?
直线与圆的3种位置关系,实质上就是
点(垂足)与圆的3种位置关系。
2.5
直线与圆的位置关系(1)
典型例题
例1 在△ABC中,∠A=45°,AC=4,以C为圆心,r为半径的圆与AB所在直线有怎样的位置关系?为什么?
(1)r=2;(2)r=2 ;(3)r=3.
A
B
C
如图,在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)
r=2
(2)
r=2
(3)
r=3
450
4
D
2
450
4
D
2
450
4
D
2
·
·
相离
相切
相交
例题分析
1.判断正误
1)与圆有公共点的直线是圆的切线
(
)
2)过圆外一点画一条直线,则直线与圆相离(
)
3)过圆内一点画一条直线,则直线与圆相交(
)
×
×
√
2.
设⊙O的半径为3,直线a上一点到圆心的距离为3,则直线a与⊙O的位置关系是(
)
(A)相交
(B)相切
(C)相离
(D)相切或相交
D
当堂检测:
2.5
直线与圆的位置关系(1)
3.已知⊙O的直径为8,圆心O到直线l的距离为5,直线l与⊙O有怎样的位置关系?圆心O到直线l的距离为4或3呢?
当堂检测:
2.5
直线与圆的位置关系(1)
课堂练习
4.在Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的圆与AB所在直线有怎样的位置关系?为什么?
(1)r=2;(2)r=2.4;(3)r=3.
2.5
直线与圆的位置关系(1)
请你说一说
1.这节课你有哪些收获和困惑?
2.直线与圆的位置关系中的d与点和圆的位置关系中的d,两者有何区别与联系?
2.5
直线与圆的位置关系(1)
0
d>r
1
d=r
切点
切线
2
d<r
O
d
┐
┐
r
d
相离
相切
相交
O
┐
r
C
B
r
A
.o
d
P
2.5
直线与圆的位置关系(1)
课堂总结
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由________________的个数来判断;
(2)根据性质,由___________________________
的关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
2.5
直线与圆的位置关系(1)
1.已知:如图示,∠AOB=30°,M为OB上
一点,以M为圆心,5cm长为半径作圆,若M在OB上
运动,问:
①当OM满足
时,⊙M与OA相离?
②当OM满足
时,⊙M与OA相切?
③当OM满足
时,⊙M与OA相交?
A
B
O
M
.
拓展提升
2.5
直线与圆的位置关系(1)
拓展提升
2.在平面直角坐标系中有一点A(-3,-4),以点A为圆心,r长为半径时,思考:随着r的变化,⊙A与坐标轴交点的变化情况.
.
A
y
x
2.5
直线与圆的位置关系(1)
课后作业
课本P73
2.5习题第1、2题.
谢
谢!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
