苏科版数学九年级上册 2.5直线与圆的位置关系(2)课件(17张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 2.5直线与圆的位置关系(2)课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 05:57:12 | ||
图片预览






文档简介
(共17张PPT)
2.5 直线与圆的位置关系(2)
九年级(上册)
初中数学
温故知新
1.已知圆的半径等于5厘米,圆心到直线l的距离分别是:(1)4厘米;(2)5厘米;(3)6厘米.直线l与圆的位置关系是怎样的?
2.圆的切线的判定方法:
温故知新
(1)和圆有唯一公共点的直线是圆的切线;
(2)到圆心的距离等于这个圆的半径的直线(即d=r)是圆的切线.
操作与思考:
1.经过圆上一点A画一条圆的切线,并说明画图的依据.
A
O
归纳:
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
判定定理的2个条件:
①经过半径的外端;
②垂直于这条半径.
判断题:
1.经过半径外端的直线是圆的切线.(
)
2.经过半径的一端并且垂直于这条半径的直线是圆的切线.(
)
3.经过半径的外端并且垂直于这条半径的直线是圆的切线.(
)
4.到圆心的距离等于这个圆的半径的直线是圆的切线.(
)
5.经过直径的一端并且垂直于这条直径的直线是圆的切线.(
)
√
√
√
×
×
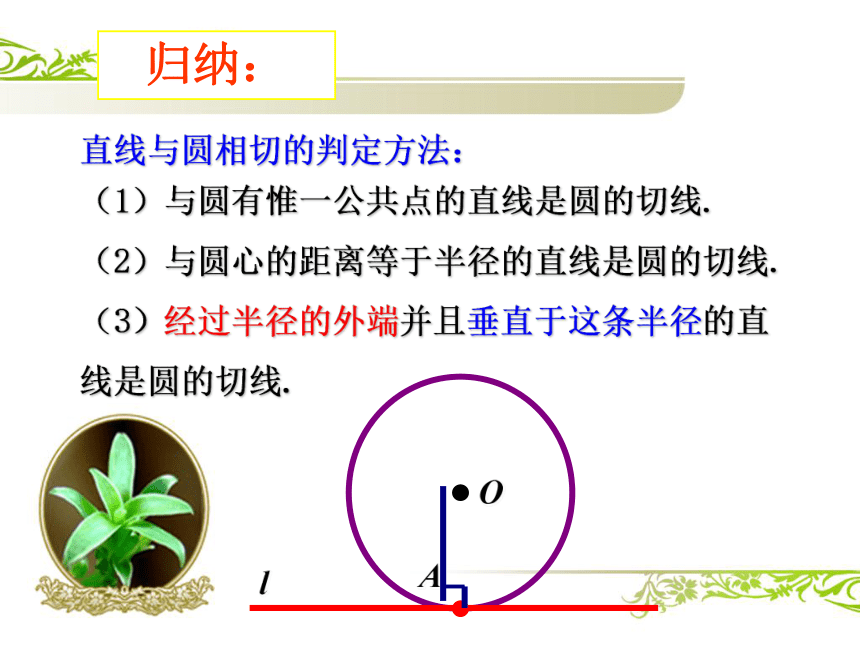
归纳:
A
O
l
(1)与圆有惟一公共点的直线是圆的切线.
(2)与圆心的距离等于半径的直线是圆的切线.
(3)经过半径的外端并且垂直于这条半径的直线是圆的切线.
直线与圆相切的判定方法:
例1.△ABC内接于⊙O,AB是⊙O的直径,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
典型例题
A
B
C
D
O
变式:
如图,△ABC内接于⊙O,AB是⊙O的弦,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
证明切线的方法:
当直线与圆有交点时,连半径,证垂直.
O
A
B
C
D
E
探究:
A
O
l
圆的切线垂直于经过切点的半径.
切线的性质:
反证法:
(1)假设直线l与OA不垂直.
(2)作OB⊥
l,垂足为点B.
(4)所以,直线l与圆相交,与“直线l与圆相切”矛盾.
(3)因为OB<OA,即d
<
r.
B
直线l与⊙O相切于点A,那么半径
吗?
切线的性质定理:
圆的切线垂直于过切点的半径.
∵CD是⊙O的切线,A是切点,
∴CD⊥OA.
C
D
●O
A
已知直线和圆相切时,经常作出
经过切点的半径.
归
纳
典例赏析:
例2 如图,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,DE与AC有怎样的位置关系?为什么?
当堂检测:
1.如图,O是∠ABC的平分线上的一点,OD⊥BC于D,以O为圆心、OD为半径的圆与AB相切吗?为什么?
2.如图,AB是⊙O的直径,∠ABC=45°,
AB=AC.判断直线AC与⊙O的位置关系,并说明
理由.
3.如图:在△ABC中AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.
求证:直线DE是⊙O的切线.
反思提升:
1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.切线的性质定理:圆的切线垂直于经过切点的半径.
2.切线的判定方法:
当已知直线过圆上的某一点时,要证明这条直线是圆的切线,作半径,证垂直.
(2)当已知直线与圆的公共点不明确时,
作垂直,证半径.
2.5 直线与圆的位置关系(2)
九年级(上册)
初中数学
温故知新
1.已知圆的半径等于5厘米,圆心到直线l的距离分别是:(1)4厘米;(2)5厘米;(3)6厘米.直线l与圆的位置关系是怎样的?
2.圆的切线的判定方法:
温故知新
(1)和圆有唯一公共点的直线是圆的切线;
(2)到圆心的距离等于这个圆的半径的直线(即d=r)是圆的切线.
操作与思考:
1.经过圆上一点A画一条圆的切线,并说明画图的依据.
A
O
归纳:
切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
判定定理的2个条件:
①经过半径的外端;
②垂直于这条半径.
判断题:
1.经过半径外端的直线是圆的切线.(
)
2.经过半径的一端并且垂直于这条半径的直线是圆的切线.(
)
3.经过半径的外端并且垂直于这条半径的直线是圆的切线.(
)
4.到圆心的距离等于这个圆的半径的直线是圆的切线.(
)
5.经过直径的一端并且垂直于这条直径的直线是圆的切线.(
)
√
√
√
×
×
归纳:
A
O
l
(1)与圆有惟一公共点的直线是圆的切线.
(2)与圆心的距离等于半径的直线是圆的切线.
(3)经过半径的外端并且垂直于这条半径的直线是圆的切线.
直线与圆相切的判定方法:
例1.△ABC内接于⊙O,AB是⊙O的直径,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
典型例题
A
B
C
D
O
变式:
如图,△ABC内接于⊙O,AB是⊙O的弦,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
证明切线的方法:
当直线与圆有交点时,连半径,证垂直.
O
A
B
C
D
E
探究:
A
O
l
圆的切线垂直于经过切点的半径.
切线的性质:
反证法:
(1)假设直线l与OA不垂直.
(2)作OB⊥
l,垂足为点B.
(4)所以,直线l与圆相交,与“直线l与圆相切”矛盾.
(3)因为OB<OA,即d
<
r.
B
直线l与⊙O相切于点A,那么半径
吗?
切线的性质定理:
圆的切线垂直于过切点的半径.
∵CD是⊙O的切线,A是切点,
∴CD⊥OA.
C
D
●O
A
已知直线和圆相切时,经常作出
经过切点的半径.
归
纳
典例赏析:
例2 如图,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,DE与AC有怎样的位置关系?为什么?
当堂检测:
1.如图,O是∠ABC的平分线上的一点,OD⊥BC于D,以O为圆心、OD为半径的圆与AB相切吗?为什么?
2.如图,AB是⊙O的直径,∠ABC=45°,
AB=AC.判断直线AC与⊙O的位置关系,并说明
理由.
3.如图:在△ABC中AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.
求证:直线DE是⊙O的切线.
反思提升:
1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.切线的性质定理:圆的切线垂直于经过切点的半径.
2.切线的判定方法:
当已知直线过圆上的某一点时,要证明这条直线是圆的切线,作半径,证垂直.
(2)当已知直线与圆的公共点不明确时,
作垂直,证半径.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
