七年级数学镶嵌
图片预览




文档简介
(共26张PPT)
课题学习——镶嵌
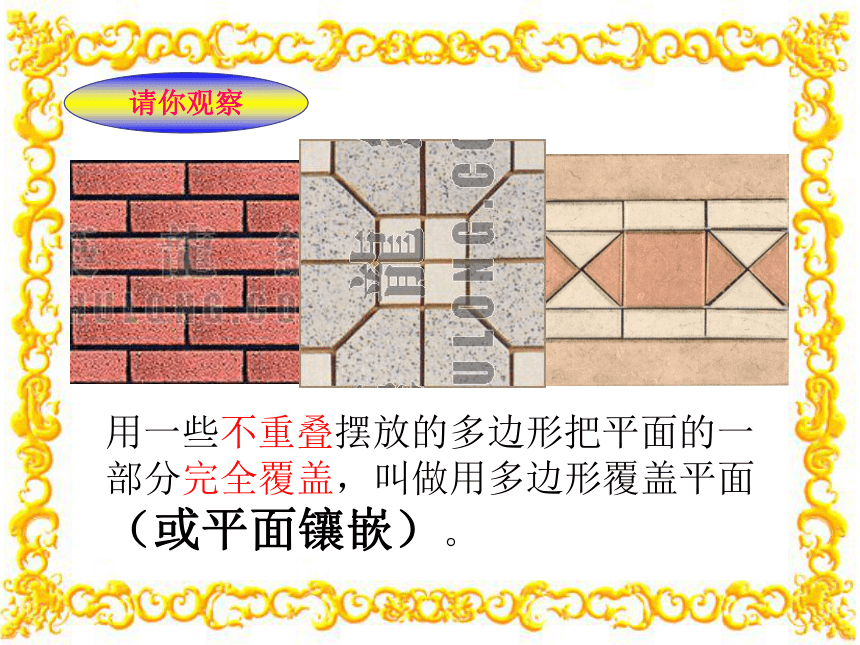
用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面(或平面镶嵌)。
请你观察
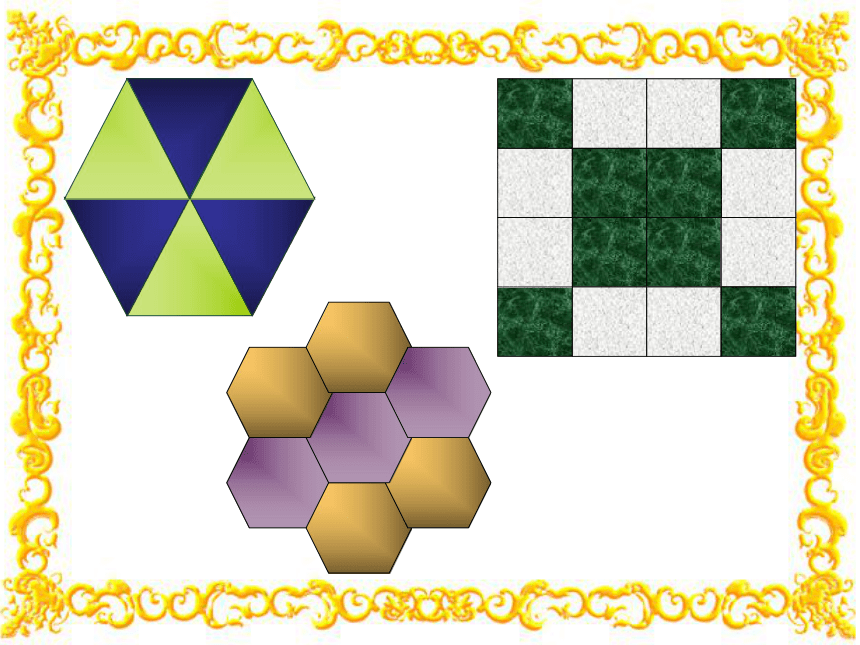
你能只用一种正多边形(如正三角形,正四边形,正六边形)拼成一个地面吗?(用自制的正三角形,正方形,正六边形纸片进行实验)
问题1:如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
仅用正多边形进行镶嵌,要嵌成一个平面,必须要求在公共顶点上所有内角和为360 。
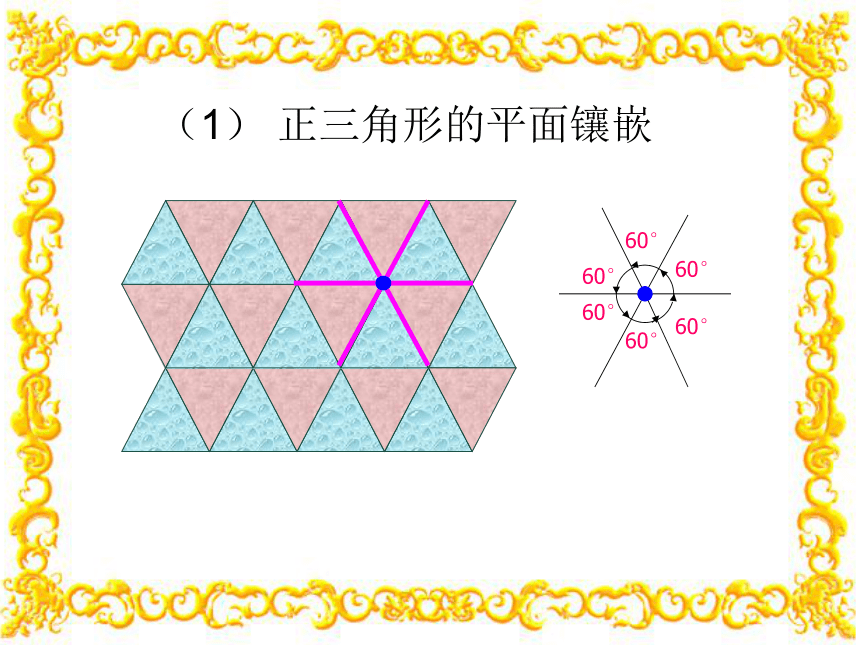
(1) 正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
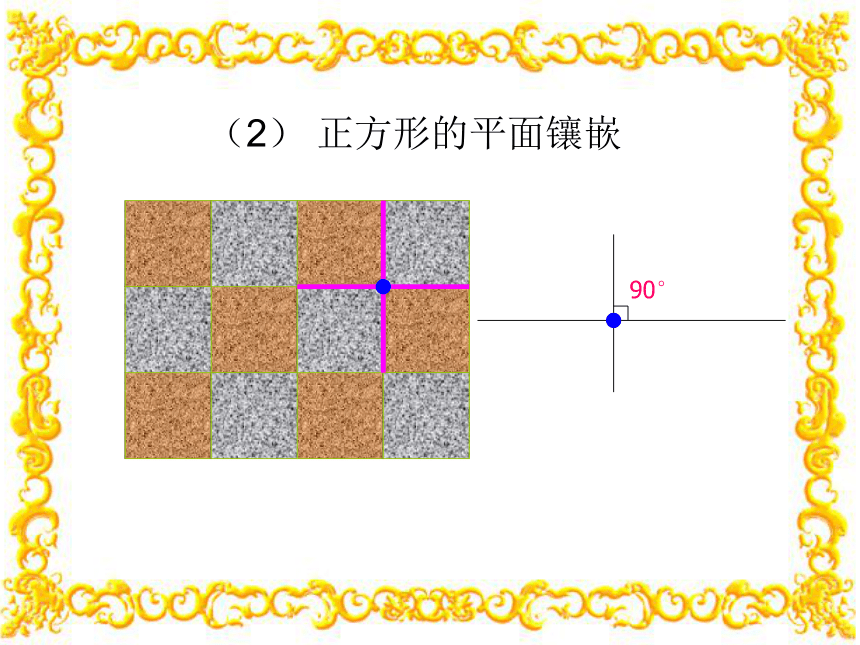
(2) 正方形的平面镶嵌
90°
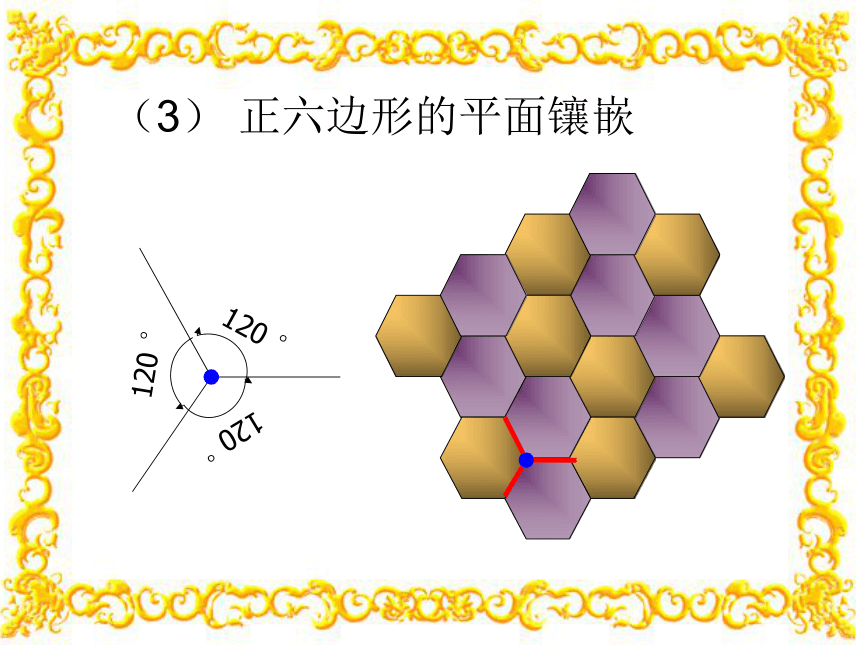
(3) 正六边形的平面镶嵌
120 °
120 °
120 °
你能只用正五边形镶嵌一个地面吗?
为什么正五边形不能镶嵌地面?而用正三角形可以?
因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。
而正三角形的内角为180 ° ,两个180 °为360 ° ,正四边形的内角和为360 ° ,所以均可镶嵌成平面。
只用一种正多边形进行镶嵌,只有(6,6,6);(4,4,4,4);(3,3,3,3,3,3)三种情形。那么,如果用两种正多边形进行镶嵌呢?
1)试用正三角形与正方形进行平面镶嵌,用纸片进行实验
2)试用正三角形与正六边形进行平面镶嵌,用纸片进行拼图
分组活动
②
①
注意:同一个组合会有不同的镶嵌效果
120°
120°
60°
60°
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
正三角形和正五边形能否镶嵌
正三角形和正六边形能否镶嵌
正方形和正八边形能否镶嵌
正三角形与正六边形镶嵌
正方形与正八边形镶嵌
正十二边形与正三角形的平面镶嵌
正十二边形与正方形、正五边形的平面镶嵌
正八边形与正方形的平面镶嵌
不是正多边形的镶嵌
等腰三角形
平行四边形
矩 形
你能总结出多边形镶嵌的条件吗
当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就能镶嵌。
随堂练习
如图,在一个正方形的内部按图①的方式剪去一个正三角形,并平移,形成如图②所示的新图案.这个新图案为“基本图案”能否进行密铺 说说你的理由.
①
②
我们常见如图所示图案的地面,他们全用正方形或全用正六边形形状的材料铺成。
1、像这样铺地面,能否全用正五边形材料呢?为什么?
2、请你画一个用两种不同的正多边形材料铺地的草图。
谢谢!
课题学习——镶嵌
用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面(或平面镶嵌)。
请你观察
你能只用一种正多边形(如正三角形,正四边形,正六边形)拼成一个地面吗?(用自制的正三角形,正方形,正六边形纸片进行实验)
问题1:如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面?
仅用正多边形进行镶嵌,要嵌成一个平面,必须要求在公共顶点上所有内角和为360 。
(1) 正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
(2) 正方形的平面镶嵌
90°
(3) 正六边形的平面镶嵌
120 °
120 °
120 °
你能只用正五边形镶嵌一个地面吗?
为什么正五边形不能镶嵌地面?而用正三角形可以?
因为正五边形的内角不能组成360°的角,而正三角形的内角能组成360°的角。
而正三角形的内角为180 ° ,两个180 °为360 ° ,正四边形的内角和为360 ° ,所以均可镶嵌成平面。
只用一种正多边形进行镶嵌,只有(6,6,6);(4,4,4,4);(3,3,3,3,3,3)三种情形。那么,如果用两种正多边形进行镶嵌呢?
1)试用正三角形与正方形进行平面镶嵌,用纸片进行实验
2)试用正三角形与正六边形进行平面镶嵌,用纸片进行拼图
分组活动
②
①
注意:同一个组合会有不同的镶嵌效果
120°
120°
60°
60°
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
正三角形和正五边形能否镶嵌
正三角形和正六边形能否镶嵌
正方形和正八边形能否镶嵌
正三角形与正六边形镶嵌
正方形与正八边形镶嵌
正十二边形与正三角形的平面镶嵌
正十二边形与正方形、正五边形的平面镶嵌
正八边形与正方形的平面镶嵌
不是正多边形的镶嵌
等腰三角形
平行四边形
矩 形
你能总结出多边形镶嵌的条件吗
当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就能镶嵌。
随堂练习
如图,在一个正方形的内部按图①的方式剪去一个正三角形,并平移,形成如图②所示的新图案.这个新图案为“基本图案”能否进行密铺 说说你的理由.
①
②
我们常见如图所示图案的地面,他们全用正方形或全用正六边形形状的材料铺成。
1、像这样铺地面,能否全用正五边形材料呢?为什么?
2、请你画一个用两种不同的正多边形材料铺地的草图。
谢谢!
