苏科版数学九年级上册 2.5直线与圆的位置关系 课件1(18张PPT)
文档属性
| 名称 | 苏科版数学九年级上册 2.5直线与圆的位置关系 课件1(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 06:08:57 | ||
图片预览





文档简介
(共18张PPT)
2.5
直线与圆的位置关系(1)
通过前面知识的学习,我们已经知道了点和圆的位置关系共有
种,分别是
.
【猜想】若将点换成一条直线,你能猜想直线与圆的位置之间有几种不同的位置关系吗?
温故而知新
【验证】在纸上画一条直线,把硬币边缘看作圆,在纸上移动硬币.
【思维点拨】同学们可以通过观察直尺移动的过程中,直尺与圆之间公共点个数的变化来确定直线与圆之间的不同位置关系.
a(直线)
●O
●O
●O
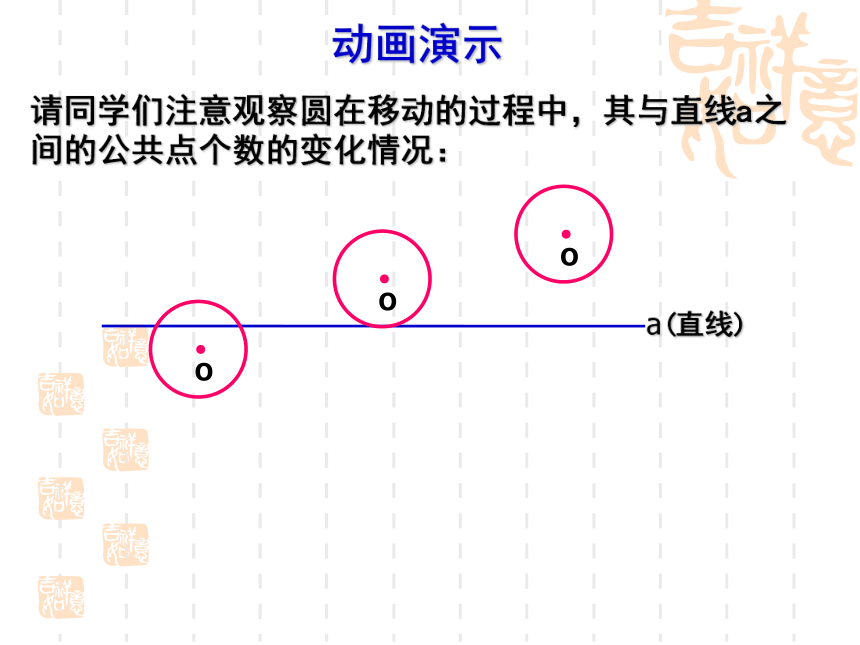
动画演示
请同学们注意观察圆在移动的过程中,其与直线a之间的公共点个数的变化情况:
(1)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(2)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线.
(3)直线和圆没有公共点时,叫做直线和圆相离.
归纳新知
直线与圆的位置关系(用公共点的个数来区分)
海边日出
看图判断直线a与⊙O的位置关系:
(1)
(2)
(3)
相离
相交
a
a
●O
●O
●O
如果公共点的个数不好判断,又该怎么判断直线与圆的位置关系呢?
【思维点拨】“直线和圆的位置关系”能否像“点和圆的位置关系”一样,可以用数量关系来刻画它们的三种位置关系呢?
探究活动
相切
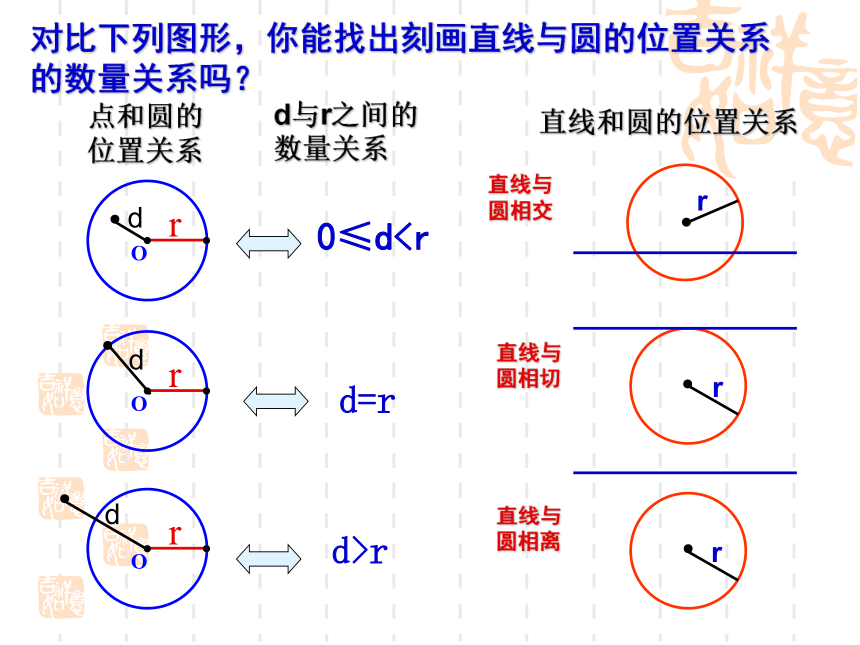
点和圆的位置关系
d与r之间的数量关系
0≤dr
O
d
●
d=r
r
O
d
●
d>r
r
O
d
●
直线和圆的位置关系
直线与圆相交
●
r
直线与圆相切
r
●
直线与圆相离
●
r
对比下列图形,你能找出刻画直线与圆的位置关系的数量关系吗?
d
r
相交
N
●O
M
d
r
相切
C
D
●
O
相离
d
●O
r
A
H
直线与圆相离
d>r
直线与圆相切
d=r
直线与圆相交
d归纳新知
例1.已知圆的直径为12cm,设直线和圆心的距离为d:
(2)若直线与圆相离,则d的取值范围为
.
(1)若直线与圆只有一个公共点,则d=
;
若d=4.5cm,则直线与圆 ;
相交
6cm
【变式训练】
d>6cm
新知识应用
例2.在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)r=2;(2)r=
;(3)r=3.
A
C
B
D
d
1.填表:
d
r
●
O
图形
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称
直线的名称
巩固练习
r
d
●
O
r
d
O
●
2.已知⊙O的直径为4,圆心O到直线l的距离为3.
则直线l与⊙O的位置关系是
.
3.Rt△ABC中,∠C=900,AB=10,AC=6,以C为圆心作⊙C,则⊙C的半径为
时,
⊙C与AB相切.
4.已知⊙O的直径为10,点O到直线l距离为d.
(1)若直线l与⊙O相切,则d=
;
(2)若d=4,则直线l与⊙O的位置关系是
;
(3)若d=6,则直线l与⊙O有
个公共点.
课堂小结
1.直线与圆的位置关系:
d
r
●
O
r
d
●
O
r
d
O
●
图形
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称
直线的名称
相交
2
d相切
1
d=r
切点
切线
相离
0
d>r
判定直线与圆的位置关系的方法有
种:
(1)根据定义,由
的个数来判断;
(2)根据性质,由
的关系来判断.
在实际解题中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
2.思维点拨:
例.如图,∠AOB=300,M为射线OB上一点,以M为圆心,2cm长为半径作圆,如果OM=6cm,那么OA与⊙M有何位置关系?
●
M
A
O
B
【思维变式】若M在射线OB上运动,问:
①当OM满足
时,⊙M与直线OA相切?
②当OM满足
时,⊙M与直线OA相交?
N
d
拓展提高
2.在△ABC中,AB=5,BC=4,AC=3,以C为圆心,r为半径画⊙C
.
(1)当r=2时,直线AB与⊙C的位置关系如何?
(2)若直线AB与⊙C相切,试求r的值.
(3)若直线AB与⊙C相交,试求r的取值范围.
(4)若⊙C与线段AB没有公共点,试求r的取值范围.
1.直线l上的一点到圆心O的距离等于⊙O的半径.则直线l与⊙O的位置关系是
.
巩固练习
3.如图,直线
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是(
)
A.2
B.3
C.4
D.5
易错题:
1.判断正误
1)与圆有公共点的直线是圆的切线
(
)
2)过圆外一点画一条直线,则直线与圆相离(
)
3)过圆内一点画一条直线,则直线与圆相交(
)
×
×
√
2.设⊙O的半径为3,直线a上一点到圆心的距离为3,则直线a与⊙O的位置关系是(
)
(A)相交
(B)相切
(C)相离
(D)相切或相交
D
2.5
直线与圆的位置关系(1)
通过前面知识的学习,我们已经知道了点和圆的位置关系共有
种,分别是
.
【猜想】若将点换成一条直线,你能猜想直线与圆的位置之间有几种不同的位置关系吗?
温故而知新
【验证】在纸上画一条直线,把硬币边缘看作圆,在纸上移动硬币.
【思维点拨】同学们可以通过观察直尺移动的过程中,直尺与圆之间公共点个数的变化来确定直线与圆之间的不同位置关系.
a(直线)
●O
●O
●O
动画演示
请同学们注意观察圆在移动的过程中,其与直线a之间的公共点个数的变化情况:
(1)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点.
(2)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线.
(3)直线和圆没有公共点时,叫做直线和圆相离.
归纳新知
直线与圆的位置关系(用公共点的个数来区分)
海边日出
看图判断直线a与⊙O的位置关系:
(1)
(2)
(3)
相离
相交
a
a
●O
●O
●O
如果公共点的个数不好判断,又该怎么判断直线与圆的位置关系呢?
【思维点拨】“直线和圆的位置关系”能否像“点和圆的位置关系”一样,可以用数量关系来刻画它们的三种位置关系呢?
探究活动
相切
点和圆的位置关系
d与r之间的数量关系
0≤d
O
d
●
d=r
r
O
d
●
d>r
r
O
d
●
直线和圆的位置关系
直线与圆相交
●
r
直线与圆相切
r
●
直线与圆相离
●
r
对比下列图形,你能找出刻画直线与圆的位置关系的数量关系吗?
d
r
相交
N
●O
M
d
r
相切
C
D
●
O
相离
d
●O
r
A
H
直线与圆相离
d>r
直线与圆相切
d=r
直线与圆相交
d
例1.已知圆的直径为12cm,设直线和圆心的距离为d:
(2)若直线与圆相离,则d的取值范围为
.
(1)若直线与圆只有一个公共点,则d=
;
若d=4.5cm,则直线与圆 ;
相交
6cm
【变式训练】
d>6cm
新知识应用
例2.在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1)r=2;(2)r=
;(3)r=3.
A
C
B
D
d
1.填表:
d
r
●
O
图形
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称
直线的名称
巩固练习
r
d
●
O
r
d
O
●
2.已知⊙O的直径为4,圆心O到直线l的距离为3.
则直线l与⊙O的位置关系是
.
3.Rt△ABC中,∠C=900,AB=10,AC=6,以C为圆心作⊙C,则⊙C的半径为
时,
⊙C与AB相切.
4.已知⊙O的直径为10,点O到直线l距离为d.
(1)若直线l与⊙O相切,则d=
;
(2)若d=4,则直线l与⊙O的位置关系是
;
(3)若d=6,则直线l与⊙O有
个公共点.
课堂小结
1.直线与圆的位置关系:
d
r
●
O
r
d
●
O
r
d
O
●
图形
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称
直线的名称
相交
2
d
1
d=r
切点
切线
相离
0
d>r
判定直线与圆的位置关系的方法有
种:
(1)根据定义,由
的个数来判断;
(2)根据性质,由
的关系来判断.
在实际解题中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
2.思维点拨:
例.如图,∠AOB=300,M为射线OB上一点,以M为圆心,2cm长为半径作圆,如果OM=6cm,那么OA与⊙M有何位置关系?
●
M
A
O
B
【思维变式】若M在射线OB上运动,问:
①当OM满足
时,⊙M与直线OA相切?
②当OM满足
时,⊙M与直线OA相交?
N
d
拓展提高
2.在△ABC中,AB=5,BC=4,AC=3,以C为圆心,r为半径画⊙C
.
(1)当r=2时,直线AB与⊙C的位置关系如何?
(2)若直线AB与⊙C相切,试求r的值.
(3)若直线AB与⊙C相交,试求r的取值范围.
(4)若⊙C与线段AB没有公共点,试求r的取值范围.
1.直线l上的一点到圆心O的距离等于⊙O的半径.则直线l与⊙O的位置关系是
.
巩固练习
3.如图,直线
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是(
)
A.2
B.3
C.4
D.5
易错题:
1.判断正误
1)与圆有公共点的直线是圆的切线
(
)
2)过圆外一点画一条直线,则直线与圆相离(
)
3)过圆内一点画一条直线,则直线与圆相交(
)
×
×
√
2.设⊙O的半径为3,直线a上一点到圆心的距离为3,则直线a与⊙O的位置关系是(
)
(A)相交
(B)相切
(C)相离
(D)相切或相交
D
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
