3.3.2指数函数的图象和性质(第三 课时) 课件(共38张PPT)——2021-2022学年高一上学期数学北师大版(2019)必修第一册
文档属性
| 名称 | 3.3.2指数函数的图象和性质(第三 课时) 课件(共38张PPT)——2021-2022学年高一上学期数学北师大版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 16:39:57 | ||
图片预览









文档简介
3.3.2指数函数的图像和性质
第三课时
教学目标
1.含指数函数单调性的判断方法,引入【复合函数单调性判断方法】
2.含指数函数单调性的应用:比较大小、解不等式、求值域等.
含指数函数的单调性的应用
重点
难点
复合函数单调性判断方法
环节一
单调性判断和证明
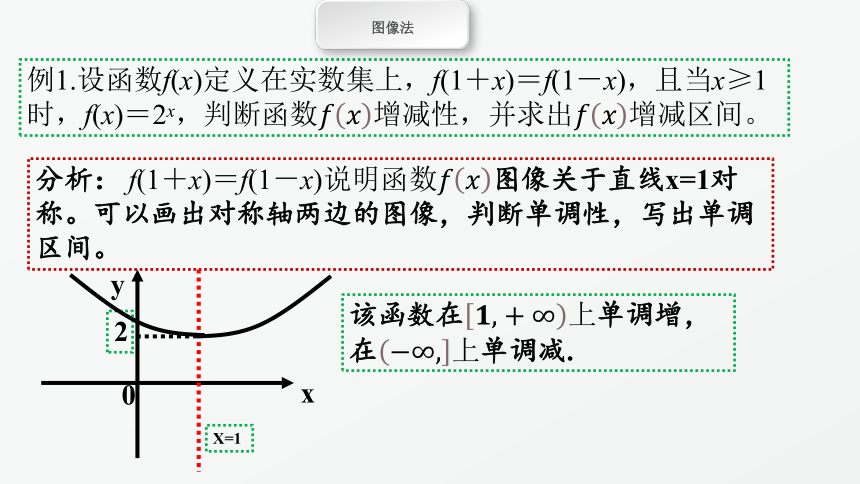
例1.设函数f(x)定义在实数集上,f(1+x)=f(1-x),且当x≥1时,f(x)=2x,判断函数????????增减性,并求出????????增减区间。
?
图像法
分析: f(1+x)=f(1-x)说明函数????????图像关于直线x=1对称。可以画出对称轴两边的图像,判断单调性,写出单调区间。
?
x
y
0
X=1
2
该函数在????,+∞上单调增,在?
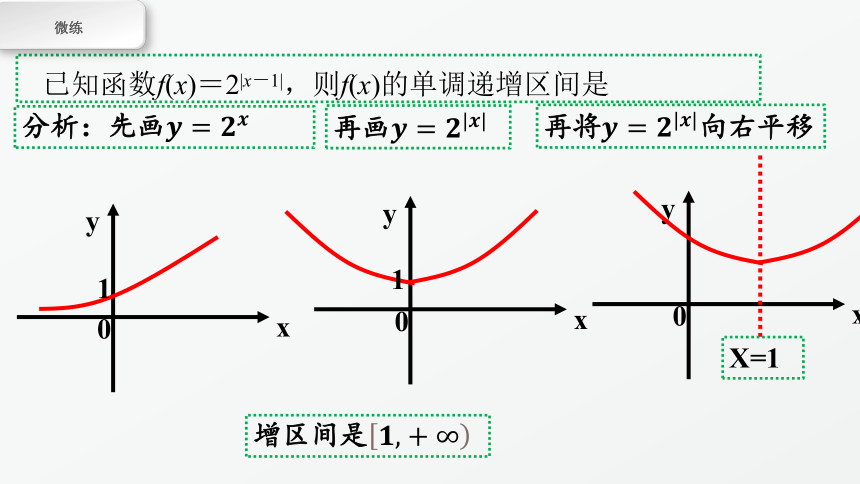
已知函数f(x)=2|x-1|,则f(x)的单调递增区间是
分析:先画????=????????
?
x
0
y
再画????=????|????|
?
1
x
0
y
1
再将????=????|????|向右平移
?
x
0
y
X=1
增区间是????,+∞
?
微练
定义法
例2.已知函数f(x)=?????12????+1(x∈R).
用定义证明:不论a为何实数,f(x)在(-∞,+∞)上为增函数;
?
解:(1)证明:f(x)的定义域为R,
设x1,x2是R上的任意两个不相等的实数,且x1?????????????????????????=?????????????????????????????????????+
提示
用定义判证含指数函数单调性时,在比较大小阶段,要处理好指数函数的单调性,比如????????????,????????????大小关系,????????????????,????????????????大小关系。
?
性质法
法则一
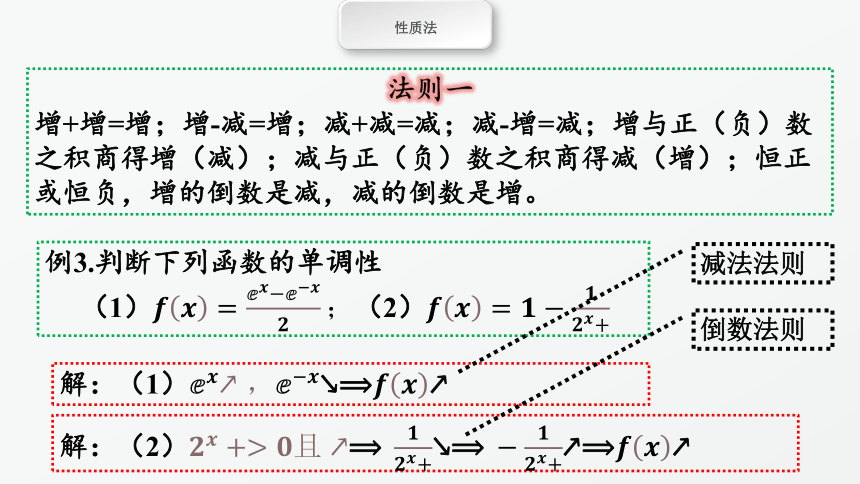
增+增=增;增-减=增;减+减=减;减-增=减;增与正(负)数之积商得增(减);减与正(负)数之积商得减(增);恒正或恒负,增的倒数是减,减的倒数是增。
例3.判断下列函数的单调性
(1)????????=????????????????;(2)????????=?????????????????+
性质法
例4.函数y=?????????????????????????+????的单调递增区间是 .
?
解析:(1)令t=x2-2x+3,则由一元二次函数的性质可知该函数在(-∞,1]上单调递减,且y=????????????为减函数,故函数y=?????????????????????????+????的单调递增区间为(-∞,1].
?
指数型复合函数的单调性的求解步骤:
(1)求定义域:依据题意明确研究范围.
(2)拆分:把原函数拆分成几个基本函数.
(3)定性质:分层逐一求单调性.
(4)下结论:根据复合函数的单调性法则即“同增异减”,得出原函数的单调性.
性质法
法则二
例5.判断y=?????????????????????的单调性
?
解:令u=x2-2x,则原函数变为y=3u.
∵u=x2-2x=(x-1)2-1在区间(-∞,1]上单调递减,
在区间[1,+∞)上单调递增,
又∵y=3u在(-∞,+∞)上为增函数,
∴y=?????????????????????在区间(-∞,1]上单调递减,在区间[1,+∞)上单调递增.
?
函数y=?????????????????的单调递增区间为( )
A.(-∞,+∞) B.(0,+∞)
C.(1,+∞) D.(0,1)
?
微练
分析:上面两例题侧重于指数与二次函数复合,此题是指数与一次函数复合,方法一样:【同增异减】
解析:函数的定义域为R.设u=1-x,y=????????????,
∵u=1-x在R上为减函数,y=????????????在R上为减函数,
∴y=?????????????????在R上是增函数.
?
经验一
复合函数单调性使用性质法则时
1.先求定义域。这一点学生经常忘;
2.同增异减,内外搭配
环节二
单调性求参
例6.若函数f(x)=????????,????≥13?????2????+1,????<1是R上的增函数,则实数a的取值范围为
?
解析:为了保证在R上增,两增且后段不低于前段.
????>????,?????????????>????,????≥
环节三
单调性求最值
例7.函数y=ax(a>0,且a≠1)在区间[0,1]上的最大值与最小值的差为5,则a= .?
解析:当a>1时,有a1-a0=5,即a=6;
当0综上知,a=6.
答案:6
例8.已知函数 y=?????????????????????????, 求其值域.
?
提示:先利用【同增异减】判断其单调性,然后,利用单调性求值域
解:令u=x2-2x,则原函数变为y=????????u.
∵u=x2-2x=(x-1)2-1在区间(-∞,1]上单调递减,
在区间[1,+∞)上单调递增,又∵ y=????????u在(-∞,+∞)上为减函数,
∴ y=?????????????????????????在区间(-∞,1]上单调递增,在区间[1,+∞)上单调递减.
∵u=x2-2x=(x-1)2-1≥-1,∴ ????????u ≤2,∴原函数的值域为?∞,
求函数y=12????2?2????+2(0≤x≤3)的值域
?
微练
提示:为了减化复合函数求值域过程,可以用换元法,把内层函数的值域求出,再根据【内增异减】原则,处理好添加底数后,值域的情况。
[解] 令t=x2-2x+2,则y=12????,又t=x2-2x+2=(x-1)2+1,0≤x≤3,∴当x=1时,tmin=1;当x=3时,tmax=5.故1≤t≤5,∴132≤y≤15,故所求函数的值域为132,15.
?
例9.函数f(x)=12????-3x在区间[-1,1]上的最大值为________
?
解: 12????↘, 3????↗,????(????)↘,最大值是????
环节四
单调性比大小
例10.下列正确的是( )
????
例11.若3m+2-n≥3n+2-m则( )
A.m+n≥0 B.m+n≤0
C.m-n≥0 D.m-n≤0
解:3m+2-n≥3n+2-m?3m-2-m≥3n-2-n.
又f(x)=3x-2-x是增函数,f(m)≥f(n),
则m≥n,即m-n≥0
经验二
上述两个比较大小题共性特点
1.构造同名函数;
2.判断单调性;
3.比大小
环节五
单调性解不等式
例12(1)解不等式?????????????????????≤2;
(2)若a-3x>ax+4(a>1),求实数x的取值范围.
?
角度一 代数不等式
分析:先化为同底数的幂→根据指数函数的单调性建立不等式求解→结果要写成集合或区间的形式
解:(1)∵2=?????????????,∴原不等式可以转化为?????????????????????≤?????????????.
∵y=????????????在R上是减函数,∴3x-1≥-1,得x≥0.
故原不等式的解集是{x|x≥0}.
?
例12(1)解不等式?????????????????????≤2;
(2)若a-3x>ax+4(a>1),求实数x的取值范围.
?
角度一 代数不等式
分析:先化为同底数的幂→根据指数函数的单调性建立不等式求解→结果要写成集合或区间的形式
(2)∵f(x)=ax(a>1)是R上的增函数,且a-3x>ax+4,
∴-3x>x+4,得x<-1,
故实数x的取值范围是{x|x<-1}.
1.若把本例(2)中的“a>1”换为“0微练
解:因为0又a-3x>ax+4,所以-3x-1,
故实数x的取值范围是{x|x>-1}.
2. 若把本例(2)中的“a>1”换为“a>0,且a≠1”,其他条件不变,求实数x的取值范围.
微练
解:当a>1时,原不等式?-3x>x+4?x<-1,
当0-1,
故当a>1时,实数x的取值范围是{x|x<-1},
当0-1}.
例13.解关于x的不等式?????????????????????>?????????????+????(a>0,且a≠1).
?
错解 ∵a>0,∴由?????????????????????>?????????????+????,得
x2-3x>-x2+2,即2x2-3x-2>0,解得x>2,或x<-????????.
?
错因本题有两处错误,一是a>0,不能保证f(x)=ax在R上是增函数;二是不等式的解集没有写成集合的形式.
正解:设f(x)=ax(a>0,且a≠1).
当a>1时,f(x)在R上是增函数,由?????????????????????>?????????????+????,得x2-3x>-x2+2,
即2x2-3x-2>0,解得x>2,或x<-????????.
当0?????????????+????,得x2-3x<-x2+2,
即2x2-3x-2<0,
解得-???????? 综上,当a>1时,不等式的解集为????????????;
当0?
经验三
解不等式af(x)>ag(x)(a>0,且a≠1)的依据是指数型函数的单调性,要养成判断底数取值范围的习惯,若底数不确定,就需进行分类讨论,即af(x)>ag(x)?????(????)>????(????),????>????,????(????)?
角度二 函数不等式
例14.已知定义域为R的函数f(x)=1?2????2????+1+2.
(1)判断奇偶性和单调性;
(2)若对于任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
?
奇偶性
奇(略)
增减性
R上为减函数(略)
∵f(x)为奇函数,
∴f(t2-2t)+f(2t2-k)<0,
即f(t2-2t)<-f(2t2-k)=f(-2t2+k).
又∵f(x)在R上为减函数,
∴t2-2t>-2t2+k,即对一切t∈R,有3t2-2t-k>0,
∴Δ<0,即4+12k<0,
∴k<-13.
故k的取值范围是?∞,?13.
?
经验四
解不等式f????1.不符合上面标准形式,要化为标准形式;
2.研究清楚函数的单调性(在哪个区间增,在哪个区间减,不能笼统地说增与减)
3.运用单调性脱f,化成代数不等式。
?
课堂小结
1.核心要点
1.单调性的判断三种方法归纳
2.单调性应用
2.数学素养
体会数学抽象的过程,强化直观想象素养的培养.
谢谢观看
第三课时
教学目标
1.含指数函数单调性的判断方法,引入【复合函数单调性判断方法】
2.含指数函数单调性的应用:比较大小、解不等式、求值域等.
含指数函数的单调性的应用
重点
难点
复合函数单调性判断方法
环节一
单调性判断和证明
例1.设函数f(x)定义在实数集上,f(1+x)=f(1-x),且当x≥1时,f(x)=2x,判断函数????????增减性,并求出????????增减区间。
?
图像法
分析: f(1+x)=f(1-x)说明函数????????图像关于直线x=1对称。可以画出对称轴两边的图像,判断单调性,写出单调区间。
?
x
y
0
X=1
2
该函数在????,+∞上单调增,在?
已知函数f(x)=2|x-1|,则f(x)的单调递增区间是
分析:先画????=????????
?
x
0
y
再画????=????|????|
?
1
x
0
y
1
再将????=????|????|向右平移
?
x
0
y
X=1
增区间是????,+∞
?
微练
定义法
例2.已知函数f(x)=?????12????+1(x∈R).
用定义证明:不论a为何实数,f(x)在(-∞,+∞)上为增函数;
?
解:(1)证明:f(x)的定义域为R,
设x1,x2是R上的任意两个不相等的实数,且x1
提示
用定义判证含指数函数单调性时,在比较大小阶段,要处理好指数函数的单调性,比如????????????,????????????大小关系,????????????????,????????????????大小关系。
?
性质法
法则一
增+增=增;增-减=增;减+减=减;减-增=减;增与正(负)数之积商得增(减);减与正(负)数之积商得减(增);恒正或恒负,增的倒数是减,减的倒数是增。
例3.判断下列函数的单调性
(1)????????=????????????????;(2)????????=?????????????????+
性质法
例4.函数y=?????????????????????????+????的单调递增区间是 .
?
解析:(1)令t=x2-2x+3,则由一元二次函数的性质可知该函数在(-∞,1]上单调递减,且y=????????????为减函数,故函数y=?????????????????????????+????的单调递增区间为(-∞,1].
?
指数型复合函数的单调性的求解步骤:
(1)求定义域:依据题意明确研究范围.
(2)拆分:把原函数拆分成几个基本函数.
(3)定性质:分层逐一求单调性.
(4)下结论:根据复合函数的单调性法则即“同增异减”,得出原函数的单调性.
性质法
法则二
例5.判断y=?????????????????????的单调性
?
解:令u=x2-2x,则原函数变为y=3u.
∵u=x2-2x=(x-1)2-1在区间(-∞,1]上单调递减,
在区间[1,+∞)上单调递增,
又∵y=3u在(-∞,+∞)上为增函数,
∴y=?????????????????????在区间(-∞,1]上单调递减,在区间[1,+∞)上单调递增.
?
函数y=?????????????????的单调递增区间为( )
A.(-∞,+∞) B.(0,+∞)
C.(1,+∞) D.(0,1)
?
微练
分析:上面两例题侧重于指数与二次函数复合,此题是指数与一次函数复合,方法一样:【同增异减】
解析:函数的定义域为R.设u=1-x,y=????????????,
∵u=1-x在R上为减函数,y=????????????在R上为减函数,
∴y=?????????????????在R上是增函数.
?
经验一
复合函数单调性使用性质法则时
1.先求定义域。这一点学生经常忘;
2.同增异减,内外搭配
环节二
单调性求参
例6.若函数f(x)=????????,????≥13?????2????+1,????<1是R上的增函数,则实数a的取值范围为
?
解析:为了保证在R上增,两增且后段不低于前段.
????>????,?????????????>????,????≥
环节三
单调性求最值
例7.函数y=ax(a>0,且a≠1)在区间[0,1]上的最大值与最小值的差为5,则a= .?
解析:当a>1时,有a1-a0=5,即a=6;
当0
答案:6
例8.已知函数 y=?????????????????????????, 求其值域.
?
提示:先利用【同增异减】判断其单调性,然后,利用单调性求值域
解:令u=x2-2x,则原函数变为y=????????u.
∵u=x2-2x=(x-1)2-1在区间(-∞,1]上单调递减,
在区间[1,+∞)上单调递增,又∵ y=????????u在(-∞,+∞)上为减函数,
∴ y=?????????????????????????在区间(-∞,1]上单调递增,在区间[1,+∞)上单调递减.
∵u=x2-2x=(x-1)2-1≥-1,∴ ????????u ≤2,∴原函数的值域为?∞,
求函数y=12????2?2????+2(0≤x≤3)的值域
?
微练
提示:为了减化复合函数求值域过程,可以用换元法,把内层函数的值域求出,再根据【内增异减】原则,处理好添加底数后,值域的情况。
[解] 令t=x2-2x+2,则y=12????,又t=x2-2x+2=(x-1)2+1,0≤x≤3,∴当x=1时,tmin=1;当x=3时,tmax=5.故1≤t≤5,∴132≤y≤15,故所求函数的值域为132,15.
?
例9.函数f(x)=12????-3x在区间[-1,1]上的最大值为________
?
解: 12????↘, 3????↗,????(????)↘,最大值是????
环节四
单调性比大小
例10.下列正确的是( )
????
例11.若3m+2-n≥3n+2-m则( )
A.m+n≥0 B.m+n≤0
C.m-n≥0 D.m-n≤0
解:3m+2-n≥3n+2-m?3m-2-m≥3n-2-n.
又f(x)=3x-2-x是增函数,f(m)≥f(n),
则m≥n,即m-n≥0
经验二
上述两个比较大小题共性特点
1.构造同名函数;
2.判断单调性;
3.比大小
环节五
单调性解不等式
例12(1)解不等式?????????????????????≤2;
(2)若a-3x>ax+4(a>1),求实数x的取值范围.
?
角度一 代数不等式
分析:先化为同底数的幂→根据指数函数的单调性建立不等式求解→结果要写成集合或区间的形式
解:(1)∵2=?????????????,∴原不等式可以转化为?????????????????????≤?????????????.
∵y=????????????在R上是减函数,∴3x-1≥-1,得x≥0.
故原不等式的解集是{x|x≥0}.
?
例12(1)解不等式?????????????????????≤2;
(2)若a-3x>ax+4(a>1),求实数x的取值范围.
?
角度一 代数不等式
分析:先化为同底数的幂→根据指数函数的单调性建立不等式求解→结果要写成集合或区间的形式
(2)∵f(x)=ax(a>1)是R上的增函数,且a-3x>ax+4,
∴-3x>x+4,得x<-1,
故实数x的取值范围是{x|x<-1}.
1.若把本例(2)中的“a>1”换为“0
解:因为0
故实数x的取值范围是{x|x>-1}.
2. 若把本例(2)中的“a>1”换为“a>0,且a≠1”,其他条件不变,求实数x的取值范围.
微练
解:当a>1时,原不等式?-3x>x+4?x<-1,
当0
故当a>1时,实数x的取值范围是{x|x<-1},
当0
例13.解关于x的不等式?????????????????????>?????????????+????(a>0,且a≠1).
?
错解 ∵a>0,∴由?????????????????????>?????????????+????,得
x2-3x>-x2+2,即2x2-3x-2>0,解得x>2,或x<-????????.
?
错因本题有两处错误,一是a>0,不能保证f(x)=ax在R上是增函数;二是不等式的解集没有写成集合的形式.
正解:设f(x)=ax(a>0,且a≠1).
当a>1时,f(x)在R上是增函数,由?????????????????????>?????????????+????,得x2-3x>-x2+2,
即2x2-3x-2>0,解得x>2,或x<-????????.
当0
即2x2-3x-2<0,
解得-????????
当0
经验三
解不等式af(x)>ag(x)(a>0,且a≠1)的依据是指数型函数的单调性,要养成判断底数取值范围的习惯,若底数不确定,就需进行分类讨论,即af(x)>ag(x)?????(????)>????(????),????>????,????(????)?
角度二 函数不等式
例14.已知定义域为R的函数f(x)=1?2????2????+1+2.
(1)判断奇偶性和单调性;
(2)若对于任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
?
奇偶性
奇(略)
增减性
R上为减函数(略)
∵f(x)为奇函数,
∴f(t2-2t)+f(2t2-k)<0,
即f(t2-2t)<-f(2t2-k)=f(-2t2+k).
又∵f(x)在R上为减函数,
∴t2-2t>-2t2+k,即对一切t∈R,有3t2-2t-k>0,
∴Δ<0,即4+12k<0,
∴k<-13.
故k的取值范围是?∞,?13.
?
经验四
解不等式f????1.不符合上面标准形式,要化为标准形式;
2.研究清楚函数的单调性(在哪个区间增,在哪个区间减,不能笼统地说增与减)
3.运用单调性脱f,化成代数不等式。
?
课堂小结
1.核心要点
1.单调性的判断三种方法归纳
2.单调性应用
2.数学素养
体会数学抽象的过程,强化直观想象素养的培养.
谢谢观看
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
