人教版2021年八年级上册:12.1 全等三角形 同步练习卷(Word版含解析)
文档属性
| 名称 | 人教版2021年八年级上册:12.1 全等三角形 同步练习卷(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 195.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 00:00:00 | ||
图片预览

文档简介
人教版2021年八年级上册:12.1 全等三角形 同步练习卷
一.选择题
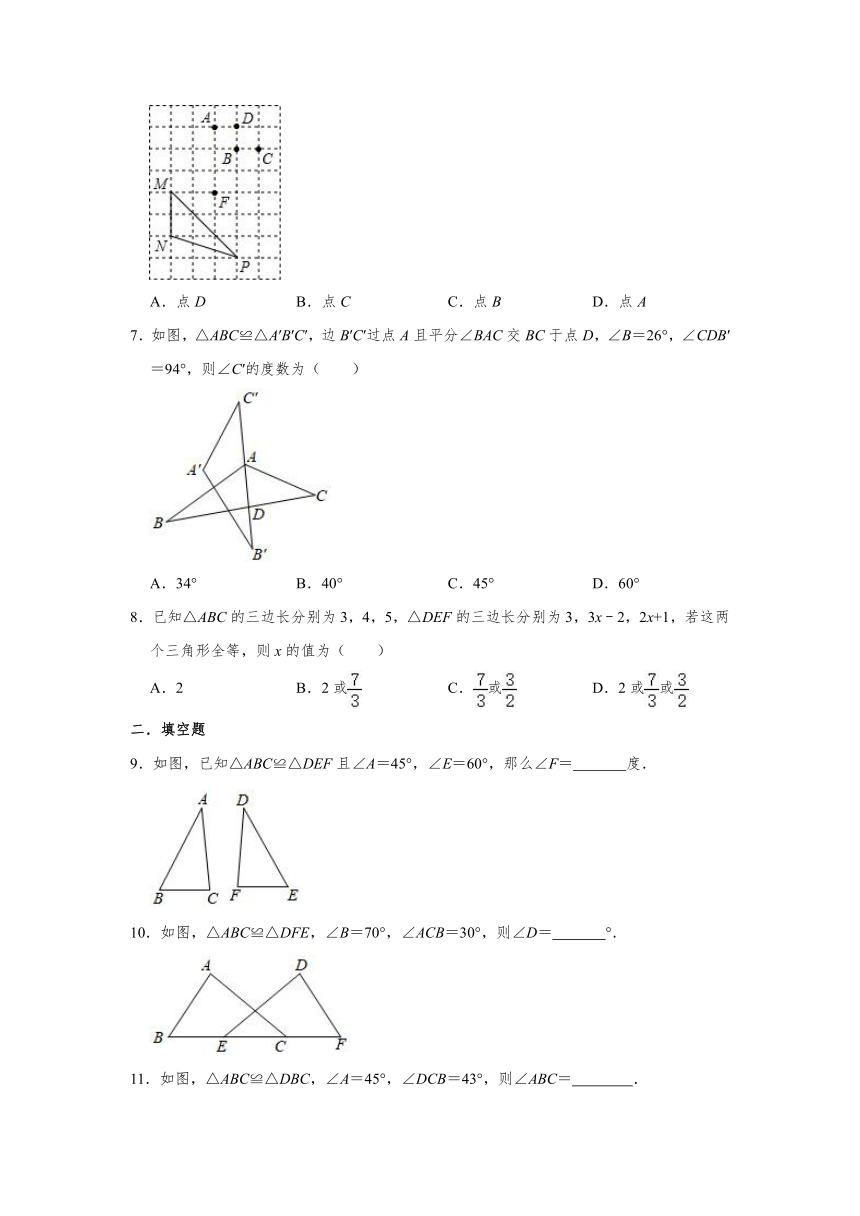
1.如图,△ABC≌△ADC,则与∠BAC相等的角是( )
A.∠ACD B.∠ADC C.∠DAC D.∠ACB
2.已知图中的两个三角形全等,则∠1等于( )
A.70° B.50° C.60° D.120°
3.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED B.∠BAD=∠CAE C.AB=AE D.AC=DE
4.如图,△ABC≌△EBD,AB=4,BD=7,则CE的长度为( )
A.1 B.2 C.3 D.4
5.已知△ABC≌△DEF,且△DEF的面积为18,BC=6,则BC边上的高等于( )
A.13 B.3 C.4 D.6
6.图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
7.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
8.已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A.2 B.2或 C.或 D.2或或
二.填空题
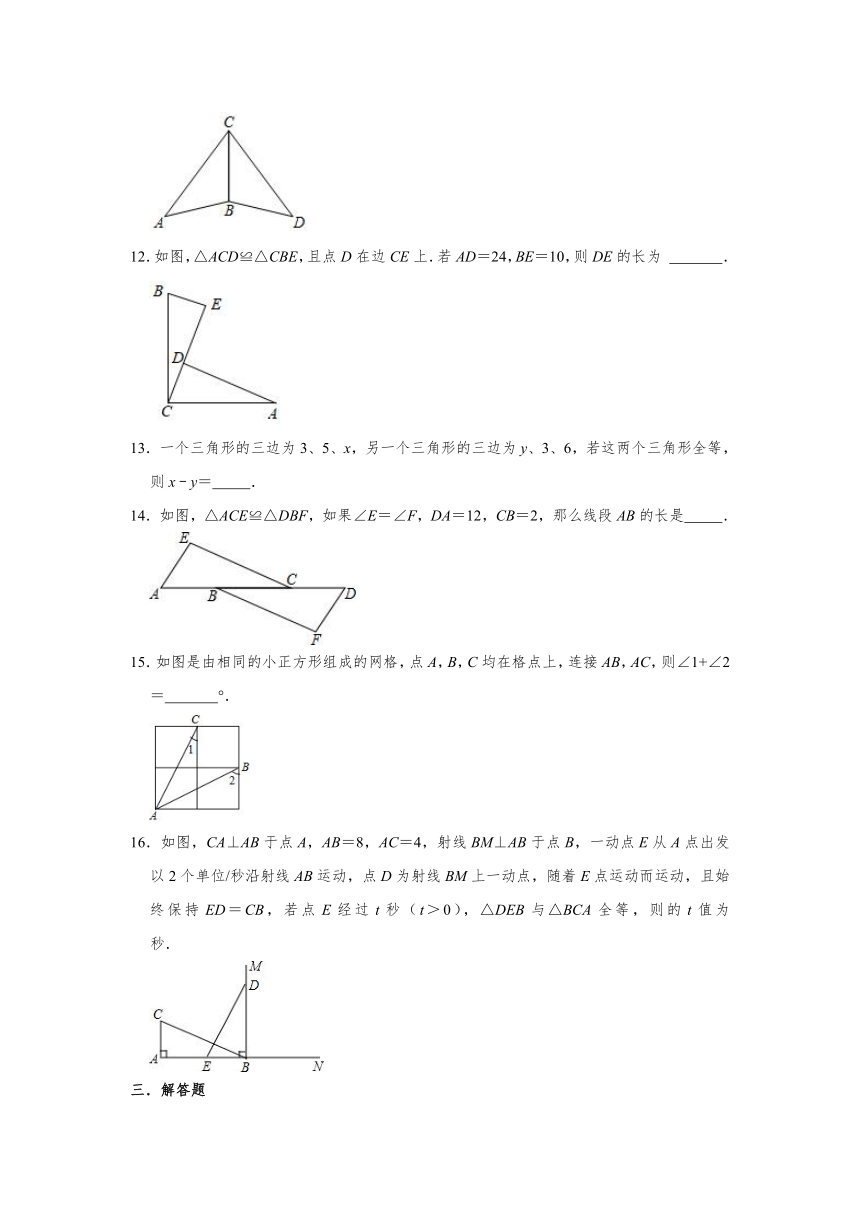
9.如图,已知△ABC≌△DEF且∠A=45°,∠E=60°,那么∠F= 度.
10.如图,△ABC≌△DFE,∠B=70°,∠ACB=30°,则∠D= °.
11.如图,△ABC≌△DBC,∠A=45°,∠DCB=43°,则∠ABC= .
12.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 .
13.一个三角形的三边为3、5、x,另一个三角形的三边为y、3、6,若这两个三角形全等,则x﹣y= .
14.如图,△ACE≌△DBF,如果∠E=∠F,DA=12,CB=2,那么线段AB的长是 .
15.如图是由相同的小正方形组成的网格,点A,B,C均在格点上,连接AB,AC,则∠1+∠2= °.
16.如图,CA⊥AB于点A,AB=8,AC=4,射线BM⊥AB于点B,一动点E从A点出发以2个单位/秒沿射线AB运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,若点E经过t秒(t>0),△DEB与△BCA全等,则的t值为 秒.
三.解答题
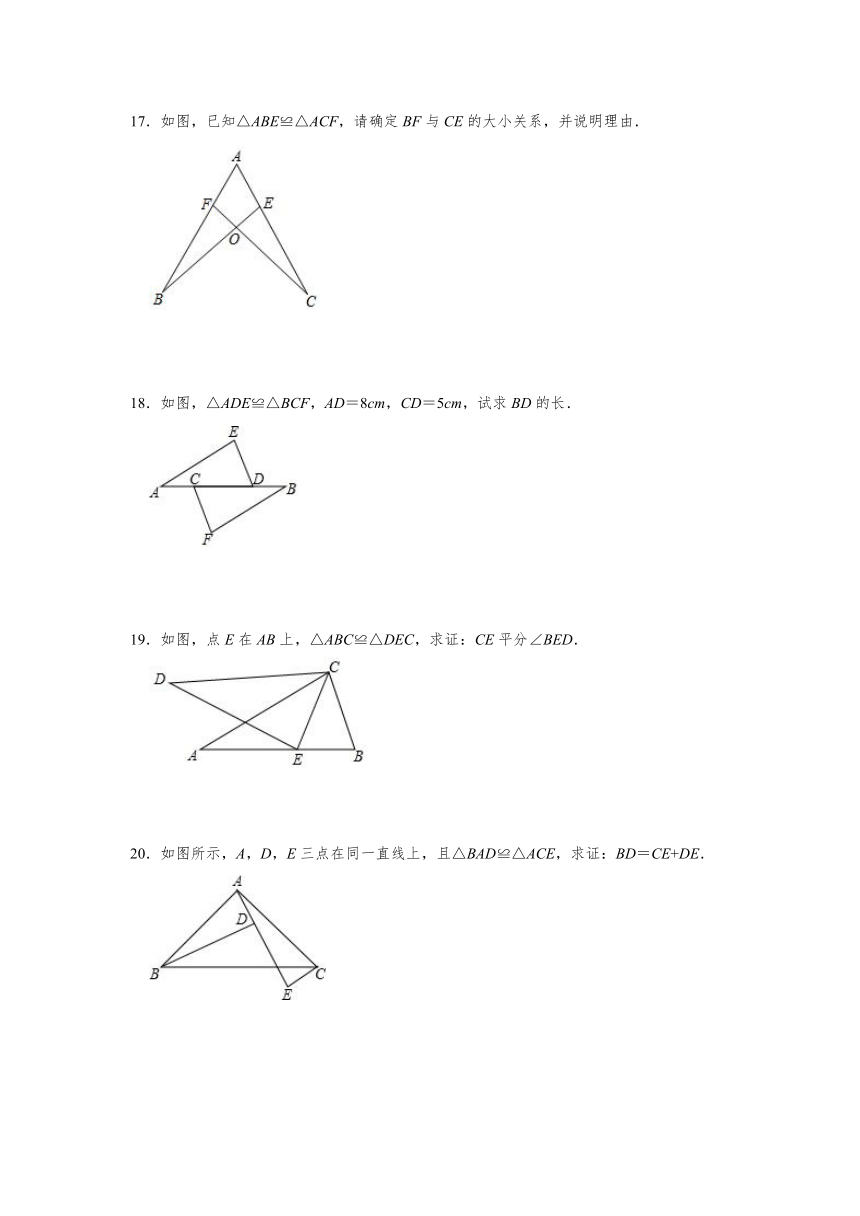
17.如图,已知△ABE≌△ACF,请确定BF与CE的大小关系,并说明理由.
18.如图,△ADE≌△BCF,AD=8cm,CD=5cm,试求BD的长.
19.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
20.如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE,求证:BD=CE+DE.
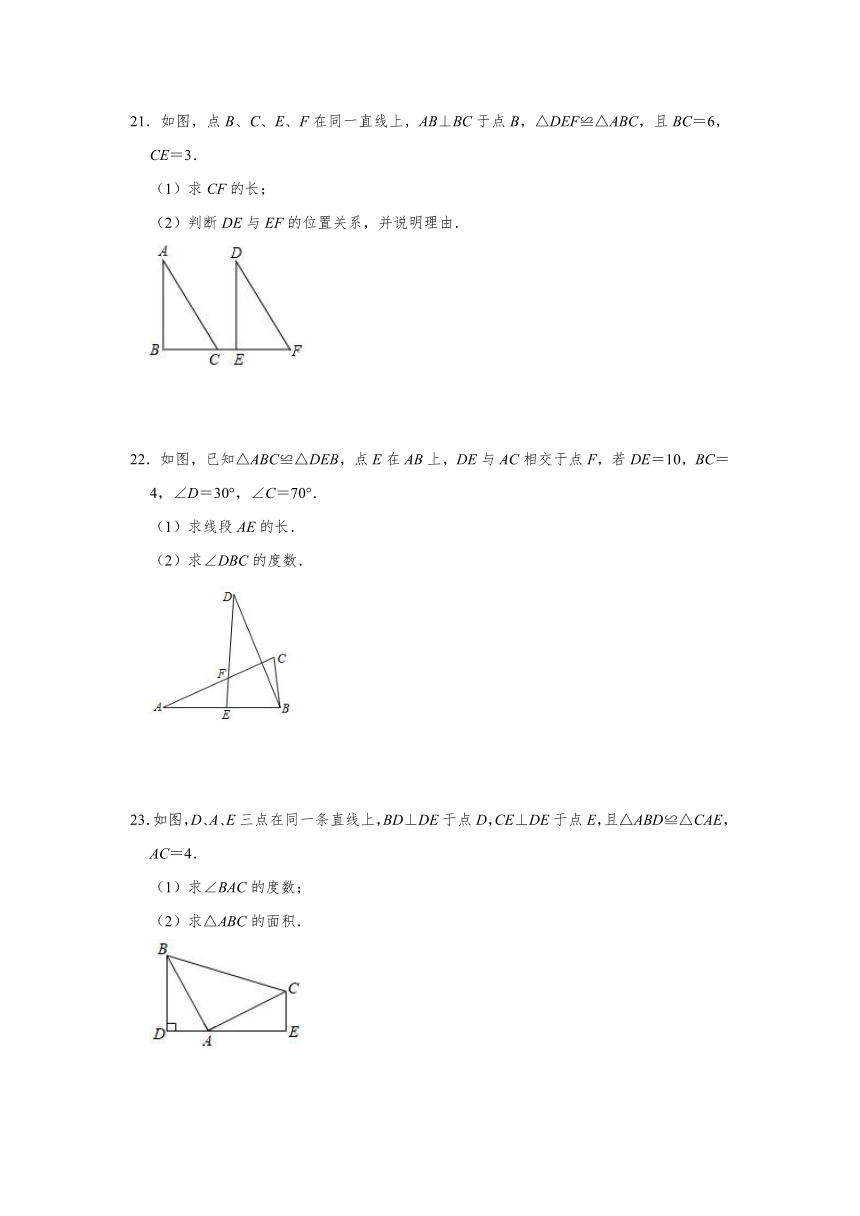
21.如图,点B、C、E、F在同一直线上,AB⊥BC于点B,△DEF≌△ABC,且BC=6,CE=3.
(1)求CF的长;
(2)判断DE与EF的位置关系,并说明理由.
22.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
23.如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)求△ABC的面积.
24.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
参考答案
一.选择题
1.解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
故选:C.
2.解:∵△ABC≌△DEF,
∴∠E=∠B=70°,
∴∠1=180°﹣50°﹣70°=60°,
故选:C.
3.解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
4.解:∵△ABC≌△EBD,
∴AB=BE=4,BC=BD=7,
∴EC=BC﹣BE=7﹣4=3,
故选:C.
5.解:设△ABC的面积为S,边BC上的高为h,
∵△ABC≌△DEF,BC=6,△DEF的面积为18,
∴两三角形的面积相等即S=18,
又S=?BC?h=18,
∴h=6,
故选:D.
6.解:观察图象可知△MNP≌△MFD.
故选:A.
7.解:∵∠CDB′=94°,
∴∠ADB=∠CDB′=94°,
∴∠BAD=180°﹣∠B﹣∠ADB=60°,
∵AB′平分∠BAC,
∴∠BAC=2∠BAD=120°,
∴∠C=180°﹣∠B﹣∠BAC=34°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=34°,
故选:A.
8.解:∵△ABC与△DEF全等,
∴3+4+5=3+3x﹣2+2x+1,
解得:x=2,
故选:A.
二.填空题
9.解:∵△ABC≌△DEF,∠A=45°,
∴∠D=∠A=45°,
∴∠F=180°﹣∠E﹣∠F=180°﹣45°﹣60°=75°,
故答案为:75.
10.解:∵∠B=70°,∠ACB=30°,
∴∠A=180°﹣∠B﹣∠ACB=80°,
∵△ABC≌△DFE,
∴∠D=∠A=80°,
故答案为:80.
11.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB=43°,
∵∠A=45°,
∴∠ABC=180°﹣∠A﹣∠ACB=92°,
故答案为:92°.
12.解:∵△ACD≌△CBE,AD=24,BE=10,
∴CE=AD=24,CD=BE=10,
∴DE=CE﹣CD=24﹣10=14,
故答案为:14.
13.解:∵两个三角形全等,
∴x=6,y=5,
∴x﹣y=6﹣5=1,
故答案为:1.
14.解:∵△ACE≌△DBF,DA=10,CB=2,
∴AB=CD===5.
故答案为:5.
15.解:根据题意得:△AEC≌△BDA,
∴∠1+∠2=90°,
故答案为:90.
16.解:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=4,
∴BE=4,
∴AE=8﹣4=4,
∴点E的运动时间为4÷2=2(秒);
②当E在BN上,AC=BE时,
∵AC=4,
∴BE=4,
∴AE=8+4=12,
∴点E的运动时间为12÷2=6(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=8+8=16,
点E的运动时间为16÷2=8(秒),
故答案为:0,2,6,8.
三.解答题
17.解:BF=CE,
理由如下:∵△ABE≌△ACF,
∴AB=AC,AE=AF,
∴AB﹣AF=AC﹣AE,即BF=CE.
18.解:∵△ADE≌△BCF,
∴AD=BC=8cm,
∵BD=BC﹣CD,CD=5cm,
∴BD=8﹣5=3cm.
19.证明:∵△ABC≌△DEC,
∴∠B=∠DEC,BC=EC,
∴∠B=∠BEC,
∴∠BEC=∠DEC,
∴CE平分∠BED.
20.解:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
21.解:(1)∵△DEF≌△ABC,
∴BC=EF,
∵BC=6,CE=3,
∴EF=6,
∴CF=EF+EC=6+3=9;
(2)DE⊥EF,
理由:∵AB⊥BC,
∴∠ABC=90°,
∴∠ABC=∠DEF=90°,
∴DE⊥EF.
22.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
23.解:(1)∵BD⊥DE,
∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,
∴∠DBA=∠CAE
∴∠BAD+∠CAE=90°,
∴∠BAC=90°;
(2)∵△ABD≌△CAE,
∴AC=AB=4,
∴△ABC的面积=×4×4=8.
24.(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
一.选择题
1.如图,△ABC≌△ADC,则与∠BAC相等的角是( )
A.∠ACD B.∠ADC C.∠DAC D.∠ACB
2.已知图中的两个三角形全等,则∠1等于( )
A.70° B.50° C.60° D.120°
3.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED B.∠BAD=∠CAE C.AB=AE D.AC=DE
4.如图,△ABC≌△EBD,AB=4,BD=7,则CE的长度为( )
A.1 B.2 C.3 D.4
5.已知△ABC≌△DEF,且△DEF的面积为18,BC=6,则BC边上的高等于( )
A.13 B.3 C.4 D.6
6.图中的小正方形边长都相等,若△MNP≌△MFQ,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
7.如图,△ABC≌△A′B′C′,边B′C′过点A且平分∠BAC交BC于点D,∠B=26°,∠CDB′=94°,则∠C′的度数为( )
A.34° B.40° C.45° D.60°
8.已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A.2 B.2或 C.或 D.2或或
二.填空题
9.如图,已知△ABC≌△DEF且∠A=45°,∠E=60°,那么∠F= 度.
10.如图,△ABC≌△DFE,∠B=70°,∠ACB=30°,则∠D= °.
11.如图,△ABC≌△DBC,∠A=45°,∠DCB=43°,则∠ABC= .
12.如图,△ACD≌△CBE,且点D在边CE上.若AD=24,BE=10,则DE的长为 .
13.一个三角形的三边为3、5、x,另一个三角形的三边为y、3、6,若这两个三角形全等,则x﹣y= .
14.如图,△ACE≌△DBF,如果∠E=∠F,DA=12,CB=2,那么线段AB的长是 .
15.如图是由相同的小正方形组成的网格,点A,B,C均在格点上,连接AB,AC,则∠1+∠2= °.
16.如图,CA⊥AB于点A,AB=8,AC=4,射线BM⊥AB于点B,一动点E从A点出发以2个单位/秒沿射线AB运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,若点E经过t秒(t>0),△DEB与△BCA全等,则的t值为 秒.
三.解答题
17.如图,已知△ABE≌△ACF,请确定BF与CE的大小关系,并说明理由.
18.如图,△ADE≌△BCF,AD=8cm,CD=5cm,试求BD的长.
19.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
20.如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE,求证:BD=CE+DE.
21.如图,点B、C、E、F在同一直线上,AB⊥BC于点B,△DEF≌△ABC,且BC=6,CE=3.
(1)求CF的长;
(2)判断DE与EF的位置关系,并说明理由.
22.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
23.如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)求△ABC的面积.
24.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
参考答案
一.选择题
1.解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
故选:C.
2.解:∵△ABC≌△DEF,
∴∠E=∠B=70°,
∴∠1=180°﹣50°﹣70°=60°,
故选:C.
3.解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
4.解:∵△ABC≌△EBD,
∴AB=BE=4,BC=BD=7,
∴EC=BC﹣BE=7﹣4=3,
故选:C.
5.解:设△ABC的面积为S,边BC上的高为h,
∵△ABC≌△DEF,BC=6,△DEF的面积为18,
∴两三角形的面积相等即S=18,
又S=?BC?h=18,
∴h=6,
故选:D.
6.解:观察图象可知△MNP≌△MFD.
故选:A.
7.解:∵∠CDB′=94°,
∴∠ADB=∠CDB′=94°,
∴∠BAD=180°﹣∠B﹣∠ADB=60°,
∵AB′平分∠BAC,
∴∠BAC=2∠BAD=120°,
∴∠C=180°﹣∠B﹣∠BAC=34°,
∵△ABC≌△A′B′C′,
∴∠C′=∠C=34°,
故选:A.
8.解:∵△ABC与△DEF全等,
∴3+4+5=3+3x﹣2+2x+1,
解得:x=2,
故选:A.
二.填空题
9.解:∵△ABC≌△DEF,∠A=45°,
∴∠D=∠A=45°,
∴∠F=180°﹣∠E﹣∠F=180°﹣45°﹣60°=75°,
故答案为:75.
10.解:∵∠B=70°,∠ACB=30°,
∴∠A=180°﹣∠B﹣∠ACB=80°,
∵△ABC≌△DFE,
∴∠D=∠A=80°,
故答案为:80.
11.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB=43°,
∵∠A=45°,
∴∠ABC=180°﹣∠A﹣∠ACB=92°,
故答案为:92°.
12.解:∵△ACD≌△CBE,AD=24,BE=10,
∴CE=AD=24,CD=BE=10,
∴DE=CE﹣CD=24﹣10=14,
故答案为:14.
13.解:∵两个三角形全等,
∴x=6,y=5,
∴x﹣y=6﹣5=1,
故答案为:1.
14.解:∵△ACE≌△DBF,DA=10,CB=2,
∴AB=CD===5.
故答案为:5.
15.解:根据题意得:△AEC≌△BDA,
∴∠1+∠2=90°,
故答案为:90.
16.解:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=4,
∴BE=4,
∴AE=8﹣4=4,
∴点E的运动时间为4÷2=2(秒);
②当E在BN上,AC=BE时,
∵AC=4,
∴BE=4,
∴AE=8+4=12,
∴点E的运动时间为12÷2=6(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=8+8=16,
点E的运动时间为16÷2=8(秒),
故答案为:0,2,6,8.
三.解答题
17.解:BF=CE,
理由如下:∵△ABE≌△ACF,
∴AB=AC,AE=AF,
∴AB﹣AF=AC﹣AE,即BF=CE.
18.解:∵△ADE≌△BCF,
∴AD=BC=8cm,
∵BD=BC﹣CD,CD=5cm,
∴BD=8﹣5=3cm.
19.证明:∵△ABC≌△DEC,
∴∠B=∠DEC,BC=EC,
∴∠B=∠BEC,
∴∠BEC=∠DEC,
∴CE平分∠BED.
20.解:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
21.解:(1)∵△DEF≌△ABC,
∴BC=EF,
∵BC=6,CE=3,
∴EF=6,
∴CF=EF+EC=6+3=9;
(2)DE⊥EF,
理由:∵AB⊥BC,
∴∠ABC=90°,
∴∠ABC=∠DEF=90°,
∴DE⊥EF.
22.解:(1)∵△ABC≌△DEB,DE=10,BC=4,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
23.解:(1)∵BD⊥DE,
∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,
∴∠DBA=∠CAE
∴∠BAD+∠CAE=90°,
∴∠BAC=90°;
(2)∵△ABD≌△CAE,
∴AC=AB=4,
∴△ABC的面积=×4×4=8.
24.(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
