人教版2021年八年级数学上册:12.1《全等三角形》课时练习(word版,含解析)
文档属性
| 名称 | 人教版2021年八年级数学上册:12.1《全等三角形》课时练习(word版,含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 147.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 17:28:55 | ||
图片预览

文档简介
人教版2021年八年级数学上册:12.1《全等三角形》课时练习
一.选择题
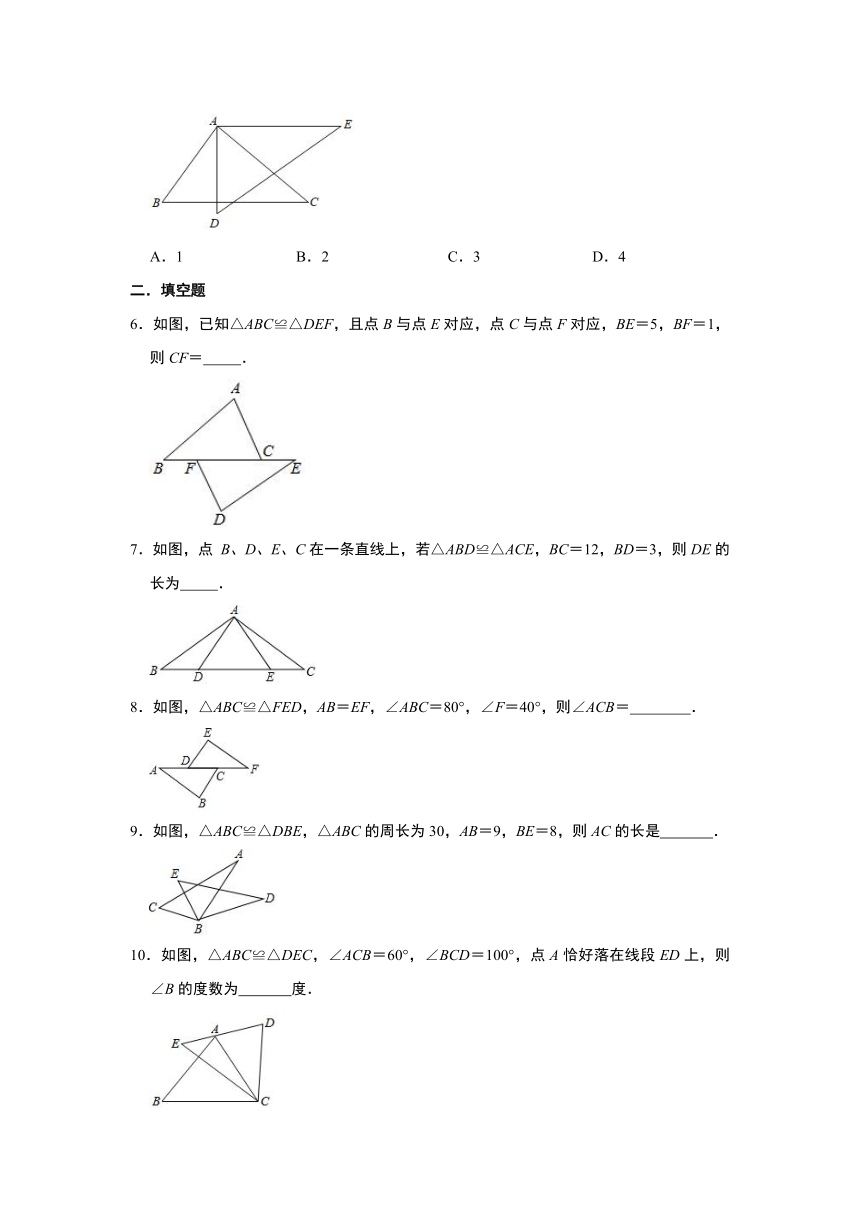
1.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠BAD=∠CAE B.AC=DE C.∠ABC=∠AED D.AB=AE
2.图中的两个三角形全等,则∠1等于( )
A.45° B.62° C.73° D.135°
3.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2 B.3 C.5 D.7
4.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
5.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1 B.2 C.3 D.4
二.填空题
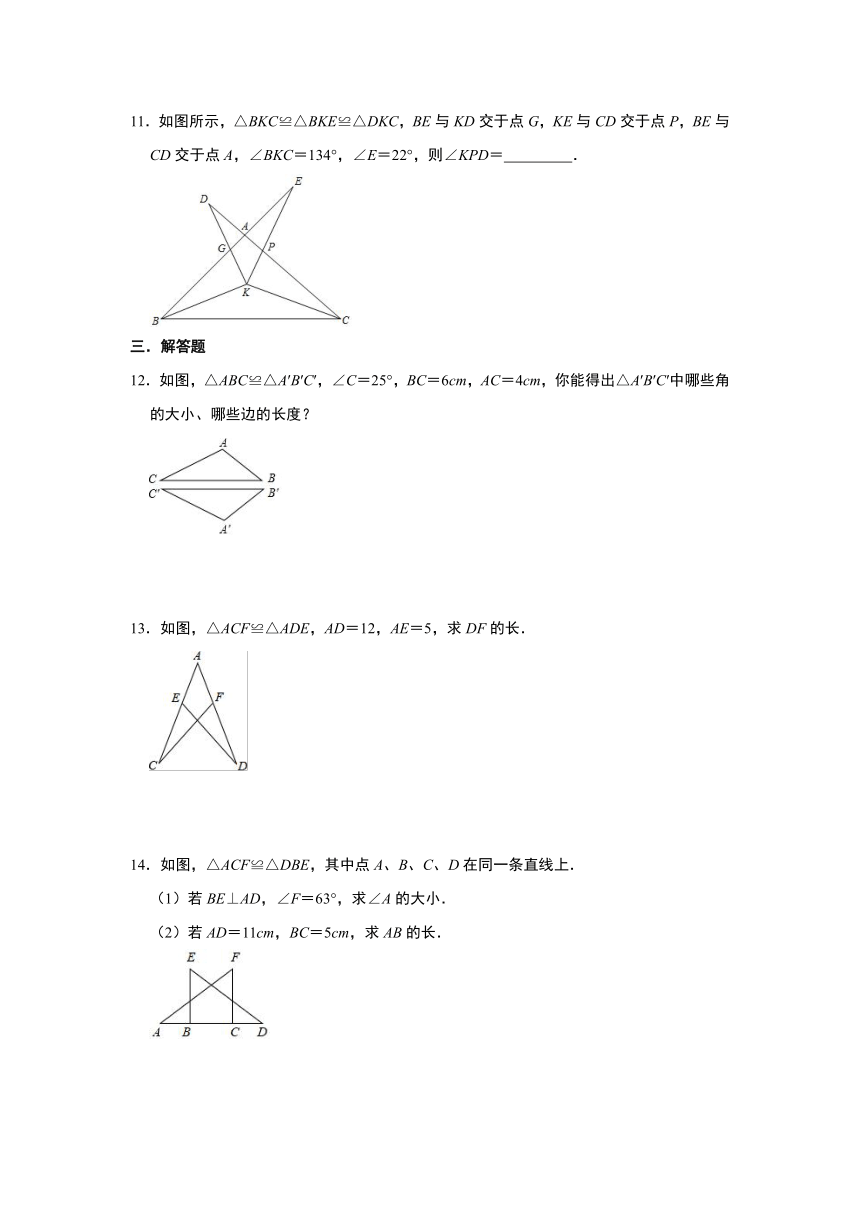
6.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF= .
7.如图,点 B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为 .
8.如图,△ABC≌△FED,AB=EF,∠ABC=80°,∠F=40°,则∠ACB= .
9.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
10.如图,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为 度.
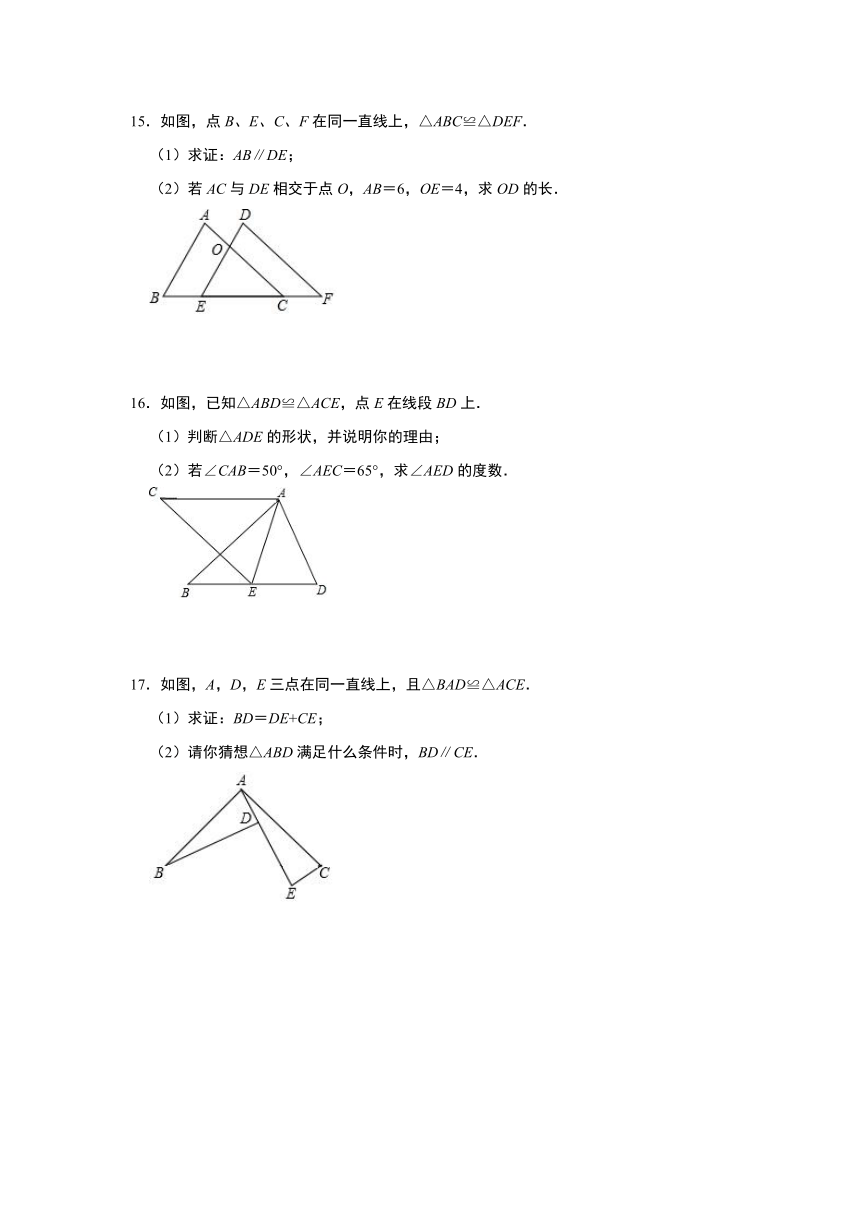
11.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD= .
三.解答题
12.如图,△ABC≌△A′B′C′,∠C=25°,BC=6cm,AC=4cm,你能得出△A′B′C′中哪些角的大小、哪些边的长度?
13.如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
14.如图,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小.
(2)若AD=11cm,BC=5cm,求AB的长.
15.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
16.如图,已知△ABD≌△ACE,点E在线段BD上.
(1)判断△ADE的形状,并说明你的理由;
(2)若∠CAB=50°,∠AEC=65°,求∠AED的度数.
17.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
参考答案
一.选择题
1.解:A、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAD﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,本选项结论成立;
B、∵△ABC≌△ADE,
∴AC=AE,而AC与DE不一定相等,本选项结论不成立;
C、∵△ABC≌△ADE,
∴∠C=∠AED,而∠ABC与∠AED不一定相等,本选项结论不成立;
D、∵△ABC≌△ADE,
∴AB=AD,而AB与AE不一定相等,本选项结论不成立;
故选:A.
2.解:∵两个三角形全等,
∴边长为a的对角是对应角,
∴∠1=73°,
故选:C.
3.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
4.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
5.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
二.填空题
6.解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
7.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
8.解:∵△ABC≌△FED,∠ABC=80°,∠F=40°,
∴∠ABC=∠FED=80°,∠A=∠F=40°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣40°﹣80°=60°,
故答案为:60°.
9.解:∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30﹣AB﹣BC=13,
故答案为:13.
10.解:∵△ABC≌△DEC,
∴∠DCE=∠ACB=60°,AC=CD,∠D=∠BAC,
∴∠D=∠DAC,
∵∠BCD=100°,∠ACB=60°,
∴∠ACD=∠BCD﹣∠ACB=100°﹣60°=40°,
∴∠BAC=∠D=×(180°﹣40°)=70°,
∴∠B=180°﹣∠ACB﹣∠BAC=180°﹣70°﹣60°=50°,
故答案为:50.
11.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
三.解答题
12.解:∵△ABC≌△A′B′C′,
∴∠C′=∠C=25°,B′C′=BC=6cm,A′C′=4cm,
故能得出△A′B′C′中∠C′的大小,边B′C′,A′C′长度.
13.解:∵△ACF≌△ADE,AD=12,AE=5,
∴AC=AD=12,AE=AF=5,
∴DF=12﹣5=7.
14.解:(1)∵BE⊥AD,
∴∠EBD=90°,
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°﹣∠F=27°;
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA﹣CB=BD﹣BC,即AB=CD,
∵AD=11cm,BC=5cm,
∴AB+CD=11﹣5=6cm,
∴AB=3cm.
15.(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE;
(2)解:∵△ABC≌△DEF,
∴AB=DE=6,
∵OE=4,
∴OD=DE﹣OE=6﹣4=2.
16.解:(1)△ADE是等腰三角形,
理由是:∵△ABD≌△ACE,
∴AD=AE,
∴△ADE是等腰三角形;
(2)∵△ABD≌△ACE,
∴∠D=∠AEC,AD=AE,
∴∠AED=∠D,
∴∠AED=∠AEC,
∵∠AEC=65°,
∴∠AED=65°.
17.(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:若BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
一.选择题
1.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠BAD=∠CAE B.AC=DE C.∠ABC=∠AED D.AB=AE
2.图中的两个三角形全等,则∠1等于( )
A.45° B.62° C.73° D.135°
3.如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2 B.3 C.5 D.7
4.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
5.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1 B.2 C.3 D.4
二.填空题
6.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF= .
7.如图,点 B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为 .
8.如图,△ABC≌△FED,AB=EF,∠ABC=80°,∠F=40°,则∠ACB= .
9.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
10.如图,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为 度.
11.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD= .
三.解答题
12.如图,△ABC≌△A′B′C′,∠C=25°,BC=6cm,AC=4cm,你能得出△A′B′C′中哪些角的大小、哪些边的长度?
13.如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
14.如图,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小.
(2)若AD=11cm,BC=5cm,求AB的长.
15.如图,点B、E、C、F在同一直线上,△ABC≌△DEF.
(1)求证:AB∥DE;
(2)若AC与DE相交于点O,AB=6,OE=4,求OD的长.
16.如图,已知△ABD≌△ACE,点E在线段BD上.
(1)判断△ADE的形状,并说明你的理由;
(2)若∠CAB=50°,∠AEC=65°,求∠AED的度数.
17.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
参考答案
一.选择题
1.解:A、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAD﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,本选项结论成立;
B、∵△ABC≌△ADE,
∴AC=AE,而AC与DE不一定相等,本选项结论不成立;
C、∵△ABC≌△ADE,
∴∠C=∠AED,而∠ABC与∠AED不一定相等,本选项结论不成立;
D、∵△ABC≌△ADE,
∴AB=AD,而AB与AE不一定相等,本选项结论不成立;
故选:A.
2.解:∵两个三角形全等,
∴边长为a的对角是对应角,
∴∠1=73°,
故选:C.
3.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
4.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
5.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
二.填空题
6.解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
7.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
8.解:∵△ABC≌△FED,∠ABC=80°,∠F=40°,
∴∠ABC=∠FED=80°,∠A=∠F=40°,
∵∠A+∠ABC+∠ACB=180°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣40°﹣80°=60°,
故答案为:60°.
9.解:∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30﹣AB﹣BC=13,
故答案为:13.
10.解:∵△ABC≌△DEC,
∴∠DCE=∠ACB=60°,AC=CD,∠D=∠BAC,
∴∠D=∠DAC,
∵∠BCD=100°,∠ACB=60°,
∴∠ACD=∠BCD﹣∠ACB=100°﹣60°=40°,
∴∠BAC=∠D=×(180°﹣40°)=70°,
∴∠B=180°﹣∠ACB﹣∠BAC=180°﹣70°﹣60°=50°,
故答案为:50.
11.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
三.解答题
12.解:∵△ABC≌△A′B′C′,
∴∠C′=∠C=25°,B′C′=BC=6cm,A′C′=4cm,
故能得出△A′B′C′中∠C′的大小,边B′C′,A′C′长度.
13.解:∵△ACF≌△ADE,AD=12,AE=5,
∴AC=AD=12,AE=AF=5,
∴DF=12﹣5=7.
14.解:(1)∵BE⊥AD,
∴∠EBD=90°,
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°﹣∠F=27°;
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA﹣CB=BD﹣BC,即AB=CD,
∵AD=11cm,BC=5cm,
∴AB+CD=11﹣5=6cm,
∴AB=3cm.
15.(1)证明:∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE;
(2)解:∵△ABC≌△DEF,
∴AB=DE=6,
∵OE=4,
∴OD=DE﹣OE=6﹣4=2.
16.解:(1)△ADE是等腰三角形,
理由是:∵△ABD≌△ACE,
∴AD=AE,
∴△ADE是等腰三角形;
(2)∵△ABD≌△ACE,
∴∠D=∠AEC,AD=AE,
∴∠AED=∠D,
∴∠AED=∠AEC,
∵∠AEC=65°,
∴∠AED=65°.
17.(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:若BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
