人教版八上高分笔记之导与练 12.1 全等三角形(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 12.1 全等三角形(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 19:35:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
全等三角形
12.1全等三角形
知识要点:
能够
?的两个图形叫做全等形.
2.能够?
?的两个三角形叫做全等三角形,“全等”用符号“_
_?”表示,读作“?
?“
3.全等三角形的对应边?
?,对应角?
4.经过?
、
、
等变换前后的两个三角形全等.
易错点睛:
如图,ΔABC≌△ACD,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的序号有?
?
【点睛】??没抓住二符号确定对应边与对应角而出错。
典例讲解:
题型一
利用全等三角形的性质进行有关线段的计算或证明
?如图,A,D,E三点在一条直线上,且ΔBAD≌ΔACE.求证:BD=CE+DE.?
变式练习:
「教材P33习题12.1T4变式题]如图,ΔACE≌ΔDBF,AC=6,BC=4.求AD的长.
2、如图,ΔACF≌ΔDBE,AD=11,BC=7.(1)求证:AB=CD;(2)求AB的长.
题型二
利用全等三角形的性质进行有关角的计算或证明
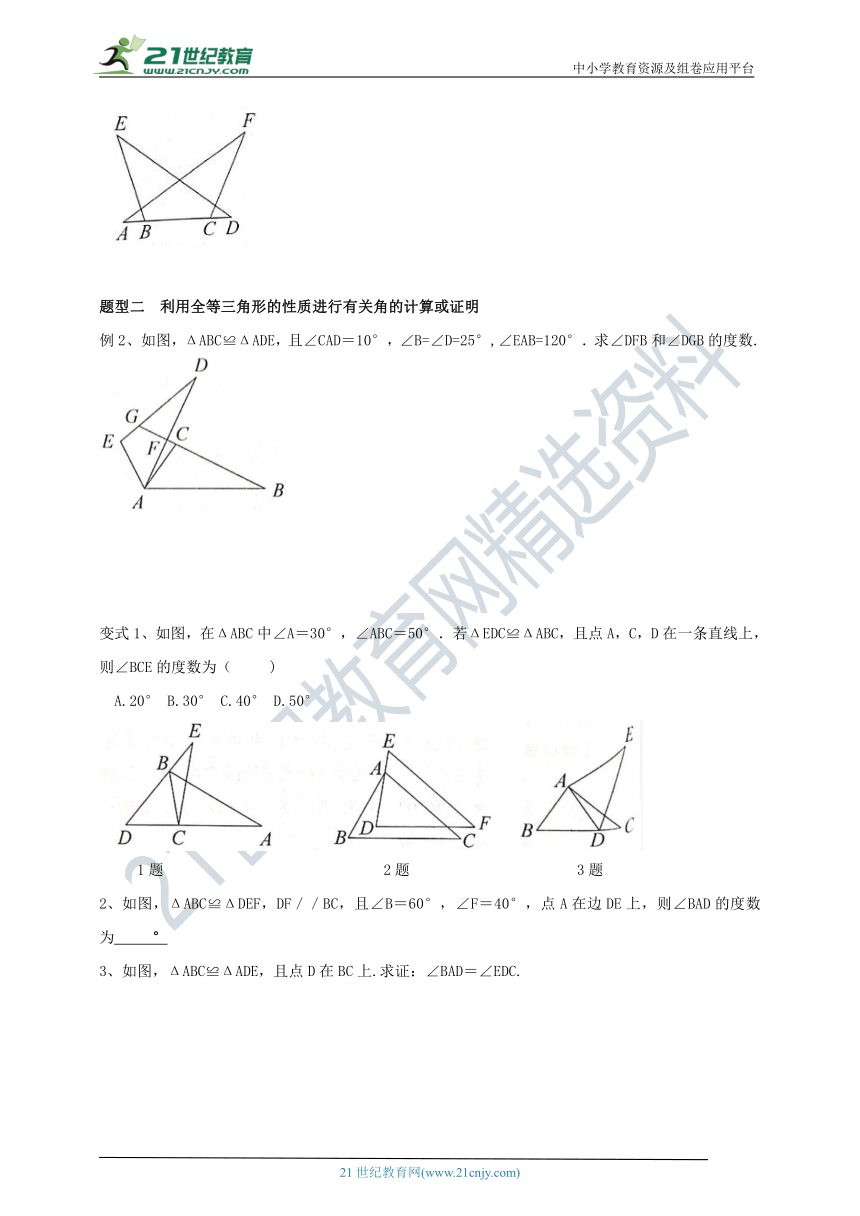
如图,ΔABC≌ΔADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
变式1、如图,在ΔABC中∠A=30°,∠ABC=50°.若ΔEDC≌ΔABC,且点A,C,D在一条直线上,则∠BCE的度数为(
?)
A.20°
B.30°
C.40°
D.50°
1题
2题
3题
如图,ΔABC≌ΔDEF,DF//BC,且∠B=60°,∠F=40°,点A在边DE上,则∠BAD的度数为??
°
3、如图,ΔABC≌ΔADE,且点D在BC上.求证:∠BAD=∠EDC.
题型三
利用全等三角形的性质判断两直线的位置关系
如图,ΔACE≌ΔDBF,点A,B,C,D在一条直线上.AE与DF平行吗?EC与BF呢?请说明理由.
解题策略:证明两直线平行,常通过同位角相等、内错角相等、同旁内角互补或平行于同一线的两直线平行证得.具体采用哪种方法要根据已知条件进行灵活选取.
如图,点A,B,C在一条直线上,点E在BD上,且ΔABD≌ΔEBC.
(1)判断AC与BD的位置关系,并说明理由;
(2)判断直线AD与直线CE的位置关系,并说明理由.
解题策略:证明两直线垂直可转化为证明它们的夹角为90°.当题目中没有给出任何角的度数时,常常借助两个等角的和是180°来证明.
变式练习:
如图,点A,B,C,D在一条直线上,点E,F是直线AD上方的点,连接AE,CE,BF,DF,若ΔACE≌ΔFDB,FD=3,AD=8.
(1)直线CE与DF是否平行?说明理由;
(2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
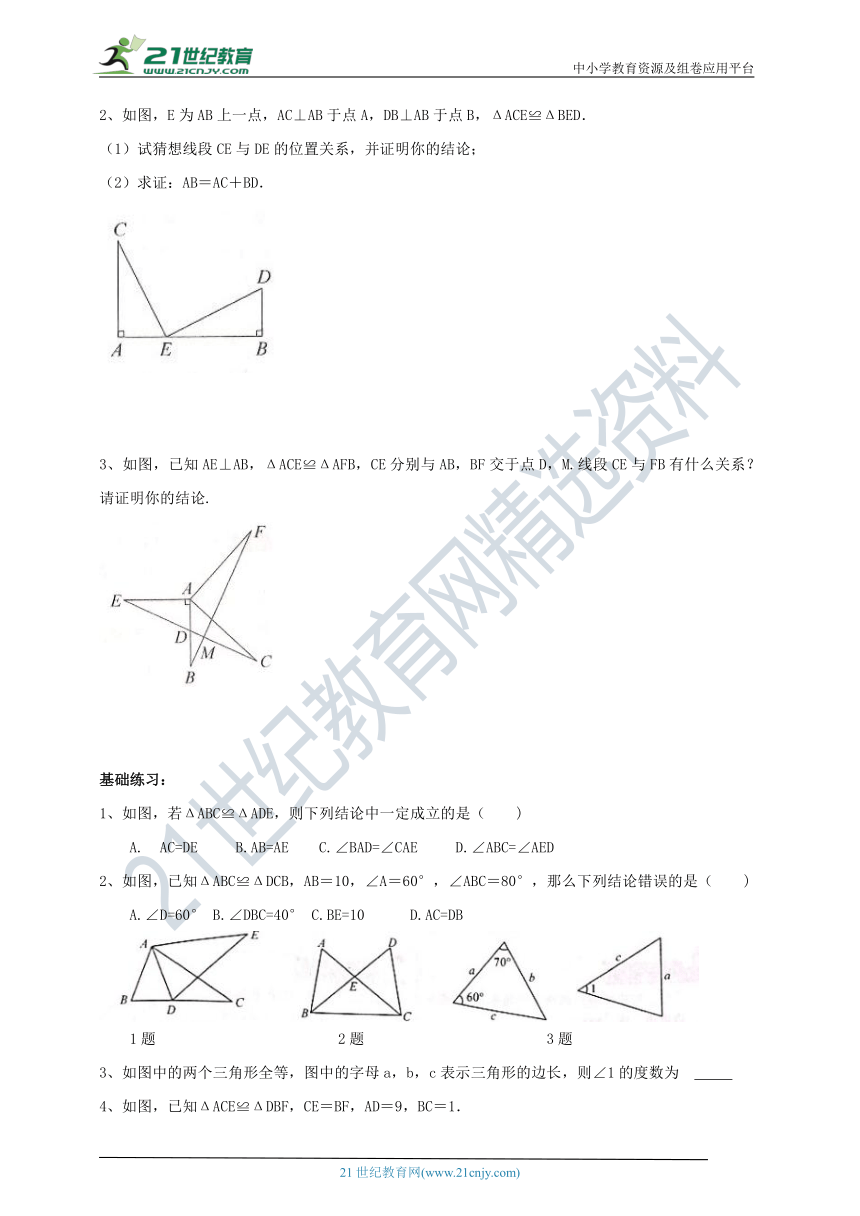
2、如图,E为AB上一点,AC⊥AB于点A,DB⊥AB于点B,ΔACE≌ΔBED.
(1)试猜想线段CE与DE的位置关系,并证明你的结论;
(2)求证:AB=AC+BD.
3、如图,已知AE⊥AB,ΔACE≌ΔAFB,CE分别与AB,BF交于点D,M.线段CE与FB有什么关系?请证明你的结论.
基础练习:
如图,若ΔABC≌ΔADE,则下列结论中一定成立的是(?
)
AC=DE
B.AB=AE
C.∠BAD=∠CAE
D.∠ABC=∠AED
2、如图,已知ΔABC≌ΔDCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论错误的是(?
)
A.∠D=60°
B.∠DBC=40°
C.BE=10
D.AC=DB
1题
2题
3题
3、如图中的两个三角形全等,图中的字母a,b,c表示三角形的边长,则∠1的度数为??
4、如图,已知ΔACE≌ΔDBF,CE=BF,AD=9,BC=1.
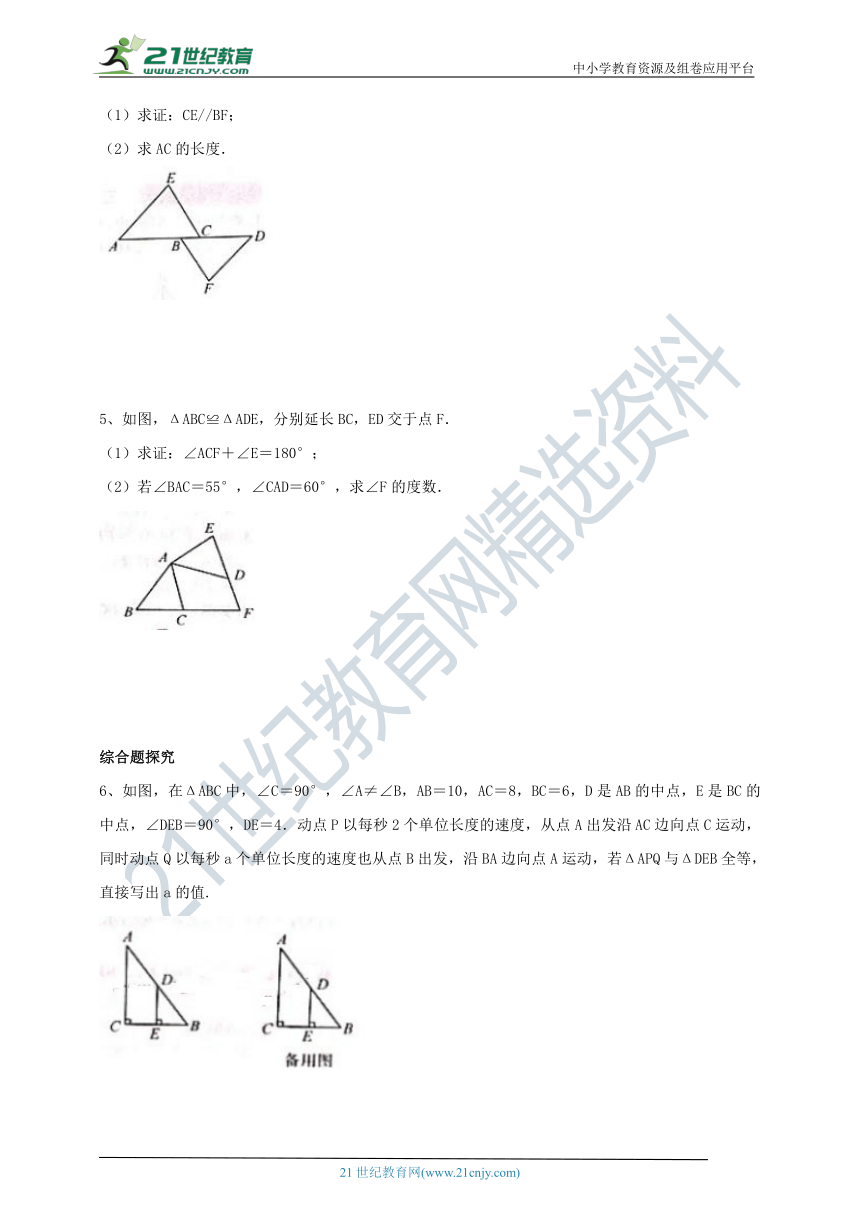
(1)求证:CE//BF;
(2)求AC的长度.
5、如图,ΔABC≌ΔADE,分别延长BC,ED交于点F.
(1)求证:∠ACF+∠E=180°;
(2)若∠BAC=55°,∠CAD=60°,求∠F的度数.
综合题探究
6、如图,在ΔABC中,∠C=90°,∠A≠∠B,AB=10,AC=8,BC=6,D是AB的中点,E是BC的中点,∠DEB=90°,DE=4.动点P以每秒2个单位长度的速度,从点A出发沿AC边向点C运动,同时动点Q以每秒a个单位长度的速度也从点B出发,沿BA边向点A运动,若ΔAPQ与ΔDEB全等,直接写出a的值.
答案:
知识要点:
1.能够
完全重合?的两个图形叫做全等形.
2.能够?完全重合?的两个三角形叫做全等三角形,“全等”用符号“_≌_?”表示,读作“?全等于??“
3.全等三角形的对应边?相等?,对应角?相等
4.经过?平移?、翻折、旋转
等变换前后的两个三角形全等.
易错点睛:
如图,ΔABC≌△ACD,下列结论:①AB与AD是对应边;②AC与CA是对应
边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的序号有??②④
【点睛】??没抓住二符号确定对应边与对应角而出错。
典例讲解:
题型一
利用全等三角形的性质进行有关线段的计算或证明
?如图,A,D,E三点在一条直线上,且ΔBAD≌ΔACE.求证:BD=CE+DE.?
证明:∵ΔBAD≌ΔACE,∴BD=AE,AD=CE.
∵AE=AD+DE,∴BD=AD+DE=CE+DE.
由两个三角形全等得到线段相等,再将其中一条较长的线段转化为两条线段的和,最后通过等量代换得出结论.
变式练习:
「教材P33习题12.1T4变式题]如图,ΔACE≌ΔDBF,AC=6,BC=4.求AD的长.
解:∵ΔACE≌ΔDBF,?∴AC=DB=6.?
∴CD=DB-BC=6-4=2.?
∴AD=AC+CD=6+2=8.
2、如图,ΔACF≌ΔDBE,AD=11,BC=7.
(1)求证:AB=CD;(2)求AB的长.
(1)证明:∵ΔACF≌ΔDBE,∴AC=DB.?
∴AC-BC=DB-BC,即AB=CD.?
(2)解:∵AD=11,BC=7,AB=CDAB=(AD-BC)=2
题型二
利用全等三角形的性质进行有关角的计算或证明
如图,ΔABC≌ΔADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
解:∵ΔABC≌ΔADE,∠CAD=10°,∠EAB=120°
∴∠BAC=∠DAE=(∠EAB-∠CAD)=(120°-10°)=55°.?
∵∠B=25°,∴∠DFB=∠FAB+∠B=∠CAD+?∠BAC+∠B=10°+55°+25°=90°
∵∠D=25°,?
∴∠DGB=∠DFB-∠D=90°-25°=65°.?
变式1、如图,在ΔABC中∠A=30°,∠ABC=50°.若ΔEDC≌ΔABC,且点A,C,D在一条直线上,则∠BCE的度数为(
A?)
A.20°
B.30°
C.40°
D.50°
1题
2题
3题
2、如图,ΔABC≌ΔDEF,DF//BC,且∠B=60°,∠F=40°,点A在边DE上,则∠BAD的度数为??20°
3、如图,ΔABC≌ΔADE,且点D在BC上.求证:∠BAD=∠EDC.
证明:∵ΔABC≌ΔADE,
∴∠B=∠ADE.??????????
∵∠ADC=∠B+∠BAD=∠ADE+∠EDC,???????????
∴∠BAD=∠EDC.?
题型三
利用全等三角形的性质判断两直线的位置关系
如图,ΔACE≌ΔDBF,点A,B,C,D在一条直线上.AE与DF平行吗?EC与BF呢?请说明理由.
解:AE//DF,EC//BF.理由如下:
∵ΔACE≌ΔDBF,∴∠A=∠D,∠ECA=∠FBD.?
∴AE//DF,EC//BF.?
解题策略:证明两直线平行,常通过同位角相等、内错角相等、同旁内角互补或平行于同一线的两直线平行证得.具体采用哪种方法要根据已知条件进行灵活选取.
如图,点A,B,C在一条直线上,点E在BD上,且ΔABD≌ΔEBC.
(1)判断AC与BD的位置关系,并说明理由;
(2)判断直线AD与直线CE的位置关系,并说明理由.
解:(1)AC⊥BD.理由如下:
∵ΔABD≌ΔEBC,∵∠ABD=∠EBC.
∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°(平角等于180°).
∴∠ABD=∠EBC=90°,∴AC⊥BD.
(2)直线AD⊥直线CE.理由如下:
如图,延长CE交AD于点F.
∵ΔABD≌ΔEBC,
∴∠D=∠C.
在RtΔABD中.∴∠A+∠D=90°,
∠A+∠C=90°∴∠DFC=∠A+∠C=90°,
直线AD⊥直线CE.
解题策略:证明两直线垂直可转化为证明它们的夹角为90°.当题目中没有给出任何角的度数时,常常借助两个等角的和是180°来证明.
变式练习:
如图,点A,B,C,D在一条直线上,点E,F是直线AD上方的点,连接AE,CE,BF,DF,若ΔACE≌ΔFDB,FD=3,AD=8.
(1)直线CE与DF是否平行?说明理由;
(2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
解:(1)CE//DF.?
理由:∵ΔACE≌ΔFDB,
∴∠ACE=∠D,?
∴CE//DF.
(2)ΔACE≌ΔFDB,?
∴AC=FD=3.?
∵AD=8,∴CD=AD-AC=8-3=5.?
(3)∵ΔACE≌ΔFDB,∴∠A=∠F=53°.?
∴∠ACE=180°-∠A-∠E=180°-53°-?26°=101°.
2、如图,E为AB上一点,AC⊥AB于点A,DB⊥AB于点B,ΔACE≌ΔBED.
(1)试猜想线段CE与DE的位置关系,并证明你的结论;
(2)求证:AB=AC+BD.
(1)解:CE⊥DE.
证明如下:???????
∵AC⊥AB,?
∴∠A=90°.????????????
∴∠C+∠CEA=90°.?
∵ΔACE≌ΔBED,??
∴∠C=∠DEB.?
∴∠DEB+∠CEA=90°.?
∴∠CED=180°-∠DEB-∠CEA=180°-?90°=90°∴CE⊥DE.
(2)证明:∵ΔACE≌ΔBED,
∴AC=BE,AE=BD.
∴AB=BE+AE=AC+BD.
3、如图,已知AE⊥AB,ΔACE≌ΔAFB,CE分别与AB,BF交于点D,M.线段CE与FB有什么关系?请证明你的结论.
解:CE=FB,且?CE⊥FB.
证明如下:
AE⊥AB,
∵∠BAE=90°.
∴∠E+∠ADE=90°.
∵ΔACE≌ΔAFB,∴∠E=∠B,CE=FB.?
又∵∠ADE=∠BDM,
∴∠E+∠ADE=∠B+∠BDM=90°.
∴∠BMD=180°-∠B-∠BDM=90°.
∴CE⊥FB.?
基础练习:
如图,若ΔABC≌ΔADE,则下列结论中一定成立的是(?C)
AC=DE
B.AB=AE
C.∠BAD=∠CAE
D.∠ABC=∠AED
2、如图,已知ΔABC≌ΔDCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论错误的是(?C)
A.∠D=60°
B.∠DBC=40°
C.BE=10
D.AC=DB
1题
2题
3题
如图中的两个三角形全等,图中的字母a,b,c表示三角形的边长,则∠1的度数为??50°
4、如图,已知ΔACE≌ΔDBF,CE=BF,AD=9,BC=1.
(1)求证:CE//BF;
(2)求AC的长度.
解:(1)证明:∵ΔACE≌ΔDBF,∴∠ACE=∠DBF,∴CE//BF;
(2)∵ΔACE≌ΔDBF,∴AC=BD,AC-BC=BD-BC,?
∴AB=CD=(AD-BC)÷2=4,∴AC=AB+BC=4+1=5.?
5、如图,ΔABC≌ΔADE,分别延长BC,ED交于点F.
(1)求证:∠ACF+∠E=180°;
(2)若∠BAC=55°,∠CAD=60°,求∠F的度数.
解:(1)证明:∵ΔABC≌ΔADE,∴∠E=∠ACB.
∵∠ACF+∠ACB=180°,∴∠ACF+∠E=180°;?
(2)∵ΔABC≌ΔADE,∴∠EAD≌∠BAC=55°.∵∠CAD=60°,?
∴∠CAE=∠CAD+∠EAD=115°.?
∵∠ACF+∠E+∠CAE+∠F=360°,∠ACF+∠E=180°,?
∴180°+115°+∠F=360°∴∠F=65°.?
综合题探究
6、如图,在ΔABC中,∠C=90°,∠A≠∠B,AB=10,AC=8,BC=6,D是AB的中点,E是BC的中点,∠DEB=90°,DE=4.动点P以每秒2个单位长度的速度,从点A出发沿AC边向点C运动,同时动点Q以每秒a个单位长度的速度也从点B出发,沿BA边向点A运动,若ΔAPQ与ΔDEB全等,直接写出a的值.
解:a的值为2.4或2.5.设运动时间为ts,则AP=2t,BQ=at,AQ=10-at.
∵∠C=∠DEB=90°,∴AC//DE,
∴∠A=∠EDB≠∠B.
若ΔAPQ≌ΔDEB,
∴AP=DE=4,AQ=DB=5,
∴2t=4,10-at=5,∴t=2,a=2.5;
若ΔAQP≌ΔDEB.
∴AP=DB=5,AQ=DE=4,∴2t=5,10-at=4,∴t=2.5,a=2.4;
综上所述,a的值为2.4或2.5
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
全等三角形
12.1全等三角形
知识要点:
能够
?的两个图形叫做全等形.
2.能够?
?的两个三角形叫做全等三角形,“全等”用符号“_
_?”表示,读作“?
?“
3.全等三角形的对应边?
?,对应角?
4.经过?
、
、
等变换前后的两个三角形全等.
易错点睛:
如图,ΔABC≌△ACD,下列结论:①AB与AD是对应边;②AC与CA是对应边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的序号有?
?
【点睛】??没抓住二符号确定对应边与对应角而出错。
典例讲解:
题型一
利用全等三角形的性质进行有关线段的计算或证明
?如图,A,D,E三点在一条直线上,且ΔBAD≌ΔACE.求证:BD=CE+DE.?
变式练习:
「教材P33习题12.1T4变式题]如图,ΔACE≌ΔDBF,AC=6,BC=4.求AD的长.
2、如图,ΔACF≌ΔDBE,AD=11,BC=7.(1)求证:AB=CD;(2)求AB的长.
题型二
利用全等三角形的性质进行有关角的计算或证明
如图,ΔABC≌ΔADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
变式1、如图,在ΔABC中∠A=30°,∠ABC=50°.若ΔEDC≌ΔABC,且点A,C,D在一条直线上,则∠BCE的度数为(
?)
A.20°
B.30°
C.40°
D.50°
1题
2题
3题
如图,ΔABC≌ΔDEF,DF//BC,且∠B=60°,∠F=40°,点A在边DE上,则∠BAD的度数为??
°
3、如图,ΔABC≌ΔADE,且点D在BC上.求证:∠BAD=∠EDC.
题型三
利用全等三角形的性质判断两直线的位置关系
如图,ΔACE≌ΔDBF,点A,B,C,D在一条直线上.AE与DF平行吗?EC与BF呢?请说明理由.
解题策略:证明两直线平行,常通过同位角相等、内错角相等、同旁内角互补或平行于同一线的两直线平行证得.具体采用哪种方法要根据已知条件进行灵活选取.
如图,点A,B,C在一条直线上,点E在BD上,且ΔABD≌ΔEBC.
(1)判断AC与BD的位置关系,并说明理由;
(2)判断直线AD与直线CE的位置关系,并说明理由.
解题策略:证明两直线垂直可转化为证明它们的夹角为90°.当题目中没有给出任何角的度数时,常常借助两个等角的和是180°来证明.
变式练习:
如图,点A,B,C,D在一条直线上,点E,F是直线AD上方的点,连接AE,CE,BF,DF,若ΔACE≌ΔFDB,FD=3,AD=8.
(1)直线CE与DF是否平行?说明理由;
(2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
2、如图,E为AB上一点,AC⊥AB于点A,DB⊥AB于点B,ΔACE≌ΔBED.
(1)试猜想线段CE与DE的位置关系,并证明你的结论;
(2)求证:AB=AC+BD.
3、如图,已知AE⊥AB,ΔACE≌ΔAFB,CE分别与AB,BF交于点D,M.线段CE与FB有什么关系?请证明你的结论.
基础练习:
如图,若ΔABC≌ΔADE,则下列结论中一定成立的是(?
)
AC=DE
B.AB=AE
C.∠BAD=∠CAE
D.∠ABC=∠AED
2、如图,已知ΔABC≌ΔDCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论错误的是(?
)
A.∠D=60°
B.∠DBC=40°
C.BE=10
D.AC=DB
1题
2题
3题
3、如图中的两个三角形全等,图中的字母a,b,c表示三角形的边长,则∠1的度数为??
4、如图,已知ΔACE≌ΔDBF,CE=BF,AD=9,BC=1.
(1)求证:CE//BF;
(2)求AC的长度.
5、如图,ΔABC≌ΔADE,分别延长BC,ED交于点F.
(1)求证:∠ACF+∠E=180°;
(2)若∠BAC=55°,∠CAD=60°,求∠F的度数.
综合题探究
6、如图,在ΔABC中,∠C=90°,∠A≠∠B,AB=10,AC=8,BC=6,D是AB的中点,E是BC的中点,∠DEB=90°,DE=4.动点P以每秒2个单位长度的速度,从点A出发沿AC边向点C运动,同时动点Q以每秒a个单位长度的速度也从点B出发,沿BA边向点A运动,若ΔAPQ与ΔDEB全等,直接写出a的值.
答案:
知识要点:
1.能够
完全重合?的两个图形叫做全等形.
2.能够?完全重合?的两个三角形叫做全等三角形,“全等”用符号“_≌_?”表示,读作“?全等于??“
3.全等三角形的对应边?相等?,对应角?相等
4.经过?平移?、翻折、旋转
等变换前后的两个三角形全等.
易错点睛:
如图,ΔABC≌△ACD,下列结论:①AB与AD是对应边;②AC与CA是对应
边;③∠DAC与∠BAC是对应角;④∠ACD与∠CAB是对应角.其中结论正确的序号有??②④
【点睛】??没抓住二符号确定对应边与对应角而出错。
典例讲解:
题型一
利用全等三角形的性质进行有关线段的计算或证明
?如图,A,D,E三点在一条直线上,且ΔBAD≌ΔACE.求证:BD=CE+DE.?
证明:∵ΔBAD≌ΔACE,∴BD=AE,AD=CE.
∵AE=AD+DE,∴BD=AD+DE=CE+DE.
由两个三角形全等得到线段相等,再将其中一条较长的线段转化为两条线段的和,最后通过等量代换得出结论.
变式练习:
「教材P33习题12.1T4变式题]如图,ΔACE≌ΔDBF,AC=6,BC=4.求AD的长.
解:∵ΔACE≌ΔDBF,?∴AC=DB=6.?
∴CD=DB-BC=6-4=2.?
∴AD=AC+CD=6+2=8.
2、如图,ΔACF≌ΔDBE,AD=11,BC=7.
(1)求证:AB=CD;(2)求AB的长.
(1)证明:∵ΔACF≌ΔDBE,∴AC=DB.?
∴AC-BC=DB-BC,即AB=CD.?
(2)解:∵AD=11,BC=7,AB=CDAB=(AD-BC)=2
题型二
利用全等三角形的性质进行有关角的计算或证明
如图,ΔABC≌ΔADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
解:∵ΔABC≌ΔADE,∠CAD=10°,∠EAB=120°
∴∠BAC=∠DAE=(∠EAB-∠CAD)=(120°-10°)=55°.?
∵∠B=25°,∴∠DFB=∠FAB+∠B=∠CAD+?∠BAC+∠B=10°+55°+25°=90°
∵∠D=25°,?
∴∠DGB=∠DFB-∠D=90°-25°=65°.?
变式1、如图,在ΔABC中∠A=30°,∠ABC=50°.若ΔEDC≌ΔABC,且点A,C,D在一条直线上,则∠BCE的度数为(
A?)
A.20°
B.30°
C.40°
D.50°
1题
2题
3题
2、如图,ΔABC≌ΔDEF,DF//BC,且∠B=60°,∠F=40°,点A在边DE上,则∠BAD的度数为??20°
3、如图,ΔABC≌ΔADE,且点D在BC上.求证:∠BAD=∠EDC.
证明:∵ΔABC≌ΔADE,
∴∠B=∠ADE.??????????
∵∠ADC=∠B+∠BAD=∠ADE+∠EDC,???????????
∴∠BAD=∠EDC.?
题型三
利用全等三角形的性质判断两直线的位置关系
如图,ΔACE≌ΔDBF,点A,B,C,D在一条直线上.AE与DF平行吗?EC与BF呢?请说明理由.
解:AE//DF,EC//BF.理由如下:
∵ΔACE≌ΔDBF,∴∠A=∠D,∠ECA=∠FBD.?
∴AE//DF,EC//BF.?
解题策略:证明两直线平行,常通过同位角相等、内错角相等、同旁内角互补或平行于同一线的两直线平行证得.具体采用哪种方法要根据已知条件进行灵活选取.
如图,点A,B,C在一条直线上,点E在BD上,且ΔABD≌ΔEBC.
(1)判断AC与BD的位置关系,并说明理由;
(2)判断直线AD与直线CE的位置关系,并说明理由.
解:(1)AC⊥BD.理由如下:
∵ΔABD≌ΔEBC,∵∠ABD=∠EBC.
∵点A,B,C在一条直线上,
∴∠ABD+∠EBC=180°(平角等于180°).
∴∠ABD=∠EBC=90°,∴AC⊥BD.
(2)直线AD⊥直线CE.理由如下:
如图,延长CE交AD于点F.
∵ΔABD≌ΔEBC,
∴∠D=∠C.
在RtΔABD中.∴∠A+∠D=90°,
∠A+∠C=90°∴∠DFC=∠A+∠C=90°,
直线AD⊥直线CE.
解题策略:证明两直线垂直可转化为证明它们的夹角为90°.当题目中没有给出任何角的度数时,常常借助两个等角的和是180°来证明.
变式练习:
如图,点A,B,C,D在一条直线上,点E,F是直线AD上方的点,连接AE,CE,BF,DF,若ΔACE≌ΔFDB,FD=3,AD=8.
(1)直线CE与DF是否平行?说明理由;
(2)求CD的长;
(3)若∠E=26°,∠F=53°,求∠ACE的度数.
解:(1)CE//DF.?
理由:∵ΔACE≌ΔFDB,
∴∠ACE=∠D,?
∴CE//DF.
(2)ΔACE≌ΔFDB,?
∴AC=FD=3.?
∵AD=8,∴CD=AD-AC=8-3=5.?
(3)∵ΔACE≌ΔFDB,∴∠A=∠F=53°.?
∴∠ACE=180°-∠A-∠E=180°-53°-?26°=101°.
2、如图,E为AB上一点,AC⊥AB于点A,DB⊥AB于点B,ΔACE≌ΔBED.
(1)试猜想线段CE与DE的位置关系,并证明你的结论;
(2)求证:AB=AC+BD.
(1)解:CE⊥DE.
证明如下:???????
∵AC⊥AB,?
∴∠A=90°.????????????
∴∠C+∠CEA=90°.?
∵ΔACE≌ΔBED,??
∴∠C=∠DEB.?
∴∠DEB+∠CEA=90°.?
∴∠CED=180°-∠DEB-∠CEA=180°-?90°=90°∴CE⊥DE.
(2)证明:∵ΔACE≌ΔBED,
∴AC=BE,AE=BD.
∴AB=BE+AE=AC+BD.
3、如图,已知AE⊥AB,ΔACE≌ΔAFB,CE分别与AB,BF交于点D,M.线段CE与FB有什么关系?请证明你的结论.
解:CE=FB,且?CE⊥FB.
证明如下:
AE⊥AB,
∵∠BAE=90°.
∴∠E+∠ADE=90°.
∵ΔACE≌ΔAFB,∴∠E=∠B,CE=FB.?
又∵∠ADE=∠BDM,
∴∠E+∠ADE=∠B+∠BDM=90°.
∴∠BMD=180°-∠B-∠BDM=90°.
∴CE⊥FB.?
基础练习:
如图,若ΔABC≌ΔADE,则下列结论中一定成立的是(?C)
AC=DE
B.AB=AE
C.∠BAD=∠CAE
D.∠ABC=∠AED
2、如图,已知ΔABC≌ΔDCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论错误的是(?C)
A.∠D=60°
B.∠DBC=40°
C.BE=10
D.AC=DB
1题
2题
3题
如图中的两个三角形全等,图中的字母a,b,c表示三角形的边长,则∠1的度数为??50°
4、如图,已知ΔACE≌ΔDBF,CE=BF,AD=9,BC=1.
(1)求证:CE//BF;
(2)求AC的长度.
解:(1)证明:∵ΔACE≌ΔDBF,∴∠ACE=∠DBF,∴CE//BF;
(2)∵ΔACE≌ΔDBF,∴AC=BD,AC-BC=BD-BC,?
∴AB=CD=(AD-BC)÷2=4,∴AC=AB+BC=4+1=5.?
5、如图,ΔABC≌ΔADE,分别延长BC,ED交于点F.
(1)求证:∠ACF+∠E=180°;
(2)若∠BAC=55°,∠CAD=60°,求∠F的度数.
解:(1)证明:∵ΔABC≌ΔADE,∴∠E=∠ACB.
∵∠ACF+∠ACB=180°,∴∠ACF+∠E=180°;?
(2)∵ΔABC≌ΔADE,∴∠EAD≌∠BAC=55°.∵∠CAD=60°,?
∴∠CAE=∠CAD+∠EAD=115°.?
∵∠ACF+∠E+∠CAE+∠F=360°,∠ACF+∠E=180°,?
∴180°+115°+∠F=360°∴∠F=65°.?
综合题探究
6、如图,在ΔABC中,∠C=90°,∠A≠∠B,AB=10,AC=8,BC=6,D是AB的中点,E是BC的中点,∠DEB=90°,DE=4.动点P以每秒2个单位长度的速度,从点A出发沿AC边向点C运动,同时动点Q以每秒a个单位长度的速度也从点B出发,沿BA边向点A运动,若ΔAPQ与ΔDEB全等,直接写出a的值.
解:a的值为2.4或2.5.设运动时间为ts,则AP=2t,BQ=at,AQ=10-at.
∵∠C=∠DEB=90°,∴AC//DE,
∴∠A=∠EDB≠∠B.
若ΔAPQ≌ΔDEB,
∴AP=DE=4,AQ=DB=5,
∴2t=4,10-at=5,∴t=2,a=2.5;
若ΔAQP≌ΔDEB.
∴AP=DB=5,AQ=DE=4,∴2t=5,10-at=4,∴t=2.5,a=2.4;
综上所述,a的值为2.4或2.5
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
