人教版八上高分笔记之导与练 12.2.1 用“SSS”判断三角形全等(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 12.2.1 用“SSS”判断三角形全等(原卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 19:37:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
12.2全等三角形的判定
用SSS判定三角形全等
知识要点:
三边?
?的两个三角形全等,简写成_SSS?
易错点睛:
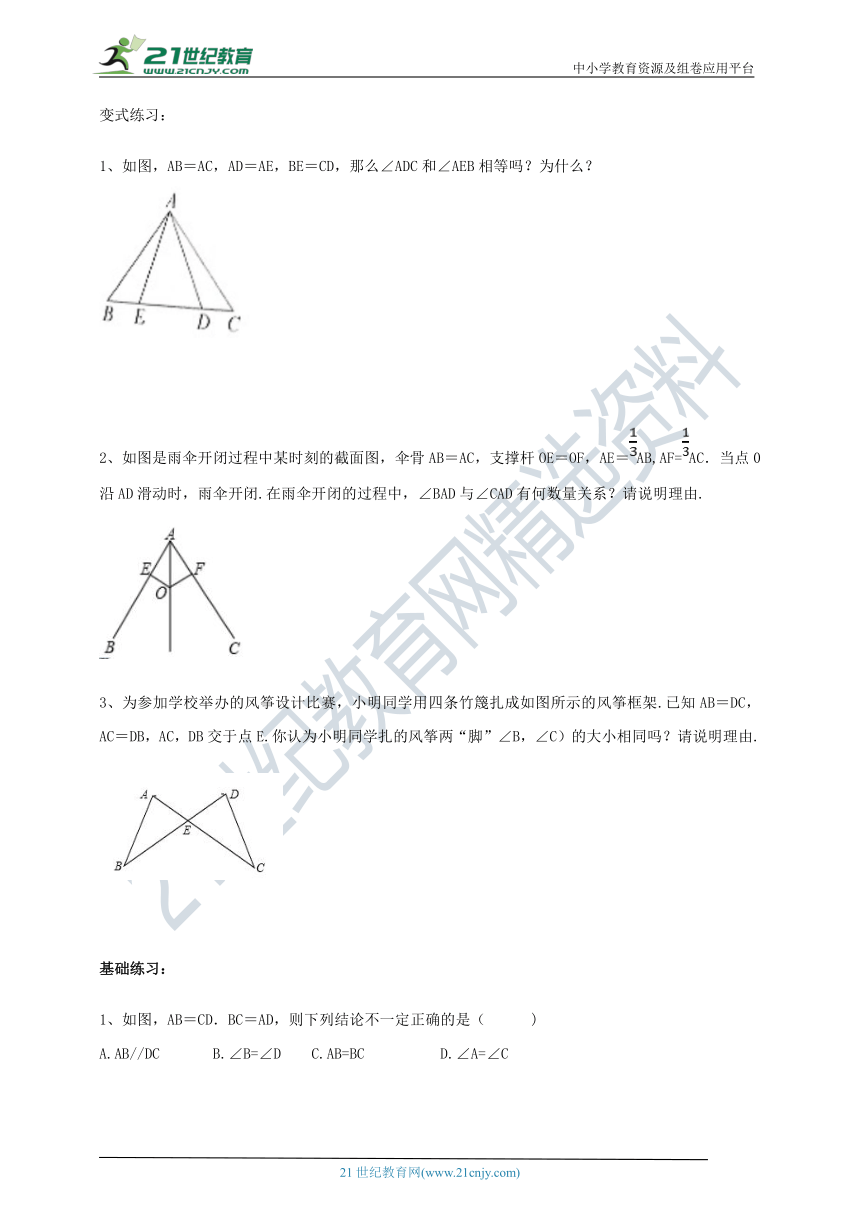
如图,点B.E.C.F在同一直线上,AB=DE,AC=DF,BE=CF.求证:ΔABC≌ΔDEF.
【点睛】?易把部分(BE=CF)当作对应边而出错。
典型例题:
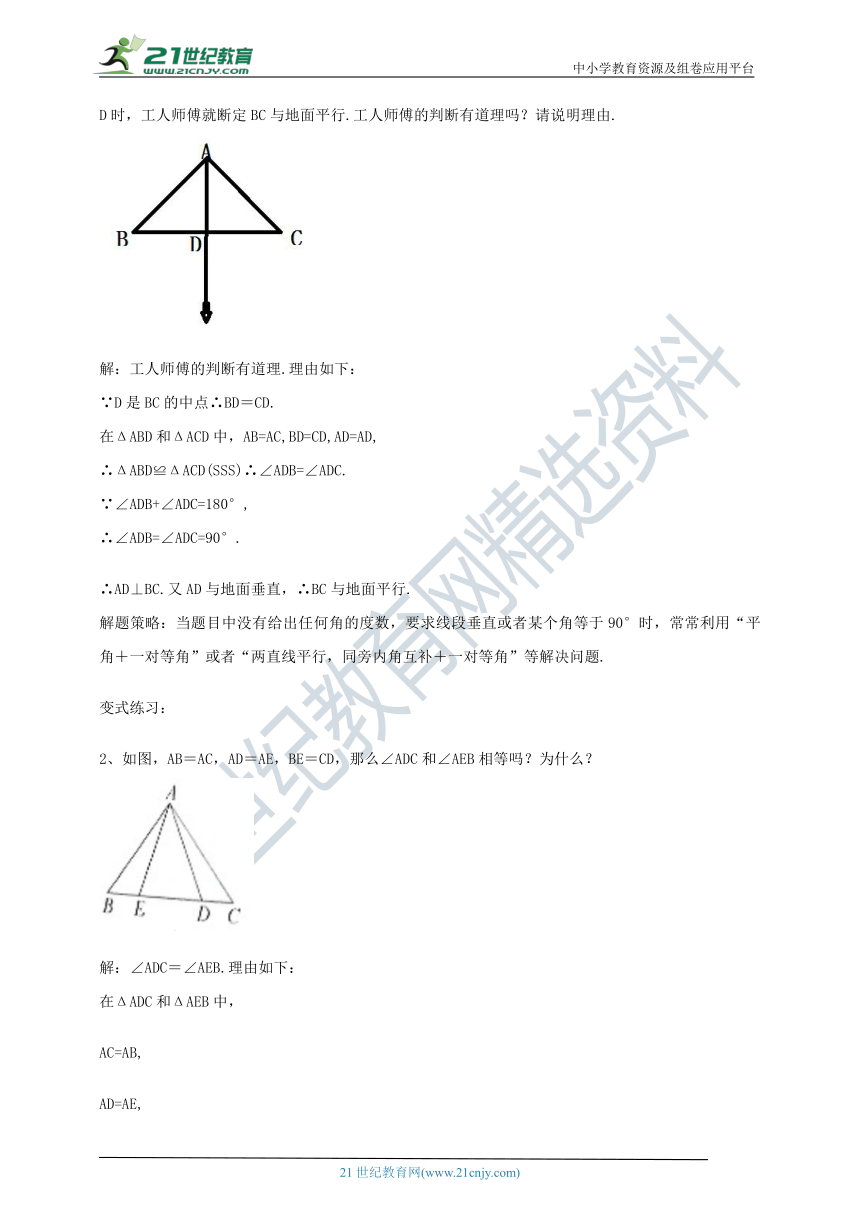
例、如图是工人师傅自已设计的测量水平的仪器.仪器中的AB=AC,D是BC的中点,当铅垂线经过点D时,工人师傅就断定BC与地面平行.工人师傅的判断有道理吗?请说明理由.
解题策略:当题目中没有给出任何角的度数,要求线段垂直或者某个角等于90°时,常常利用“平角+一对等角”或者“两直线平行,同旁内角互补+一对等角”等解决问题.
变式练习:
如图,AB=AC,AD=AE,BE=CD,那么∠ADC和∠AEB相等吗?为什么?
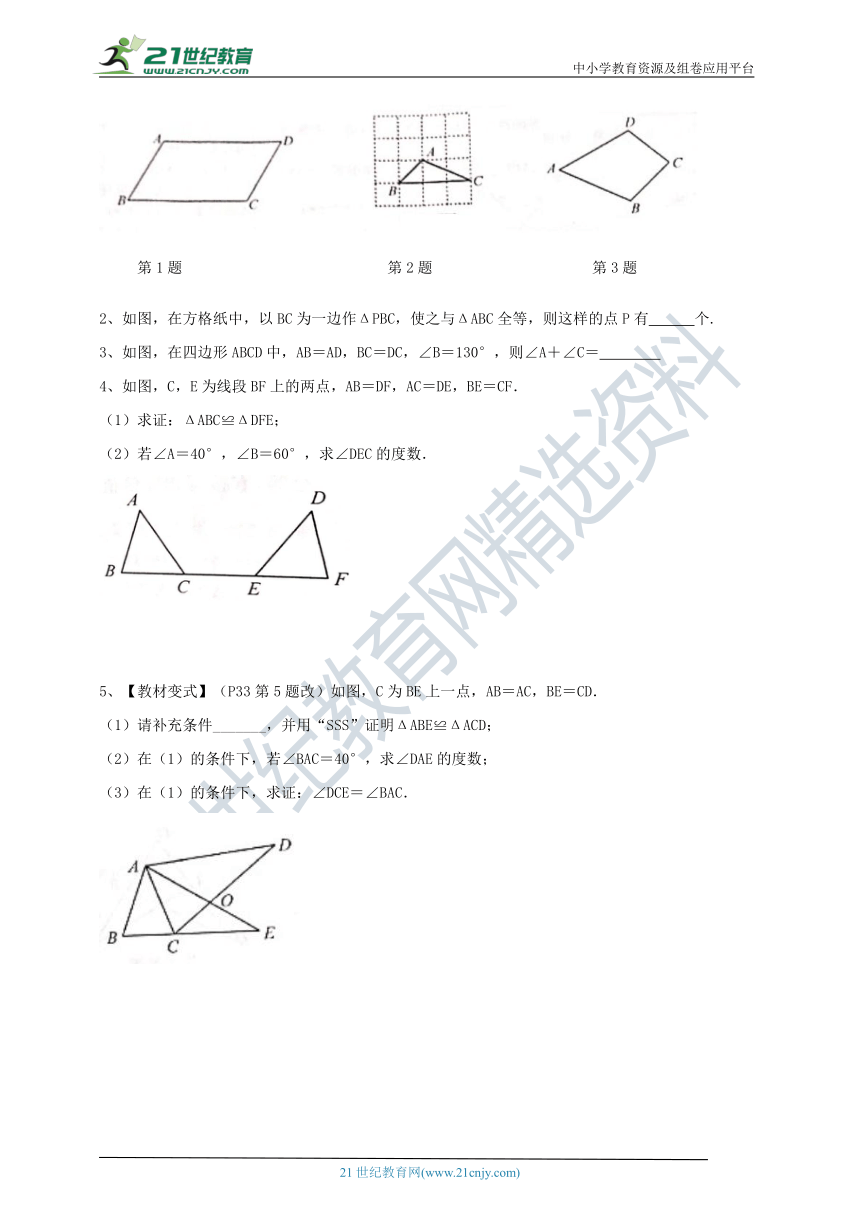
2、如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC.当点0沿AD滑动时,雨伞开闭.在雨伞开闭的过程中,∠BAD与∠CAD有何数量关系?请说明理由.
3、为参加学校举办的风筝设计比赛,小明同学用四条竹篾扎成如图所示的风筝框架.已知AB=DC,AC=DB,AC,DB交于点E.你认为小明同学扎的风筝两“脚”∠B,∠C)的大小相同吗?请说明理由.
基础练习:
如图,AB=CD.BC=AD,则下列结论不一定正确的是(??
)
A.AB//DC
B.∠B=∠D
C.AB=BC?
D.∠A=∠C
第1题
第2题
第3题
如图,在方格纸中,以BC为一边作ΔPBC,使之与ΔABC全等,则这样的点P有?
?个.
3、如图,在四边形ABCD中,AB=AD,BC=DC,∠B=130°,则∠A+∠C=
4、如图,C,E为线段BF上的两点,AB=DF,AC=DE,BE=CF.
(1)求证:ΔABC≌ΔDFE;
(2)若∠A=40°,∠B=60°,求∠DEC的度数.
【教材变式】(P33第5题改)如图,C为BE上一点,AB=AC,BE=CD.
(1)请补充条件_______,并用“SSS”证明ΔABE≌ΔACD;
(2)在(1)的条件下,若∠BAC=40°,求∠DAE的度数;
(3)在(1)的条件下,求证:∠DCE=∠BAC.
6、如图,A为BE上一点,D为AF上一点,AB=AD,AE=AF,BF=DE.
(1)求证:∠E=∠F;
(2)求证:BF⊥CE;
(3)延长ED至点C,使CD=CB,若∠E=20°,求∠BCE的度数.
答案:
知识要点:
三边?对应相等?的两个三角形全等,简写成_SSS?
易错点睛:
如图,点B.E.C.F在同一直线上,AB=DE,AC=DF,BE=CF.求证:ΔABC≌ΔDEF.
证明:∵BE=CF∴BC=EF
在△ABC和△DEF中AB=DE,AC=DF,BC=EF
∴△ABC≌△DEF(SSS)
【点睛】?易把部分(BE=CF)当作对应边而出错。
典型例题:
例、如图是工人师傅自已设计的测量水平的仪器.仪器中的AB=AC,D是BC的中点,当铅垂线经过点D时,工人师傅就断定BC与地面平行.工人师傅的判断有道理吗?请说明理由.
解:工人师傅的判断有道理.理由如下:
∵D是BC的中点∴BD=CD.
在ΔABD和ΔACD中,AB=AC,BD=CD,AD=AD,?
∴ΔABD≌ΔACD(SSS)∴∠ADB=∠ADC.
∵∠ADB+∠ADC=180°,?
∴∠ADB=∠ADC=90°.
∴AD⊥BC.又AD与地面垂直,∴BC与地面平行.
解题策略:当题目中没有给出任何角的度数,要求线段垂直或者某个角等于90°时,常常利用“平角+一对等角”或者“两直线平行,同旁内角互补+一对等角”等解决问题.
变式练习:
如图,AB=AC,AD=AE,BE=CD,那么∠ADC和∠AEB相等吗?为什么?
解:∠ADC=∠AEB.理由如下:
在ΔADC和ΔAEB中,
AC=AB,?
AD=AE,
CD=BE,?
∴ΔADC≌ΔAEB(SSS).∴∠ADC=∠AEB.?
2、如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=B,AF=AC.当点0沿AD滑动时,雨伞开闭.在雨伞开闭的过程中,∠BAD与∠CAD有何数量关系?请说明理由.
解:∠BAD=∠CAD.
理由如下:
∵AB=AC,AE=AB,AF=AC,∴AE=AF.?
在ΔAEO和ΔAFO中,
OE=0F,?
AE=AF,?
AO=A0,?
∴ΔAEO≌ΔAFO(SSS).?
∴∠EAO=∠FAO,即∠BAD=∠CAD.-
3、为参加学校举办的风筝设计比赛,小明同学用四条竹篾扎成如图所示的风筝框架.已知AB=DC,AC=DB,AC,DB交于点E.你认为小明同学扎的风筝两“脚”∠B,∠C)的大小相同吗?请说明理由.
连接AD,
∵在△ADB和△DAC中
∴△ADB≌△DAC(SSS),
∴∠B=∠C.
基础练习:
如图,AB=CD.BC=AD,则下列结论不一定正确的是(??C
)
A.AB//DC
B.∠B=∠D
C.AB=BC?
D.∠A=∠C
第1题
第2题
第3题
如图,在方格纸中,以BC为一边作ΔPBC,使之与ΔABC全等,则这样的点P有?3?个.
3、如图,在四边形ABCD中,AB=AD,BC=DC,∠B=130°,则∠A+∠C=100°
4、如图,C,E为线段BF上的两点,AB=DF,AC=DE,BE=CF.
(1)求证:ΔABC≌ΔDFE;
(2)若∠A=40°,∠B=60°,求∠DEC的度数.
解:(1)证明:“BE=CF,··BE-CE=CF-CE,即BC=EF.
在ΔABC与ΔDFE中,AB=DF,?AC=DE,BC=EF,∴ΔABC≌ΔDFE(SSS);?
(2)∵ΔABC≌ΔDFE,∴∠D=∠A=40°,∠F=∠B=60°,∠DEC=∠D+∠F=100°.
【教材变式】(P33第5题改)如图,C为BE上一点,AB=AC,BE=CD.
(1)请补充条件_______,并用“SSS”证明ΔABE≌ΔACD;
(2)在(1)的条件下,若∠BAC=40°,求∠DAE的度数;
(3)在(1)的条件下,求证:∠DCE=∠BAC.
解:(1)AE=AD.证明略;
(2)∠DAE=∠BAC=40°;
(3)证明:∵ΔABE≌ΔACD·∴∠D=∠E,
又∵∠AOD=∠COE,∴∠DCE=∠DAE=∠BAC.
6、如图,A为BE上一点,D为AF上一点,AB=AD,AE=AF,BF=DE.
(1)求证:∠E=∠F;
(2)求证:BF⊥CE;
(3)延长ED至点C,使CD=CB,若∠E=20°,求∠BCE的度数.
(1)在ΔABF与ΔADE中,AB=AD,AF=AE,BF=DE,∴ΔABF≌ΔADE(SSS)
∴∠E=∠F
证明:∵ΔABF≌ΔADE.∴∠BAF=∠EAD.:∠BAF+∠EAD=180°,
∴∠BAF=∠EAD=90°,∴∠F+∠ABF=90°.?
∵∠E=∠F.∴∠E+∠ABF=90°,∴CE⊥BF;?
(3)连接AC.∵∠E=20°,∠EAD=90°,∴∠ADE=70°,∴∠ADC=110°.
在ΔABC与ΔADC中,AB=AD,AC=AC,BC=DC,∴ΔABC≌ΔADC(SSS).∴∠ABC=∠ADC=110°.
∵ABC+∠BCE+∠E=180°,即110°+20°+∠BCE=180°.∴∠BCE=50°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2全等三角形的判定
用SSS判定三角形全等
知识要点:
三边?
?的两个三角形全等,简写成_SSS?
易错点睛:
如图,点B.E.C.F在同一直线上,AB=DE,AC=DF,BE=CF.求证:ΔABC≌ΔDEF.
【点睛】?易把部分(BE=CF)当作对应边而出错。
典型例题:
例、如图是工人师傅自已设计的测量水平的仪器.仪器中的AB=AC,D是BC的中点,当铅垂线经过点D时,工人师傅就断定BC与地面平行.工人师傅的判断有道理吗?请说明理由.
解题策略:当题目中没有给出任何角的度数,要求线段垂直或者某个角等于90°时,常常利用“平角+一对等角”或者“两直线平行,同旁内角互补+一对等角”等解决问题.
变式练习:
如图,AB=AC,AD=AE,BE=CD,那么∠ADC和∠AEB相等吗?为什么?
2、如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC.当点0沿AD滑动时,雨伞开闭.在雨伞开闭的过程中,∠BAD与∠CAD有何数量关系?请说明理由.
3、为参加学校举办的风筝设计比赛,小明同学用四条竹篾扎成如图所示的风筝框架.已知AB=DC,AC=DB,AC,DB交于点E.你认为小明同学扎的风筝两“脚”∠B,∠C)的大小相同吗?请说明理由.
基础练习:
如图,AB=CD.BC=AD,则下列结论不一定正确的是(??
)
A.AB//DC
B.∠B=∠D
C.AB=BC?
D.∠A=∠C
第1题
第2题
第3题
如图,在方格纸中,以BC为一边作ΔPBC,使之与ΔABC全等,则这样的点P有?
?个.
3、如图,在四边形ABCD中,AB=AD,BC=DC,∠B=130°,则∠A+∠C=
4、如图,C,E为线段BF上的两点,AB=DF,AC=DE,BE=CF.
(1)求证:ΔABC≌ΔDFE;
(2)若∠A=40°,∠B=60°,求∠DEC的度数.
【教材变式】(P33第5题改)如图,C为BE上一点,AB=AC,BE=CD.
(1)请补充条件_______,并用“SSS”证明ΔABE≌ΔACD;
(2)在(1)的条件下,若∠BAC=40°,求∠DAE的度数;
(3)在(1)的条件下,求证:∠DCE=∠BAC.
6、如图,A为BE上一点,D为AF上一点,AB=AD,AE=AF,BF=DE.
(1)求证:∠E=∠F;
(2)求证:BF⊥CE;
(3)延长ED至点C,使CD=CB,若∠E=20°,求∠BCE的度数.
答案:
知识要点:
三边?对应相等?的两个三角形全等,简写成_SSS?
易错点睛:
如图,点B.E.C.F在同一直线上,AB=DE,AC=DF,BE=CF.求证:ΔABC≌ΔDEF.
证明:∵BE=CF∴BC=EF
在△ABC和△DEF中AB=DE,AC=DF,BC=EF
∴△ABC≌△DEF(SSS)
【点睛】?易把部分(BE=CF)当作对应边而出错。
典型例题:
例、如图是工人师傅自已设计的测量水平的仪器.仪器中的AB=AC,D是BC的中点,当铅垂线经过点D时,工人师傅就断定BC与地面平行.工人师傅的判断有道理吗?请说明理由.
解:工人师傅的判断有道理.理由如下:
∵D是BC的中点∴BD=CD.
在ΔABD和ΔACD中,AB=AC,BD=CD,AD=AD,?
∴ΔABD≌ΔACD(SSS)∴∠ADB=∠ADC.
∵∠ADB+∠ADC=180°,?
∴∠ADB=∠ADC=90°.
∴AD⊥BC.又AD与地面垂直,∴BC与地面平行.
解题策略:当题目中没有给出任何角的度数,要求线段垂直或者某个角等于90°时,常常利用“平角+一对等角”或者“两直线平行,同旁内角互补+一对等角”等解决问题.
变式练习:
如图,AB=AC,AD=AE,BE=CD,那么∠ADC和∠AEB相等吗?为什么?
解:∠ADC=∠AEB.理由如下:
在ΔADC和ΔAEB中,
AC=AB,?
AD=AE,
CD=BE,?
∴ΔADC≌ΔAEB(SSS).∴∠ADC=∠AEB.?
2、如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=B,AF=AC.当点0沿AD滑动时,雨伞开闭.在雨伞开闭的过程中,∠BAD与∠CAD有何数量关系?请说明理由.
解:∠BAD=∠CAD.
理由如下:
∵AB=AC,AE=AB,AF=AC,∴AE=AF.?
在ΔAEO和ΔAFO中,
OE=0F,?
AE=AF,?
AO=A0,?
∴ΔAEO≌ΔAFO(SSS).?
∴∠EAO=∠FAO,即∠BAD=∠CAD.-
3、为参加学校举办的风筝设计比赛,小明同学用四条竹篾扎成如图所示的风筝框架.已知AB=DC,AC=DB,AC,DB交于点E.你认为小明同学扎的风筝两“脚”∠B,∠C)的大小相同吗?请说明理由.
连接AD,
∵在△ADB和△DAC中
∴△ADB≌△DAC(SSS),
∴∠B=∠C.
基础练习:
如图,AB=CD.BC=AD,则下列结论不一定正确的是(??C
)
A.AB//DC
B.∠B=∠D
C.AB=BC?
D.∠A=∠C
第1题
第2题
第3题
如图,在方格纸中,以BC为一边作ΔPBC,使之与ΔABC全等,则这样的点P有?3?个.
3、如图,在四边形ABCD中,AB=AD,BC=DC,∠B=130°,则∠A+∠C=100°
4、如图,C,E为线段BF上的两点,AB=DF,AC=DE,BE=CF.
(1)求证:ΔABC≌ΔDFE;
(2)若∠A=40°,∠B=60°,求∠DEC的度数.
解:(1)证明:“BE=CF,··BE-CE=CF-CE,即BC=EF.
在ΔABC与ΔDFE中,AB=DF,?AC=DE,BC=EF,∴ΔABC≌ΔDFE(SSS);?
(2)∵ΔABC≌ΔDFE,∴∠D=∠A=40°,∠F=∠B=60°,∠DEC=∠D+∠F=100°.
【教材变式】(P33第5题改)如图,C为BE上一点,AB=AC,BE=CD.
(1)请补充条件_______,并用“SSS”证明ΔABE≌ΔACD;
(2)在(1)的条件下,若∠BAC=40°,求∠DAE的度数;
(3)在(1)的条件下,求证:∠DCE=∠BAC.
解:(1)AE=AD.证明略;
(2)∠DAE=∠BAC=40°;
(3)证明:∵ΔABE≌ΔACD·∴∠D=∠E,
又∵∠AOD=∠COE,∴∠DCE=∠DAE=∠BAC.
6、如图,A为BE上一点,D为AF上一点,AB=AD,AE=AF,BF=DE.
(1)求证:∠E=∠F;
(2)求证:BF⊥CE;
(3)延长ED至点C,使CD=CB,若∠E=20°,求∠BCE的度数.
(1)在ΔABF与ΔADE中,AB=AD,AF=AE,BF=DE,∴ΔABF≌ΔADE(SSS)
∴∠E=∠F
证明:∵ΔABF≌ΔADE.∴∠BAF=∠EAD.:∠BAF+∠EAD=180°,
∴∠BAF=∠EAD=90°,∴∠F+∠ABF=90°.?
∵∠E=∠F.∴∠E+∠ABF=90°,∴CE⊥BF;?
(3)连接AC.∵∠E=20°,∠EAD=90°,∴∠ADE=70°,∴∠ADC=110°.
在ΔABC与ΔADC中,AB=AD,AC=AC,BC=DC,∴ΔABC≌ΔADC(SSS).∴∠ABC=∠ADC=110°.
∵ABC+∠BCE+∠E=180°,即110°+20°+∠BCE=180°.∴∠BCE=50°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
