人教版八上高分笔记之导与练 12.2.2 用“SAS”判断三角形全等(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 12.2.2 用“SAS”判断三角形全等(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
12.2全等三角形的判定
用SAS判定三角形全等
知识要点:
有两边和它们的?
??分别相等的两个三角形全等,简写成??
或?
?
尝试应用:
1.如图,AB=AD.∠1=∠2,则ΔABC≌ΔADC,理由是
1题
2题
3题
如图,AB=AC,AD=AE,则?ΔABD≌AACE,理由是
?
如图,AC,BD交于点E,AE=CE,根据SAS得到ΔABE≌ΔCDE,只需补充条件:
_-_____
易错点睛:
已知ΔABC?和ΔDEF中,AB=DE,AC=DF,∠C=∠F,则ΔABC与ΔDEF是否一定全等?试说明理由。
典型例题:
类型一
利用全等进行有关的计算或证明
如图,点A,B,C,D在一条直线上,EA//FB,EA=FB,AB=CD.
求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
解题策略:在证明两个三角形全等时,如果已知两组对应边分别相等,一般要去寻找第三条边对应相等或两组对应边的夹角相等,利用“SSS”或“SAS”证明两个三角形全等.
变式练习:
1、如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
求证:∠D=∠2;
若EF//AC,∠D=78°,求∠BAC的度数.
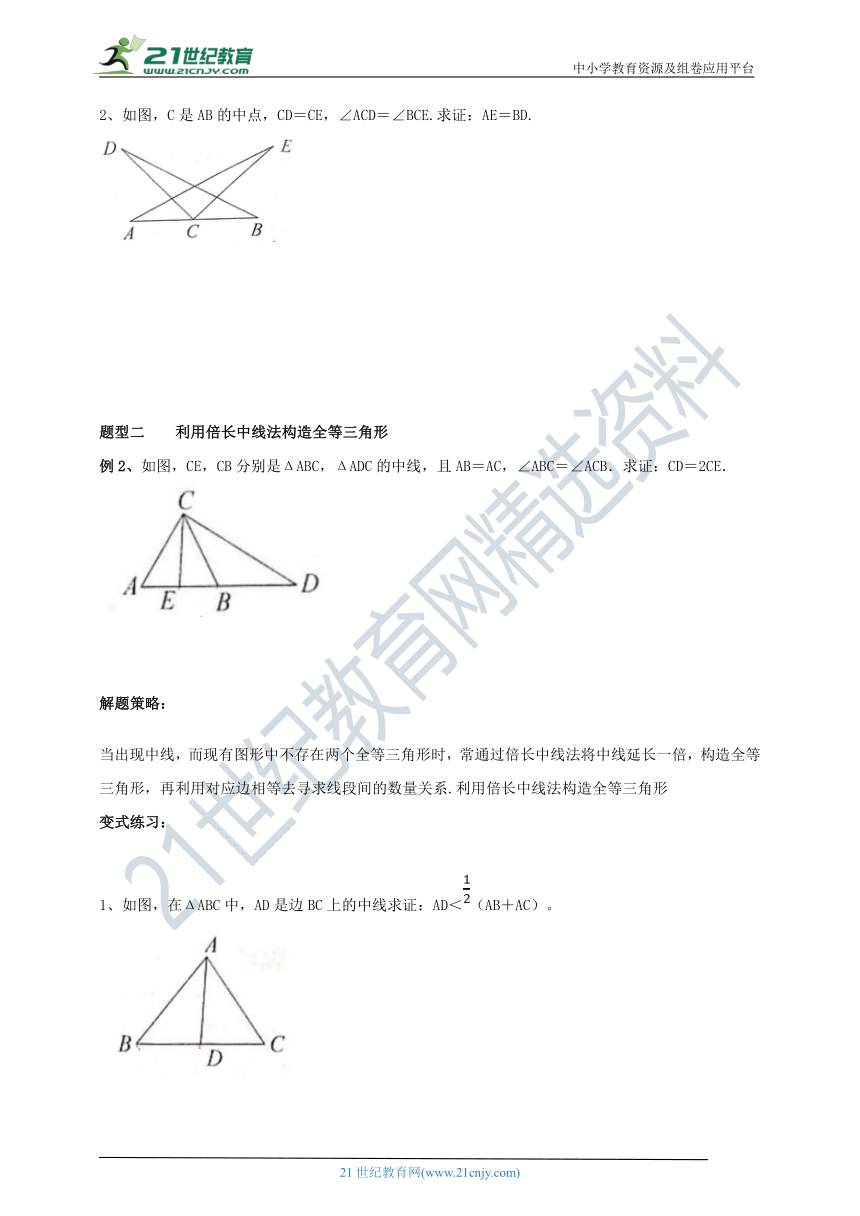
2、如图,C是AB的中点,CD=CE,∠ACD=∠BCE.求证:AE=BD.
题型二
利用倍长中线法构造全等三角形
例2、如图,CE,CB分别是ΔABC,ΔADC的中线,且AB=AC,∠ABC=∠ACB.求证:CD=2CE.
解题策略:
当出现中线,而现有图形中不存在两个全等三角形时,常通过倍长中线法将中线延长一倍,构造全等三角形,再利用对应边相等去寻求线段间的数量关系.利用倍长中线法构造全等三角形
变式练习:
如图,在ΔABC中,AD是边BC上的中线求证:AD<(AB+AC)。
2、如图,AB=AE,ABLAE,AD=AC,AD⊥AC,M为BC的中点.求证:DE=2AM.
基础练习:
如图,AB=AD,AC=AE,添加下列条件,不一定能得到ΔABC≌ΔADE的是(?
)
A.BC=DE
B.∠BAC=∠DAE
C.∠C=∠E
D.∠BAD=∠CAE
第1题
第2题
第3题
如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为?
3、如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为??
?
4、如图,线段AD,CE相交于点B,BC=BD,AB=EB.求证:ΔACD≌ΔEDC.
5、如图,在ΔABC中,点D,E,F分别在边BC,AB,AC上,DE=DF,∠EDF=∠B,BE=DC.
(1)求证:BC=FC+BE;
(2)若∠A=100°,求∠EDF的度数.
综合探究:
6、在ΔABC和ΔCDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.
(1)如图1,当α=90°时,求证:①ΔACE≌ΔBCD,②AE⊥BD;
(2)如图2,当α=60°时,求∠AFB的度数;
(3)如图3,直接写出∠AFD的度数为______(用含α的式子表示).
答案:
知识要点:
有两边和它们的?夹角??分别相等的两个三角形全等,简写成??边角边
或?SAS?
尝试应用:
1.如图,AB=AD.∠1=∠2,则ΔABC≌ΔADC,理由是SAS
1题
2题
3题
如图,AB=AC,AD=AE,则?ΔABD≌AACE,理由是SAS?
如图,AC,BD交于点E,AE=CE,根据SAS得到ΔABE≌ΔCDE,只需补充条件:BE=DE
易错点睛:
已知ΔABC?和ΔDEF中,AB=DE,AC=DF,∠C=∠F,则ΔABC与ΔDEF是否
一定全等?试说明理由。
【点睛】SAS中的A应是S与S的夹角.不一定全等,反例如下:
【解】
典型例题:
类型一
利用全等进行有关的计算或证明
如图,点A,B,C,D在一条直线上,EA//FB,EA=FB,AB=CD.
求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
证明:∵EA//FB,∠A=∠FBD.∴AB=CD,∴AB+BC=CD+BC,即AC=BD.?
在ΔEAC和ΔFBD中,EA=FB,?∠A=∠FBD,?AC=BD,?
∴ΔEAC≌ΔFBD(SAS)∴∠E=∠F.
(2)解:由(1)知ΔEAC≌ΔFBD,∴∠ECA=∠D=80°.
∠A=40°,∴∠E=180°-∠A-∠ECA=180°-40?-80?=60?
解题策略:在证明两个三角形全等时,如果已知两组对应边分别相等,一般要去寻找第三条边对应相等或两组对应边的夹角相等,利用“SSS”或“SAS”证明两个三角形全等.
变式练习:
如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
求证:∠D=∠2;
若EF//AC,∠D=78°,求∠BAC的度数.
证明:在ΔCDA和ΔBEF中,
CD=BE,?
∠1=∠B,?
CA=BF.?
∴ΔCDA≌ΔBEF(SAS),∴∠D=∠2.
(2)解:∵∠D=∠2,∠D=78°,∴∠2=78°.
∵EF//AC,∴∠BAC=∠2=78°.
如图,C是AB的中点,CD=CE,∠ACD=∠BCE.求证:AE=BD.
证明:C是AB的中点,∴AC=BC.
∠ACD=∠BCE,
∠ACD+∠DCE=∠BCE+∠DCE,即?
∠ACE=∠BCD.?
在ΔACE和ΔBCD中,AC=BC,?∠ACE=∠BCD,CE=CD,
ΔACE≌ΔBCD(SAS)∴AE=BD.
题型二
利用倍长中线法构造全等三角形
例2、如图,CE,CB分别是ΔABC,ΔADC的中线,且AB=AC,∠ABC=∠ACB.求证:CD=2CE.
证明:如图,延长CE至点F,使EF=CE,则CF=2CE,
连接FB.∵CE是ΔABC的中线,∴AE=BE.
在ΔBEF和ΔAEC中,BE=AE,∠BEF=∠AEC,EF=EC,∴ΔBEF≌ΔAEC(SAS).
∴∠EBF=∠A,BF=AC.又∠ABC=∠ACB,
∴∠CBD=∠A+∠ACB=∠EBF+∠ABC=∠CBF.∵CB是ΔADC的中线,∴AB=BD.
又AB=AC,AC=BF,∴BF=BD.
在ΔCBF和ΔCBD中,CB=CB,?∠CBF=∠CBD,BF=BD,
∴ΔCBF≌ΔCBD(SAS)·∴CF=CD·∴CD=2CE.
解题策略:
当出现中线,而现有图形中不存在两个全等三角形时,常通过倍长中线法将中线延长一倍,构造全等三角形,再利用对应边相等去寻求线段间的数量关系.利用倍长中线法构造全等三角形
变式练习:
如图,在ΔABC中,AD是边BC上的中线求证:AD<(AB+AC)。
证明:如图,延长AD至点E,使DE=AD,则AE=2AD,连接BE.
∵AD是边BC上的中线,
∴DC=DB.
在ΔACD和ΔEBD中,DC=DB,?∠ADC=∠EDB,AD=ED,?
∴ΔACD≌ΔEBD(SAS).?
∴AC=EB.?
在ΔABE中,AE<AB+EB,
∴2AD2、如图,AB=AE,ABLAE,AD=AC,AD⊥AC,M为BC的中点.求证:DE=2AM.
证明:如图,延长AM?至点N,使MN=AM,则NA=2AM,连接BN.
∵M为BC的中点,∴CM=BM.
在ΔAMC和ΔNMB中,AM=NM,?∠AMC=∠NMB,?CM=BM,?
∴ΔAMC≌ΔNMB(SAS),
∴AC=NB,∠C=∠NBM.∴AD=AC,∴AD=BN.
∵AB⊥AE,AD⊥AC,∴∠EAB=∠DAC=90°,
∴∠EAD+∠BAC=360°-∠EAB-∠DAC=180°,
∴∠ABN=∠ABC+∠NBM=∠ABC+∠C=180°-?∠BAC=∠EAD.?
在ΔEAD和ΔABN中,AE=BA,∠EAD=∠ABN,AD=BN,?
.ΔEAD≌ΔABN(SAS),∴DE=NA=2AM.?
基础练习:
如图,AB=AD,AC=AE,添加下列条件,不一定能得到ΔABC≌ΔADE的是(?C
)
A.BC=DE
B.∠BAC=∠DAE
C.∠C=∠E
D.∠BAD=∠CAE
第1题
第2题
第3题
2、如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为?30°
3、如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为??82°?
4、如图,线段AD,CE相交于点B,BC=BD,AB=EB.求证:ΔACD≌ΔEDC.
证明:在ΔABC与ΔEBD中,
AB=BE,∠ABC=∠EBD,BC=BD,
∴ΔABC≌ΔEBD(SAS),?
∴AC=ED,∠A=∠E.AB=EB,BC=BD,
∴.AB+BD=EB+BC,?
即AD=EC.
在ΔACD与ΔEDC中,AC=ED,∠A=∠E,AD=EC,
∴.ΔACD≌ΔEDC(SAS).?
5、如图,在ΔABC中,点D,E,F分别在边BC,AB,AC上,DE=DF,∠EDF=∠B,BE=DC.
(1)求证:BC=FC+BE;
(2)若∠A=100°,求∠EDF的度数.
(1)思路:证ΔBDE≌ΔCFD得到FC=BD∵BE=DC,∴BC=BD+DC=FC+BE
(2)∵ΔBDE≌ΔCFD,∴∠B=∠C.
∵∠A=100°,∴∠B=40°.∴∠EDF=∠B,∴∠EDF=40°.
6、在ΔABC和ΔCDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.
(1)如图1,当α=90°时,求证:①ΔACE≌ΔBCD,②AE⊥BD;
(2)如图2,当α=60°时,求∠AFB的度数;
(3)如图3,直接写出∠AFD的度数为______(用含α的式子表示).
解:思路:(1)证明:证ΔACE≌ΔBCD,∴∠CAE=∠CBD,:∠AFB=∠ACB=90°,∴AE⊥BD;
(2)同(1)可得∠AFB=∠ACB=60°;
(3)同(1)可得∠AFB=∠ACB=α,故∠AFD=180°-α.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2全等三角形的判定
用SAS判定三角形全等
知识要点:
有两边和它们的?
??分别相等的两个三角形全等,简写成??
或?
?
尝试应用:
1.如图,AB=AD.∠1=∠2,则ΔABC≌ΔADC,理由是
1题
2题
3题
如图,AB=AC,AD=AE,则?ΔABD≌AACE,理由是
?
如图,AC,BD交于点E,AE=CE,根据SAS得到ΔABE≌ΔCDE,只需补充条件:
_-_____
易错点睛:
已知ΔABC?和ΔDEF中,AB=DE,AC=DF,∠C=∠F,则ΔABC与ΔDEF是否一定全等?试说明理由。
典型例题:
类型一
利用全等进行有关的计算或证明
如图,点A,B,C,D在一条直线上,EA//FB,EA=FB,AB=CD.
求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
解题策略:在证明两个三角形全等时,如果已知两组对应边分别相等,一般要去寻找第三条边对应相等或两组对应边的夹角相等,利用“SSS”或“SAS”证明两个三角形全等.
变式练习:
1、如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
求证:∠D=∠2;
若EF//AC,∠D=78°,求∠BAC的度数.
2、如图,C是AB的中点,CD=CE,∠ACD=∠BCE.求证:AE=BD.
题型二
利用倍长中线法构造全等三角形
例2、如图,CE,CB分别是ΔABC,ΔADC的中线,且AB=AC,∠ABC=∠ACB.求证:CD=2CE.
解题策略:
当出现中线,而现有图形中不存在两个全等三角形时,常通过倍长中线法将中线延长一倍,构造全等三角形,再利用对应边相等去寻求线段间的数量关系.利用倍长中线法构造全等三角形
变式练习:
如图,在ΔABC中,AD是边BC上的中线求证:AD<(AB+AC)。
2、如图,AB=AE,ABLAE,AD=AC,AD⊥AC,M为BC的中点.求证:DE=2AM.
基础练习:
如图,AB=AD,AC=AE,添加下列条件,不一定能得到ΔABC≌ΔADE的是(?
)
A.BC=DE
B.∠BAC=∠DAE
C.∠C=∠E
D.∠BAD=∠CAE
第1题
第2题
第3题
如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为?
3、如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为??
?
4、如图,线段AD,CE相交于点B,BC=BD,AB=EB.求证:ΔACD≌ΔEDC.
5、如图,在ΔABC中,点D,E,F分别在边BC,AB,AC上,DE=DF,∠EDF=∠B,BE=DC.
(1)求证:BC=FC+BE;
(2)若∠A=100°,求∠EDF的度数.
综合探究:
6、在ΔABC和ΔCDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.
(1)如图1,当α=90°时,求证:①ΔACE≌ΔBCD,②AE⊥BD;
(2)如图2,当α=60°时,求∠AFB的度数;
(3)如图3,直接写出∠AFD的度数为______(用含α的式子表示).
答案:
知识要点:
有两边和它们的?夹角??分别相等的两个三角形全等,简写成??边角边
或?SAS?
尝试应用:
1.如图,AB=AD.∠1=∠2,则ΔABC≌ΔADC,理由是SAS
1题
2题
3题
如图,AB=AC,AD=AE,则?ΔABD≌AACE,理由是SAS?
如图,AC,BD交于点E,AE=CE,根据SAS得到ΔABE≌ΔCDE,只需补充条件:BE=DE
易错点睛:
已知ΔABC?和ΔDEF中,AB=DE,AC=DF,∠C=∠F,则ΔABC与ΔDEF是否
一定全等?试说明理由。
【点睛】SAS中的A应是S与S的夹角.不一定全等,反例如下:
【解】
典型例题:
类型一
利用全等进行有关的计算或证明
如图,点A,B,C,D在一条直线上,EA//FB,EA=FB,AB=CD.
求证:∠E=∠F;
(2)若∠A=40°,∠D=80°,求∠E的度数.
证明:∵EA//FB,∠A=∠FBD.∴AB=CD,∴AB+BC=CD+BC,即AC=BD.?
在ΔEAC和ΔFBD中,EA=FB,?∠A=∠FBD,?AC=BD,?
∴ΔEAC≌ΔFBD(SAS)∴∠E=∠F.
(2)解:由(1)知ΔEAC≌ΔFBD,∴∠ECA=∠D=80°.
∠A=40°,∴∠E=180°-∠A-∠ECA=180°-40?-80?=60?
解题策略:在证明两个三角形全等时,如果已知两组对应边分别相等,一般要去寻找第三条边对应相等或两组对应边的夹角相等,利用“SSS”或“SAS”证明两个三角形全等.
变式练习:
如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
求证:∠D=∠2;
若EF//AC,∠D=78°,求∠BAC的度数.
证明:在ΔCDA和ΔBEF中,
CD=BE,?
∠1=∠B,?
CA=BF.?
∴ΔCDA≌ΔBEF(SAS),∴∠D=∠2.
(2)解:∵∠D=∠2,∠D=78°,∴∠2=78°.
∵EF//AC,∴∠BAC=∠2=78°.
如图,C是AB的中点,CD=CE,∠ACD=∠BCE.求证:AE=BD.
证明:C是AB的中点,∴AC=BC.
∠ACD=∠BCE,
∠ACD+∠DCE=∠BCE+∠DCE,即?
∠ACE=∠BCD.?
在ΔACE和ΔBCD中,AC=BC,?∠ACE=∠BCD,CE=CD,
ΔACE≌ΔBCD(SAS)∴AE=BD.
题型二
利用倍长中线法构造全等三角形
例2、如图,CE,CB分别是ΔABC,ΔADC的中线,且AB=AC,∠ABC=∠ACB.求证:CD=2CE.
证明:如图,延长CE至点F,使EF=CE,则CF=2CE,
连接FB.∵CE是ΔABC的中线,∴AE=BE.
在ΔBEF和ΔAEC中,BE=AE,∠BEF=∠AEC,EF=EC,∴ΔBEF≌ΔAEC(SAS).
∴∠EBF=∠A,BF=AC.又∠ABC=∠ACB,
∴∠CBD=∠A+∠ACB=∠EBF+∠ABC=∠CBF.∵CB是ΔADC的中线,∴AB=BD.
又AB=AC,AC=BF,∴BF=BD.
在ΔCBF和ΔCBD中,CB=CB,?∠CBF=∠CBD,BF=BD,
∴ΔCBF≌ΔCBD(SAS)·∴CF=CD·∴CD=2CE.
解题策略:
当出现中线,而现有图形中不存在两个全等三角形时,常通过倍长中线法将中线延长一倍,构造全等三角形,再利用对应边相等去寻求线段间的数量关系.利用倍长中线法构造全等三角形
变式练习:
如图,在ΔABC中,AD是边BC上的中线求证:AD<(AB+AC)。
证明:如图,延长AD至点E,使DE=AD,则AE=2AD,连接BE.
∵AD是边BC上的中线,
∴DC=DB.
在ΔACD和ΔEBD中,DC=DB,?∠ADC=∠EDB,AD=ED,?
∴ΔACD≌ΔEBD(SAS).?
∴AC=EB.?
在ΔABE中,AE<AB+EB,
∴2AD
证明:如图,延长AM?至点N,使MN=AM,则NA=2AM,连接BN.
∵M为BC的中点,∴CM=BM.
在ΔAMC和ΔNMB中,AM=NM,?∠AMC=∠NMB,?CM=BM,?
∴ΔAMC≌ΔNMB(SAS),
∴AC=NB,∠C=∠NBM.∴AD=AC,∴AD=BN.
∵AB⊥AE,AD⊥AC,∴∠EAB=∠DAC=90°,
∴∠EAD+∠BAC=360°-∠EAB-∠DAC=180°,
∴∠ABN=∠ABC+∠NBM=∠ABC+∠C=180°-?∠BAC=∠EAD.?
在ΔEAD和ΔABN中,AE=BA,∠EAD=∠ABN,AD=BN,?
.ΔEAD≌ΔABN(SAS),∴DE=NA=2AM.?
基础练习:
如图,AB=AD,AC=AE,添加下列条件,不一定能得到ΔABC≌ΔADE的是(?C
)
A.BC=DE
B.∠BAC=∠DAE
C.∠C=∠E
D.∠BAD=∠CAE
第1题
第2题
第3题
2、如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为?30°
3、如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为??82°?
4、如图,线段AD,CE相交于点B,BC=BD,AB=EB.求证:ΔACD≌ΔEDC.
证明:在ΔABC与ΔEBD中,
AB=BE,∠ABC=∠EBD,BC=BD,
∴ΔABC≌ΔEBD(SAS),?
∴AC=ED,∠A=∠E.AB=EB,BC=BD,
∴.AB+BD=EB+BC,?
即AD=EC.
在ΔACD与ΔEDC中,AC=ED,∠A=∠E,AD=EC,
∴.ΔACD≌ΔEDC(SAS).?
5、如图,在ΔABC中,点D,E,F分别在边BC,AB,AC上,DE=DF,∠EDF=∠B,BE=DC.
(1)求证:BC=FC+BE;
(2)若∠A=100°,求∠EDF的度数.
(1)思路:证ΔBDE≌ΔCFD得到FC=BD∵BE=DC,∴BC=BD+DC=FC+BE
(2)∵ΔBDE≌ΔCFD,∴∠B=∠C.
∵∠A=100°,∴∠B=40°.∴∠EDF=∠B,∴∠EDF=40°.
6、在ΔABC和ΔCDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.
(1)如图1,当α=90°时,求证:①ΔACE≌ΔBCD,②AE⊥BD;
(2)如图2,当α=60°时,求∠AFB的度数;
(3)如图3,直接写出∠AFD的度数为______(用含α的式子表示).
解:思路:(1)证明:证ΔACE≌ΔBCD,∴∠CAE=∠CBD,:∠AFB=∠ACB=90°,∴AE⊥BD;
(2)同(1)可得∠AFB=∠ACB=60°;
(3)同(1)可得∠AFB=∠ACB=α,故∠AFD=180°-α.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
