人教版八上高分笔记之导与练 12.2.3 用ASA或AAS判断三角形全等(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 12.2.3 用ASA或AAS判断三角形全等(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.2全等三角形的判定
用ASA或AAS判定三角形全等
知识要点:
有两角和它们的??
??分别相等的两个三角形全等,简写成??
或??
?
2.有两角和其中??
??分别相等的两个三角形全等,简写成??
或??
?
3.三个角分别相等的两个三角形定?
?全等(填一定或不一定)。
易错点睛:
如图,∠1=∠2,∠3=∠4.求证:AC=AD.
证明:在ΔABD和ΔABC中,
∠1=∠2
AB=AB,
∠3=∠4
∴ΔABD≌ΔABC(ASA),∴AC=AD.
指出上述证明中的错误,并加以改正。
【点睛】易将∠3=∠4作为对应角相等证全等.
典型例题:
题型一
三角形全等的判定与性质的应用
如图,BE,CD相交于点F,∠B=∠C,∠1=∠2,求证:DF=EF.
解题策略
(1)证边相等→两边所在的三角形全等.
(2)已知一边一角(边角相邻),证全等的思路:①找角的另一邻边→“SAS”;②找边相邻的另一角→“ASA”;
③找边的对角→“AAS”.
变式练习:
如图,已知点B,B,C,在一条直线上∠B=∠DEF,BC=BF,现要证明ΔABC≌ΔDEF,若以“SAS”为依据,则还需添加件:?
??;若以“ASA”为依据,则还需添加条件:??
??;若以“AAS”为依据,则还需添加条件:?
第1题
第2题
2、如图,点C,D在AB上,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有(
)
A.2对
B.3对
C.4对
D.5对
3、如图,∠E=∠F=90°,∠B=∠C,AE=AF.请你判断ΔACN≌ΔABM是否成立,并说明理由.
题型二
利用全等三角形解决实际问题
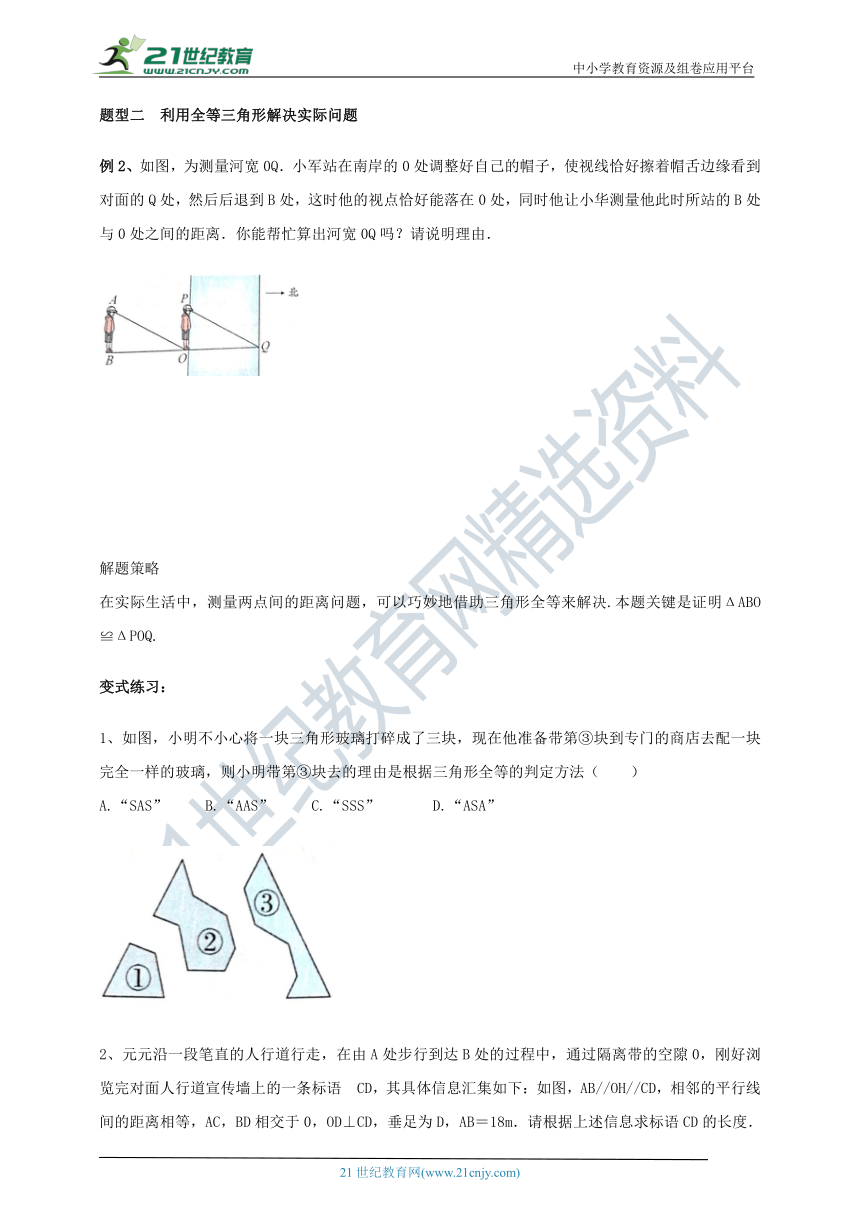
例2、如图,为测量河宽0Q.小军站在南岸的0处调整好自己的帽子,使视线恰好擦着帽舌边缘看到对面的Q处,然后后退到B处,这时他的视点恰好能落在0处,同时他让小华测量他此时所站的B处与0处之间的距离.你能帮忙算出河宽0Q吗?请说明理由.
解题策略
在实际生活中,测量两点间的距离问题,可以巧妙地借助三角形全等来解决.本题关键是证明ΔABO≌ΔPOQ.?
变式练习:
1、如图,小明不小心将一块三角形玻璃打碎成了三块,现在他准备带第③块到专门的商店去配一块完全一样的玻璃,则小明带第③块去的理由是根据三角形全等的判定方法(
)
A.“SAS”
B.“AAS”
C.“SSS”
D.“ASA”
2、元元沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙0,刚好浏览完对面人行道宣传墙上的一条标语?CD,其具体信息汇集如下:如图,AB//OH//CD,相邻的平行线间的距离相等,AC,BD相交于0,OD⊥CD,垂足为D,AB=18m.请根据上述信息求标语CD的长度.
题型三
利用截长补短法构造全等三角形
例3、如图,E为AD上A一点,AB/CD、BE平分<ABG,CE平分<BCD.求证:BC=AB+CD.?
解题策略:证明一条线段的长度等于两条线段的长度的和(或差)时,常用截长补短法,证明思路一般是:(1)截长,即在较长线段上截取一段,使之等于其中一条较短线段的长,然后证明剩下的线段长等于另一条较短线段的长;(2)补短,即将其中的一条较短线段直接延长至等于较长线段的长,然后证明延长部分线段的长等于另一条较短线段的长(或延长其中一条较短线段,使延长部分线段的长等于另一条较短线段的长,然后证明延长后的线段长等于较长线段的长).
变式练习:
1、如图,在ΔABC中,∠B=2∠C,AD⊥BC于点D.求证:CD=AB+BD.
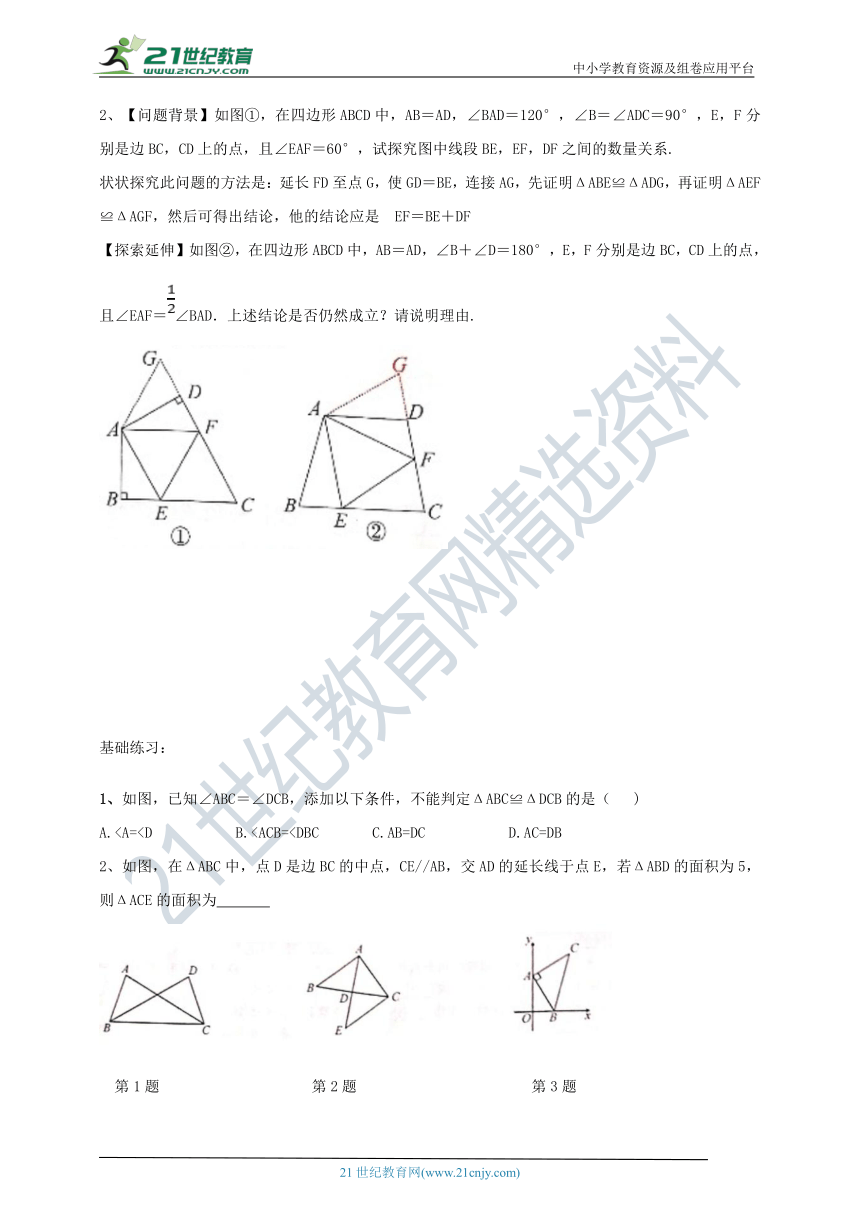
2、【问题背景】如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是边BC,CD上的点,且∠EAF=60°,试探究图中线段BE,EF,DF之间的数量关系.
状状探究此问题的方法是:延长FD至点G,使GD=BE,连接AG,先证明ΔABE≌ΔADG,再证明ΔAEF≌ΔAGF,然后可得出结论,他的结论应是?EF=BE+DF
【探索延伸】如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.上述结论是否仍然成立?请说明理由.
基础练习:
如图,已知∠ABC=∠DCB,添加以下条件,不能判定ΔABC≌ΔDCB的是(?
)
A.?B.?C.AB=DC???
??D.AC=DB
2、如图,在ΔABC中,点D是边BC的中点,CE//AB,交AD的延长线于点E,若ΔABD的面积为5,则ΔACE的面积为??
第1题
第2题
第3题
3、如图,A(0,3),B(2,0),AC=AB,AC」AB,则点C的坐标为??________
4、如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,AC=CE.求证:BD=AB+DE.?
5、如图,锐角ΔABC的高AD,BE交于点F,若BF=AC,BC=9,CD=3.求AF的长.
综合题探究
6、【问题背景】(1)如图1,在RtΔABC中,AC=BC,∠ACB=90°,∠ADC=90°,BE⊥CD,
垂足为E.求证:CD=BE;
【变式运用】(2)如图2,在RtΔABC中,AC=BC,∠ACB=∠CDA=90°,CD=2.求SΔBDC;
【拓展迁移】(3)如图3,在RtΔABC中,AC=BC,∠ACB=∠ADC=90°,CD与AB交于点E,AD=1,BE=4AE,直接写出求SΔBDC.
答案:
知识要点:
有两角和它们的??夹边??分别相等的两个三角形全等,简写成??角边角或??ASA?
2.有两角和其中??一角的对边??分别相等的两个三角形全等,简写成??角角边或??AAS?
3.三个角分别相等的两个三角形定?不一定?全等(填一定或不一定)。
易错点睛:
如图,∠1=∠2,∠3=∠4.求证:AC=AD.
证明:在ΔABD和ΔABC中,
∠1=∠2
AB=AB,
∠3=∠4
∴ΔABD≌ΔABC(ASA),∴AC=AD.
指出上述证明中的错误,并加以改正。
【点睛】易将∠3=∠4作为对应角相等证全等.
正确解:解答:证明:∵∠3=∠4,
∴∠ABD=∠ABC(等角的补角相等),
在△ABD与△ABC中,
,
∴△ADB≌△ACB(ASA),
∴AC=AD.
典型例题:
题型一
三角形全等的判定与性质的应用
如图,BE,CD相交于点F,∠B=∠C,∠1=∠2,求证:DF=EF.
证明:∵∠1=∠2,∠C=∠B,
∴∠1-∠C=∠2-∠B,即∠CAF=∠BAF.
在ΔADF和ΔAEF中,∠DAF=∠EAF,?AF=AF,?∠1=∠2,?
∴ΔADF≌ΔAEF(ASA).
∴DF=EF.
解题策略
(1)证边相等→两边所在的三角形全等.
(2)已知一边一角(边角相邻),证全等的思路:①找角的另一邻边→“SAS”;②找边相邻的另一角→“ASA”;
③找边的对角→“AAS”.
变式练习:
如图,已知点B,B,C,在一条直线上∠B=∠DEF,BC=BF,现要证明ΔABC
ΔDEF,若以“SAS”为依据,则还需添加件:?AB=DE??;若以“ASA”为依据,则还需添加条件:??∠ACB=∠F??;若以“AAS”为依据,则还需添加条件:?∠A=∠D
第1题
第2题
2、如图,点C,D在AB上,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有(B)
A.2对
B.3对
C.4对
D.5对
3、如图,∠E=∠F=90°,∠B=∠C,AE=AF.请你判断ΔACN≌ΔABM是否成立,并说明理由.
解:成立,理由如下:
在ΔAEB和ΔAFC中,
∠B=∠C,
∠E=∠F
AE=AF,
∴ΔAEB≌ΔAFC(AAS)∴AB=AC.
在ΔACN和ΔABM中,?AC=AB,?∠B=∠C,?∠CAN=∠BAM,?
∴ΔACN≌ΔABM(ASA).?
题型二
利用全等三角形解决实际问题
例2、如图,为测量河宽0Q.小军站在南岸的0处调整好自己的帽子,使视线恰好擦着帽舌边缘看到对面的Q处,然后后退到B处,这时他的视点恰好能落在0处,同时他让小华测量他此时所站的B处与0处之间的距离.你能帮忙算出河宽0Q吗?请说明理由.
解:根据题意知AB=PO,∠A=∠OPQ.
∵AB⊥BO,PO⊥BQ,∴∠B=∠POQ=90°.
在ΔABO和ΔPOQ中,∠A=∠OPQ,?AB=PO,∠B=∠POQ,
∴ΔABO≌ΔPOQ(ASA).
∴BO=0Q,即河宽0Q为所测量的BO的长度.
解题策略
在实际生活中,测量两点间的距离问题,可以巧妙地借助三角形全等来解决.本题关键是证明ΔABO≌ΔPOQ.?
变式练习:
1、如图,小明不小心将一块三角形玻璃打碎成了三块,现在他准备带第③块到专门的商店去配一块完全一样的玻璃,则小明带第③块去的理由是根据三角形全等的判定方法(
D
)
A.“SAS”
B.“AAS”
C.“SSS”
D.“ASA”
2、元元沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙0,刚好浏览完对面人行道宣传墙上的一条标语?CD,其具体信息汇集如下:如图,AB//OH//CD,相邻的平行线间的距离相等,AC,BD相交于0,OD⊥CD,垂足为D,AB=18m.请根据上述信息求标语CD的长度.
解:AB//CD,∴∠ABO=∠CDO.
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,∴OB⊥AB.
∵相邻的两平行线间的距离相等,∴OD=OB.
在ΔABO和ΔCDO中,∠ABO=∠CDO,?OB=OD,∠AOB=∠COD,
∴ΔABO≌ΔCDO(ASA),
∴AB=CD=18m,即标语CD的长度为18m.
题型三
利用截长补短法构造全等三角形
例3、如图,E为AD上A一点,AB/CD、BE平分<ABG,CE平分<BCD.求证:BC=AB+CD.?
证明:
证法1(截长法):如图①,在BC上取点F,使BF=
BA,连接EF.
BE平分∠ABC,CE平分∠BCD,
∴∠1=∠2,∠3=∠4.
在ΔABE和ΔFBE中,BA=BF,???∠1=∠2,?BE=BE,?
∴ΔABE≌ΔFBE(SAS)∴∠A=∠5.
∴AB//CD,∴∠A+∠D=180°.
∴∠5+∠6=180°,∴∠6=∠D.
在ΔEFC和ΔEDC中,∠6=∠D,?<3=<4,?EC=EC,?
∴ΔEFC≌ΔEDC(AAS)∴CF=CD.
∴BC=BF+CF=AB+CD.
证法2(补短法):如图②,延长BA至点F,使BF=BC,连接EF.
∵BE平分∠ABC,CE平分∠BCD,
∴∠1=∠2,∠3=∠4.
在ΔBEF和ΔBEC中,BF=BC,?∠1=∠2,?BE=BE,?
∴ΔBEF≌ΔBEC(SAS).∴∠F=∠3,EF=EC.
∵∠3=∠4,∴∠F=∠4.
∵AB//CD,∴∠5=∠D.
在ΔAEF和ΔDEC中,∠5=∠D,∠F=∠4,EF=EC,?
∴ΔAEF≌ΔDEC(AAS)∴AF=DC.
∴BC=BF=AB+AF=AB+CD.
解题策略:证明一条线段的长度等于两条线段的长度的和(或差)时,常用截长补短法,证明思路一般是:(1)截长,即在较长线段上截取一段,使之等于其中一条较短线段的长,然后证明剩下的线段长等于另一条较短线段的长;(2)补短,即将其中的一条较短线段直接延长至等于较长线段的长,然后证明延长部分线段的长等于另一条较短线段的长(或延长其中一条较短线段,使延长部分线段的长等于另一条较短线段的长,然后证明延长后的线段长等于较长线段的长).
变式练习:
1、如图,在ΔABC中,∠B=2∠C,AD⊥BC于点D.求证:CD=AB+BD.
证明:如图,在CD上截取DE=DB,连接AE,过点E作EFLAC于点F.
∵AD⊥BC,∴∠ADB=∠ADE=90°.
在ΔADB和ΔADE中,AD=AD,?∠ADB=∠ADE,?DB=DE,?
∴ΔADB≌ΔADE(SAS).?
∴AB=AE,∠B=∠AED.?
∵∠B=2∠C,∴∠AED=2∠C.?
又∠AED=∠C+∠CAE,
∴∠C=∠CAE.?
∵EF⊥AC,∴∠CFE=∠AFE=90°.?
在ΔCFE和ΔAFE中,∠C=∠FAE,?∠CFE=∠AFE,?EF=EF,?
∴ΔCFE≌ΔAFE(AAS)∴CE=AE.
∴CE=AB.又CD=CE+DE,∴CD=AB+BD.
【问题背景】如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是边BC,CD上的点,且∠EAF=60°,试探究图中线段BE,EF,DF之间的数量关系.
状状探究此问题的方法是:延长FD至点G,使GD=BE,连接AG,先证明ΔABE≌ΔADG,再证明ΔAEF≌ΔAGF,然后可得出结论,他的结论应是?EF=BE+DF
【探索延伸】如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.上述结论是否仍然成立?请说明理由.
解:结论EF=BE+DF仍然成立,理由:
如图②,延长FD至点G,使DG=BE,连接AG.
∵∠B+∠ADF=180°,∠ADG+∠ADF=?180°,∴∠B=∠ADG.?
在ΔABE和ΔADG中
BE=DG,??∠B=∠ADG,?AB=AD,?
∴ΔABE≌ΔADG(SAS),
∴AE=AG,∠BAE=∠DAG.
∴∠EAF=∠BAD,
∴∠EAF=∠BAE+∠DAF,
∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=?∠EAF.??
在ΔAEF和ΔAGF中,AE=AG,?∠EAF=∠GAF?AF=AF,?
∴ΔAEF≌ΔAGF(SAS),∴EF=GF.?
∵GF=DG+DF∴EF=BE+DF.
基础练习:
如图,已知∠ABC=∠DCB,添加以下条件,不能判定ΔABC≌ΔDCB的是(?D
)
A.?B.?C.AB=DC???
??D.AC=DB
2、如图,在ΔABC中,点D是边BC的中点,CE//AB,交AD的延长线于点E,若ΔABD的面积为5,则ΔACE的面积为??10
第1题
第2题
第3题
3、如图,A(0,3),B(2,0),AC=AB,AC」AB,则点C的坐标为??(3.5)
4、如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,AC=CE.求证:BD=AB+DE.?
证明:∵AB⊥BD,ED⊥BD.AC⊥CE,∴∠ACE=∠ABC=∠CDE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,∠ACB=∠CED.
在ΔABC和ΔCDE中,∠ACB=∠CED,?∠B=∠D,?AC=EC,????
ΔABC≌ΔCDE(AAS).
∴BC=DE.AB=CD.ABD=CD+BC=AB+DE.
如图,锐角ΔABC的高AD,BE交于点F,若BF=AC,BC=9,CD=3.求AF的长.
解:∵AD⊥BC,BE⊥AC,∴∠ADB=∠ADC=∠BEC=90°.
∴∠EBC+∠C=90°,∠DAC+∠C=90°.∠EBC=∠DAC.
在ΔFBD与ΔCAD中,∠DAC=∠FBD,?∠ADC=∠ADB,AC=BF,∴.ΔCAD≌ΔFBD(AAS).
∴FD=DC=3,BD=AD.∵BC=6,∴AD=BD=BC-CD=6.∴AF=AD-FD=6-3=3.
综合题探究
6、【问题背景】(1)如图1,在RtΔABC中,AC=BC,∠ACB=90°,∠ADC=90°,BE⊥CD,
垂足为E.求证:CD=BE;
【变式运用】(2)如图2,在RtΔABC中,AC=BC,∠ACB=∠CDA=90°,CD=2.求SΔBDC;
【拓展迁移】(3)如图3,在RtΔABC中,AC=BC,∠ACB=∠ADC=90°,CD与AB交于点E,AD=1,BE=4AE,直接写出求SΔBDC.
解:(1)∵∠ACB=∠ADC=90°,BE⊥CD,
∴∠ADC=∠CEB=90°,∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,?
在ΔACD与ΔCBE中,∠ACD=∠CBE,∠ADC=∠CEB,AC=BC,
∴ΔACD≌ΔCBE(AAS).∴CD=BE;?
(2)过点B作BE⊥CD,垂足为E,:AC=BC,∠ACB=∠ADC=90°,由(1)知,BE=CD=2..SΔBDC=CD·BE=2;?
(3)过点B作BF⊥CD,垂足为F,∵AC=BC,∠ACB=∠ADC=90°,
∴由(1)知BF=CD.==
∵BE=4AE,∴BF=4AD=4,CD=BF=4,.SΔBDC=CD·BF=8.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2全等三角形的判定
用ASA或AAS判定三角形全等
知识要点:
有两角和它们的??
??分别相等的两个三角形全等,简写成??
或??
?
2.有两角和其中??
??分别相等的两个三角形全等,简写成??
或??
?
3.三个角分别相等的两个三角形定?
?全等(填一定或不一定)。
易错点睛:
如图,∠1=∠2,∠3=∠4.求证:AC=AD.
证明:在ΔABD和ΔABC中,
∠1=∠2
AB=AB,
∠3=∠4
∴ΔABD≌ΔABC(ASA),∴AC=AD.
指出上述证明中的错误,并加以改正。
【点睛】易将∠3=∠4作为对应角相等证全等.
典型例题:
题型一
三角形全等的判定与性质的应用
如图,BE,CD相交于点F,∠B=∠C,∠1=∠2,求证:DF=EF.
解题策略
(1)证边相等→两边所在的三角形全等.
(2)已知一边一角(边角相邻),证全等的思路:①找角的另一邻边→“SAS”;②找边相邻的另一角→“ASA”;
③找边的对角→“AAS”.
变式练习:
如图,已知点B,B,C,在一条直线上∠B=∠DEF,BC=BF,现要证明ΔABC≌ΔDEF,若以“SAS”为依据,则还需添加件:?
??;若以“ASA”为依据,则还需添加条件:??
??;若以“AAS”为依据,则还需添加条件:?
第1题
第2题
2、如图,点C,D在AB上,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有(
)
A.2对
B.3对
C.4对
D.5对
3、如图,∠E=∠F=90°,∠B=∠C,AE=AF.请你判断ΔACN≌ΔABM是否成立,并说明理由.
题型二
利用全等三角形解决实际问题
例2、如图,为测量河宽0Q.小军站在南岸的0处调整好自己的帽子,使视线恰好擦着帽舌边缘看到对面的Q处,然后后退到B处,这时他的视点恰好能落在0处,同时他让小华测量他此时所站的B处与0处之间的距离.你能帮忙算出河宽0Q吗?请说明理由.
解题策略
在实际生活中,测量两点间的距离问题,可以巧妙地借助三角形全等来解决.本题关键是证明ΔABO≌ΔPOQ.?
变式练习:
1、如图,小明不小心将一块三角形玻璃打碎成了三块,现在他准备带第③块到专门的商店去配一块完全一样的玻璃,则小明带第③块去的理由是根据三角形全等的判定方法(
)
A.“SAS”
B.“AAS”
C.“SSS”
D.“ASA”
2、元元沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙0,刚好浏览完对面人行道宣传墙上的一条标语?CD,其具体信息汇集如下:如图,AB//OH//CD,相邻的平行线间的距离相等,AC,BD相交于0,OD⊥CD,垂足为D,AB=18m.请根据上述信息求标语CD的长度.
题型三
利用截长补短法构造全等三角形
例3、如图,E为AD上A一点,AB/CD、BE平分<ABG,CE平分<BCD.求证:BC=AB+CD.?
解题策略:证明一条线段的长度等于两条线段的长度的和(或差)时,常用截长补短法,证明思路一般是:(1)截长,即在较长线段上截取一段,使之等于其中一条较短线段的长,然后证明剩下的线段长等于另一条较短线段的长;(2)补短,即将其中的一条较短线段直接延长至等于较长线段的长,然后证明延长部分线段的长等于另一条较短线段的长(或延长其中一条较短线段,使延长部分线段的长等于另一条较短线段的长,然后证明延长后的线段长等于较长线段的长).
变式练习:
1、如图,在ΔABC中,∠B=2∠C,AD⊥BC于点D.求证:CD=AB+BD.
2、【问题背景】如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是边BC,CD上的点,且∠EAF=60°,试探究图中线段BE,EF,DF之间的数量关系.
状状探究此问题的方法是:延长FD至点G,使GD=BE,连接AG,先证明ΔABE≌ΔADG,再证明ΔAEF≌ΔAGF,然后可得出结论,他的结论应是?EF=BE+DF
【探索延伸】如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.上述结论是否仍然成立?请说明理由.
基础练习:
如图,已知∠ABC=∠DCB,添加以下条件,不能判定ΔABC≌ΔDCB的是(?
)
A.
??D.AC=DB
2、如图,在ΔABC中,点D是边BC的中点,CE//AB,交AD的延长线于点E,若ΔABD的面积为5,则ΔACE的面积为??
第1题
第2题
第3题
3、如图,A(0,3),B(2,0),AC=AB,AC」AB,则点C的坐标为??________
4、如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,AC=CE.求证:BD=AB+DE.?
5、如图,锐角ΔABC的高AD,BE交于点F,若BF=AC,BC=9,CD=3.求AF的长.
综合题探究
6、【问题背景】(1)如图1,在RtΔABC中,AC=BC,∠ACB=90°,∠ADC=90°,BE⊥CD,
垂足为E.求证:CD=BE;
【变式运用】(2)如图2,在RtΔABC中,AC=BC,∠ACB=∠CDA=90°,CD=2.求SΔBDC;
【拓展迁移】(3)如图3,在RtΔABC中,AC=BC,∠ACB=∠ADC=90°,CD与AB交于点E,AD=1,BE=4AE,直接写出求SΔBDC.
答案:
知识要点:
有两角和它们的??夹边??分别相等的两个三角形全等,简写成??角边角或??ASA?
2.有两角和其中??一角的对边??分别相等的两个三角形全等,简写成??角角边或??AAS?
3.三个角分别相等的两个三角形定?不一定?全等(填一定或不一定)。
易错点睛:
如图,∠1=∠2,∠3=∠4.求证:AC=AD.
证明:在ΔABD和ΔABC中,
∠1=∠2
AB=AB,
∠3=∠4
∴ΔABD≌ΔABC(ASA),∴AC=AD.
指出上述证明中的错误,并加以改正。
【点睛】易将∠3=∠4作为对应角相等证全等.
正确解:解答:证明:∵∠3=∠4,
∴∠ABD=∠ABC(等角的补角相等),
在△ABD与△ABC中,
,
∴△ADB≌△ACB(ASA),
∴AC=AD.
典型例题:
题型一
三角形全等的判定与性质的应用
如图,BE,CD相交于点F,∠B=∠C,∠1=∠2,求证:DF=EF.
证明:∵∠1=∠2,∠C=∠B,
∴∠1-∠C=∠2-∠B,即∠CAF=∠BAF.
在ΔADF和ΔAEF中,∠DAF=∠EAF,?AF=AF,?∠1=∠2,?
∴ΔADF≌ΔAEF(ASA).
∴DF=EF.
解题策略
(1)证边相等→两边所在的三角形全等.
(2)已知一边一角(边角相邻),证全等的思路:①找角的另一邻边→“SAS”;②找边相邻的另一角→“ASA”;
③找边的对角→“AAS”.
变式练习:
如图,已知点B,B,C,在一条直线上∠B=∠DEF,BC=BF,现要证明ΔABC
ΔDEF,若以“SAS”为依据,则还需添加件:?AB=DE??;若以“ASA”为依据,则还需添加条件:??∠ACB=∠F??;若以“AAS”为依据,则还需添加条件:?∠A=∠D
第1题
第2题
2、如图,点C,D在AB上,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有(B)
A.2对
B.3对
C.4对
D.5对
3、如图,∠E=∠F=90°,∠B=∠C,AE=AF.请你判断ΔACN≌ΔABM是否成立,并说明理由.
解:成立,理由如下:
在ΔAEB和ΔAFC中,
∠B=∠C,
∠E=∠F
AE=AF,
∴ΔAEB≌ΔAFC(AAS)∴AB=AC.
在ΔACN和ΔABM中,?AC=AB,?∠B=∠C,?∠CAN=∠BAM,?
∴ΔACN≌ΔABM(ASA).?
题型二
利用全等三角形解决实际问题
例2、如图,为测量河宽0Q.小军站在南岸的0处调整好自己的帽子,使视线恰好擦着帽舌边缘看到对面的Q处,然后后退到B处,这时他的视点恰好能落在0处,同时他让小华测量他此时所站的B处与0处之间的距离.你能帮忙算出河宽0Q吗?请说明理由.
解:根据题意知AB=PO,∠A=∠OPQ.
∵AB⊥BO,PO⊥BQ,∴∠B=∠POQ=90°.
在ΔABO和ΔPOQ中,∠A=∠OPQ,?AB=PO,∠B=∠POQ,
∴ΔABO≌ΔPOQ(ASA).
∴BO=0Q,即河宽0Q为所测量的BO的长度.
解题策略
在实际生活中,测量两点间的距离问题,可以巧妙地借助三角形全等来解决.本题关键是证明ΔABO≌ΔPOQ.?
变式练习:
1、如图,小明不小心将一块三角形玻璃打碎成了三块,现在他准备带第③块到专门的商店去配一块完全一样的玻璃,则小明带第③块去的理由是根据三角形全等的判定方法(
D
)
A.“SAS”
B.“AAS”
C.“SSS”
D.“ASA”
2、元元沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙0,刚好浏览完对面人行道宣传墙上的一条标语?CD,其具体信息汇集如下:如图,AB//OH//CD,相邻的平行线间的距离相等,AC,BD相交于0,OD⊥CD,垂足为D,AB=18m.请根据上述信息求标语CD的长度.
解:AB//CD,∴∠ABO=∠CDO.
∵OD⊥CD,∴∠CDO=90°,
∴∠ABO=90°,∴OB⊥AB.
∵相邻的两平行线间的距离相等,∴OD=OB.
在ΔABO和ΔCDO中,∠ABO=∠CDO,?OB=OD,∠AOB=∠COD,
∴ΔABO≌ΔCDO(ASA),
∴AB=CD=18m,即标语CD的长度为18m.
题型三
利用截长补短法构造全等三角形
例3、如图,E为AD上A一点,AB/CD、BE平分<ABG,CE平分<BCD.求证:BC=AB+CD.?
证明:
证法1(截长法):如图①,在BC上取点F,使BF=
BA,连接EF.
BE平分∠ABC,CE平分∠BCD,
∴∠1=∠2,∠3=∠4.
在ΔABE和ΔFBE中,BA=BF,???∠1=∠2,?BE=BE,?
∴ΔABE≌ΔFBE(SAS)∴∠A=∠5.
∴AB//CD,∴∠A+∠D=180°.
∴∠5+∠6=180°,∴∠6=∠D.
在ΔEFC和ΔEDC中,∠6=∠D,?<3=<4,?EC=EC,?
∴ΔEFC≌ΔEDC(AAS)∴CF=CD.
∴BC=BF+CF=AB+CD.
证法2(补短法):如图②,延长BA至点F,使BF=BC,连接EF.
∵BE平分∠ABC,CE平分∠BCD,
∴∠1=∠2,∠3=∠4.
在ΔBEF和ΔBEC中,BF=BC,?∠1=∠2,?BE=BE,?
∴ΔBEF≌ΔBEC(SAS).∴∠F=∠3,EF=EC.
∵∠3=∠4,∴∠F=∠4.
∵AB//CD,∴∠5=∠D.
在ΔAEF和ΔDEC中,∠5=∠D,∠F=∠4,EF=EC,?
∴ΔAEF≌ΔDEC(AAS)∴AF=DC.
∴BC=BF=AB+AF=AB+CD.
解题策略:证明一条线段的长度等于两条线段的长度的和(或差)时,常用截长补短法,证明思路一般是:(1)截长,即在较长线段上截取一段,使之等于其中一条较短线段的长,然后证明剩下的线段长等于另一条较短线段的长;(2)补短,即将其中的一条较短线段直接延长至等于较长线段的长,然后证明延长部分线段的长等于另一条较短线段的长(或延长其中一条较短线段,使延长部分线段的长等于另一条较短线段的长,然后证明延长后的线段长等于较长线段的长).
变式练习:
1、如图,在ΔABC中,∠B=2∠C,AD⊥BC于点D.求证:CD=AB+BD.
证明:如图,在CD上截取DE=DB,连接AE,过点E作EFLAC于点F.
∵AD⊥BC,∴∠ADB=∠ADE=90°.
在ΔADB和ΔADE中,AD=AD,?∠ADB=∠ADE,?DB=DE,?
∴ΔADB≌ΔADE(SAS).?
∴AB=AE,∠B=∠AED.?
∵∠B=2∠C,∴∠AED=2∠C.?
又∠AED=∠C+∠CAE,
∴∠C=∠CAE.?
∵EF⊥AC,∴∠CFE=∠AFE=90°.?
在ΔCFE和ΔAFE中,∠C=∠FAE,?∠CFE=∠AFE,?EF=EF,?
∴ΔCFE≌ΔAFE(AAS)∴CE=AE.
∴CE=AB.又CD=CE+DE,∴CD=AB+BD.
【问题背景】如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是边BC,CD上的点,且∠EAF=60°,试探究图中线段BE,EF,DF之间的数量关系.
状状探究此问题的方法是:延长FD至点G,使GD=BE,连接AG,先证明ΔABE≌ΔADG,再证明ΔAEF≌ΔAGF,然后可得出结论,他的结论应是?EF=BE+DF
【探索延伸】如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.上述结论是否仍然成立?请说明理由.
解:结论EF=BE+DF仍然成立,理由:
如图②,延长FD至点G,使DG=BE,连接AG.
∵∠B+∠ADF=180°,∠ADG+∠ADF=?180°,∴∠B=∠ADG.?
在ΔABE和ΔADG中
BE=DG,??∠B=∠ADG,?AB=AD,?
∴ΔABE≌ΔADG(SAS),
∴AE=AG,∠BAE=∠DAG.
∴∠EAF=∠BAD,
∴∠EAF=∠BAE+∠DAF,
∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=?∠EAF.??
在ΔAEF和ΔAGF中,AE=AG,?∠EAF=∠GAF?AF=AF,?
∴ΔAEF≌ΔAGF(SAS),∴EF=GF.?
∵GF=DG+DF∴EF=BE+DF.
基础练习:
如图,已知∠ABC=∠DCB,添加以下条件,不能判定ΔABC≌ΔDCB的是(?D
)
A.
??D.AC=DB
2、如图,在ΔABC中,点D是边BC的中点,CE//AB,交AD的延长线于点E,若ΔABD的面积为5,则ΔACE的面积为??10
第1题
第2题
第3题
3、如图,A(0,3),B(2,0),AC=AB,AC」AB,则点C的坐标为??(3.5)
4、如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,AC=CE.求证:BD=AB+DE.?
证明:∵AB⊥BD,ED⊥BD.AC⊥CE,∴∠ACE=∠ABC=∠CDE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,∠ACB=∠CED.
在ΔABC和ΔCDE中,∠ACB=∠CED,?∠B=∠D,?AC=EC,????
ΔABC≌ΔCDE(AAS).
∴BC=DE.AB=CD.ABD=CD+BC=AB+DE.
如图,锐角ΔABC的高AD,BE交于点F,若BF=AC,BC=9,CD=3.求AF的长.
解:∵AD⊥BC,BE⊥AC,∴∠ADB=∠ADC=∠BEC=90°.
∴∠EBC+∠C=90°,∠DAC+∠C=90°.∠EBC=∠DAC.
在ΔFBD与ΔCAD中,∠DAC=∠FBD,?∠ADC=∠ADB,AC=BF,∴.ΔCAD≌ΔFBD(AAS).
∴FD=DC=3,BD=AD.∵BC=6,∴AD=BD=BC-CD=6.∴AF=AD-FD=6-3=3.
综合题探究
6、【问题背景】(1)如图1,在RtΔABC中,AC=BC,∠ACB=90°,∠ADC=90°,BE⊥CD,
垂足为E.求证:CD=BE;
【变式运用】(2)如图2,在RtΔABC中,AC=BC,∠ACB=∠CDA=90°,CD=2.求SΔBDC;
【拓展迁移】(3)如图3,在RtΔABC中,AC=BC,∠ACB=∠ADC=90°,CD与AB交于点E,AD=1,BE=4AE,直接写出求SΔBDC.
解:(1)∵∠ACB=∠ADC=90°,BE⊥CD,
∴∠ADC=∠CEB=90°,∠ACD+∠BCE=90°,∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,?
在ΔACD与ΔCBE中,∠ACD=∠CBE,∠ADC=∠CEB,AC=BC,
∴ΔACD≌ΔCBE(AAS).∴CD=BE;?
(2)过点B作BE⊥CD,垂足为E,:AC=BC,∠ACB=∠ADC=90°,由(1)知,BE=CD=2..SΔBDC=CD·BE=2;?
(3)过点B作BF⊥CD,垂足为F,∵AC=BC,∠ACB=∠ADC=90°,
∴由(1)知BF=CD.==
∵BE=4AE,∴BF=4AD=4,CD=BF=4,.SΔBDC=CD·BF=8.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
