24.1.4圆周角

(共35张PPT)
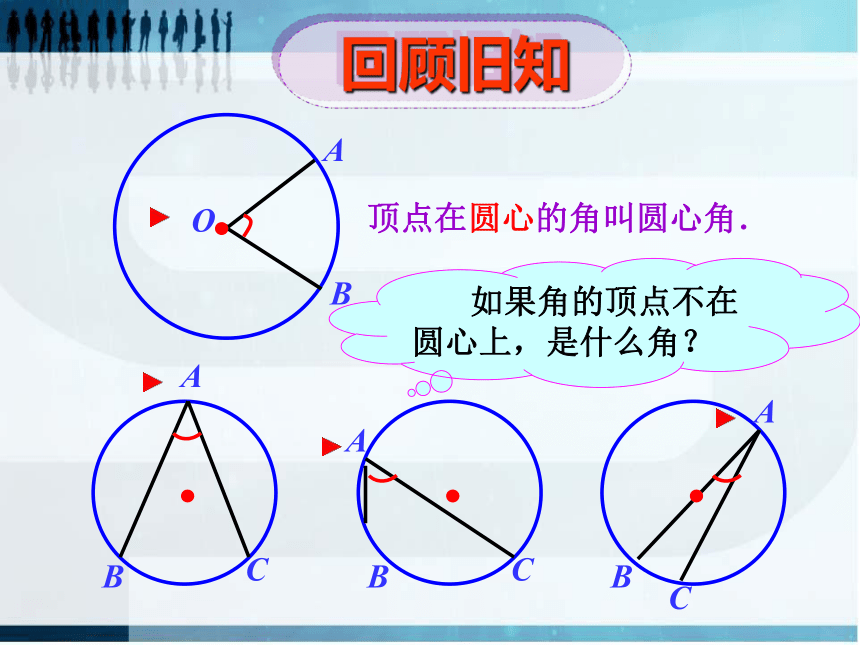
顶点在圆心的角叫圆心角．
·
O
B
A
回顾旧知
A
B
C
A
B
C
A
B
C
如果角的顶点不在圆心上，是什么角？
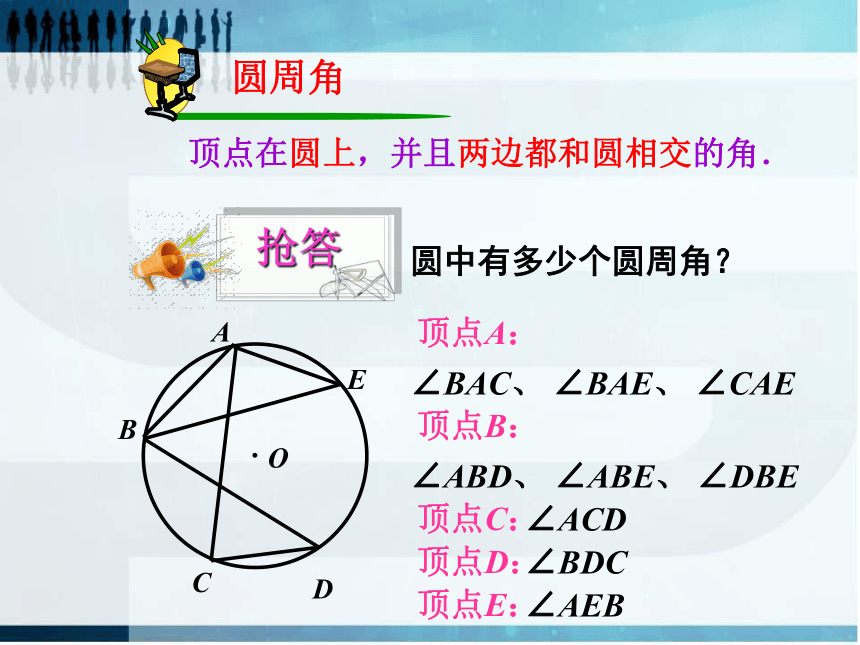
顶点在圆上，并且两边都和圆相交的角．
圆周角
·
E
D
B
A
C
O
抢答
圆中有多少个圆周角？
顶点A：
∠BAC、 ∠BAE、 ∠CAE
顶点B：
∠ABD、 ∠ABE、 ∠DBE
顶点C：
∠ACD
顶点D：
顶点E：
∠BDC
∠AEB
教学目标
【知识与能力】
理解圆周角的概念．
掌握圆周角的两个特征、定理的内容及简单应用．
继续培养学生观察、分析、想象、归纳和逻辑推理的能力．
【过程与方法】
【情感态度与价值观】
渗透由“特殊到一般”，由“一般到特殊”的数学思想方法．
教学重难点
圆周角的概念和圆周角定理．
圆周角定理的证明中由“一般到特殊”的数学思想方法和完全归纳法的数学思想．
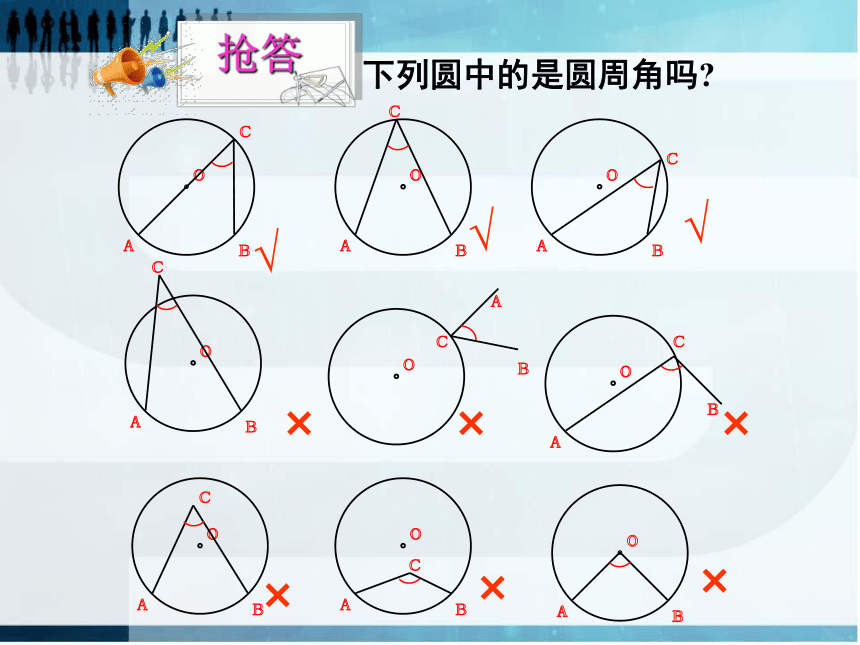
下列圆中的是圆周角吗
抢答
√
×
√
×
√
×
×
×
×
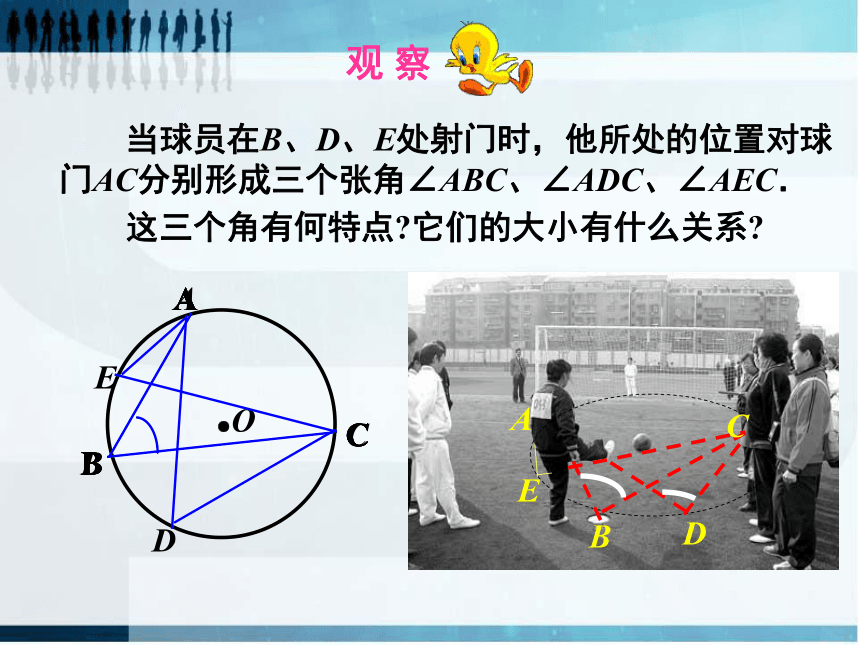
当球员在B、D、E处射门时，他所处的位置对球门AC分别形成三个张角∠ABC、∠ADC、∠AEC．
这三个角有何特点 它们的大小有什么关系
●O
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
D
E
D
E
观 察
·
C
E
B
A
D
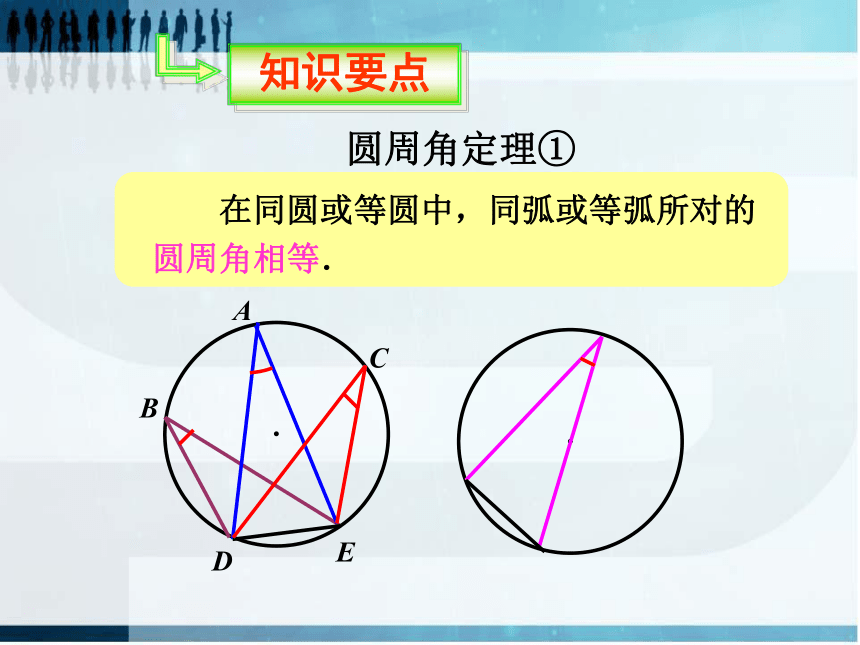
知识要点
在同圆或等圆中，同弧或等弧所对的圆周角相等．
·
圆周角定理①
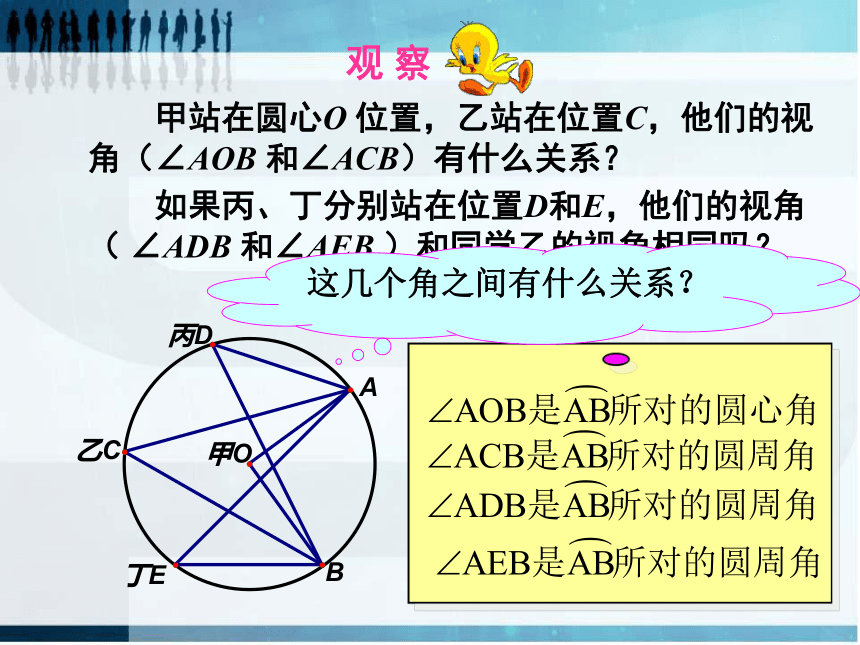
甲站在圆心O 位置，乙站在位置C，他们的视角（∠AOB 和∠ACB）有什么关系？
如果丙、丁分别站在位置D和E，他们的视角（ ∠ADB 和∠AEB ）和同学乙的视角相同吗？
观 察
这几个角之间有什么关系？
类比圆心角推导圆周角的性质
在同圆或等圆中，同弧或等弧所对的 圆心角 相等．
圆周角
结论是否成立？
回顾
举一反三
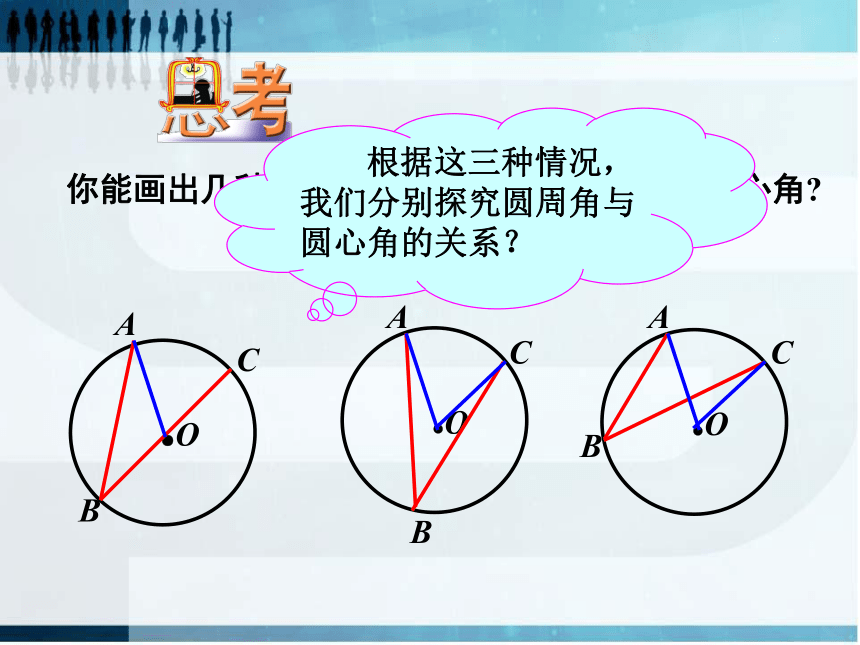
你能画出几种同弧（等弧）所对的圆周角和圆心角
●O
A
B
C
●O
A
B
C
●O
A
B
C
根据这三种情况，我们分别探究圆周角与圆心角的关系？
探究
将圆对折，使折痕经过圆心O和∠BAC的顶点A．
·
C
O
A
B
即
∵OA=OC，
∴∠A=∠C．
又∠BOC=∠A＋∠C
∴∠BOC=2∠A
（1）折痕在圆周角的一条边上．
圆周角与圆心角的关系
（2）折痕在圆周角的内部．
作直径AD，
利用（1）的结果，有
·
C
O
A
B
D
探究
将圆对折，使折痕经过圆心O和∠BAC的顶点A．
圆周角与圆心角的关系
（3）折痕在圆周角的外部．
·
C
O
A
B
D
作直径AD，
利用（1）的结果，有
探究
将圆对折，使折痕经过圆心O和∠BAC的顶点A．
圆周角与圆心角的关系
·
A
B
C1
O
C2
C3
圆周角等于这条弧所对的圆心角的一半．
半圆（或直径）所对的圆周角是直角;
90°的圆周角所对的弦是直径．
知识要点
圆周角定理②
圆周角定理的推论
┓
┓
┓
⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．
又在Rt△ABD中，AD2+BD2=AB2，
·
A
B
C
D
O
解：∵AB是直径，
∴ ∠ACB= ∠ADB=90°．
在Rt△ABC中，
∵CD平分∠ACB，
∴AD=BD．
10
6
）
）
8
例题
·
A
B
C
O
求证： △ABC 为直角三角形．
证明：
CO= AB，
以AB为直径作⊙O，
∵AO=BO，
∴AO=BO=CO．
∴点C在⊙O上．
又∵AB为直径，
∴∠ACB= ×180°= 90°．
已知：△ABC 中，CO为AB边上的中线，
且CO= AB
∴ △ABC 为直角三角形．
例题
在同圆或等圆中，如果两个圆周角相等，它们所对弧___________．
因为，在同圆或等圆中，如果圆周角相等，那么它所对的圆心角也相等，所以它所对的弧也相等．
·
C
B
O
A
F
G
E
（
（
相等
一定
在同圆（或等圆）中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半．
课堂小结
顶点在圆上，并且两边都和圆相交的角．
1． 圆周角
2． 圆周角定理
A
B
C
半圆（或直径）所对的圆周角是直角;
90°的圆周角所对的弦是直径．
3． 圆周角定理的推论
·
A
B
C1
O
C2
C3
┓
┓
┓
A
B
C
D
∴ ∠ ADC=∠BAD
∴AB∥CD．
随堂练习
1． 已知：AC = BD，
⌒
⌒
求证：AB∥CD．
证明：连接AD．
∵AC = BD，
⌒
⌒
2． 已知：⊙O中弦AB的等于半径，
求：弦AB所对的圆心角和圆周角的度数．
O
A
B
答：圆心角为60度．
圆周角为 30 度，
或 150 度．
C
D
3． AB是⊙O的直径，BD是⊙O的弦，延长BD到C，使AC=AB，BD与CD的大小有什么关系？为什么？
答：BD=CD
证明：连接AD
∵AB是⊙O的直径
∴∠ADB=90°
即AD⊥BC
又∵AC=AB
∴BD=CD
5． 在⊙O中，一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°，则x=_______．
4． 在直径为AB的半圆中，O为圆心，C、D为半圆上的两点，∠COD=50°，则∠CAD=______．
20°
25°
6． AB、AC为⊙O的两条弦，延长CA到D，使AD=AB，如果∠ADB=35°．
求∠BOC的度数．
∠BOC =140°
35°
70°
7． 点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？
A
B
C
D
1
2
3
4
5
6
7
8
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
由同弧来找相等的圆周角．
8． 你能设法确定一个圆形纸片的圆心吗？你有多少种方法？
D
A
B
C
O
O
O
·
方法一
方法二
方法三
方法四
A
B
9． 已知：∠A是圆O的圆周角，∠A=40°．
求：∠OBC的度数．
10． 已知：AB是⊙O的直径AB=10cm，
AC=6cm，∠ACB的平分线交⊙O于点D ．
求： BC， AD ，BD 的长．
10
6
11． AB是⊙O的直径， C 、D是圆上的两点，若∠ABD=40°，求∠BCD．
A
B
O
C
D
40°
12． 在⊙O中，∠CBD=30° ，∠BDC=20°，求∠A.
13． 在⊙O中，∠CBD=30° ，∠BDC=20°，求∠A.
1. ∠AOB = 60°，O到AB的距离是 mm.
2. 由已知可知∠B=75°，所以∠A =180°－∠B－∠C=30°.
3. AB = CD.
⌒
⌒
4. ∠ADC= ∠AOB=25°
习题答案