2021—2022学年八年级数学人教版上册11.2.2三角形的外角教学课件(20张ppt)
文档属性
| 名称 | 2021—2022学年八年级数学人教版上册11.2.2三角形的外角教学课件(20张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 00:00:00 | ||
图片预览







文档简介
A
C
D
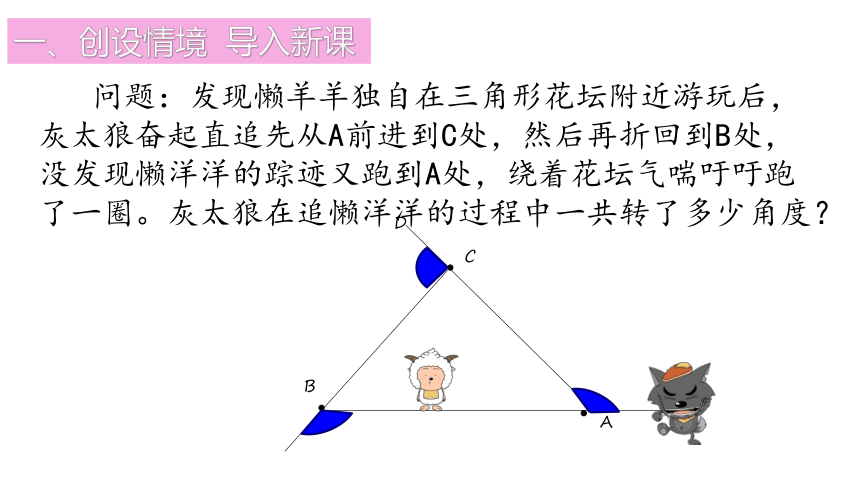
问题:发现懒羊羊独自在三角形花坛附近游玩后,灰太狼奋起直追先从A前进到C处,然后再折回到B处,没发现懒洋洋的踪迹又跑到A处,绕着花坛气喘吁吁跑了一圈。灰太狼在追懒洋洋的过程中一共转了多少角度?
一、创设情境 导入新课
B
11.2.三角形的外角(2)
二、展示交流、 感知概念
预习数学课本55页、思考以下问题:
1、什么叫三角形的外角?
2、三角形的外角有什么特征?
3、每个三角形的多少个外角?
4、每个顶点处,相对应的外角有怎样的数量关系?
5、每个外角与三角形的内角有怎样的位置关系?
及时检测
∠BEC是哪个三角形的外角?
∠BDC是哪个三角形的外角?
∠EFD是哪个三角形的外角?
△BCF
△ABC
△DCF
△BEF
△ABD
△AEC
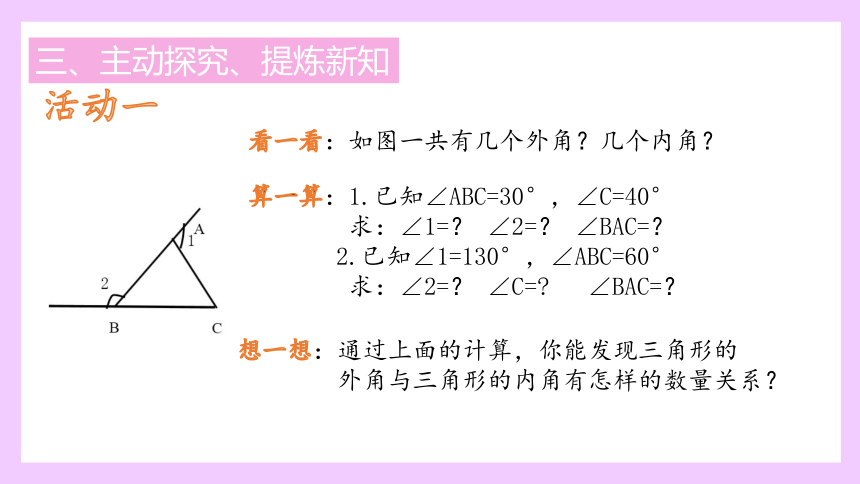
活动一
看一看:如图一共有几个外角?几个内角?
算一算:1.已知∠ABC=30°,∠C=40°
求:∠1=? ∠2=? ∠BAC=?
2.已知∠1=130°,∠ABC=60°
求:∠2=? ∠C=? ∠BAC=?
想一想:通过上面的计算,你能发现三角形的
外角与三角形的内角有怎样的数量关系?
三、主动探究、提炼新知
活动一
看一看:如图一共有几个外角?几个内角?
算一算:1.已知∠ABC=30°,∠C=40°
求:∠1=70° ∠2=150° ∠BAC=110°
2.已知∠1=130°,∠ABC=60°
求:∠2=120° ∠C= 70° ∠BAC=50°
想一想:通过上面的计算,你能发现三角形的
外角与三角形的内角有怎样的数量关系?
三、主动探究、提炼新知
探究:三角形的一个外角等于和它不相邻的两个外的和
证一证:
如图:已知∠1是△ABC的一个外角,求证:∠1=∠B+∠C
证明:在△ABC中
∠B+∠C+∠BAC=180°
∴∠B+∠C=180°-∠BAC
∵∠1+∠BAC=180°
∴∠1=180°-∠BAC
∴∠1=∠B+∠C
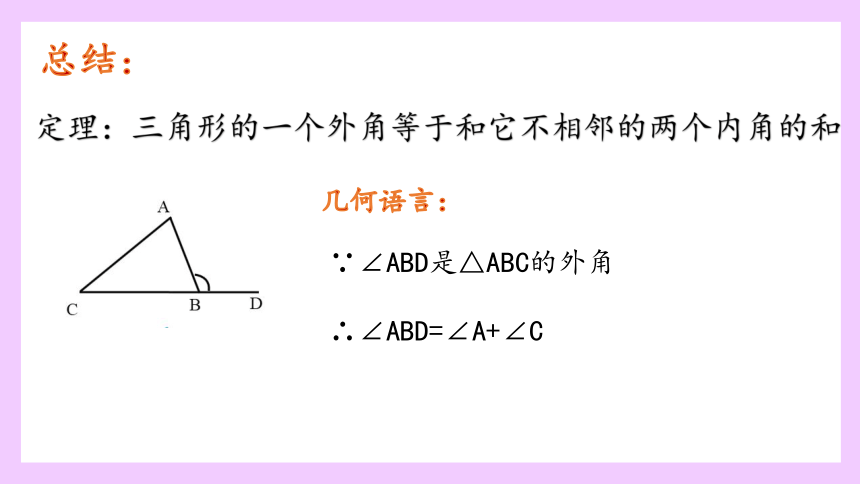
总结:
定理:三角形的一个外角等于和它不相邻的两个内角的和
几何语言:
∵∠ABD是△ABC的外角
∴∠ABD=∠A+∠C
牛刀小试
如图,已知∠A=40°,∠C=60°,求∠ABD?
解:∵∠ABD是△ABC的外角
∴∠ABD=∠A+∠C
∵∠A=40° ∠C=60°
∴∠ABD=40°+ 60°=100°
活动二
定理:三角形的一个外角大于任何一个和它不相邻的内角
∵∠ABD是△ABC的外角
∴∠ABD>∠A ∠ABD>∠C
几何语言:
四、经典示范,自然成长
已知:如图在△ABC中,∠B=∠C,AD平分外角∠EAC
求证:AD∥BC
证明:∵∠EAC=∠B+∠C
∠B=∠C
∴∠C=?∠EAC
∵AD平分∠EAC
∴∠DAC=?∠EAC
∴∠DAC=∠C
∴AD∥BC
五、智慧运用,养成能力
已知:如图在△ABC中,∠1是它的一个外角,E为边AC上的一点,延长BC到点D,连接DE。
求证:∠1>∠2
证明:∵∠1是△ABC的一个外角
∴∠1>∠3
∵∠3是△CDE的一个外角
∴∠3>∠2
∴∠1>∠2
六、问题解决,学会概括
前情回顾:发现懒羊羊独自在三角形花坛附近游玩后,灰太狼奋起直追先从A前进到C处,然后再折回到B处,没发现懒洋洋的踪迹又跑到A处,绕着花坛气喘吁吁跑了一圈。灰太狼在追懒洋洋的过程中一共转了多少角度?
解 :∵∠1是△ABC的一个外角
∴∠1=∠BCA+∠CBA
同理∠2=∠CBA+∠BAC
∠3=∠CAB+∠BCA
∴∠1+∠2+∠3=2 (∠BCA+∠CBA+∠CAB)
∵∠BCA+∠CBA+∠CAB=180°
∴∠1+∠2+∠3=2×180°=360°
A
C
D
B
七、畅所欲言,收获感悟
三角形的外角
定义
三角形的一边与另一边的反向延长线组成的角,叫做三角形的外角.
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角大于与它不相邻的任意一个内角.
三角形的外角和等于360°
八、课堂检测,精准评价
1、在ABC中,∠B=35°,∠C的外角等于110°,则∠A的度数是( )
A.35° B.65°
C.70° D.75°
D
解析:∵∠B=35°,∠C的外角等于110°,
∴∠A=110°-35°=75°.
2、如图,直线AB∥CD,∠A=70°,∠E=30°,则∠C等于( )
A.30°
B.40°
C.60°?
D.70°
解析:AE与CD交于F点,
∵AB∥CD,∠A=70°,
∴∠EFD=70°,
∵∠E=30°,
∴∠C=∠EFD-∠E=40°
B
3、如图,AB和CD相交于点O,则下列结论正确的是( )
A
A.∠1=∠2 B.∠2=∠3
C.∠1>∠4+∠5 D.∠2<∠5
解析:A.∵∠1和∠2是对顶角,∴∠1=∠2,故A正确;
B.∵∠2=∠A+∠3,∴∠2>∠3,故B错误;
C.∵∠1=∠4+∠5,故C错误;
D.∵∠2=∠4+∠5,∴∠2>∠5;故D错误;
B
4、如图,△ABC中,AB=AC,点D,E分别在边AC,BC上,且AD=AE,∠BAE=30°,则∠DEC=( )
A.12°B.15°C.18°D.30°
解析:设∠DEC=x,∠B=∠C=y,
∠ADE=∠DEC+∠C=x+y,
又∵AD=AE,
∴∠ADE=∠AED=x+y,
则∠AEC=∠AED+∠DEC=2x+y,
又∵∠AEC=∠B+∠BAE,
∴2x+y=y+30,
解得x=15,
∴∠DEC的度数是15°
5、如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )
c
A.15° B.20°C.25° D.30°
解析:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,
∴∠1=∠ACE,∠2=∠ABC,
又∵∠D=∠1-∠2,∠A=∠ACE-∠ABC,
∴∠D=∠A=25°.
课堂小结
教师寄语
数学的魅力就在于方法的多样性,同学们愿你们今后在数学的海洋里自由的畅游。
C
D
问题:发现懒羊羊独自在三角形花坛附近游玩后,灰太狼奋起直追先从A前进到C处,然后再折回到B处,没发现懒洋洋的踪迹又跑到A处,绕着花坛气喘吁吁跑了一圈。灰太狼在追懒洋洋的过程中一共转了多少角度?
一、创设情境 导入新课
B
11.2.三角形的外角(2)
二、展示交流、 感知概念
预习数学课本55页、思考以下问题:
1、什么叫三角形的外角?
2、三角形的外角有什么特征?
3、每个三角形的多少个外角?
4、每个顶点处,相对应的外角有怎样的数量关系?
5、每个外角与三角形的内角有怎样的位置关系?
及时检测
∠BEC是哪个三角形的外角?
∠BDC是哪个三角形的外角?
∠EFD是哪个三角形的外角?
△BCF
△ABC
△DCF
△BEF
△ABD
△AEC
活动一
看一看:如图一共有几个外角?几个内角?
算一算:1.已知∠ABC=30°,∠C=40°
求:∠1=? ∠2=? ∠BAC=?
2.已知∠1=130°,∠ABC=60°
求:∠2=? ∠C=? ∠BAC=?
想一想:通过上面的计算,你能发现三角形的
外角与三角形的内角有怎样的数量关系?
三、主动探究、提炼新知
活动一
看一看:如图一共有几个外角?几个内角?
算一算:1.已知∠ABC=30°,∠C=40°
求:∠1=70° ∠2=150° ∠BAC=110°
2.已知∠1=130°,∠ABC=60°
求:∠2=120° ∠C= 70° ∠BAC=50°
想一想:通过上面的计算,你能发现三角形的
外角与三角形的内角有怎样的数量关系?
三、主动探究、提炼新知
探究:三角形的一个外角等于和它不相邻的两个外的和
证一证:
如图:已知∠1是△ABC的一个外角,求证:∠1=∠B+∠C
证明:在△ABC中
∠B+∠C+∠BAC=180°
∴∠B+∠C=180°-∠BAC
∵∠1+∠BAC=180°
∴∠1=180°-∠BAC
∴∠1=∠B+∠C
总结:
定理:三角形的一个外角等于和它不相邻的两个内角的和
几何语言:
∵∠ABD是△ABC的外角
∴∠ABD=∠A+∠C
牛刀小试
如图,已知∠A=40°,∠C=60°,求∠ABD?
解:∵∠ABD是△ABC的外角
∴∠ABD=∠A+∠C
∵∠A=40° ∠C=60°
∴∠ABD=40°+ 60°=100°
活动二
定理:三角形的一个外角大于任何一个和它不相邻的内角
∵∠ABD是△ABC的外角
∴∠ABD>∠A ∠ABD>∠C
几何语言:
四、经典示范,自然成长
已知:如图在△ABC中,∠B=∠C,AD平分外角∠EAC
求证:AD∥BC
证明:∵∠EAC=∠B+∠C
∠B=∠C
∴∠C=?∠EAC
∵AD平分∠EAC
∴∠DAC=?∠EAC
∴∠DAC=∠C
∴AD∥BC
五、智慧运用,养成能力
已知:如图在△ABC中,∠1是它的一个外角,E为边AC上的一点,延长BC到点D,连接DE。
求证:∠1>∠2
证明:∵∠1是△ABC的一个外角
∴∠1>∠3
∵∠3是△CDE的一个外角
∴∠3>∠2
∴∠1>∠2
六、问题解决,学会概括
前情回顾:发现懒羊羊独自在三角形花坛附近游玩后,灰太狼奋起直追先从A前进到C处,然后再折回到B处,没发现懒洋洋的踪迹又跑到A处,绕着花坛气喘吁吁跑了一圈。灰太狼在追懒洋洋的过程中一共转了多少角度?
解 :∵∠1是△ABC的一个外角
∴∠1=∠BCA+∠CBA
同理∠2=∠CBA+∠BAC
∠3=∠CAB+∠BCA
∴∠1+∠2+∠3=2 (∠BCA+∠CBA+∠CAB)
∵∠BCA+∠CBA+∠CAB=180°
∴∠1+∠2+∠3=2×180°=360°
A
C
D
B
七、畅所欲言,收获感悟
三角形的外角
定义
三角形的一边与另一边的反向延长线组成的角,叫做三角形的外角.
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角大于与它不相邻的任意一个内角.
三角形的外角和等于360°
八、课堂检测,精准评价
1、在ABC中,∠B=35°,∠C的外角等于110°,则∠A的度数是( )
A.35° B.65°
C.70° D.75°
D
解析:∵∠B=35°,∠C的外角等于110°,
∴∠A=110°-35°=75°.
2、如图,直线AB∥CD,∠A=70°,∠E=30°,则∠C等于( )
A.30°
B.40°
C.60°?
D.70°
解析:AE与CD交于F点,
∵AB∥CD,∠A=70°,
∴∠EFD=70°,
∵∠E=30°,
∴∠C=∠EFD-∠E=40°
B
3、如图,AB和CD相交于点O,则下列结论正确的是( )
A
A.∠1=∠2 B.∠2=∠3
C.∠1>∠4+∠5 D.∠2<∠5
解析:A.∵∠1和∠2是对顶角,∴∠1=∠2,故A正确;
B.∵∠2=∠A+∠3,∴∠2>∠3,故B错误;
C.∵∠1=∠4+∠5,故C错误;
D.∵∠2=∠4+∠5,∴∠2>∠5;故D错误;
B
4、如图,△ABC中,AB=AC,点D,E分别在边AC,BC上,且AD=AE,∠BAE=30°,则∠DEC=( )
A.12°B.15°C.18°D.30°
解析:设∠DEC=x,∠B=∠C=y,
∠ADE=∠DEC+∠C=x+y,
又∵AD=AE,
∴∠ADE=∠AED=x+y,
则∠AEC=∠AED+∠DEC=2x+y,
又∵∠AEC=∠B+∠BAE,
∴2x+y=y+30,
解得x=15,
∴∠DEC的度数是15°
5、如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=( )
c
A.15° B.20°C.25° D.30°
解析:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,
∴∠1=∠ACE,∠2=∠ABC,
又∵∠D=∠1-∠2,∠A=∠ACE-∠ABC,
∴∠D=∠A=25°.
课堂小结
教师寄语
数学的魅力就在于方法的多样性,同学们愿你们今后在数学的海洋里自由的畅游。
