2021-2022学年人教版九年级数学上册24.3 正多边形和圆(2)教学课件(24张PPT)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.3 正多边形和圆(2)教学课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 08:34:43 | ||
图片预览




文档简介
正多边形和圆(2)
神秘的
割圆术
刘徽
学习目标
1. 从正多边形的对称性出发,理解正多边形的
中心、半径、边心距、中心角的概念;
2. 通过探究发现正多边形与圆的关系;
3. 了解正多边形的半径、边长和边心距之间的关系;
4. 能把正多边形的计算问题转化为解直角三角形问题.
探究一
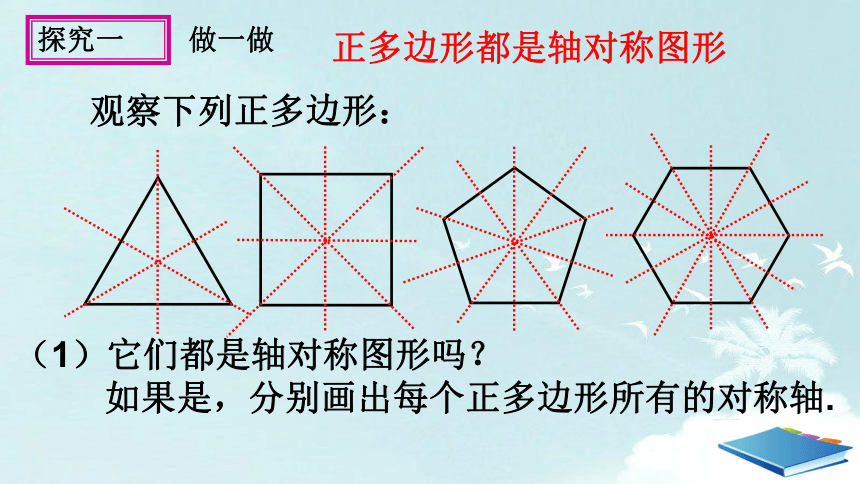
观察下列正多边形:
(1)它们都是轴对称图形吗?
如果是,分别画出每个正多边形所有的对称轴.
做一做
正多边形都是轴对称图形
探究一
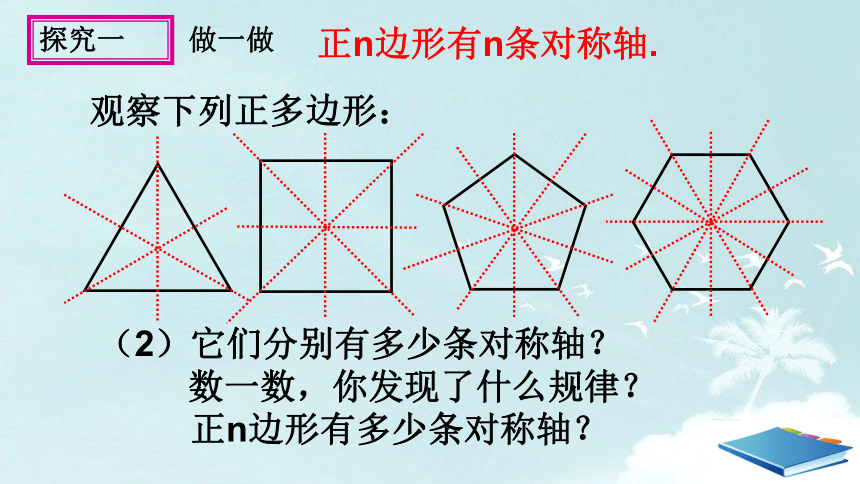
观察下列正多边形:
(2)它们分别有多少条对称轴?
数一数,你发现了什么规律?
正n边形有多少条对称轴?
做一做
正n边形有n条对称轴.
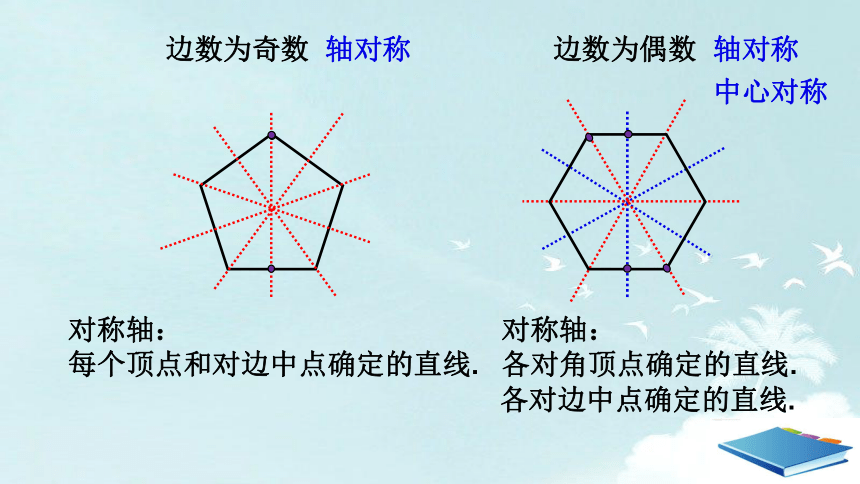
对称轴:
每个顶点和对边中点确定的直线.
边数为奇数
边数为偶数
对称轴:
各对角顶点确定的直线.
各对边中点确定的直线.
轴对称
轴对称
中心对称
探究一
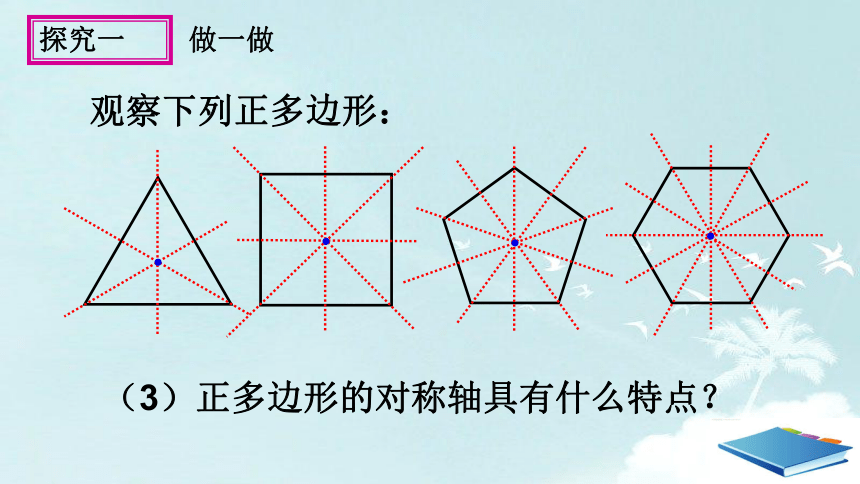
观察下列正多边形:
(3)正多边形的对称轴具有什么特点?
做一做
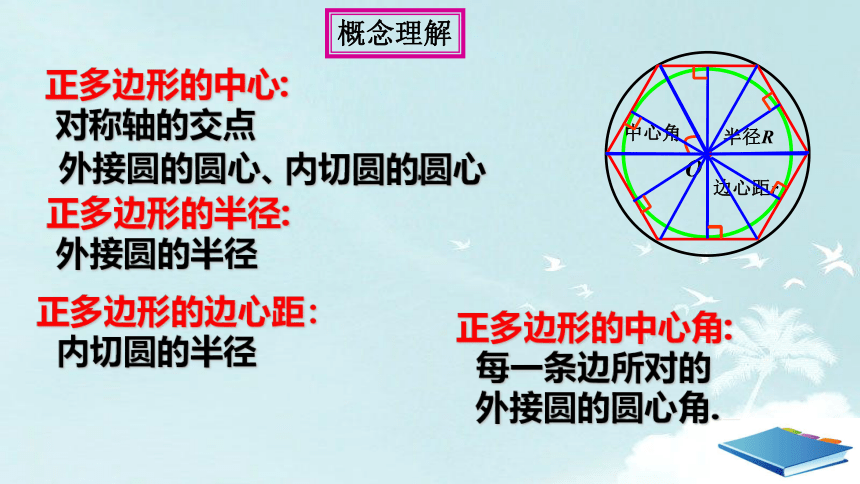
概念理解
·
半径R
边心距r
O
中心角
正多边形的中心:
对称轴的交点
正多边形的半径:
外接圆的半径
正多边形的中心角:
每一条边所对的
外接圆的圆心角.
正多边形的边心距:
内切圆的半径
外接圆的圆心、 .
内切圆的圆心
1、O是正△ABC的中心,它是△ABC的 圆与 圆的圆心。
外接
内切
半径
外接
边心距
内切
巩固新知
OB叫正△ABC的 ,它是正△ABC的 圆的半径。
OD叫作正△ABC的 ,
它是正△ABC的 圆的半径。
中心
边心距
2、正方形ABCD的外接圆圆心O叫做正方形ABCD的
正方形ABCD的内切圆的半径OE叫做正方形ABCD的
巩固新知
边心距
中心角
3、⊙O是正五边形ABCDE的外接圆,
O点到弦AB的距离OF叫正五边形ABCDE的
∠AOB叫做正五边形ABCDE的 ,
巩固新知
∠AOB
4、图中正六边形ABCDEF的中心角是
巩固新知
(1)正三角形中心角是多少度?你是怎样得到的?
探究二
议一议
正方形的呢?
正n边形的中心角呢?
正五边形的呢?
(2)将正n边形以它的中心为旋转中心,
以它的中心角的度数为旋转角进行旋转,你有什么发现?
探究二
A1
A2
A3
A4
A5
A6
A7
An
O
旋转对称性
议一议
探究二
以等腰三角形作为“基本图形”连续旋转(n-1)次,
得到正 n 边形.
议一议
(3)过正n边形顶点的n条半径把正n边形分成_____个全等
的等腰三角形,每个等腰三角形又被边心距分成两个全等的
_______三角形.
·
A1
A2
A3
A4
A5
A6
A7
An
O
n
直角
A2
A7
An
A6
A5
A4
A3
A1
O
探究二
议一议
学校花园中央有一个亭子,它的地基是边长为6m的正六边形,你知道它的面积是多少吗?
学以致用
割圆术
回顾本节课,我想说…
思考 ? 收获
我学会了…
我知道了…
我懂得了…
·
A
B
C
D
O
E
当堂检测
1.正三角形ABC的外接圆圆心O叫做正三角形ABC的___________.
2.正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
3.正五边形的半径是正五边形ABCDE的__________圆的半径.
4. 正六边形ABCDEF的中心角是_______度.
5.如右图,半径为 6cm 的圆内正方形的边长为______,
边心距为_______,面积为_______.
各边相等的圆内接四边形是正方形吗?各角相等的圆内接四边形呢?如果是,说明理由;如果不是,举出反例.
深度思考
作 业
必做: 《伴你学》38页1-----9.
选做:《伴你学》39页10-----11.
神秘的
割圆术
刘徽
学习目标
1. 从正多边形的对称性出发,理解正多边形的
中心、半径、边心距、中心角的概念;
2. 通过探究发现正多边形与圆的关系;
3. 了解正多边形的半径、边长和边心距之间的关系;
4. 能把正多边形的计算问题转化为解直角三角形问题.
探究一
观察下列正多边形:
(1)它们都是轴对称图形吗?
如果是,分别画出每个正多边形所有的对称轴.
做一做
正多边形都是轴对称图形
探究一
观察下列正多边形:
(2)它们分别有多少条对称轴?
数一数,你发现了什么规律?
正n边形有多少条对称轴?
做一做
正n边形有n条对称轴.
对称轴:
每个顶点和对边中点确定的直线.
边数为奇数
边数为偶数
对称轴:
各对角顶点确定的直线.
各对边中点确定的直线.
轴对称
轴对称
中心对称
探究一
观察下列正多边形:
(3)正多边形的对称轴具有什么特点?
做一做
概念理解
·
半径R
边心距r
O
中心角
正多边形的中心:
对称轴的交点
正多边形的半径:
外接圆的半径
正多边形的中心角:
每一条边所对的
外接圆的圆心角.
正多边形的边心距:
内切圆的半径
外接圆的圆心、 .
内切圆的圆心
1、O是正△ABC的中心,它是△ABC的 圆与 圆的圆心。
外接
内切
半径
外接
边心距
内切
巩固新知
OB叫正△ABC的 ,它是正△ABC的 圆的半径。
OD叫作正△ABC的 ,
它是正△ABC的 圆的半径。
中心
边心距
2、正方形ABCD的外接圆圆心O叫做正方形ABCD的
正方形ABCD的内切圆的半径OE叫做正方形ABCD的
巩固新知
边心距
中心角
3、⊙O是正五边形ABCDE的外接圆,
O点到弦AB的距离OF叫正五边形ABCDE的
∠AOB叫做正五边形ABCDE的 ,
巩固新知
∠AOB
4、图中正六边形ABCDEF的中心角是
巩固新知
(1)正三角形中心角是多少度?你是怎样得到的?
探究二
议一议
正方形的呢?
正n边形的中心角呢?
正五边形的呢?
(2)将正n边形以它的中心为旋转中心,
以它的中心角的度数为旋转角进行旋转,你有什么发现?
探究二
A1
A2
A3
A4
A5
A6
A7
An
O
旋转对称性
议一议
探究二
以等腰三角形作为“基本图形”连续旋转(n-1)次,
得到正 n 边形.
议一议
(3)过正n边形顶点的n条半径把正n边形分成_____个全等
的等腰三角形,每个等腰三角形又被边心距分成两个全等的
_______三角形.
·
A1
A2
A3
A4
A5
A6
A7
An
O
n
直角
A2
A7
An
A6
A5
A4
A3
A1
O
探究二
议一议
学校花园中央有一个亭子,它的地基是边长为6m的正六边形,你知道它的面积是多少吗?
学以致用
割圆术
回顾本节课,我想说…
思考 ? 收获
我学会了…
我知道了…
我懂得了…
·
A
B
C
D
O
E
当堂检测
1.正三角形ABC的外接圆圆心O叫做正三角形ABC的___________.
2.正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
3.正五边形的半径是正五边形ABCDE的__________圆的半径.
4. 正六边形ABCDEF的中心角是_______度.
5.如右图,半径为 6cm 的圆内正方形的边长为______,
边心距为_______,面积为_______.
各边相等的圆内接四边形是正方形吗?各角相等的圆内接四边形呢?如果是,说明理由;如果不是,举出反例.
深度思考
作 业
必做: 《伴你学》38页1-----9.
选做:《伴你学》39页10-----11.
同课章节目录
