2021-2022 学年人教版九年级数学上册课件23.2.1 中心对称(共23张PPT)
文档属性
| 名称 | 2021-2022 学年人教版九年级数学上册课件23.2.1 中心对称(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 08:35:33 | ||
图片预览



文档简介
23.2.1 中心对称
观察下面的每组图形,你觉得它们之间有怎样的位置关系?
轴对称
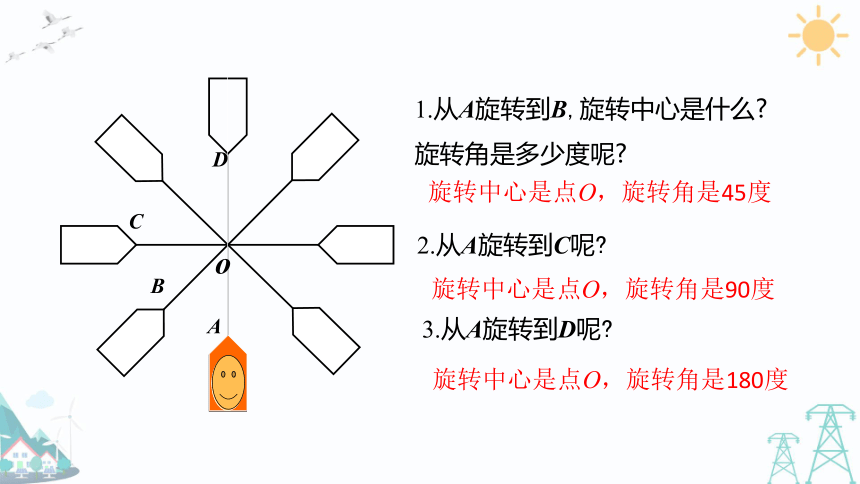
1.从A旋转到B,旋转中心是什么?旋转角是多少度呢?
o
A
B
C
D
2.从A旋转到C呢?
3.从A旋转到D呢?
旋转中心是点O,旋转角是45度
旋转中心是点O,旋转角是90度
旋转中心是点O,旋转角是180度
观察下面的每组两个图形,它们之间还是轴对称关系吗?
NO
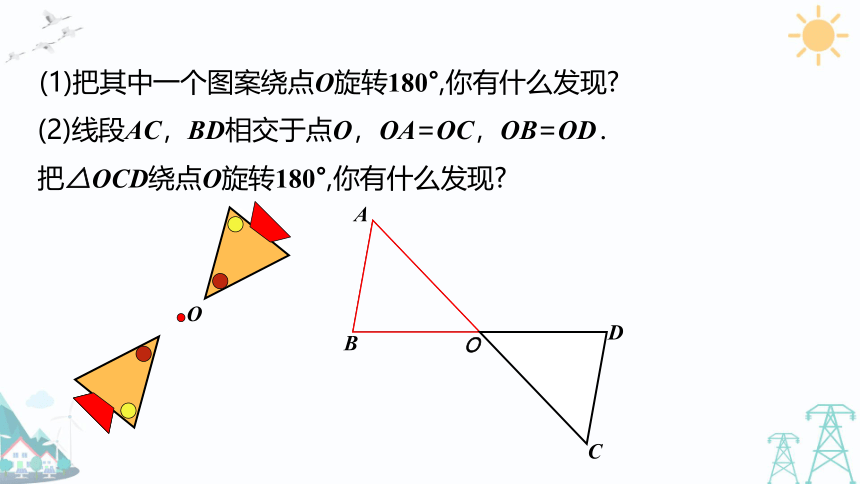
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.
把△OCD绕点O旋转180°,你有什么发现?
O
C
O
B
D
A
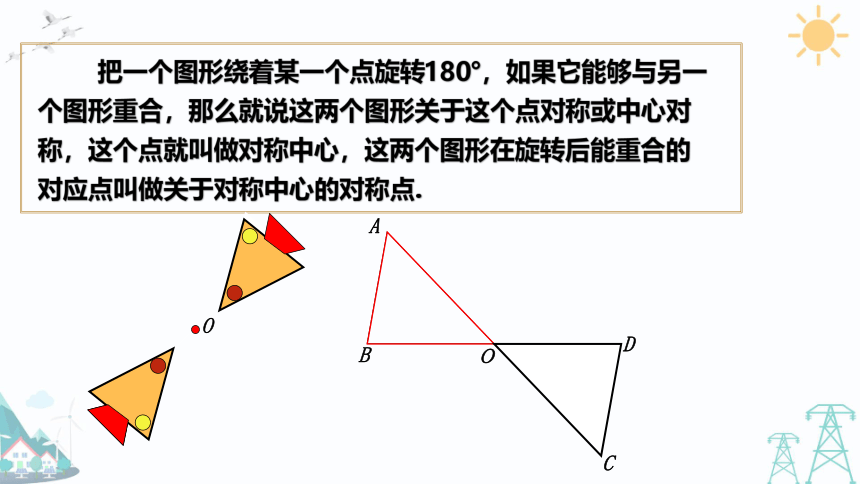
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做对称中心,这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
O
C
O
B
D
A
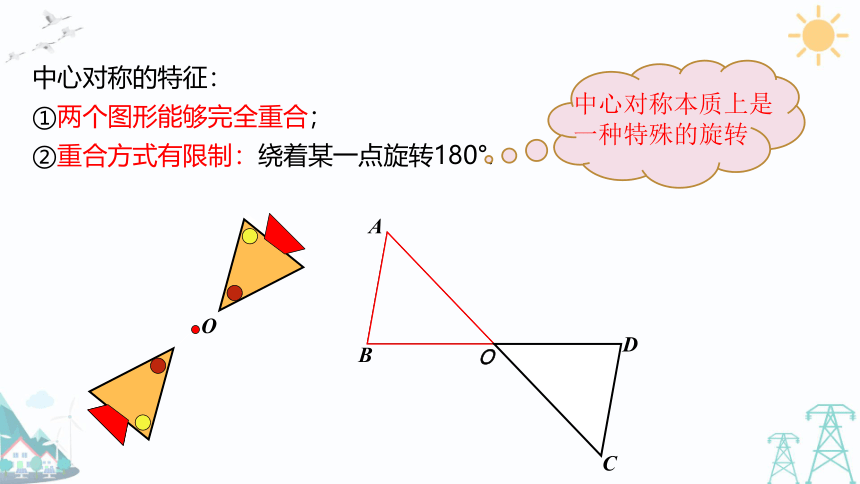
中心对称的特征:
①两个图形能够完全重合;
②重合方式有限制:绕着某一点旋转180°.
中心对称本质上是一种特殊的旋转
O
C
O
B
D
A
C
O
B
D
A
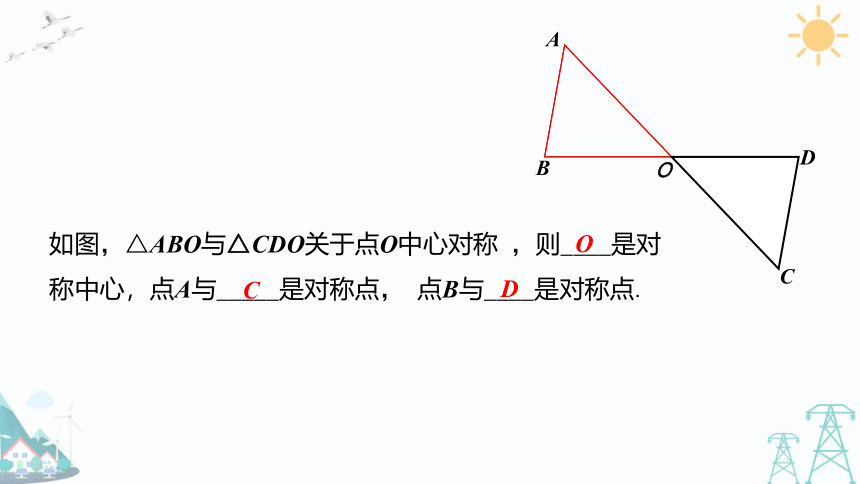
如图,△ABO与△CDO关于点O中心对称 ,则____是对
称中心,点A与_____是对称点, 点B与____是对称点.
O
C
D
例1 如图所示的图形中成中心对称的有____组.
3
如图,旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转
180°,画出△A′B′C′;
第三步,移开三角板.
这样画出的△ABC 与△A′B′C′关于点O对称,分别连接对称点AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
C
A
B
C
A
B
A′
B′
O
C′
C
A
B
A′
B′
O
C′
1. 中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等图形
中心对称的性质
对称中心的确定
方法1:对称中心为任意两个对应点连接的线段的中点
方法2:对称中心为任意两组对应点连接的线段的交点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
轴 对 称
中心对称
1
有一条对称轴—— 直线
有一个对称中心——点
2
图形沿轴对折(翻转180°)
图形绕中心旋转180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
4
对应点的连线被对称轴垂直平分
对称点所连线段经过对称中心并被平分
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
例2 (1)如图(1),选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图(2),选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
图(1)
图(2)
解:(1)如图(3),连接AO,在AO的延长线上截取OA′=OA,
即可以求得点A关于点O的对称点A′.
(2)如图(4),作出A,B,C三点关于点O的对称点A′,B′,C′,依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于点O对称的△A′B′C′.
图(3)
图(4)
作中心对称的图形的一般步骤是:
①确定代表性的点(线段的端点);
②作出每个代表性的点的对称点;
③按照原图形的形状顺次连接各对称点.
1.判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.( )
(2)成中心对称的两个图形一定是全等形.但全等的两个图形不一定是成中心对称的图形. ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形. ( )
√
√
×
2.如图所示的5组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
B
3.如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
D
4. 如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 则对称中心E点的坐标是__________.
(3,-1)
5.如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
A
B
C
D
O
作法:
1.连接AO并延长到A',使OA'=OA,得到点A的对应点A';
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
A
B
C
D
O
A'
B'
C'
D'
概念
旋转角是180°
性质
1.对应点的连线经过对称中心,且被对称中心平分;
2.中心对称两个图形是全等的
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
观察下面的每组图形,你觉得它们之间有怎样的位置关系?
轴对称
1.从A旋转到B,旋转中心是什么?旋转角是多少度呢?
o
A
B
C
D
2.从A旋转到C呢?
3.从A旋转到D呢?
旋转中心是点O,旋转角是45度
旋转中心是点O,旋转角是90度
旋转中心是点O,旋转角是180度
观察下面的每组两个图形,它们之间还是轴对称关系吗?
NO
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.
把△OCD绕点O旋转180°,你有什么发现?
O
C
O
B
D
A
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做对称中心,这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
O
C
O
B
D
A
中心对称的特征:
①两个图形能够完全重合;
②重合方式有限制:绕着某一点旋转180°.
中心对称本质上是一种特殊的旋转
O
C
O
B
D
A
C
O
B
D
A
如图,△ABO与△CDO关于点O中心对称 ,则____是对
称中心,点A与_____是对称点, 点B与____是对称点.
O
C
D
例1 如图所示的图形中成中心对称的有____组.
3
如图,旋转三角板,画关于点O对称的两个三角形:
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转
180°,画出△A′B′C′;
第三步,移开三角板.
这样画出的△ABC 与△A′B′C′关于点O对称,分别连接对称点AA′,BB′,CC′.点O在线段AA′上吗?如果在,在什么位置? △ABC与△A′B′C′有什么关系?
C
A
B
C
A
B
A′
B′
O
C′
C
A
B
A′
B′
O
C′
1. 中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线)
2.中心对称的两个图形是全等图形
中心对称的性质
对称中心的确定
方法1:对称中心为任意两个对应点连接的线段的中点
方法2:对称中心为任意两组对应点连接的线段的交点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
轴 对 称
中心对称
1
有一条对称轴—— 直线
有一个对称中心——点
2
图形沿轴对折(翻转180°)
图形绕中心旋转180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
4
对应点的连线被对称轴垂直平分
对称点所连线段经过对称中心并被平分
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
例2 (1)如图(1),选择点O为对称中心,画出点A关于点O的对称点A′;
(2)如图(2),选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
图(1)
图(2)
解:(1)如图(3),连接AO,在AO的延长线上截取OA′=OA,
即可以求得点A关于点O的对称点A′.
(2)如图(4),作出A,B,C三点关于点O的对称点A′,B′,C′,依次连接A′B′,B′C′,C′A′,就可得到与△ABC关于点O对称的△A′B′C′.
图(3)
图(4)
作中心对称的图形的一般步骤是:
①确定代表性的点(线段的端点);
②作出每个代表性的点的对称点;
③按照原图形的形状顺次连接各对称点.
1.判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形不一定是轴对称的图形.( )
(2)成中心对称的两个图形一定是全等形.但全等的两个图形不一定是成中心对称的图形. ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴对称的图形. ( )
√
√
×
2.如图所示的5组图形中,左边的图形与右边的图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
B
3.如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
D
4. 如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 则对称中心E点的坐标是__________.
(3,-1)
5.如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
A
B
C
D
O
作法:
1.连接AO并延长到A',使OA'=OA,得到点A的对应点A';
2.同理,可作出点B,C,D的对应点B',C',D';
3.顺次连接A',B',C',D',则四边形A'B'C'D'即为所作.
A
B
C
D
O
A'
B'
C'
D'
概念
旋转角是180°
性质
1.对应点的连线经过对称中心,且被对称中心平分;
2.中心对称两个图形是全等的
作图
应用1:作中心对称图形;
应用2:找出对称中心.
中心对称
同课章节目录
