2021-2022学年苏科版数学九年级上册2.5直线与圆的位置关系 课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级上册2.5直线与圆的位置关系 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 08:58:08 | ||
图片预览








文档简介
(共27张PPT)
第二章
对称图形—圆
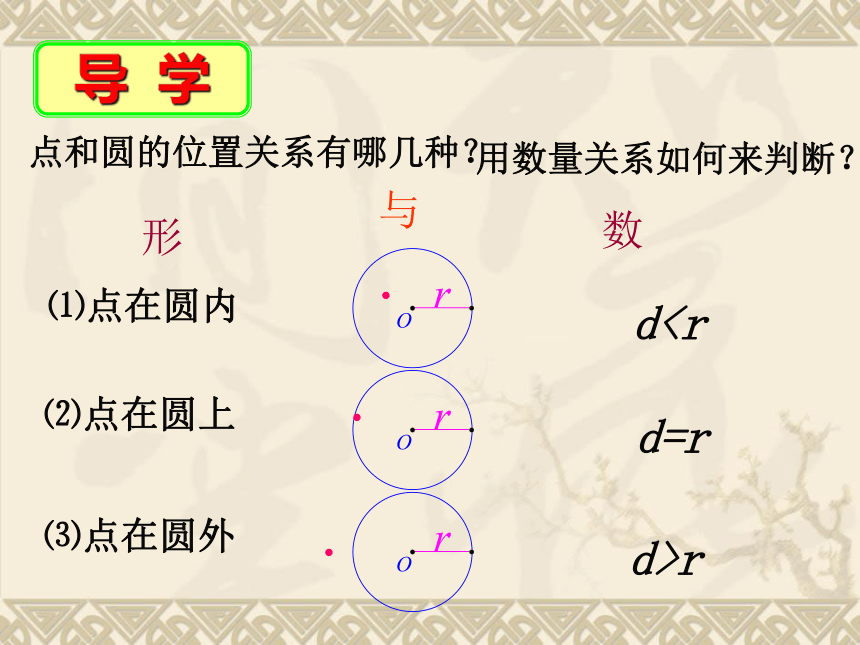
点和圆的位置关系有哪几种?
⑴点在圆内
⑵点在圆上
⑶点在圆外
dd=r
d>r
·
·
·
用数量关系如何来判断?
导
学
形
数
与
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
教学目标
(1)了解直线和圆的位置关系和有关概念。
(2)理解和掌握直线和圆的位置关系判别方法。
(3)通过实物和课件演示让学生体验数形结合的数学思想。从而提高学生的画图、识图能力。
(4)由点和圆的位置关系归纳、类比出直线和圆的位置关系,从而提高学生的知识迁移能力。
重点
直线和圆的三种位置关系和两种判别方法。
难点
由上节课点和圆的位置关系迁移并导出
直线和圆的位置关系的三个对应等价。
(2)如图,在练习本上画一条直线
l,把钥匙环看作一个圆,在本上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线l的公共点的个数的变化情况吗?
探究新知
合作完成
通过刚才的动手操作与观察,你发现直线和圆的公共点个数有几种情况?(请把你的发现在纸上画出来)
①直线和圆
公共点,这时我们说直线和圆
,这条直线叫做圆的
这个点叫
如图1
③直线和圆
公共点,这时我们说直线和圆
.如图3
②直线和圆
公共点,这时我们说直线和圆
,这条直线叫做圆的
,这个点叫做
如图2
如图1
如图2
如图3
有两个
相交
割线
只有一个
相切
切线
切点
没有
相离
交点
知识整理
直线与圆的位置关系
直线与圆的
位置关系
相交
相切
相离
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2
个
交点
割线
1
个
切点
切线
没有
d
r
O
l
l
r
d
O
d
r
O
l
1、直线与圆最多有两个公共
点
。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。…
…
…
…(
)
3
、若A、B是⊙O外两点,
则直线AB
与⊙O相离。…
…
…
…
…(
)
√
×
谁是谁非
.A
.B
.C
.O
.O
m
×
.A
.B
.O
1、看图判断直线l与
⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
(5)
?
l
如果,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”也能像“点和圆的位置关系”一样进行数量分析吗?
1、连结直线外一点与直线上所
有点的线段中,最短的是______?
2.直线外一点到这条直线
垂线段的长度叫点到直线
的距离。
垂线段
a
.A
D
O
a
P
d
r
P
d
P
a
思考:当直线与圆
相离、相切、
相交时,d与
r有何关系?
1、直线与圆相离
=>
d>r
2、直线与圆相切
=>
d=r
3、直线与圆相交
=>
d我们把圆心到直线
的距离用d表示,
半径用r表示
<
<
<
知识整理
直线与圆的位置关系
直线与圆的
位置关系
相交
相切
相离
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
d
<
r
d
=
r
d
>
r
2
个
交点
割线
1
个
切点
切线
没有
d
r
O
l
l
r
d
O
d
r
O
l
判定直线与圆的位置关系的方法有____种:
(1)由________________
的个数来判断;
(2)由____________________________的数量大小关系来判断.
两
直线与圆的公共点
圆心到直线的距离d与半径r
说一说
例
在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,
设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。
(1)
r
=
2厘米
(2)r
=2.4厘米
(3)r
=3厘米
4cm
3cm
B
C
A
讨论
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当r满足________________时,⊙C与直线AB相离。
2、当r满足____________
时,⊙C与直线AB相切。
3、当r满足____________时,
⊙C与直线AB相交。
B
C
A
D
4
5
d=2.4cm
3
0cmr=2.4cm
r>2.4cm
在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
当r满足___________
_____________
时,⊙C与线段AB只有一个公共点.
r=2.4cm
B
C
A
D
4
5
3
d=2.4cm
或3cm1.⊙O的半径为3
,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d
>3
B.d<3
C.d
≤3
D.d
=3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( ):
A.相离
B.相交
C.相切
D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.(
)
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.7的圆与直线BC的位置关系是
,以A为圆心,
为半径的圆与直线BC相切.
A
C
√
相离
完成练习
5、已知⊙O的半径为3,点A在直线l上,点A到⊙O的圆心O的距离为3,则l与⊙O的位置关系为
。
·
·
O
O
A
A
l
l
A.相离
B.相切
C.相交
D.相交或相切
D
如图,P为正比例函数
图象上一个动点,⊙P的半径为3,设点P的坐标为(x,y).
(1)求⊙P与直线x=2相切时点P的坐标;
(2)请直接写出⊙P与直线x=2相交、相离时x的取值范围;
已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,设AD为x.
(1)如图1,当x为何值时,⊙O与AM相切;
(2)如图2,当x为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
2、识别直线与圆的位置关系的方法:
(1)一种是根据直线和圆的公共点个数进行识别:
直线L与⊙o没有公共点
直线L与⊙o相离。
直线L与⊙o只有一个公共点
直线L与⊙o相切。
直线L与⊙o有两个公共点
直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r
直线L与⊙o相离;
d=r
直线L与⊙o相切;
d直线L与⊙o相交。
1、直线与圆的位置关系3种:相离、相切和相交。
布置作业:
1、
教材P102练习1、2
2、如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?
⑴ r
=2cm;
⑵
r
=4cm;⑶
r
=2.5cm。
O
A
B
M
C
.
第二章
对称图形—圆
点和圆的位置关系有哪几种?
⑴点在圆内
⑵点在圆上
⑶点在圆外
d
d>r
·
·
·
用数量关系如何来判断?
导
学
形
数
与
(1)如图,思考在太阳升起的过程中,太阳和地平线会有几种位置关系?我们把太阳看作一个圆,地平线看作一条直线,由此你能得出直线和圆的位置关系吗?
教学目标
(1)了解直线和圆的位置关系和有关概念。
(2)理解和掌握直线和圆的位置关系判别方法。
(3)通过实物和课件演示让学生体验数形结合的数学思想。从而提高学生的画图、识图能力。
(4)由点和圆的位置关系归纳、类比出直线和圆的位置关系,从而提高学生的知识迁移能力。
重点
直线和圆的三种位置关系和两种判别方法。
难点
由上节课点和圆的位置关系迁移并导出
直线和圆的位置关系的三个对应等价。
(2)如图,在练习本上画一条直线
l,把钥匙环看作一个圆,在本上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线l的公共点的个数的变化情况吗?
探究新知
合作完成
通过刚才的动手操作与观察,你发现直线和圆的公共点个数有几种情况?(请把你的发现在纸上画出来)
①直线和圆
公共点,这时我们说直线和圆
,这条直线叫做圆的
这个点叫
如图1
③直线和圆
公共点,这时我们说直线和圆
.如图3
②直线和圆
公共点,这时我们说直线和圆
,这条直线叫做圆的
,这个点叫做
如图2
如图1
如图2
如图3
有两个
相交
割线
只有一个
相切
切线
切点
没有
相离
交点
知识整理
直线与圆的位置关系
直线与圆的
位置关系
相交
相切
相离
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2
个
交点
割线
1
个
切点
切线
没有
d
r
O
l
l
r
d
O
d
r
O
l
1、直线与圆最多有两个公共
点
。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。…
…
…
…(
)
3
、若A、B是⊙O外两点,
则直线AB
与⊙O相离。…
…
…
…
…(
)
√
×
谁是谁非
.A
.B
.C
.O
.O
m
×
.A
.B
.O
1、看图判断直线l与
⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
(5)
?
l
如果,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”也能像“点和圆的位置关系”一样进行数量分析吗?
1、连结直线外一点与直线上所
有点的线段中,最短的是______?
2.直线外一点到这条直线
垂线段的长度叫点到直线
的距离。
垂线段
a
.A
D
O
a
P
d
r
P
d
P
a
思考:当直线与圆
相离、相切、
相交时,d与
r有何关系?
1、直线与圆相离
=>
d>r
2、直线与圆相切
=>
d=r
3、直线与圆相交
=>
d
的距离用d表示,
半径用r表示
<
<
<
知识整理
直线与圆的位置关系
直线与圆的
位置关系
相交
相切
相离
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
d
<
r
d
=
r
d
>
r
2
个
交点
割线
1
个
切点
切线
没有
d
r
O
l
l
r
d
O
d
r
O
l
判定直线与圆的位置关系的方法有____种:
(1)由________________
的个数来判断;
(2)由____________________________的数量大小关系来判断.
两
直线与圆的公共点
圆心到直线的距离d与半径r
说一说
例
在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,
设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。
(1)
r
=
2厘米
(2)r
=2.4厘米
(3)r
=3厘米
4cm
3cm
B
C
A
讨论
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当r满足________________时,⊙C与直线AB相离。
2、当r满足____________
时,⊙C与直线AB相切。
3、当r满足____________时,
⊙C与直线AB相交。
B
C
A
D
4
5
d=2.4cm
3
0cm
r>2.4cm
在Rt△ABC中,∠C=90°,
AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。
当r满足___________
_____________
时,⊙C与线段AB只有一个公共点.
r=2.4cm
B
C
A
D
4
5
3
d=2.4cm
或3cm
,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d
>3
B.d<3
C.d
≤3
D.d
=3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( ):
A.相离
B.相交
C.相切
D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.(
)
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.7的圆与直线BC的位置关系是
,以A为圆心,
为半径的圆与直线BC相切.
A
C
√
相离
完成练习
5、已知⊙O的半径为3,点A在直线l上,点A到⊙O的圆心O的距离为3,则l与⊙O的位置关系为
。
·
·
O
O
A
A
l
l
A.相离
B.相切
C.相交
D.相交或相切
D
如图,P为正比例函数
图象上一个动点,⊙P的半径为3,设点P的坐标为(x,y).
(1)求⊙P与直线x=2相切时点P的坐标;
(2)请直接写出⊙P与直线x=2相交、相离时x的取值范围;
已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,设AD为x.
(1)如图1,当x为何值时,⊙O与AM相切;
(2)如图2,当x为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
2、识别直线与圆的位置关系的方法:
(1)一种是根据直线和圆的公共点个数进行识别:
直线L与⊙o没有公共点
直线L与⊙o相离。
直线L与⊙o只有一个公共点
直线L与⊙o相切。
直线L与⊙o有两个公共点
直线L与⊙o相交。
(2)另一种是根据圆心到直线的距离d与圆半径r数量
比较来进行识别:
d>r
直线L与⊙o相离;
d=r
直线L与⊙o相切;
d
1、直线与圆的位置关系3种:相离、相切和相交。
布置作业:
1、
教材P102练习1、2
2、如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?
⑴ r
=2cm;
⑵
r
=4cm;⑶
r
=2.5cm。
O
A
B
M
C
.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
