平行四边形判定1
图片预览







文档简介
(共26张PPT)
过程分析
目的分析
教法分析
评价分析
教材分析
(一)教材的地位和作用
1、是平行线和全等三角形知识的应用和延伸;
2、对其他的特殊四边形的判定定理具有指导意义,为学习其他特殊四边形判定定理奠定基础;
3、便于学生弄清平行四边形和其他特殊平行四边形的特性、共性及他们之间的从属关系.
教材分析
过程分析
目的分析
教法分析
评价分析
重点:
平行四边形的判定定理及其 运用.
难点:判定定理的推导过程.
教材分析
过程分析
目的分析
教法分析
评价分析
教材分析
过程分析
目的分析
教法分析
评价分析
2、方法与过程:探索由三角形补成平行四边形的方法,由此发现平行四边形的判定.
3、情感态度价值观:经过自主探索和合作交流,敢于发表自己的观点,能从交流中获益.
1、知识与技能:掌握平行四边形判定定理,并会运用判定定理解决相关问题.
教材分析
过程分析
教法分析
目的分析
评价分析
情境教学法 课堂研讨法
1、培养学生的自学能力;
2、落实学生的主体地位,促进学生的主动发展;
3、为培养学生的创新意识与创新能力奠定基础.
教材分析
过程分析
教法分析
目的分析
评价分析
1、指导学生如何将实际问题转化为数学问题,明白数学与人类的密切关系;
2、指导学生通过类比、联想、推理等思维进行数学研究;
3、明白动手实践,自主探索、合作交流是我们学习的重要方式;明白现代信息技术的发展对我们数学有着重大的帮助.
教材分析
过程分析
目的分析
教法分析
评价分析
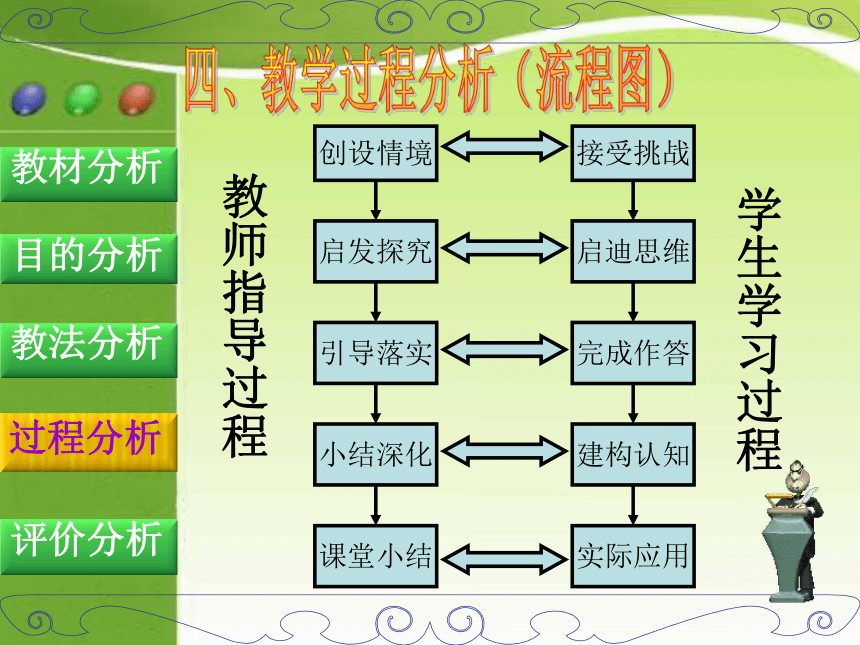
创设情境
启发探究
引导落实
小结深化
课堂小结
接受挑战
启迪思维
完成作答
实际应用
建构认知
教师指导过程
学生学习过程
教学过程分析
(1)复习平行四边形定义、性质
教学过程分析
(2)上演小话剧:一位男生不小心把老师的平行四边形玻璃教具打裂,剩下最大的一块保留了平行四边形的三个顶点,这名同学拿到玻璃店,却无法复制一块原模原样的,该生一筹莫展。提出问题“如何把三角形的玻璃残片补成平行四边形”?
A
B
C
教学过程分析
已知: ABC
△
求作:平行四边形ABCD,使它的三个顶点分别是A、B、C.
A
B
C
A
B
C
教学过程分析
C
方案1
A
B
A
B
C
方案2
A
B
C
A
B
C
方案3
方案4
D
D
D
D
AB∥CD,AD∥BC
AB=CD,AD=BC
OA=OC,OB=OD
AB CD
∥
﹦
两组对边分别相等的四边形是平行四边形
已知:在四边形ABCD中,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
分析:四边形ABCD是平行四边形
命题证明
A
B
D
C
AB∥CD AD∥BC
2
1
3
4
∠1=∠2 ∠3=∠4
△ABC≌△CDA
对角线互相平分的四边形是平行四边形.
方案(3)证明
A
B
C
D
教学过程分析
判定平行四边形的方法:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2)判定定理1:两组对边分别相等的四边形是平行四边形;
(3)判定定理2:对角线互相平分的四边形是平行四边形.
归纳
教学过程分析
例1.如图所示,四边形ABCD中,
(1)若AB//CD,补充条件_________,使四边形ABCD为平
行四边形.
(2)若AB=CD,补充条件________,使四边形ABCD为平
行四边形.
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,补
充条件__________,使四边形ABCD为平行四边形.
A
B
C
D
O
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
分析:
方法1:要证四边形BFDE是平行四边形,先证BO=DO,EO=FO
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF.。求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
分析:
方法2:要证四边形BFDE是平行四边形,可先证BE=DF,BF=DE,从而又需证△ABE≌△CDF ,△ADE≌△CBF
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
BE=DF
变式1
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
变式2
BE⊥AC, DF⊥AC
1.在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=___ cm, DO= ____cm时,四边形ABCD为平行四边形.
2、在下列条件中,不能判定四边形是平行四边形的
是( )
(A) AB∥CD,AD∥BC (B) AB=CD,AD=BC
(C) AB∥CD,AD=BC (D) AB∥CD, ∠A=∠C
3、如图(1),AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
4、已知:如图(2),ABCD中,点E、F分别在
CD、AB上,DF∥BE,EF交BD于点O.
求证:EO=OF.
F
A
B
C
D
E
(1)
C
A
D
F
B
E
O
(2)
说说你的 收获
教学过程分析
教学过程分析
必做题:教材P91第4、5题
选做题:
如图所示,在 ABC中,D是BC边的中点,F、E分别是AD及其延长线上的点,CF∥BE.
(1)求证: BDE≌ CDF
(2)请连结BF,CE,试判断四边形BECF
是何种特殊四边形?并说明理由.
△
△
△
A
B
C
D
E
F
教材分析
过程分析
评价分析
目的分析
教法分析
1、通过例题讲解和习题训练,从识记、掌握、运用、迁移四方面评价学生的学习结果;
2、通过动手实践、小组讨论、上
台发言来观察学生学习数学的水平,
观察他们的数学思维能力;
3、关注学生表现出来的心理情绪和态度,是否对学习数学有浓厚的兴趣。
过程分析
目的分析
教法分析
评价分析
教材分析
(一)教材的地位和作用
1、是平行线和全等三角形知识的应用和延伸;
2、对其他的特殊四边形的判定定理具有指导意义,为学习其他特殊四边形判定定理奠定基础;
3、便于学生弄清平行四边形和其他特殊平行四边形的特性、共性及他们之间的从属关系.
教材分析
过程分析
目的分析
教法分析
评价分析
重点:
平行四边形的判定定理及其 运用.
难点:判定定理的推导过程.
教材分析
过程分析
目的分析
教法分析
评价分析
教材分析
过程分析
目的分析
教法分析
评价分析
2、方法与过程:探索由三角形补成平行四边形的方法,由此发现平行四边形的判定.
3、情感态度价值观:经过自主探索和合作交流,敢于发表自己的观点,能从交流中获益.
1、知识与技能:掌握平行四边形判定定理,并会运用判定定理解决相关问题.
教材分析
过程分析
教法分析
目的分析
评价分析
情境教学法 课堂研讨法
1、培养学生的自学能力;
2、落实学生的主体地位,促进学生的主动发展;
3、为培养学生的创新意识与创新能力奠定基础.
教材分析
过程分析
教法分析
目的分析
评价分析
1、指导学生如何将实际问题转化为数学问题,明白数学与人类的密切关系;
2、指导学生通过类比、联想、推理等思维进行数学研究;
3、明白动手实践,自主探索、合作交流是我们学习的重要方式;明白现代信息技术的发展对我们数学有着重大的帮助.
教材分析
过程分析
目的分析
教法分析
评价分析
创设情境
启发探究
引导落实
小结深化
课堂小结
接受挑战
启迪思维
完成作答
实际应用
建构认知
教师指导过程
学生学习过程
教学过程分析
(1)复习平行四边形定义、性质
教学过程分析
(2)上演小话剧:一位男生不小心把老师的平行四边形玻璃教具打裂,剩下最大的一块保留了平行四边形的三个顶点,这名同学拿到玻璃店,却无法复制一块原模原样的,该生一筹莫展。提出问题“如何把三角形的玻璃残片补成平行四边形”?
A
B
C
教学过程分析
已知: ABC
△
求作:平行四边形ABCD,使它的三个顶点分别是A、B、C.
A
B
C
A
B
C
教学过程分析
C
方案1
A
B
A
B
C
方案2
A
B
C
A
B
C
方案3
方案4
D
D
D
D
AB∥CD,AD∥BC
AB=CD,AD=BC
OA=OC,OB=OD
AB CD
∥
﹦
两组对边分别相等的四边形是平行四边形
已知:在四边形ABCD中,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
分析:四边形ABCD是平行四边形
命题证明
A
B
D
C
AB∥CD AD∥BC
2
1
3
4
∠1=∠2 ∠3=∠4
△ABC≌△CDA
对角线互相平分的四边形是平行四边形.
方案(3)证明
A
B
C
D
教学过程分析
判定平行四边形的方法:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2)判定定理1:两组对边分别相等的四边形是平行四边形;
(3)判定定理2:对角线互相平分的四边形是平行四边形.
归纳
教学过程分析
例1.如图所示,四边形ABCD中,
(1)若AB//CD,补充条件_________,使四边形ABCD为平
行四边形.
(2)若AB=CD,补充条件________,使四边形ABCD为平
行四边形.
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,补
充条件__________,使四边形ABCD为平行四边形.
A
B
C
D
O
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
分析:
方法1:要证四边形BFDE是平行四边形,先证BO=DO,EO=FO
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF.。求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
分析:
方法2:要证四边形BFDE是平行四边形,可先证BE=DF,BF=DE,从而又需证△ABE≌△CDF ,△ADE≌△CBF
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
BE=DF
变式1
教学过程分析
例2 已知:平行四边形ABCD的对角线AC,BC相交于点O,E、F是AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形.
C
B
D
A
E
F
O
变式2
BE⊥AC, DF⊥AC
1.在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC= ___ cm, CD= ____cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=___ cm, DO= ____cm时,四边形ABCD为平行四边形.
2、在下列条件中,不能判定四边形是平行四边形的
是( )
(A) AB∥CD,AD∥BC (B) AB=CD,AD=BC
(C) AB∥CD,AD=BC (D) AB∥CD, ∠A=∠C
3、如图(1),AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
4、已知:如图(2),ABCD中,点E、F分别在
CD、AB上,DF∥BE,EF交BD于点O.
求证:EO=OF.
F
A
B
C
D
E
(1)
C
A
D
F
B
E
O
(2)
说说你的 收获
教学过程分析
教学过程分析
必做题:教材P91第4、5题
选做题:
如图所示,在 ABC中,D是BC边的中点,F、E分别是AD及其延长线上的点,CF∥BE.
(1)求证: BDE≌ CDF
(2)请连结BF,CE,试判断四边形BECF
是何种特殊四边形?并说明理由.
△
△
△
A
B
C
D
E
F
教材分析
过程分析
评价分析
目的分析
教法分析
1、通过例题讲解和习题训练,从识记、掌握、运用、迁移四方面评价学生的学习结果;
2、通过动手实践、小组讨论、上
台发言来观察学生学习数学的水平,
观察他们的数学思维能力;
3、关注学生表现出来的心理情绪和态度,是否对学习数学有浓厚的兴趣。
