1.4矩形的性质
图片预览




文档简介
(共24张PPT)
班级----我的家---全靠
我
他
你
你预习了吗???
1.4矩形的性质
咱们 是最棒的!我能行!!!
动动脑,回忆一下平行四边形的定义和性质
定义:________________
的四边形叫做平行四边形;
性质:
(1)平行四边形的两组对边______;
(2)平行四边形的两组对角_______;
(3)平行四边形的对角线_________;
两组对边分别平行
平行且相等
相等
互相平分
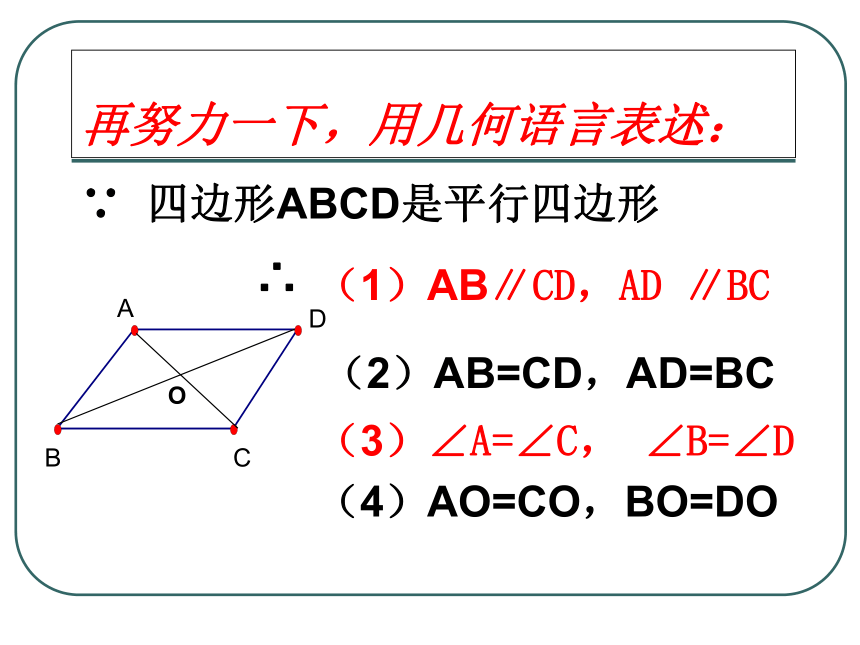
再努力一下,用几何语言表述:
(1)AB∥CD,AD ∥BC
(2)AB=CD,AD=BC
(3)∠A=∠C, ∠B=∠D
(4)AO=CO,BO=DO
O
∵ 四边形ABCD是平行四边形
∴
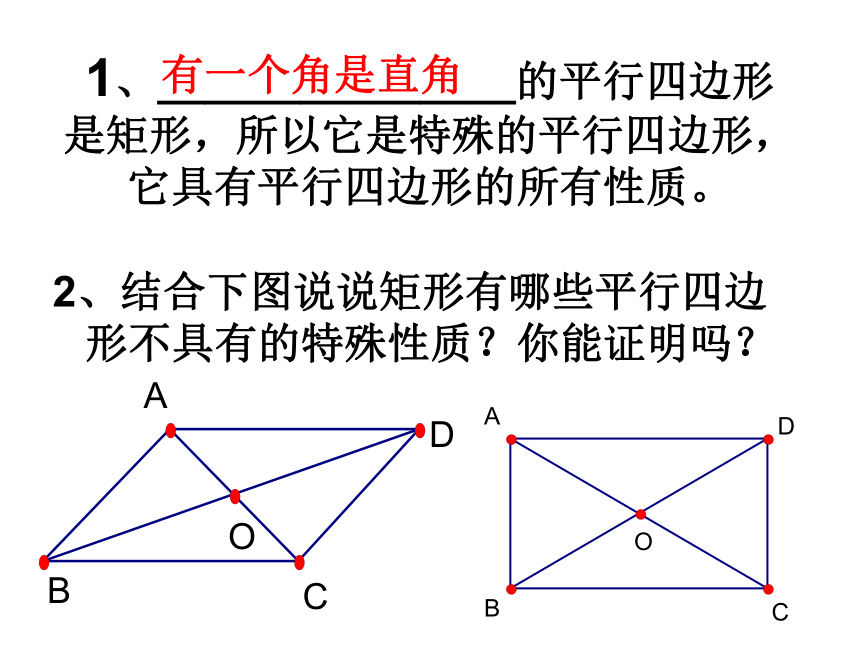
1、_______________的平行四边形是矩形,所以它是特殊的平行四边形,它具有平行四边形的所有性质。
2、结合下图说说矩形有哪些平行四边形不具有的特殊性质?你能证明吗?
有一个角是直角
矩形性质
定理一:矩形四个角都是直角。
定理二:矩形对角线相等相等且相
互平分。
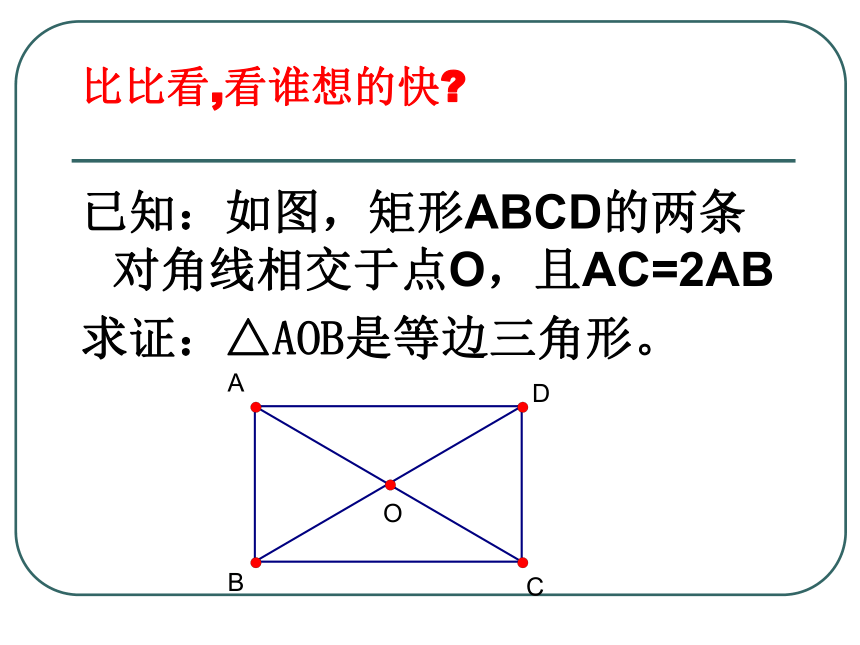
比比看,看谁想的快
已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB
求证:△AOB是等边三角形。
等边三角形的判定
定义:三边都_____三角形叫做等边三角形;
三个角都______的三角形是等边三角形;
有两个角是_____的三角形是等边三角形;
有一个角是600的______三角形是等边三角形;
比比看,看谁想的快
已知:矩形ABCD的两条对角线相交 于点O,且∠AOD=1200,AB=4cm
求矩形对角线的长
1200
已知:如图,矩形ABCD中,点F 是BC上的一点,且DF=BC, AE⊥DF于点E,
求证:BF=EF
矩形ABCD的两条对角线相交于点O,观察图中的Rt△ABC,你能发现它有什么性质
提示:OA=OB=OC
由此你可以得到什么结论吗?
结论:直角三角形斜边上的中线等于 斜边的一半。
它的逆命题是什么?你能证明吗?
如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形
你能证明此结论吗?
D
你还有新的方法吗?
A
C
B
D
在AB上取点D,
使DC=BD
推理过程的书写格式:
(1)∵BO是Rt△ABC斜边上的中线
∴BO=___ ( )
(2)∵ OB是△ABC的中线,且OB=
∴ ________________
已知:如图,BD、CE是△ABC的两条高,M是BC的中点,求证:ME=MD
已知:如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F,G、H分别是AD、BC的中点,
求证:EG=FH,EG∥FH
已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E为矩ABCD外一点,且AE⊥CE,
求证:BE⊥DE
提高训练
如图 在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
如果FE⊥AE,求证FE=AE。
②如果FE=AE 你能证明FE⊥AE?
小结一下吧.
定义:
________的平行四边形叫做矩形;
性质:
矩形的四个角_____________;
矩形的对角线_____________;
定理:
直角三角形斜边上的中线等于斜边的一半
如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形
咱们的目标:
永争第一
班级----我的家---全靠
我
他
你
你预习了吗???
1.4矩形的性质
咱们 是最棒的!我能行!!!
动动脑,回忆一下平行四边形的定义和性质
定义:________________
的四边形叫做平行四边形;
性质:
(1)平行四边形的两组对边______;
(2)平行四边形的两组对角_______;
(3)平行四边形的对角线_________;
两组对边分别平行
平行且相等
相等
互相平分
再努力一下,用几何语言表述:
(1)AB∥CD,AD ∥BC
(2)AB=CD,AD=BC
(3)∠A=∠C, ∠B=∠D
(4)AO=CO,BO=DO
O
∵ 四边形ABCD是平行四边形
∴
1、_______________的平行四边形是矩形,所以它是特殊的平行四边形,它具有平行四边形的所有性质。
2、结合下图说说矩形有哪些平行四边形不具有的特殊性质?你能证明吗?
有一个角是直角
矩形性质
定理一:矩形四个角都是直角。
定理二:矩形对角线相等相等且相
互平分。
比比看,看谁想的快
已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB
求证:△AOB是等边三角形。
等边三角形的判定
定义:三边都_____三角形叫做等边三角形;
三个角都______的三角形是等边三角形;
有两个角是_____的三角形是等边三角形;
有一个角是600的______三角形是等边三角形;
比比看,看谁想的快
已知:矩形ABCD的两条对角线相交 于点O,且∠AOD=1200,AB=4cm
求矩形对角线的长
1200
已知:如图,矩形ABCD中,点F 是BC上的一点,且DF=BC, AE⊥DF于点E,
求证:BF=EF
矩形ABCD的两条对角线相交于点O,观察图中的Rt△ABC,你能发现它有什么性质
提示:OA=OB=OC
由此你可以得到什么结论吗?
结论:直角三角形斜边上的中线等于 斜边的一半。
它的逆命题是什么?你能证明吗?
如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形
你能证明此结论吗?
D
你还有新的方法吗?
A
C
B
D
在AB上取点D,
使DC=BD
推理过程的书写格式:
(1)∵BO是Rt△ABC斜边上的中线
∴BO=___ ( )
(2)∵ OB是△ABC的中线,且OB=
∴ ________________
已知:如图,BD、CE是△ABC的两条高,M是BC的中点,求证:ME=MD
已知:如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F,G、H分别是AD、BC的中点,
求证:EG=FH,EG∥FH
已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E为矩ABCD外一点,且AE⊥CE,
求证:BE⊥DE
提高训练
如图 在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
如果FE⊥AE,求证FE=AE。
②如果FE=AE 你能证明FE⊥AE?
小结一下吧.
定义:
________的平行四边形叫做矩形;
性质:
矩形的四个角_____________;
矩形的对角线_____________;
定理:
直角三角形斜边上的中线等于斜边的一半
如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形
咱们的目标:
永争第一
