《11.3多边形及其内角和》同步优生辅导训练(附答案)2021-2022学年八年级数学人教版上册
文档属性
| 名称 | 《11.3多边形及其内角和》同步优生辅导训练(附答案)2021-2022学年八年级数学人教版上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 00:00:00 | ||
图片预览

文档简介
2021-2022学年人教版八年级数学上册《11.3多边形及其内角和》
同步优生辅导训练(附答案)
1.已知某个正多边形的一个外角为40°,这个正多边形内角和等于( )
A.1080° B.1260° C.1440° D.1620°
2.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
3.可以作为某一个多边形内角和度数的是( )
A.320° B.720° C.1000° D.2180°
4.如图,四边形ABCD中,∠1、∠2、∠3分别为∠BAD、∠ABC、∠BCD的外角,下列判断正确的是( )
A.∠1+∠3=∠ABC+∠D B.∠1+∠3=180°
C.∠2=∠D D.∠1+∠2+∠3=360°
5.如图,点A、B、C、D、E在同一平面内连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )
A.220° B.240° C.260° D.280°
6.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )A.10 B.11 C.12 D.10或11或12
7.如图,把△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=108°,∠C=35°,则∠2的度数为( )
A.35° B.36° C.37° D.38°
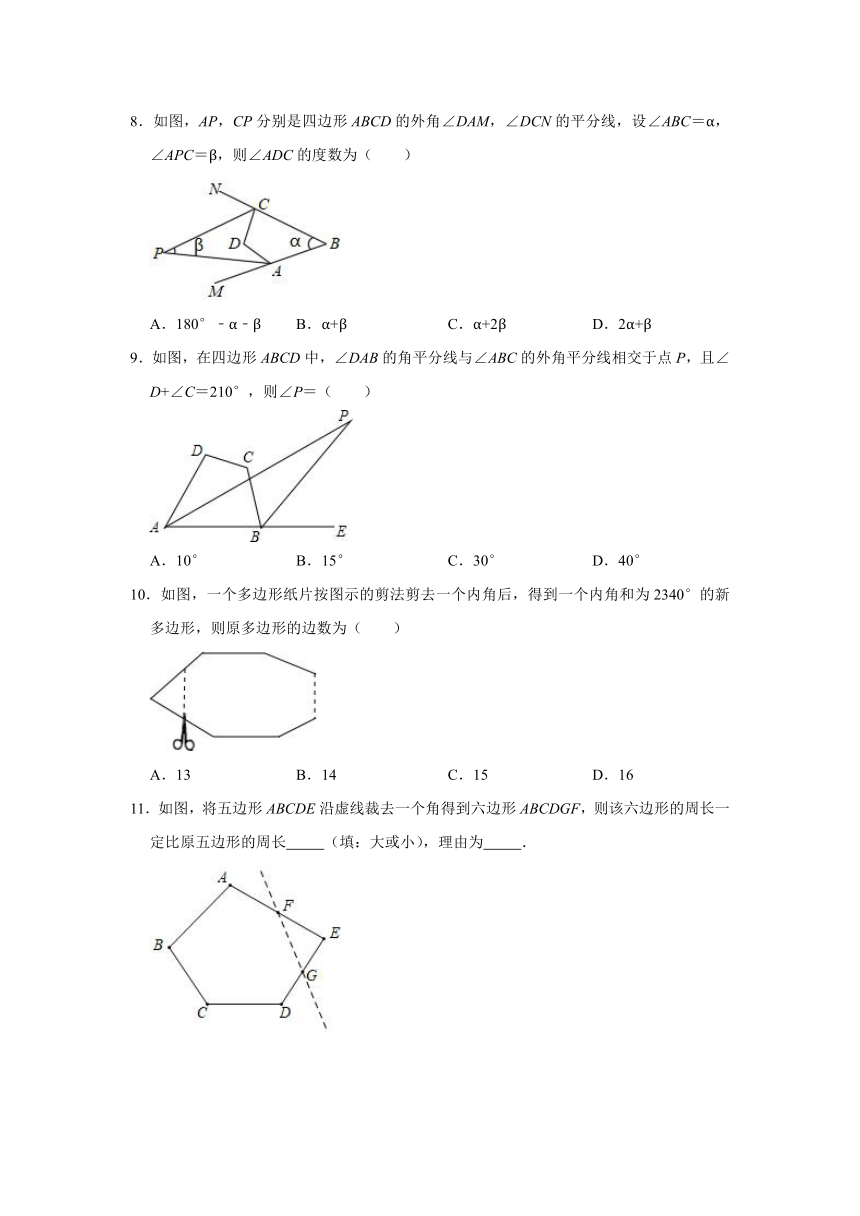
8.如图,AP,CP分别是四边形ABCD的外角∠DAM,∠DCN的平分线,设∠ABC=α,∠APC=β,则∠ADC的度数为( )
A.180°﹣α﹣β B.α+β C.α+2β D.2α+β
9.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=( )
A.10° B.15° C.30° D.40°
10.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
A.13 B.14 C.15 D.16
11.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
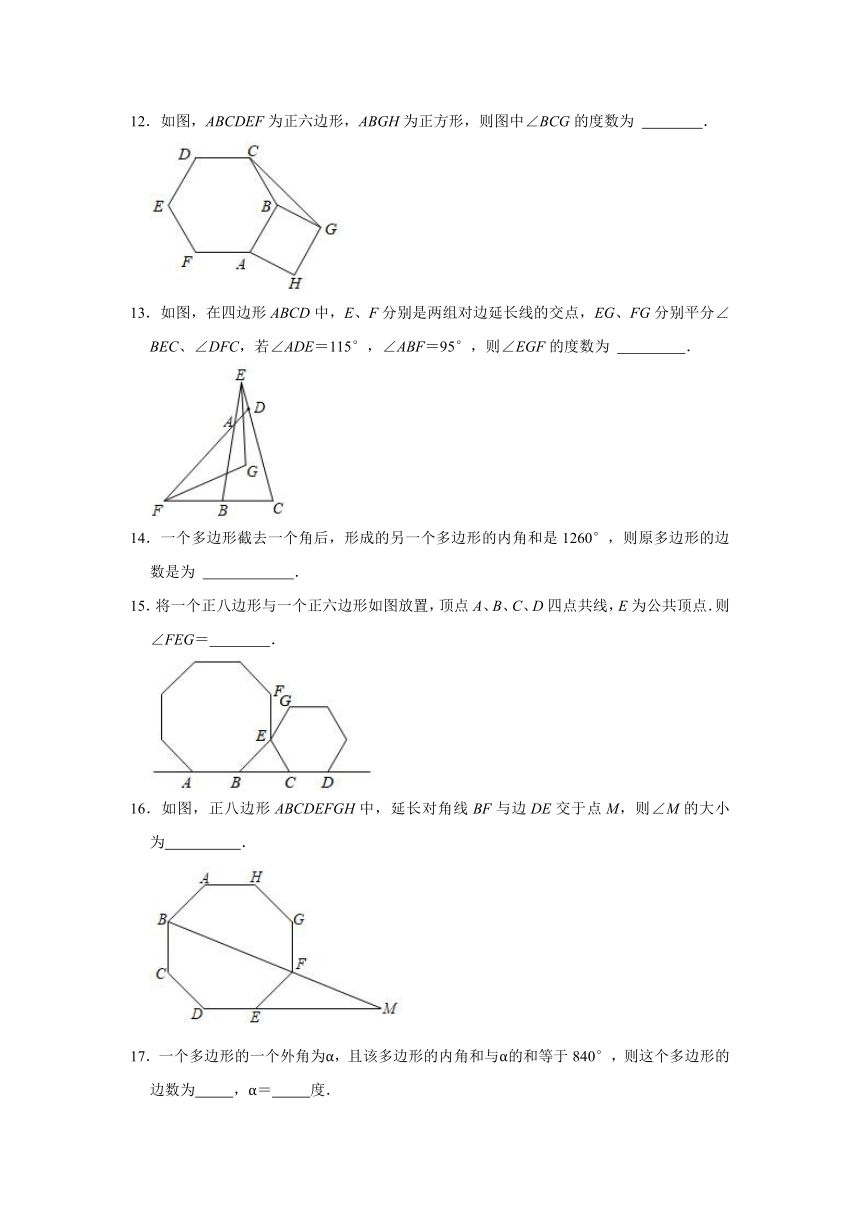
12.如图,ABCDEF为正六边形,ABGH为正方形,则图中∠BCG的度数为 .
13.如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADE=115°,∠ABF=95°,则∠EGF的度数为 .
14.一个多边形截去一个角后,形成的另一个多边形的内角和是1260°,则原多边形的边数是为 .
15.将一个正八边形与一个正六边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠FEG= .
16.如图,正八边形ABCDEFGH中,延长对角线BF与边DE交于点M,则∠M的大小为 .
17.一个多边形的一个外角为α,且该多边形的内角和与α的和等于840°,则这个多边形的边数为 ,α= 度.
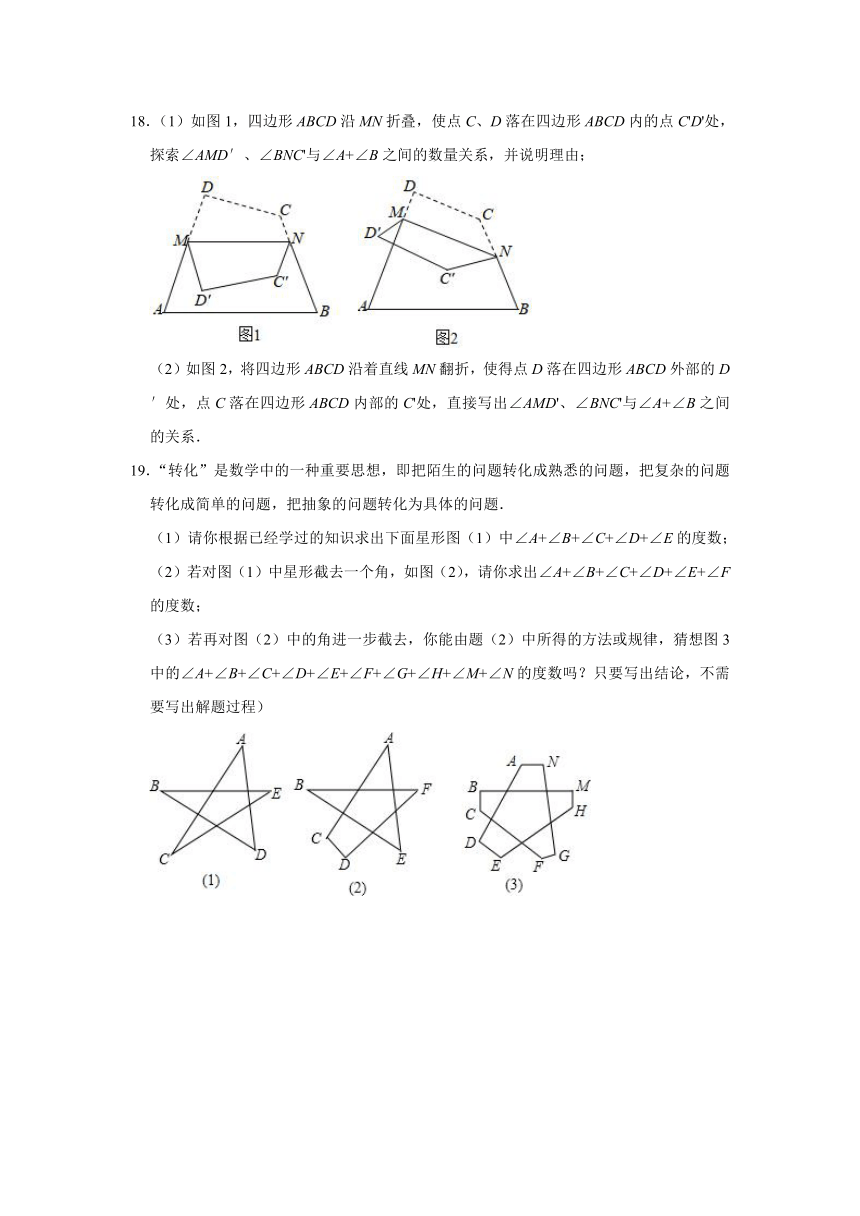
18.(1)如图1,四边形ABCD沿MN折叠,使点C、D落在四边形ABCD内的点C'D'处,探索∠AMD′、∠BNC'与∠A+∠B之间的数量关系,并说明理由;
(2)如图2,将四边形ABCD沿着直线MN翻折,使得点D落在四边形ABCD外部的D′处,点C落在四边形ABCD内部的C'处,直接写出∠AMD'、∠BNC'与∠A+∠B之间的关系.
19.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
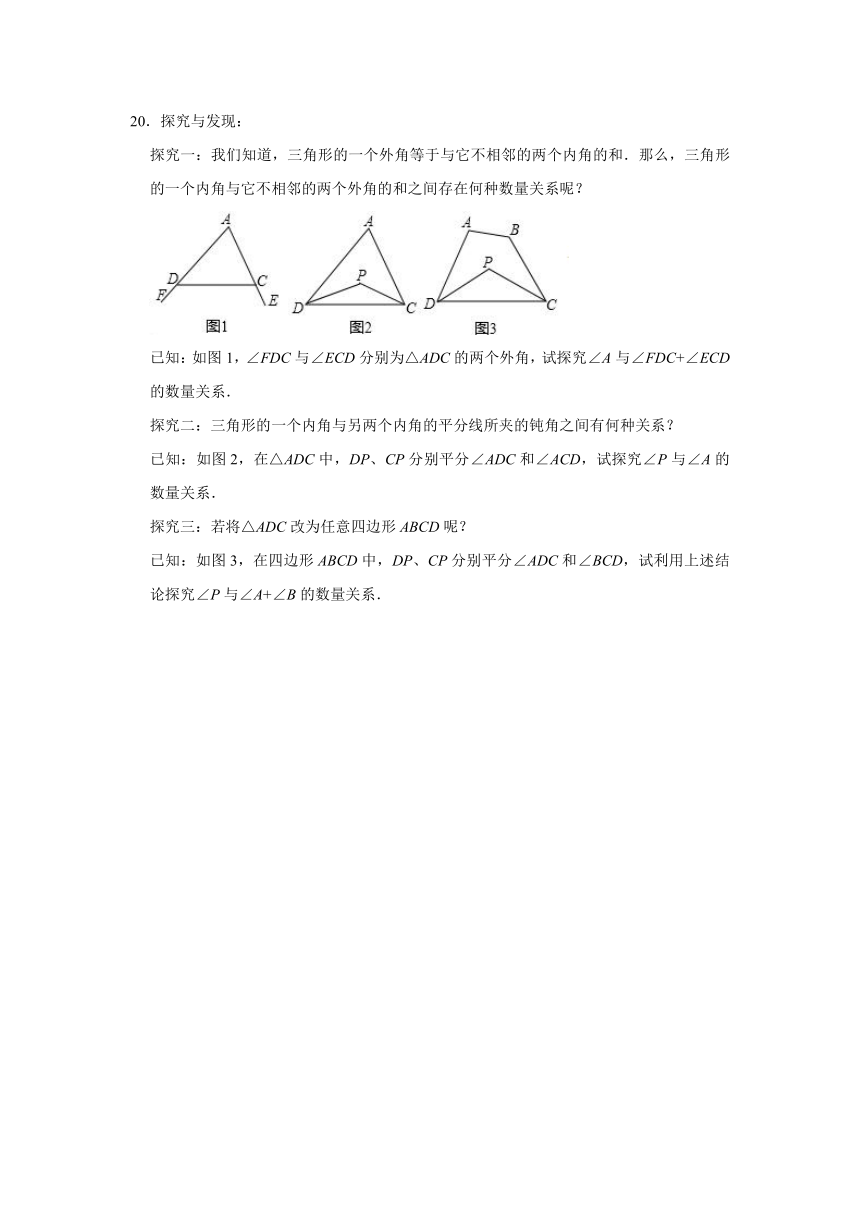
20.探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
参考答案
1.解:正多边形的每个外角相等,且其和为360°,
据此可得,
解得n=9.
(9﹣2)×180°=1260°,
即这个正多边形的内角和为1260°.
故选:B.
2.解:设所求多边形边数为n,
则(n﹣2)?180°=3×360°﹣180°,
解得n=7.
故选:C.
3.解:∵多边形内角和公式为(n﹣2)×180,
∴多边形内角和一定是180的倍数,
∵720°=4×180°,
故选:B.
4.解:∵∠1+∠DAB=180°,∠3+∠BCD=180°,
∴∠1+∠3+∠DAB+∠BCD=360°,
∵∠ABC+∠BCD+∠D+∠DAB=360°,
∴∠1+∠3=∠ABC+∠D,
故A符合题意;
∵∠1+∠3只有∠ABC和∠D互补时才等于180°,
故B不符合题意;
∵只有∠ABC和∠D互补时,∠2=∠D,
故C不符合题意;
∵多边形的外角和是360°,
∴∠1+∠2+∠3<360°,
故D不符合题意;
故选:A.
5.解:连接BD,
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
故选:D.
6.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
7.解:如图,设C′D与AC交于点O,
∵∠C=35°,
∴∠C′=∠C=35°,
∵∠1=∠DOC+∠C,∠1=108°,
∴∠DOC=∠1﹣∠C=108°﹣35°=73°,
∵∠DOC=∠2+∠C′,
∴∠2=∠DOC﹣∠C′=73°﹣35°=38°.
故选:D.
8.解:在四边形ABCD中,
∠ADC=360°﹣α﹣(∠DCB+∠DAB)
=360°﹣α﹣(360°﹣2∠PCD﹣2∠PAD)
=2(∠PCD+∠PAD)﹣α
=2(∠ADC﹣β)﹣α,
∴∠ADC=α+2β,
故选:C.
9.解:如图,∵∠D+∠C=210°,∠DAB+∠ABC+∠C+∠D=360°,
∴∠DAB+∠ABC=150°.
又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,
∴∠PAB+∠ABP=∠DAB+∠ABC+(180°﹣∠ABC)=90°+(∠DAB+∠ABC)=165°,
∴∠P=180°﹣(∠PAB+∠ABP)=15°.
故选:B.
10.解:设新多边形是n边形,由多边形内角和公式得
(n﹣2)180°=2340°,
解得n=15,
原多边形是15﹣1=14,
故选:B.
11.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
12.解:∵ABCDEF为正六边形,ABGH为正方形,
∴AB=BC=BG,
∴∠BCG=∠BGC,
∵正六边形ABCDEF的每一个内角是4×180°÷6=120°,
正方形ABGH的每个内角是90°,
∴∠CBG=360°﹣120°﹣90°=150°,
∴∠BCG+∠BGC=180°﹣150°=30°,
∴∠BCG=15°.
故答案为:15°.
13.解:如图:
连接EF,根据三角形内角和定理及角平分线的性质得:
∠EGF=180°﹣(∠GEF+∠GFE)=180°﹣(∠CEF﹣∠CEG+∠CFE﹣CFG)
=180°﹣(∠CEF+∠CFE)+(∠CFG+∠CEG)
=∠C+∠CFD+∠CEB
=∠C+(180°﹣∠C﹣∠CDF)+(180°﹣∠C﹣∠CBE)
=∠C+180°﹣∠C﹣(180°﹣115°+180°﹣95°)
=105°.
故答案为:105°.
14.解:设截去一个角后,多边形的边数为n,
由题意得(n﹣2)×180°=1260°,
解得n=9.
因为多边形截去一角后边数可能不变,可能增加1,可能减小1,
∴原多边形可能为8或9或10.
故答案为:8或9或10.
15.解:由多边形的内角和可得,
∠ABE=∠BEF=,
∴∠EBC=180°﹣∠ABE=180°﹣135°=45°,
∵∠DCE=∠CEG=,
∴∠BCE=180°﹣∠DCE=60°,
由三角形的内角和得:
∠BEC=180°﹣∠EBC﹣∠BCE=180°﹣45°﹣60°=75°,
∴∠FEG=360°﹣∠BEF﹣∠CEG﹣∠BEC
=360°﹣135°﹣120°﹣75°
=30°.
故答案为:30°.
16.解:∵八边形ABCDEFGH是正八边形,
∴∠DEF=(8﹣2)×180°÷8=135°,
∴∠FEM=45°,
∴∠DEF=∠EFG,
∵BF平分∠EFG,
∴∠EFB=∠BFE==67.5°,
∵∠BFE=∠FEM+∠M,
∴∠M=∠BFE﹣∠FEM,
∴∠M=22.5°.
故答案为:22.5°.
17.解:∵840÷180=4…120,
∴这个多边形的边数为:4+2=6,
α=120°,
故答案为:六;120.
18.解:(1)∠AMD′+∠BNC′=360°﹣2(∠A+∠B),理由如下:
根据四边形的内角和为360°可知,∠D+∠C=360°﹣(∠A+∠B),
∠DMN+∠CNM=360°﹣(∠C+∠D)=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠DMD′+∠CNC′=2(∠A+∠B),
∵∠DMD′+∠AMD′=180°,∠CNC′+∠BNC′=180°,
∴∠AMD′+∠BNC′=360°﹣2(∠A+∠B).
(2)∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B),理由如下:
由(1)知,∠DMN+∠CNM=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠D′MN+∠C′NM=∠A+∠B,
由四边形的内角和为360°得,∠D′MN﹣∠AMD′+∠BNC′+∠C′NM=360°﹣(∠A+∠B)
∴∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B).
19.解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
20.解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠ACD
=180°﹣(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B).
同步优生辅导训练(附答案)
1.已知某个正多边形的一个外角为40°,这个正多边形内角和等于( )
A.1080° B.1260° C.1440° D.1620°
2.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
3.可以作为某一个多边形内角和度数的是( )
A.320° B.720° C.1000° D.2180°
4.如图,四边形ABCD中,∠1、∠2、∠3分别为∠BAD、∠ABC、∠BCD的外角,下列判断正确的是( )
A.∠1+∠3=∠ABC+∠D B.∠1+∠3=180°
C.∠2=∠D D.∠1+∠2+∠3=360°
5.如图,点A、B、C、D、E在同一平面内连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )
A.220° B.240° C.260° D.280°
6.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )A.10 B.11 C.12 D.10或11或12
7.如图,把△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=108°,∠C=35°,则∠2的度数为( )
A.35° B.36° C.37° D.38°
8.如图,AP,CP分别是四边形ABCD的外角∠DAM,∠DCN的平分线,设∠ABC=α,∠APC=β,则∠ADC的度数为( )
A.180°﹣α﹣β B.α+β C.α+2β D.2α+β
9.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=( )
A.10° B.15° C.30° D.40°
10.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为( )
A.13 B.14 C.15 D.16
11.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
12.如图,ABCDEF为正六边形,ABGH为正方形,则图中∠BCG的度数为 .
13.如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADE=115°,∠ABF=95°,则∠EGF的度数为 .
14.一个多边形截去一个角后,形成的另一个多边形的内角和是1260°,则原多边形的边数是为 .
15.将一个正八边形与一个正六边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠FEG= .
16.如图,正八边形ABCDEFGH中,延长对角线BF与边DE交于点M,则∠M的大小为 .
17.一个多边形的一个外角为α,且该多边形的内角和与α的和等于840°,则这个多边形的边数为 ,α= 度.
18.(1)如图1,四边形ABCD沿MN折叠,使点C、D落在四边形ABCD内的点C'D'处,探索∠AMD′、∠BNC'与∠A+∠B之间的数量关系,并说明理由;
(2)如图2,将四边形ABCD沿着直线MN翻折,使得点D落在四边形ABCD外部的D′处,点C落在四边形ABCD内部的C'处,直接写出∠AMD'、∠BNC'与∠A+∠B之间的关系.
19.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
20.探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
参考答案
1.解:正多边形的每个外角相等,且其和为360°,
据此可得,
解得n=9.
(9﹣2)×180°=1260°,
即这个正多边形的内角和为1260°.
故选:B.
2.解:设所求多边形边数为n,
则(n﹣2)?180°=3×360°﹣180°,
解得n=7.
故选:C.
3.解:∵多边形内角和公式为(n﹣2)×180,
∴多边形内角和一定是180的倍数,
∵720°=4×180°,
故选:B.
4.解:∵∠1+∠DAB=180°,∠3+∠BCD=180°,
∴∠1+∠3+∠DAB+∠BCD=360°,
∵∠ABC+∠BCD+∠D+∠DAB=360°,
∴∠1+∠3=∠ABC+∠D,
故A符合题意;
∵∠1+∠3只有∠ABC和∠D互补时才等于180°,
故B不符合题意;
∵只有∠ABC和∠D互补时,∠2=∠D,
故C不符合题意;
∵多边形的外角和是360°,
∴∠1+∠2+∠3<360°,
故D不符合题意;
故选:A.
5.解:连接BD,
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
故选:D.
6.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
7.解:如图,设C′D与AC交于点O,
∵∠C=35°,
∴∠C′=∠C=35°,
∵∠1=∠DOC+∠C,∠1=108°,
∴∠DOC=∠1﹣∠C=108°﹣35°=73°,
∵∠DOC=∠2+∠C′,
∴∠2=∠DOC﹣∠C′=73°﹣35°=38°.
故选:D.
8.解:在四边形ABCD中,
∠ADC=360°﹣α﹣(∠DCB+∠DAB)
=360°﹣α﹣(360°﹣2∠PCD﹣2∠PAD)
=2(∠PCD+∠PAD)﹣α
=2(∠ADC﹣β)﹣α,
∴∠ADC=α+2β,
故选:C.
9.解:如图,∵∠D+∠C=210°,∠DAB+∠ABC+∠C+∠D=360°,
∴∠DAB+∠ABC=150°.
又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,
∴∠PAB+∠ABP=∠DAB+∠ABC+(180°﹣∠ABC)=90°+(∠DAB+∠ABC)=165°,
∴∠P=180°﹣(∠PAB+∠ABP)=15°.
故选:B.
10.解:设新多边形是n边形,由多边形内角和公式得
(n﹣2)180°=2340°,
解得n=15,
原多边形是15﹣1=14,
故选:B.
11.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
12.解:∵ABCDEF为正六边形,ABGH为正方形,
∴AB=BC=BG,
∴∠BCG=∠BGC,
∵正六边形ABCDEF的每一个内角是4×180°÷6=120°,
正方形ABGH的每个内角是90°,
∴∠CBG=360°﹣120°﹣90°=150°,
∴∠BCG+∠BGC=180°﹣150°=30°,
∴∠BCG=15°.
故答案为:15°.
13.解:如图:
连接EF,根据三角形内角和定理及角平分线的性质得:
∠EGF=180°﹣(∠GEF+∠GFE)=180°﹣(∠CEF﹣∠CEG+∠CFE﹣CFG)
=180°﹣(∠CEF+∠CFE)+(∠CFG+∠CEG)
=∠C+∠CFD+∠CEB
=∠C+(180°﹣∠C﹣∠CDF)+(180°﹣∠C﹣∠CBE)
=∠C+180°﹣∠C﹣(180°﹣115°+180°﹣95°)
=105°.
故答案为:105°.
14.解:设截去一个角后,多边形的边数为n,
由题意得(n﹣2)×180°=1260°,
解得n=9.
因为多边形截去一角后边数可能不变,可能增加1,可能减小1,
∴原多边形可能为8或9或10.
故答案为:8或9或10.
15.解:由多边形的内角和可得,
∠ABE=∠BEF=,
∴∠EBC=180°﹣∠ABE=180°﹣135°=45°,
∵∠DCE=∠CEG=,
∴∠BCE=180°﹣∠DCE=60°,
由三角形的内角和得:
∠BEC=180°﹣∠EBC﹣∠BCE=180°﹣45°﹣60°=75°,
∴∠FEG=360°﹣∠BEF﹣∠CEG﹣∠BEC
=360°﹣135°﹣120°﹣75°
=30°.
故答案为:30°.
16.解:∵八边形ABCDEFGH是正八边形,
∴∠DEF=(8﹣2)×180°÷8=135°,
∴∠FEM=45°,
∴∠DEF=∠EFG,
∵BF平分∠EFG,
∴∠EFB=∠BFE==67.5°,
∵∠BFE=∠FEM+∠M,
∴∠M=∠BFE﹣∠FEM,
∴∠M=22.5°.
故答案为:22.5°.
17.解:∵840÷180=4…120,
∴这个多边形的边数为:4+2=6,
α=120°,
故答案为:六;120.
18.解:(1)∠AMD′+∠BNC′=360°﹣2(∠A+∠B),理由如下:
根据四边形的内角和为360°可知,∠D+∠C=360°﹣(∠A+∠B),
∠DMN+∠CNM=360°﹣(∠C+∠D)=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠DMD′+∠CNC′=2(∠A+∠B),
∵∠DMD′+∠AMD′=180°,∠CNC′+∠BNC′=180°,
∴∠AMD′+∠BNC′=360°﹣2(∠A+∠B).
(2)∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B),理由如下:
由(1)知,∠DMN+∠CNM=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠D′MN+∠C′NM=∠A+∠B,
由四边形的内角和为360°得,∠D′MN﹣∠AMD′+∠BNC′+∠C′NM=360°﹣(∠A+∠B)
∴∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B).
19.解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
20.解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠ACD
=180°﹣(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B).
