2021-2022学年人教版数学七年级上册数学4.3.3余角和补角---同步训练(Word版 含答案)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册数学4.3.3余角和补角---同步训练(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 207.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 10:37:01 | ||
图片预览


文档简介
4.3.3 余角和补角
命题点 1 余角与补角
1.一个角的余角是44°,这个角的补角是 ( )
A.134° B.136° C.156° D.146°
2.将一副三角尺按如图所示的不同方式摆放,则图中∠α与∠β相等的是 ( )
3.[2020·十堰] 如图,将一副三角板重叠放在一起,使直角顶点重合于点O.若∠AOC=130°,则∠BOD等于 ( )
A.30° B.40°
C.50° D.60°
4.已知∠α的补角的一半比∠α小30°,则∠α等于 ( )
A.50° B.60° C.70° D.80°
一个角的余角比它的补角的13还少20°,求这个角的度数.
6.如图,已知∠AOD=150°.
(1)如图(a),∠AOC=∠BOD=90°,则∠BOC的余角是 °,∠BOC= °.?
(2)如图(b),已知∠AOB与∠BOC互为余角.
①若OB平分∠AOD,求∠BOC的度数;
②若∠COD是∠BOC的4倍,求∠BOC的度数.
命题点 2 互余与互补的性质
7.如图,∠EDC=∠CDF=90°,∠1=∠2.
(1)图中哪些角互为余角,哪些角互为补角?
(2)∠ADF与∠BDE有什么数量关系?∠ADC与∠BDC有什么数量关系?为什么?
8.如图,已知∠1+∠2=90°.
(1)若∠2+∠3=90°,则∠1与∠3是什么关系?为什么?
(2)若要使∠2与∠4相等,则∠1与∠4要满足什么关系?为什么?
命题点 3 方向角
9.小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西25°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是 ( )
4029710288290A.左转85° B.右转85°
C.右转95° D.左转95°
如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,那么∠AOB的大小为 °.?
368427043815011.如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;?
(2)若射线OE平分∠COD,求∠AOE的度数.
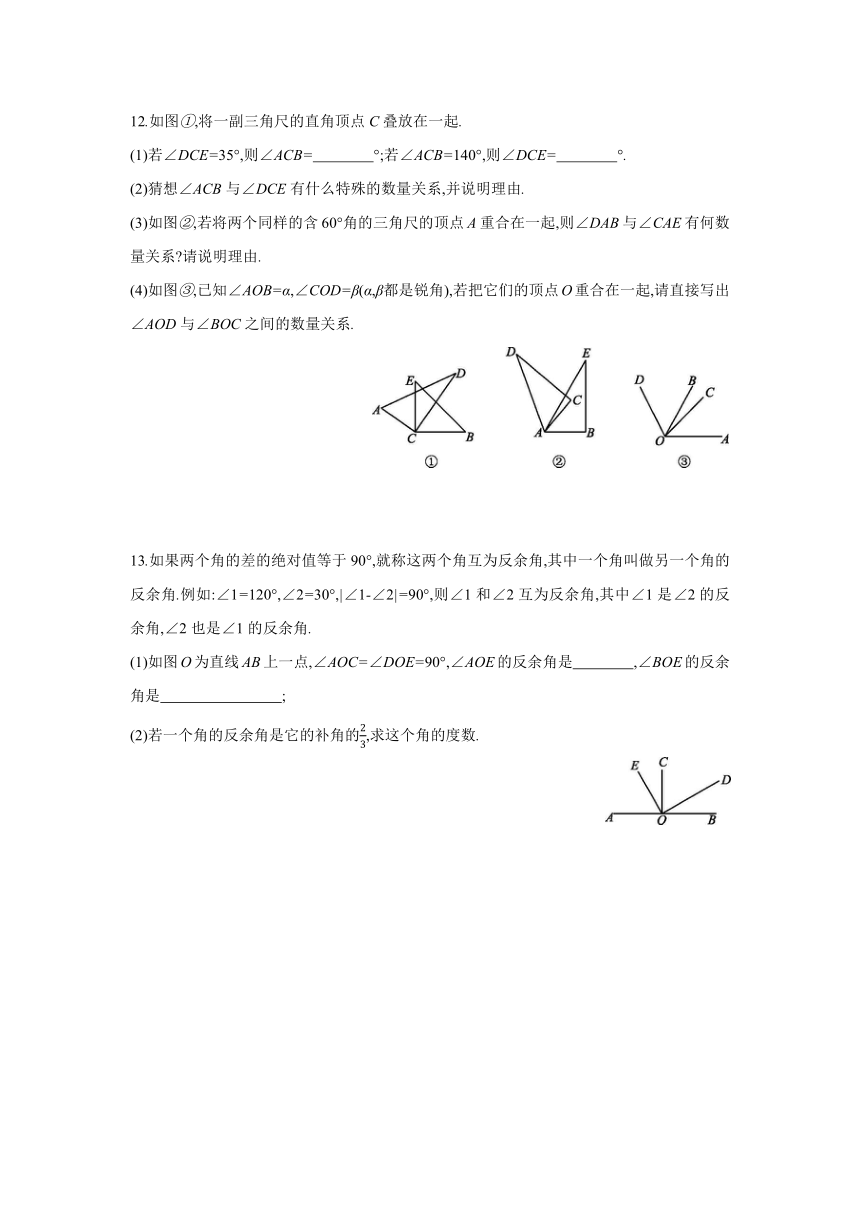
12.如图①,将一副三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,则∠ACB= °;若∠ACB=140°,则∠DCE= °.?
(2)猜想∠ACB与∠DCE有什么特殊的数量关系,并说明理由.
(3)如图②,若将两个同样的含60°角的三角尺的顶点A重合在一起,则∠DAB与∠CAE有何数量关系?请说明理由.
(4)如图③,已知∠AOB=α,∠COD=β(α,β都是锐角),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC之间的数量关系.
13.如果两个角的差的绝对值等于90°,就称这两个角互为反余角,其中一个角叫做另一个角的反余角.例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为反余角,其中∠1是∠2的反余角,∠2也是∠1的反余角.
(1)如图O为直线AB上一点,∠AOC=∠DOE=90°,∠AOE的反余角是 ,∠BOE的反余角是 ;?
(2)若一个角的反余角是它的补角的23,求这个角的度数.
典题讲评与答案详析
1.A [解析] 因为一个角的余角是44°,
所以这个角的度数是90°-44°=46°.
所以这个角的补角是180°-46°=134°.
故选A.
2.D
3.C [解析] 因为∠AOC=130°,
所以∠BOC=∠AOC-∠AOB=40°.
所以∠BOD=∠COD-∠BOC=50°.
故选C.
4.D [解析] 依题意得∠α-12(180°-∠α)=30°,
解得∠α=80°.
故选D.
5.解:设这个角的度数为x,则它的余角为90°-x,补角为180°-x.
根据题意,得90°-x=13(180°-x)-20°,
解得x=75°.
即这个角的度数为75°.
6.解:(1)60 30
[解析] 因为∠AOC=∠BOD=90°,
所以∠BOC+∠AOB=90°,∠BOC+∠COD=90°.
所以∠BOC的余角是∠AOB和∠COD.
因为∠AOD=150°,∠AOC=90°,
所以∠COD=60°.
因为∠BOD=90°,
所以∠BOC=30°.
故答案为60,30.
(2)①因为∠AOB与∠BOC互为余角,
所以∠AOC=∠AOB+∠BOC=90°.
因为OB平分∠AOD,
所以∠AOB=12∠AOD=12×150°=75°.
所以∠BOC=∠AOC-∠AOB=90°-75°=15°.
②由①知∠AOC=90°.
因为∠COD=∠AOD-∠AOC=150°-90°=60°,
且∠COD是∠BOC的4倍,
所以∠BOC=15°.
7.解:(1)因为∠EDC=∠CDF=90°,∠1=∠2,
所以∠1和∠ADC,∠1和∠BDC,∠2和∠ADC,∠2和∠BDC互为余角;
∠1和∠ADF,∠2和∠ADF,∠EDC和∠CDF,∠2和∠BDE,∠1和∠BDE互为补角.
(2)∠ADF=∠BDE,∠ADC=∠BDC.
理由:因为∠1=∠2,∠1+∠ADF=180°,∠2+∠BDE=180°,所以∠ADF=∠BDE.
因为∠EDC=∠CDF=90°,
所以∠1+∠ADC=90°,∠2+∠BDC=90°.
又因为∠1=∠2,
所以∠ADC=∠BDC.
8.解:(1)∠1=∠3.
理由:因为∠1+∠2=90°,∠2+∠3=90°,
所以∠1=∠3.
(2)∠1+∠4=90°.
理由:因为∠1+∠2=90°,∠1+∠4=90°,
所以∠2=∠4.
9.B [解析] 如图:
60°+25°=85°.
由北偏西25°转向北偏东60°,需要向右转85°.
故选B.
10.140 [解析] 因为点A在点O北偏西60°的方向上,
所以OA与表示正西方向的射线的夹角为90°-60°=30°.
又因为点B在点O的南偏东20°的方向上,
所以∠AOB=30°+90°+20°=140°.
故答案为:140.
11.解:(1)如图,因为OB的方向是北偏西40°,OA的方向是北偏东15°,
所以∠FOB=40°,∠FOA=15°.
所以∠AOB=∠FOB+∠FOA=55°.
因为∠AOB=∠AOC,所以∠AOC=55°.
所以∠FOC=∠FOA+∠AOC=70°.
所以OC的方向是北偏东70°.
故答案为北偏东70°.
(2)因为∠AOB=55°,∠AOC=∠AOB=55°,
所以∠BOC=110°.
因为射线OD是OB的反向延长线,
所以∠BOD=180°.
所以∠COD=180°-110°=70°.
因为OE平分∠COD,所以∠COE=35°.
又因为∠AOC=55°,所以∠AOE=90°.
12.解:(1)145 40 [解析] 因为∠ACD=90°,∠DCE=35°,
所以∠ACE=90°-35°=55°.
因为∠BCE=90°,
所以∠ACB=∠ACE+∠BCE=55°+90°=145°.
因为∠ACB=140°,∠BCE=90°,
所以∠ACE=140°-90°=50°.
因为∠ACD=90°,所以∠DCE=90°-50°=40°.
故答案为145,40.
(2)∠ACB+∠DCE=180°.理由如下:
因为∠ACB=∠ACD+∠BCD=90°+∠BCD,
所以∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=90°+90°=180°.
(3)∠DAB+∠CAE=120°.理由如下:
因为∠DAB=∠DAC+∠CAB=60°+∠CAB,
所以∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=60°+60°=120°.
(4)∠AOD+∠BOC=α+β.理由如下:
因为∠AOD=∠COD+∠COA=β+∠COA,
所以∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.
13.解:(1)∠AOD ∠EOC和∠BOD [解析] 因为∠AOD-∠AOE=∠DOE=90°,
所以∠AOE的反余角是∠AOD.
因为∠BOE-∠EOC=∠BOC=180°-∠AOC=90°,∠BOE-∠BOD=∠DOE=90°,
所以∠BOE的反余角为∠EOC和∠BOD.
故答案为∠AOD,∠EOC和∠BOD.
(2)设这个角的度数为x°.
若这个角是锐角,则它的反余角为(90+x)°.
由题意,得90+x=23(180-x),解得x=18.
若这个角是钝角,则它的反余角为(x-90)°.
由题意,得x-90=23(180-x),解得x=126.
综上所述,这个角的度数为18°或126°.
命题点 1 余角与补角
1.一个角的余角是44°,这个角的补角是 ( )
A.134° B.136° C.156° D.146°
2.将一副三角尺按如图所示的不同方式摆放,则图中∠α与∠β相等的是 ( )
3.[2020·十堰] 如图,将一副三角板重叠放在一起,使直角顶点重合于点O.若∠AOC=130°,则∠BOD等于 ( )
A.30° B.40°
C.50° D.60°
4.已知∠α的补角的一半比∠α小30°,则∠α等于 ( )
A.50° B.60° C.70° D.80°
一个角的余角比它的补角的13还少20°,求这个角的度数.
6.如图,已知∠AOD=150°.
(1)如图(a),∠AOC=∠BOD=90°,则∠BOC的余角是 °,∠BOC= °.?
(2)如图(b),已知∠AOB与∠BOC互为余角.
①若OB平分∠AOD,求∠BOC的度数;
②若∠COD是∠BOC的4倍,求∠BOC的度数.
命题点 2 互余与互补的性质
7.如图,∠EDC=∠CDF=90°,∠1=∠2.
(1)图中哪些角互为余角,哪些角互为补角?
(2)∠ADF与∠BDE有什么数量关系?∠ADC与∠BDC有什么数量关系?为什么?
8.如图,已知∠1+∠2=90°.
(1)若∠2+∠3=90°,则∠1与∠3是什么关系?为什么?
(2)若要使∠2与∠4相等,则∠1与∠4要满足什么关系?为什么?
命题点 3 方向角
9.小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西25°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是 ( )
4029710288290A.左转85° B.右转85°
C.右转95° D.左转95°
如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,那么∠AOB的大小为 °.?
368427043815011.如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;?
(2)若射线OE平分∠COD,求∠AOE的度数.
12.如图①,将一副三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,则∠ACB= °;若∠ACB=140°,则∠DCE= °.?
(2)猜想∠ACB与∠DCE有什么特殊的数量关系,并说明理由.
(3)如图②,若将两个同样的含60°角的三角尺的顶点A重合在一起,则∠DAB与∠CAE有何数量关系?请说明理由.
(4)如图③,已知∠AOB=α,∠COD=β(α,β都是锐角),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC之间的数量关系.
13.如果两个角的差的绝对值等于90°,就称这两个角互为反余角,其中一个角叫做另一个角的反余角.例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为反余角,其中∠1是∠2的反余角,∠2也是∠1的反余角.
(1)如图O为直线AB上一点,∠AOC=∠DOE=90°,∠AOE的反余角是 ,∠BOE的反余角是 ;?
(2)若一个角的反余角是它的补角的23,求这个角的度数.
典题讲评与答案详析
1.A [解析] 因为一个角的余角是44°,
所以这个角的度数是90°-44°=46°.
所以这个角的补角是180°-46°=134°.
故选A.
2.D
3.C [解析] 因为∠AOC=130°,
所以∠BOC=∠AOC-∠AOB=40°.
所以∠BOD=∠COD-∠BOC=50°.
故选C.
4.D [解析] 依题意得∠α-12(180°-∠α)=30°,
解得∠α=80°.
故选D.
5.解:设这个角的度数为x,则它的余角为90°-x,补角为180°-x.
根据题意,得90°-x=13(180°-x)-20°,
解得x=75°.
即这个角的度数为75°.
6.解:(1)60 30
[解析] 因为∠AOC=∠BOD=90°,
所以∠BOC+∠AOB=90°,∠BOC+∠COD=90°.
所以∠BOC的余角是∠AOB和∠COD.
因为∠AOD=150°,∠AOC=90°,
所以∠COD=60°.
因为∠BOD=90°,
所以∠BOC=30°.
故答案为60,30.
(2)①因为∠AOB与∠BOC互为余角,
所以∠AOC=∠AOB+∠BOC=90°.
因为OB平分∠AOD,
所以∠AOB=12∠AOD=12×150°=75°.
所以∠BOC=∠AOC-∠AOB=90°-75°=15°.
②由①知∠AOC=90°.
因为∠COD=∠AOD-∠AOC=150°-90°=60°,
且∠COD是∠BOC的4倍,
所以∠BOC=15°.
7.解:(1)因为∠EDC=∠CDF=90°,∠1=∠2,
所以∠1和∠ADC,∠1和∠BDC,∠2和∠ADC,∠2和∠BDC互为余角;
∠1和∠ADF,∠2和∠ADF,∠EDC和∠CDF,∠2和∠BDE,∠1和∠BDE互为补角.
(2)∠ADF=∠BDE,∠ADC=∠BDC.
理由:因为∠1=∠2,∠1+∠ADF=180°,∠2+∠BDE=180°,所以∠ADF=∠BDE.
因为∠EDC=∠CDF=90°,
所以∠1+∠ADC=90°,∠2+∠BDC=90°.
又因为∠1=∠2,
所以∠ADC=∠BDC.
8.解:(1)∠1=∠3.
理由:因为∠1+∠2=90°,∠2+∠3=90°,
所以∠1=∠3.
(2)∠1+∠4=90°.
理由:因为∠1+∠2=90°,∠1+∠4=90°,
所以∠2=∠4.
9.B [解析] 如图:
60°+25°=85°.
由北偏西25°转向北偏东60°,需要向右转85°.
故选B.
10.140 [解析] 因为点A在点O北偏西60°的方向上,
所以OA与表示正西方向的射线的夹角为90°-60°=30°.
又因为点B在点O的南偏东20°的方向上,
所以∠AOB=30°+90°+20°=140°.
故答案为:140.
11.解:(1)如图,因为OB的方向是北偏西40°,OA的方向是北偏东15°,
所以∠FOB=40°,∠FOA=15°.
所以∠AOB=∠FOB+∠FOA=55°.
因为∠AOB=∠AOC,所以∠AOC=55°.
所以∠FOC=∠FOA+∠AOC=70°.
所以OC的方向是北偏东70°.
故答案为北偏东70°.
(2)因为∠AOB=55°,∠AOC=∠AOB=55°,
所以∠BOC=110°.
因为射线OD是OB的反向延长线,
所以∠BOD=180°.
所以∠COD=180°-110°=70°.
因为OE平分∠COD,所以∠COE=35°.
又因为∠AOC=55°,所以∠AOE=90°.
12.解:(1)145 40 [解析] 因为∠ACD=90°,∠DCE=35°,
所以∠ACE=90°-35°=55°.
因为∠BCE=90°,
所以∠ACB=∠ACE+∠BCE=55°+90°=145°.
因为∠ACB=140°,∠BCE=90°,
所以∠ACE=140°-90°=50°.
因为∠ACD=90°,所以∠DCE=90°-50°=40°.
故答案为145,40.
(2)∠ACB+∠DCE=180°.理由如下:
因为∠ACB=∠ACD+∠BCD=90°+∠BCD,
所以∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=90°+90°=180°.
(3)∠DAB+∠CAE=120°.理由如下:
因为∠DAB=∠DAC+∠CAB=60°+∠CAB,
所以∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=60°+60°=120°.
(4)∠AOD+∠BOC=α+β.理由如下:
因为∠AOD=∠COD+∠COA=β+∠COA,
所以∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.
13.解:(1)∠AOD ∠EOC和∠BOD [解析] 因为∠AOD-∠AOE=∠DOE=90°,
所以∠AOE的反余角是∠AOD.
因为∠BOE-∠EOC=∠BOC=180°-∠AOC=90°,∠BOE-∠BOD=∠DOE=90°,
所以∠BOE的反余角为∠EOC和∠BOD.
故答案为∠AOD,∠EOC和∠BOD.
(2)设这个角的度数为x°.
若这个角是锐角,则它的反余角为(90+x)°.
由题意,得90+x=23(180-x),解得x=18.
若这个角是钝角,则它的反余角为(x-90)°.
由题意,得x-90=23(180-x),解得x=126.
综上所述,这个角的度数为18°或126°.
