12.2:全等三角形随堂练习-2021--2022学年人教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 12.2:全等三角形随堂练习-2021--2022学年人教版八年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 184.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 10:55:47 | ||
图片预览


文档简介
1087120010287000 2021人教版八年级上册全等三角形12.2随堂练习
一、 选择题
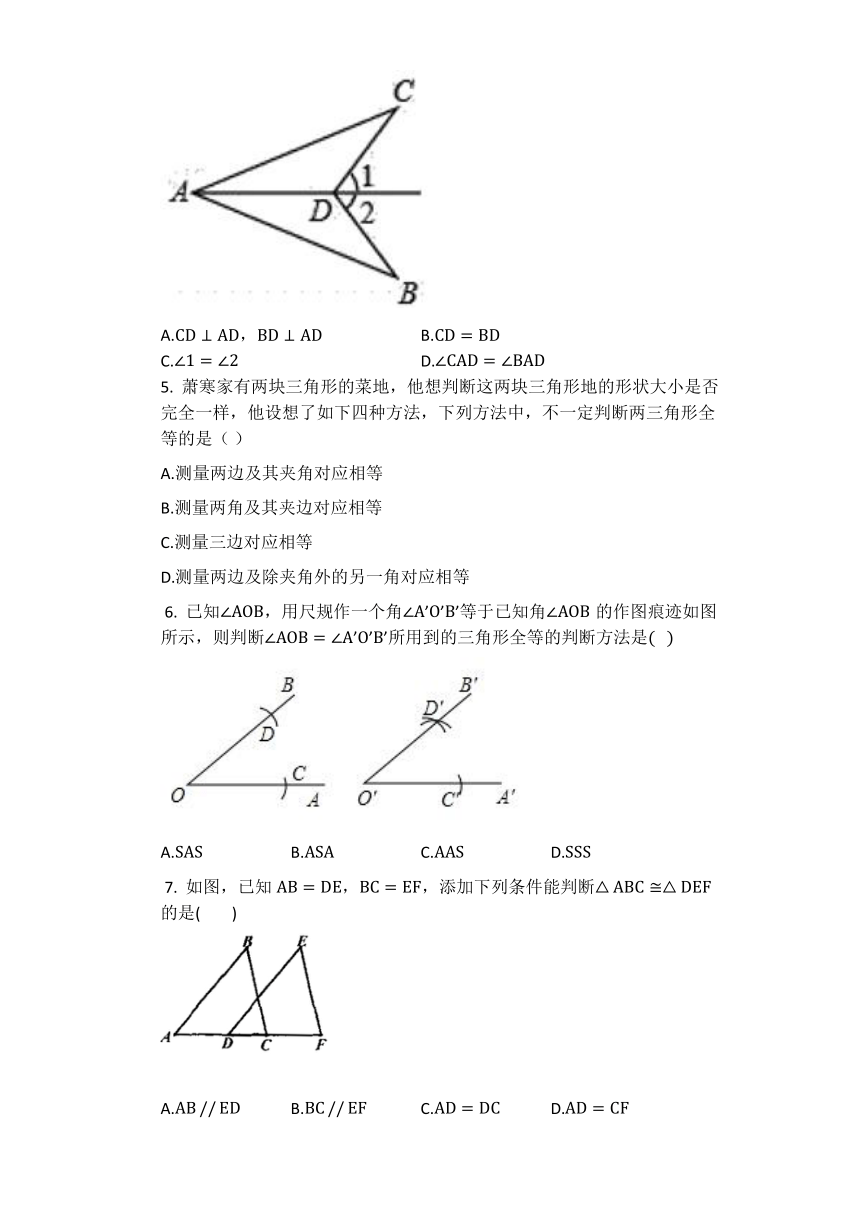
?1. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( )
?
A.AC=DF,BC=EF B.∠A=∠D,AB=DE
C.AC=DF,AB=DE D.∠B=∠E,BC=EF
2. 如图,已知 AC//BD,要使△ABC?△BAD需再补充一个条件,下列条件中,不能选择的是(? ? ? ? )
A.BC//AD B.AC=BD C.BC=AD D.∠C=∠D
?3. 如图,在下列条件中,不能直接证明 △ABD?△ACD的是(????????)
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
4. 如图,要判定△ABD?△ACD,已知AB=AC,若再增加下列条件中的一个,仍不能说明全等,则这个条件是(? ? ? ? )
A.CD⊥AD,BD⊥AD B.CD=BD
C.∠1=∠2 D.∠CAD=∠BAD
5. 萧寒家有两块三角形的菜地,他想判断这两块三角形地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定判断两三角形全等的是( )
A.测量两边及其夹角对应相等
B.测量两角及其夹边对应相等
C.测量三边对应相等
D.测量两边及除夹角外的另一角对应相等
?6. 已知∠AOB,用尺规作一个角∠A’O’B’等于已知角∠AOB的作图痕迹如图所示,则判断∠AOB=∠A’O’B’所用到的三角形全等的判断方法是(???)
A.SAS B.ASA C.AAS D.SSS
?7. 如图,已知AB=DE,BC=EF,添加下列条件能判断△ABC?△DEF的是(? ? ? ? )
A.AB?//?ED B.BC?//?EF C.AD=DC D.AD=CF
?8. 如图所示,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是(? ? ? ? )
A.ASA B.SSS C.SAS D.AAS
?9. 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC?△EFD的是( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠ABC=∠EFD,BC=FD
?10. 如图:已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则有(? ? ? ? ?)
A.△ABD?△AFD B.△AFE?△ADC
C.△AEF?△DFC D.△ABC?△ADE
二、 填空题
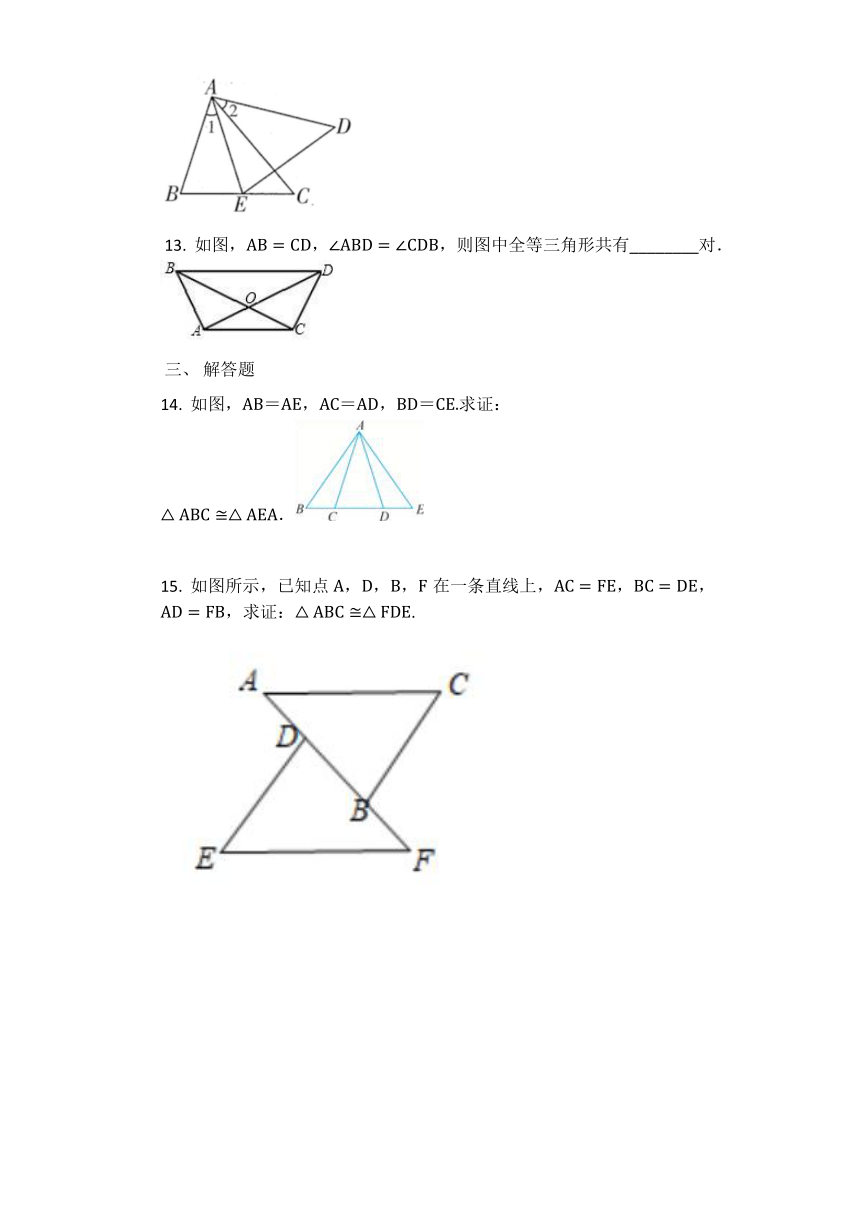
?11. 如图,AD和CB相交于点E,BE=DE,请添加一个条件,使△ABE?△CDE(只添一个即可),你所添加的条件是________.
?12. 如图,AB=AE,AC=AD,要使△ABC?△AED,应添加一个条件是________(填一个即可).
?13. 如图,AB=CD,∠ABD=∠CDB,则图中全等三角形共有________对.
?
三、 解答题 ?
14. 如图,AB=AE,AC=AD,BD=CE.求证:△ABC?△AEA.
?
15. 如图所示,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB,求证:△ABC?△FDE.
?
参考答案与试题解析
一、 选择题
1.
【答案】
C
【解答】
此题暂无解答
2.
【答案】
C
【解答】
解:因为AC//BD,所以∠CAB=∠ABD,
又因为AB=AB,在△ABC和△BAD中,若
①BC//AD,则∠CBA=∠BAD,所以△ABC?△BAD(ASA),故A不符合题意;
②AC=BD,则△ABC?△BAD(SAS),故B不符合题意;
③BC=AD,则无法判定△ABC?△BAD,故C符合题意;
④∠C=∠D,则△ABC?△BAD(AAS),故D不符合题意.
故选C.
3.
【答案】
D
【解答】
解:∵ AD=AD,
A,当BD=DC,AB=AC时,利用SSS证明△ABD?△ACD,故正确;
B,当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD?△ACD,故正确;
C,当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD?△ACD,故正确;
D,当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD?△ACD,故错误.
故选D.
4.
【答案】
C
【解答】
解:A,可用HL判定两个三角形全等,故不符合题意;
B,可用SSS判定两个三角形全等,故不符合题意;
C,∵∠1=∠2,∴∠CDA=∠BDA,结合已知条件不能判定两个三角形全等,故符合题意;
D,可用SAS判定两个三角形全等,故不符合题意.
故选C.
5.
【答案】
D
【解答】
解:A、可根据SAS定理判定两个三角形全等,故此选项不合题意;
B、可根据ASA定理判定两个三角形全等,故此选项不合题意;
C、可根据SSS定理判定两个三角形全等,故此选项不合题意;
D、不能证明两三角形全等,故此选项符合题意,
故选:D.
6.
【答案】
D
【解答】
此题暂无解答
7.
【答案】
D
【解答】
解:A、添加AB?//?ED不能用SSA进行判定,故本选项错误;
B、添加BC?//?EF不能用SSA进行判定,故本选项错误;
C、添加AD=DC不能判定△ABC?△DEF,故本选项错误;
D、添加AD=CF可得出AC=DF,然后可用SSS进行判定,故本选项正确.
故选D.
8.
【答案】
A
【解答】
解:有完整的两角及夹边,符合ASA,
满足题目要求的条件,是符合题意的.
故选A.
9.
【答案】
C
【解答】
此题暂无解答
10.
【答案】
D
【解答】
解:∵ ∠1=∠2=∠3,
∴ ∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE.
∵ ∠E=180??∠2?∠AFE,∠C=180??∠3?∠DFC,
∠DFC=∠AFE(对顶角相等),
∴ ∠E=∠C.
又∵ AC=AE,
∴ △ABC?△ADE.
故选D.
二、 填空题
11.
【答案】
AE=CE(不唯一)
【解答】
此题暂无解答
12.
【答案】
∠1=∠2
【解答】
解:添加条件∠1=∠2.
∵ ∠1=∠2,∠EAC为∠BAC和∠EAD的公共角,
∴ ∠BAC=∠EAD,
在△ABC,△AED中,
∵ AB=AE,∠BAC=∠EAD,AC=AD,
∴ △EAC?△AED(SAS).
故答案为:∠1=∠2.
13.
【答案】
3
【解答】
解:∵ AB=CD,∠ABD=∠CDB,BD=BD
∴ △ABD?△CDB;
∴ ∠ADB=∠CBD,∠BAD=∠DCB
∵ AB=CD,∠BOA=∠DOC
∴ △BOA?△DOC;
∴ OA=OC
∴ ∠OAC=∠OCA
∵ ∠BAO=∠DCO
∴ ∠BAC=∠DCA
∵ AB=CD,AC=AC
∴ △BAC?△DCA.
故答案为:3.
三、 解答题
14.
【答案】
证明:∵BD=CE,
∴BC=DE
又∵AB=AE,AC=AD
∴△ABC?△AEA(SSS)
【解答】
此题暂无解答
15.
【答案】
证明:∵ AD=FB,
∴ AD+DB=FB+DB,
∴ AB=DF.
又∵ AC=FE,BC=DE,
∴ △ABC?△FDE(SSS).
【解答】
证明:∵ AD=FB,
∴ AD+DB=FB+DB,
∴ AB=DF.
又∵ AC=FE,BC=DE,
∴ △ABC?△FDE(SSS).
一、 选择题
?1. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( )
?
A.AC=DF,BC=EF B.∠A=∠D,AB=DE
C.AC=DF,AB=DE D.∠B=∠E,BC=EF
2. 如图,已知 AC//BD,要使△ABC?△BAD需再补充一个条件,下列条件中,不能选择的是(? ? ? ? )
A.BC//AD B.AC=BD C.BC=AD D.∠C=∠D
?3. 如图,在下列条件中,不能直接证明 △ABD?△ACD的是(????????)
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
4. 如图,要判定△ABD?△ACD,已知AB=AC,若再增加下列条件中的一个,仍不能说明全等,则这个条件是(? ? ? ? )
A.CD⊥AD,BD⊥AD B.CD=BD
C.∠1=∠2 D.∠CAD=∠BAD
5. 萧寒家有两块三角形的菜地,他想判断这两块三角形地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定判断两三角形全等的是( )
A.测量两边及其夹角对应相等
B.测量两角及其夹边对应相等
C.测量三边对应相等
D.测量两边及除夹角外的另一角对应相等
?6. 已知∠AOB,用尺规作一个角∠A’O’B’等于已知角∠AOB的作图痕迹如图所示,则判断∠AOB=∠A’O’B’所用到的三角形全等的判断方法是(???)
A.SAS B.ASA C.AAS D.SSS
?7. 如图,已知AB=DE,BC=EF,添加下列条件能判断△ABC?△DEF的是(? ? ? ? )
A.AB?//?ED B.BC?//?EF C.AD=DC D.AD=CF
?8. 如图所示,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是(? ? ? ? )
A.ASA B.SSS C.SAS D.AAS
?9. 如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC?△EFD的是( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠ABC=∠EFD,BC=FD
?10. 如图:已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则有(? ? ? ? ?)
A.△ABD?△AFD B.△AFE?△ADC
C.△AEF?△DFC D.△ABC?△ADE
二、 填空题
?11. 如图,AD和CB相交于点E,BE=DE,请添加一个条件,使△ABE?△CDE(只添一个即可),你所添加的条件是________.
?12. 如图,AB=AE,AC=AD,要使△ABC?△AED,应添加一个条件是________(填一个即可).
?13. 如图,AB=CD,∠ABD=∠CDB,则图中全等三角形共有________对.
?
三、 解答题 ?
14. 如图,AB=AE,AC=AD,BD=CE.求证:△ABC?△AEA.
?
15. 如图所示,已知点A,D,B,F在一条直线上,AC=FE,BC=DE,AD=FB,求证:△ABC?△FDE.
?
参考答案与试题解析
一、 选择题
1.
【答案】
C
【解答】
此题暂无解答
2.
【答案】
C
【解答】
解:因为AC//BD,所以∠CAB=∠ABD,
又因为AB=AB,在△ABC和△BAD中,若
①BC//AD,则∠CBA=∠BAD,所以△ABC?△BAD(ASA),故A不符合题意;
②AC=BD,则△ABC?△BAD(SAS),故B不符合题意;
③BC=AD,则无法判定△ABC?△BAD,故C符合题意;
④∠C=∠D,则△ABC?△BAD(AAS),故D不符合题意.
故选C.
3.
【答案】
D
【解答】
解:∵ AD=AD,
A,当BD=DC,AB=AC时,利用SSS证明△ABD?△ACD,故正确;
B,当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD?△ACD,故正确;
C,当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD?△ACD,故正确;
D,当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD?△ACD,故错误.
故选D.
4.
【答案】
C
【解答】
解:A,可用HL判定两个三角形全等,故不符合题意;
B,可用SSS判定两个三角形全等,故不符合题意;
C,∵∠1=∠2,∴∠CDA=∠BDA,结合已知条件不能判定两个三角形全等,故符合题意;
D,可用SAS判定两个三角形全等,故不符合题意.
故选C.
5.
【答案】
D
【解答】
解:A、可根据SAS定理判定两个三角形全等,故此选项不合题意;
B、可根据ASA定理判定两个三角形全等,故此选项不合题意;
C、可根据SSS定理判定两个三角形全等,故此选项不合题意;
D、不能证明两三角形全等,故此选项符合题意,
故选:D.
6.
【答案】
D
【解答】
此题暂无解答
7.
【答案】
D
【解答】
解:A、添加AB?//?ED不能用SSA进行判定,故本选项错误;
B、添加BC?//?EF不能用SSA进行判定,故本选项错误;
C、添加AD=DC不能判定△ABC?△DEF,故本选项错误;
D、添加AD=CF可得出AC=DF,然后可用SSS进行判定,故本选项正确.
故选D.
8.
【答案】
A
【解答】
解:有完整的两角及夹边,符合ASA,
满足题目要求的条件,是符合题意的.
故选A.
9.
【答案】
C
【解答】
此题暂无解答
10.
【答案】
D
【解答】
解:∵ ∠1=∠2=∠3,
∴ ∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE.
∵ ∠E=180??∠2?∠AFE,∠C=180??∠3?∠DFC,
∠DFC=∠AFE(对顶角相等),
∴ ∠E=∠C.
又∵ AC=AE,
∴ △ABC?△ADE.
故选D.
二、 填空题
11.
【答案】
AE=CE(不唯一)
【解答】
此题暂无解答
12.
【答案】
∠1=∠2
【解答】
解:添加条件∠1=∠2.
∵ ∠1=∠2,∠EAC为∠BAC和∠EAD的公共角,
∴ ∠BAC=∠EAD,
在△ABC,△AED中,
∵ AB=AE,∠BAC=∠EAD,AC=AD,
∴ △EAC?△AED(SAS).
故答案为:∠1=∠2.
13.
【答案】
3
【解答】
解:∵ AB=CD,∠ABD=∠CDB,BD=BD
∴ △ABD?△CDB;
∴ ∠ADB=∠CBD,∠BAD=∠DCB
∵ AB=CD,∠BOA=∠DOC
∴ △BOA?△DOC;
∴ OA=OC
∴ ∠OAC=∠OCA
∵ ∠BAO=∠DCO
∴ ∠BAC=∠DCA
∵ AB=CD,AC=AC
∴ △BAC?△DCA.
故答案为:3.
三、 解答题
14.
【答案】
证明:∵BD=CE,
∴BC=DE
又∵AB=AE,AC=AD
∴△ABC?△AEA(SSS)
【解答】
此题暂无解答
15.
【答案】
证明:∵ AD=FB,
∴ AD+DB=FB+DB,
∴ AB=DF.
又∵ AC=FE,BC=DE,
∴ △ABC?△FDE(SSS).
【解答】
证明:∵ AD=FB,
∴ AD+DB=FB+DB,
∴ AB=DF.
又∵ AC=FE,BC=DE,
∴ △ABC?△FDE(SSS).
