1.2.1矩形的性质 练习题-2021-2022学年九年级数学北师大版上册(Word版 含答案)
文档属性
| 名称 | 1.2.1矩形的性质 练习题-2021-2022学年九年级数学北师大版上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 210.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 15:46:24 | ||
图片预览


文档简介
1.2.1 矩形的性质
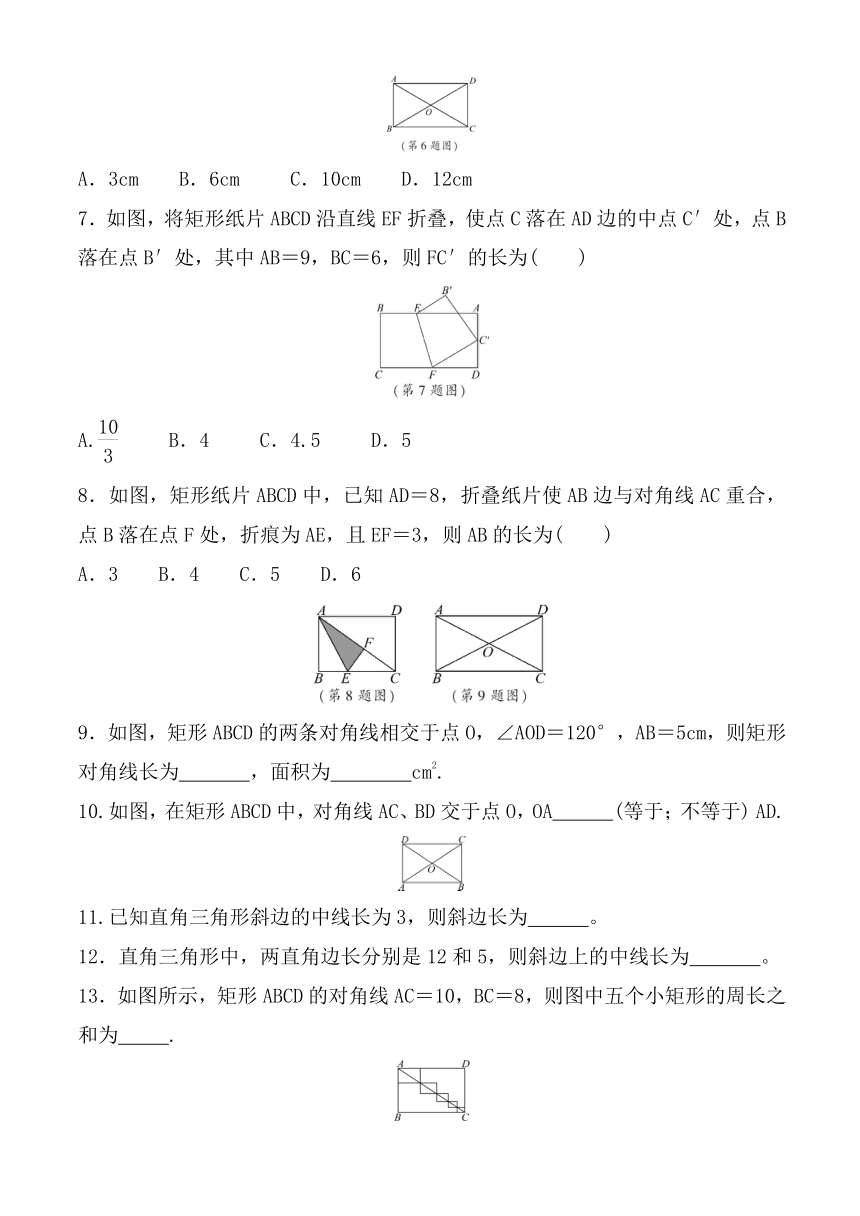
1.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
2.如图,在矩形ABCD中,对角线AC=8cm,∠AOD=120°,则AB的长为( )
A.cm B.2cm C.2cm D.4cm
3.如图,“人字形”屋梁中,AB=AC,点E、F、D分别是AB、AC、BC的中点,若AB=6m,∠B=30°,则支撑“人字形”屋梁的木料DE、AD、DF共有( )
A.5m B.8m C.9m D.10m
4.如图,点O是矩形ABCD的对角线AC的中点,点M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
A.6 B.20 C.21 D.24
5.矩形具有而一般平行四边形不具有的特征是( )
A.对角线相等 B.对边相等 C.对角相等 D.对角线互相平分
6.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
A.3cm B.6cm C.10cm D.12cm
7.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为( )
A. B.4 C.4.5 D.5
8.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
9.如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=5cm,则矩形对角线长为 ,面积为 cm2.
10.如图,在矩形ABCD中,对角线AC、BD交于点O,OA (等于;不等于) AD.
11.已知直角三角形斜边的中线长为3,则斜边长为 。
12.直角三角形中,两直角边长分别是12和5,则斜边上的中线长为 。
13.如图所示,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为 .
14.如图,在矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F,求证:BE=CF.
15.如图,AD、BE是△ABC的高,F是DE的中点,G是AB的中点.
求证:GF⊥DE.
16.矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
求证:(1)四边形AFCE是平行四边形;
(2)EG=FH.
17.如图,在矩形ABCD中,E是AD上的一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
答案;
1-8 CDCBA ADD
9. 10cm 25
10. 等于
11. 6
12. .6.5
13. 28
14. 证明:∵四边形ABCD是矩形,∴OB=OC,∵BE⊥AC,CF⊥BD,∴∠OEB=∠OFC=90°,∵∠EOB=∠FOC,∴△BOE≌△COF,∴BE=CF.
15. 证明:连接GE、GD,∵AD、BE是△ABC的高,G是AB的中点,∴GE=AB,GD=AB,∴GE=GD,∵F为DE的中点,∴GF⊥DE.
16. (1)证明:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵E、F分别是AD、BC的中点,∴AE=AD,CF=BC,∴AE=CF,∴四边形AFCE是平行四边形;
(2)证明:∵四边形AFCE是平行四边形,∴CE∥AF,∴∠DGE=∠AHD=∠BHF,∵AD∥BC,∴∠EDG=∠FBH,在△DEG和△BFH中∴△DEG≌△BFH(AAS),∴EG=FH.
17. (1)证明:∵PQ垂直平分BE,∴QB=QE,OB=OE,∵四边形ABCD是矩形,∴AD∥BC,∴∠PEO=∠QBO,在△BOQ与△EOP中,,∴△BOQ≌△EOP(ASA),∴PE=QB,又∵AD∥BC,∴四边形BPEQ是平行四边形,又∵QB=QE,∴四边形BPEQ是菱形;
(2)解:∵O、F分别为PQ,AB的中点,∴AE+BE=2OF+2OB=18,设AE=x,则BE=18-x,在Rt△ABE中,62+x2=(18-x)2,解得x=8,BE=18-x=10,∴OB=BE=5.设PE=y,则AP=8-y,BP=PE=y,在Rt△ABP中,62+(8-y)2=y2,解得y=,在Rt△BOP中,PO==,∴PQ=2PO=.
1.如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
2.如图,在矩形ABCD中,对角线AC=8cm,∠AOD=120°,则AB的长为( )
A.cm B.2cm C.2cm D.4cm
3.如图,“人字形”屋梁中,AB=AC,点E、F、D分别是AB、AC、BC的中点,若AB=6m,∠B=30°,则支撑“人字形”屋梁的木料DE、AD、DF共有( )
A.5m B.8m C.9m D.10m
4.如图,点O是矩形ABCD的对角线AC的中点,点M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
A.6 B.20 C.21 D.24
5.矩形具有而一般平行四边形不具有的特征是( )
A.对角线相等 B.对边相等 C.对角相等 D.对角线互相平分
6.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
A.3cm B.6cm C.10cm D.12cm
7.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为( )
A. B.4 C.4.5 D.5
8.如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
9.如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=5cm,则矩形对角线长为 ,面积为 cm2.
10.如图,在矩形ABCD中,对角线AC、BD交于点O,OA (等于;不等于) AD.
11.已知直角三角形斜边的中线长为3,则斜边长为 。
12.直角三角形中,两直角边长分别是12和5,则斜边上的中线长为 。
13.如图所示,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为 .
14.如图,在矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F,求证:BE=CF.
15.如图,AD、BE是△ABC的高,F是DE的中点,G是AB的中点.
求证:GF⊥DE.
16.矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
求证:(1)四边形AFCE是平行四边形;
(2)EG=FH.
17.如图,在矩形ABCD中,E是AD上的一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
答案;
1-8 CDCBA ADD
9. 10cm 25
10. 等于
11. 6
12. .6.5
13. 28
14. 证明:∵四边形ABCD是矩形,∴OB=OC,∵BE⊥AC,CF⊥BD,∴∠OEB=∠OFC=90°,∵∠EOB=∠FOC,∴△BOE≌△COF,∴BE=CF.
15. 证明:连接GE、GD,∵AD、BE是△ABC的高,G是AB的中点,∴GE=AB,GD=AB,∴GE=GD,∵F为DE的中点,∴GF⊥DE.
16. (1)证明:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵E、F分别是AD、BC的中点,∴AE=AD,CF=BC,∴AE=CF,∴四边形AFCE是平行四边形;
(2)证明:∵四边形AFCE是平行四边形,∴CE∥AF,∴∠DGE=∠AHD=∠BHF,∵AD∥BC,∴∠EDG=∠FBH,在△DEG和△BFH中∴△DEG≌△BFH(AAS),∴EG=FH.
17. (1)证明:∵PQ垂直平分BE,∴QB=QE,OB=OE,∵四边形ABCD是矩形,∴AD∥BC,∴∠PEO=∠QBO,在△BOQ与△EOP中,,∴△BOQ≌△EOP(ASA),∴PE=QB,又∵AD∥BC,∴四边形BPEQ是平行四边形,又∵QB=QE,∴四边形BPEQ是菱形;
(2)解:∵O、F分别为PQ,AB的中点,∴AE+BE=2OF+2OB=18,设AE=x,则BE=18-x,在Rt△ABE中,62+x2=(18-x)2,解得x=8,BE=18-x=10,∴OB=BE=5.设PE=y,则AP=8-y,BP=PE=y,在Rt△ABP中,62+(8-y)2=y2,解得y=,在Rt△BOP中,PO==,∴PQ=2PO=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
