1.2.1 任意角的三角函数 课件-2020-2021学年高中数学必修四(20张PPT)
文档属性
| 名称 | 1.2.1 任意角的三角函数 课件-2020-2021学年高中数学必修四(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 09:42:20 | ||
图片预览


文档简介
(共20张PPT)
情境导入
寓意:日出日落、潮涨潮落、草枯草绿,
东升西落照苍穹
自然界中存在许多“按照一定规律周而复始
影短影长角不同的现象,我们把他称为周期现象,三角函
数是描述周期现象的重要数学模型。
昼夜循环潮起伏
冬春更替草枯荣
李尚志
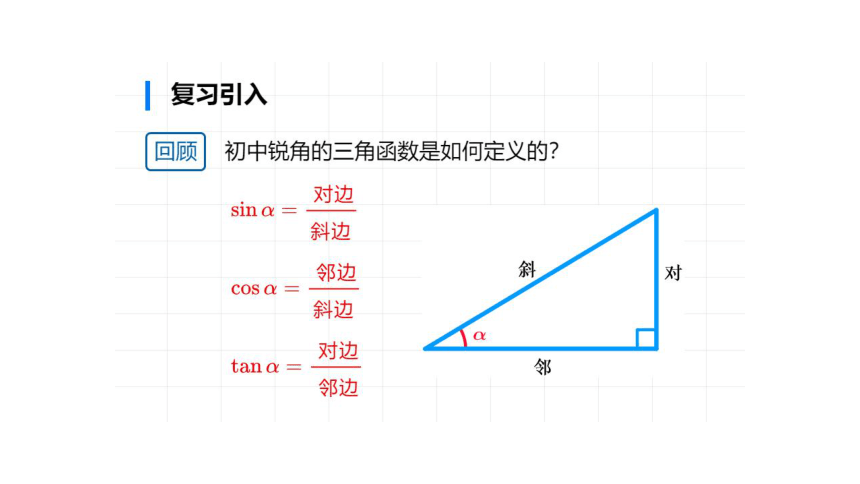
复习引入
回顾初中锐角的三角函数是如何定义的?
对边
斜边
邻边
COS
O
斜边
对边
tan
邻边
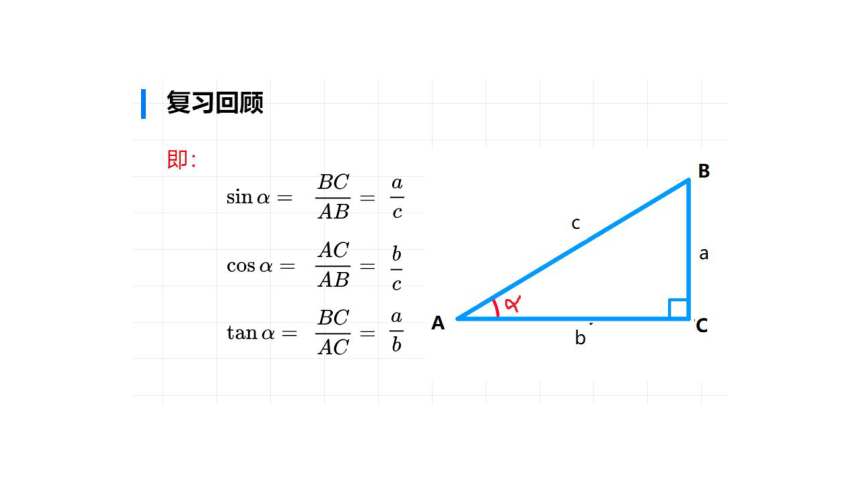
复习回顾
BC
AB
acbc
C
Ac
COS
O
AB
BC
tan
a
aA
Ac
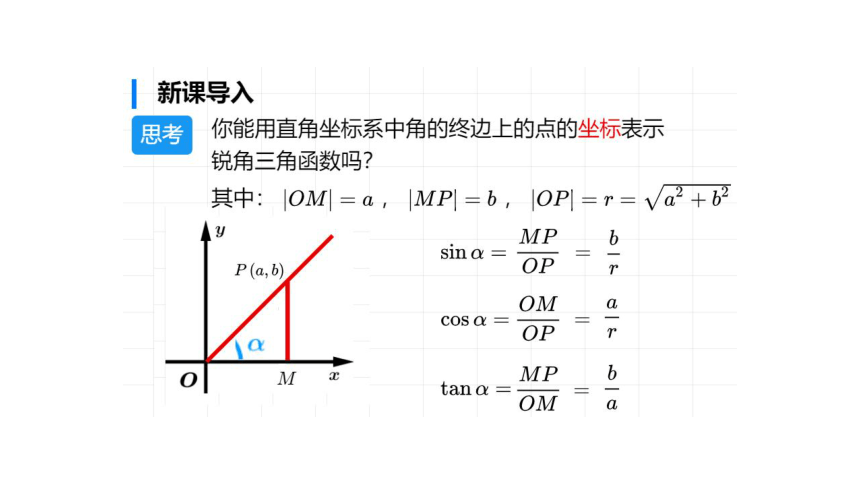
新课导入
思考你能用直角坐标系中角的终边上的点的坐标表示
锐角三角函数吗?
其中:OM|=a,|MP=b,OP|=r=√a2+b2
MP
SIn
a
P
OP
oM
COS
O
OP
O
MP
tan
a
OM
ba
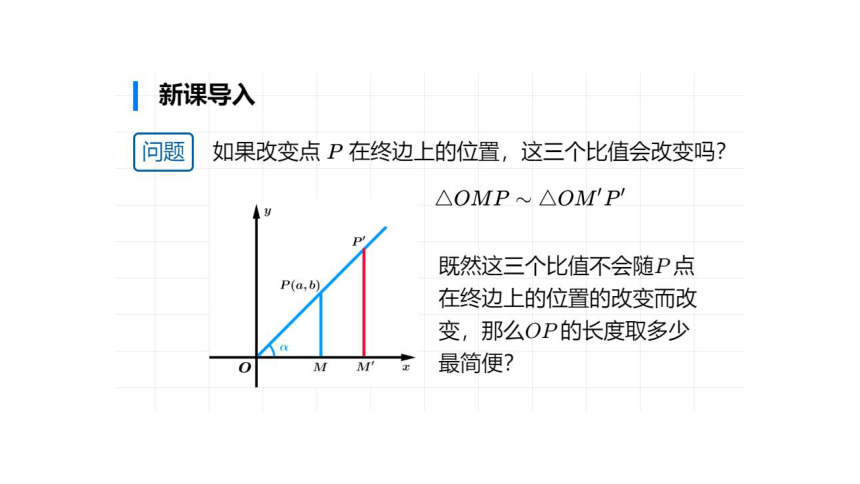
新课导入
题如果改变点P在终边上的位置,这三个比值会改变吗?
△OMP~△OMP
既然这三个比值不会随P点
P(a,
b)
在终边上的位置的改变而改
变,那么OP的长度取多少
MM最简便?
新课导入
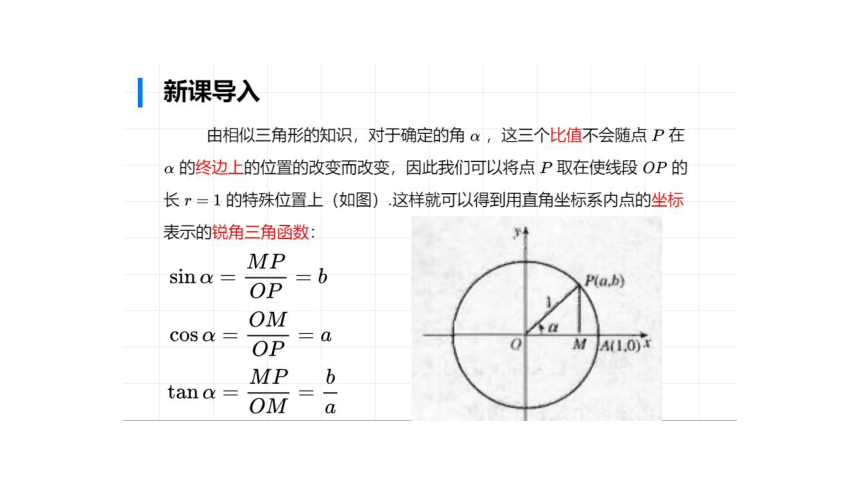
由相似三角形的知识,对于确定的角α,这三个比值不会随点P在
a的终边上的位置的改变而改变,因此我们可以将点P取在使线段OP的
长r=1的特殊位置上(如图)这样就可以得到用直角坐标系内点的坐标
表示的锐角三角函数
MP
SIn
a
OP
Pa,b)
OM
COS
a
OP
M
JA(.O)-
MP
b
tan
OM
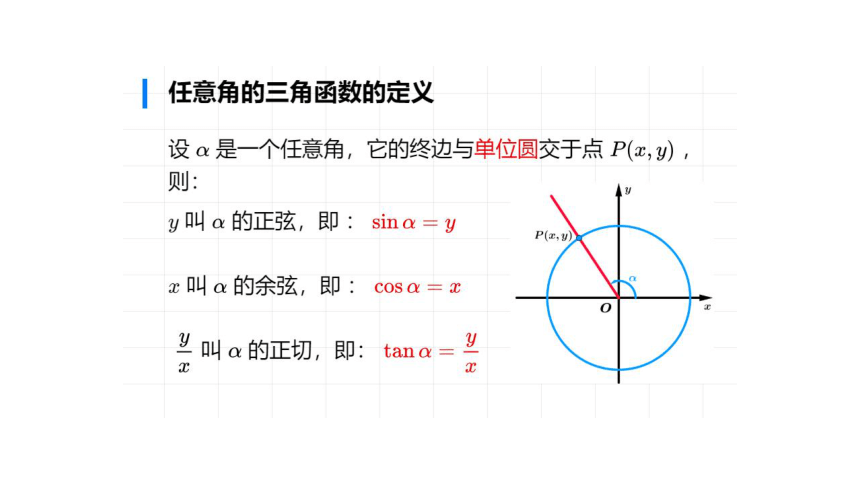
任意角的三角函数的定义
设a是一个任意角,它的终边与单位圆交于点P(x,y)
则:
y叫a的正弦,即:sina=y
x叫a的余弦,即:cosa=
y叫a的正切,即:tana
任意角的三角函数的定义
可以看出,对应关系sina=y,cosa=x,
tan
a
(x≠0)都是以角为自变量,以单位圆上的
点的坐标或坐标的比值为函数值的函数,分别称为
弦函数、余弦函数和正切函数,并统称为三角函数
由于角的集合与实数集之间可以建立一一对应关系
角函数可以看成是自变量为实数的函数
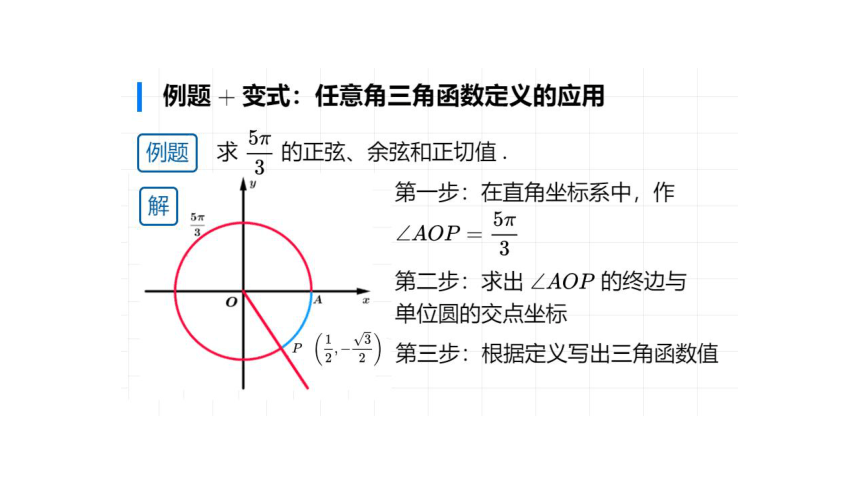
例题+变式:任意角三角函数定义的应用
5丌
例题|求一的正弦、余弦和正切值
解
第一步:在直角坐标系中,作
5丌
∠AOP
第二步:求出∠AOP的终边与
单位圆的交点坐标
第三步:根据定义写出三角函数值
例题+变式:任意角三角函数定义的应用
变式求的正弦、余弦和正切值
解
例题+变式:任意角三角函数定义的应用
例题已知角a的终边经过点P(-3,-4),求角a的
弦、余弦和正切值
y
Mo
M
情境导入
寓意:日出日落、潮涨潮落、草枯草绿,
东升西落照苍穹
自然界中存在许多“按照一定规律周而复始
影短影长角不同的现象,我们把他称为周期现象,三角函
数是描述周期现象的重要数学模型。
昼夜循环潮起伏
冬春更替草枯荣
李尚志
复习引入
回顾初中锐角的三角函数是如何定义的?
对边
斜边
邻边
COS
O
斜边
对边
tan
邻边
复习回顾
BC
AB
acbc
C
Ac
COS
O
AB
BC
tan
a
aA
Ac
新课导入
思考你能用直角坐标系中角的终边上的点的坐标表示
锐角三角函数吗?
其中:OM|=a,|MP=b,OP|=r=√a2+b2
MP
SIn
a
P
OP
oM
COS
O
OP
O
MP
tan
a
OM
ba
新课导入
题如果改变点P在终边上的位置,这三个比值会改变吗?
△OMP~△OMP
既然这三个比值不会随P点
P(a,
b)
在终边上的位置的改变而改
变,那么OP的长度取多少
MM最简便?
新课导入
由相似三角形的知识,对于确定的角α,这三个比值不会随点P在
a的终边上的位置的改变而改变,因此我们可以将点P取在使线段OP的
长r=1的特殊位置上(如图)这样就可以得到用直角坐标系内点的坐标
表示的锐角三角函数
MP
SIn
a
OP
Pa,b)
OM
COS
a
OP
M
JA(.O)-
MP
b
tan
OM
任意角的三角函数的定义
设a是一个任意角,它的终边与单位圆交于点P(x,y)
则:
y叫a的正弦,即:sina=y
x叫a的余弦,即:cosa=
y叫a的正切,即:tana
任意角的三角函数的定义
可以看出,对应关系sina=y,cosa=x,
tan
a
(x≠0)都是以角为自变量,以单位圆上的
点的坐标或坐标的比值为函数值的函数,分别称为
弦函数、余弦函数和正切函数,并统称为三角函数
由于角的集合与实数集之间可以建立一一对应关系
角函数可以看成是自变量为实数的函数
例题+变式:任意角三角函数定义的应用
5丌
例题|求一的正弦、余弦和正切值
解
第一步:在直角坐标系中,作
5丌
∠AOP
第二步:求出∠AOP的终边与
单位圆的交点坐标
第三步:根据定义写出三角函数值
例题+变式:任意角三角函数定义的应用
变式求的正弦、余弦和正切值
解
例题+变式:任意角三角函数定义的应用
例题已知角a的终边经过点P(-3,-4),求角a的
弦、余弦和正切值
y
Mo
M
