1.1.1 探索勾股定理

1.1.1探索勾股定理
姓名：
一、回顾，操作，猜想
在学“HL”时我们知道，一个直角三角形有两条边确定的话，那么第三条边也会确定，说明直角三角形的三边关系会更加特殊，请按以下要求小组内操作，讨论猜想：
（1）画一直角三角形1，使得直角边a为3，直角边b为 4，看斜边c多少
（2）画一直角三角形，使得直角边a 为5，斜边c为13，看另一直角边b多少
（3）将（1）（2）中的数据填入表格，并猜想直角三角形的三边满足什么关系呢
直角边a 直角边b 斜边c 三边关系满足关系
直角三角形1
直角边a 直角边b 斜边c 三边关系满足关系
直角三角形2
（4）任画一直角三角形，量出三边长度，看得到的数据是否满足你们猜想的关系.
二、导学
（1）勾股定理：
如果直角三角形的两直角边为a，b，斜边为c，那么
（2）数学表达：∵△ABC是直角三角形， ∴
或 者：∵△ABC是直角三角形， ∴
三、提出问题
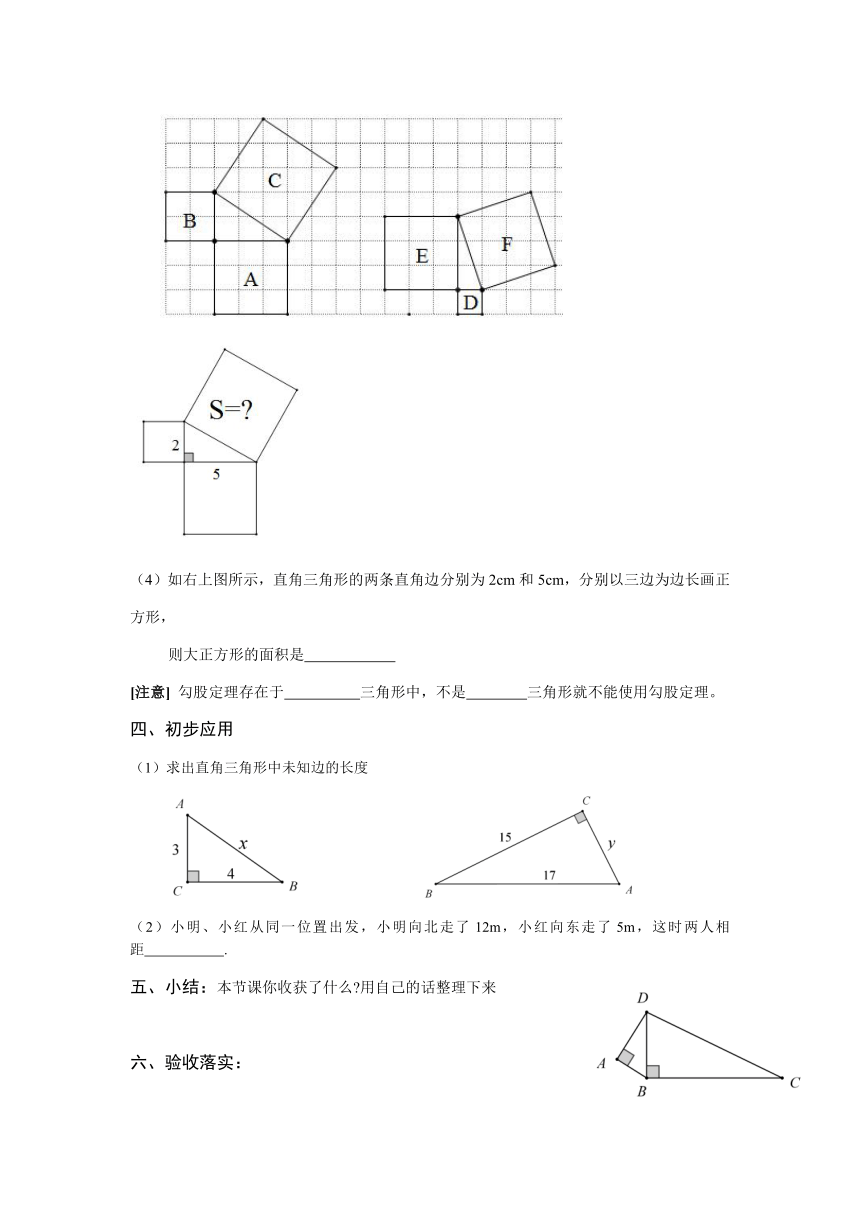
（1）求出以下两幅图中每个正方形的面积吗
（2）你能发现每幅图中三个正方形面积之间的关系吗
（3）以上关系跟中间的直角三角形又有什么关系呢
（4）如右上图所示，直角三角形的两条直角边分别为2cm和5cm，分别以三边为边长画正方形，
则大正方形的面积是
[注意] 勾股定理存在于 三角形中，不是 三角形就不能使用勾股定理。
四、初步应用
（1）求出直角三角形中未知边的长度
（2）小明、小红从同一位置出发，小明向北走了12m，小红向东走了5m，这时两人相距 .
五、小结：本节课你收获了什么 用自己的话整理下来
六、验收落实：
1、已知在Rt△ABC中，∠C=90°。
① 若a=6，c=10，则b=________； ② 若a=7，b=24，则c=________；
2、已知一个直角三角形的斜边长为17cm，一条直角边长为8cm，则它的面积为________；
3、如右上图，∠A =，∠DBC =，AD = 3，AB = 4，BC = 12，则CD=________；（尝试详写）
4、如右图，等腰三角形腰长为5cm，底边长为6cm，求面积.
答 案
四、初步应用
（1）求出直角三角形中未知边的长度
（2）13米
六、验收落实：
1、已知在Rt△ABC中，∠C=90°。
① 若a=6，c=10，则b=________； 8
② 若a=7，b=24，则c=________； 25
2、已知一个直角三角形的斜边长为17cm，一条直角边长为8cm，
则它的面积为________；
3、如右上图，∠A =，∠DBC =，AD = 3，AB = 4，BC = 12，则CD=________；（尝试详写）
解：在Rt△ABD中，，
∴ ∴
在Rt△BCD中，，
∴ ∴
∴
4、如右图，等腰三角形腰长为5cm，底边长为6cm，求面积.
解：过C点作CD⊥AB，∵CA=CB ∴ AD=DB=AB=3
∴在Rt△AC中，，
∴ ∴
∴cm
∴