天津一中2012届高三5月月考 文科数学试题
文档属性
| 名称 | 天津一中2012届高三5月月考 文科数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 156.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-28 00:00:00 | ||
图片预览





文档简介
天津一中2011—2012学年高三五月考
数学试卷(文科)
一、选择题:
1、设a,b为实数,若复数,则( )
A. B. C. D.
2、设变量满足约束条件则目标函数的最大值为( )
A.10 B.12 C.13 D.14
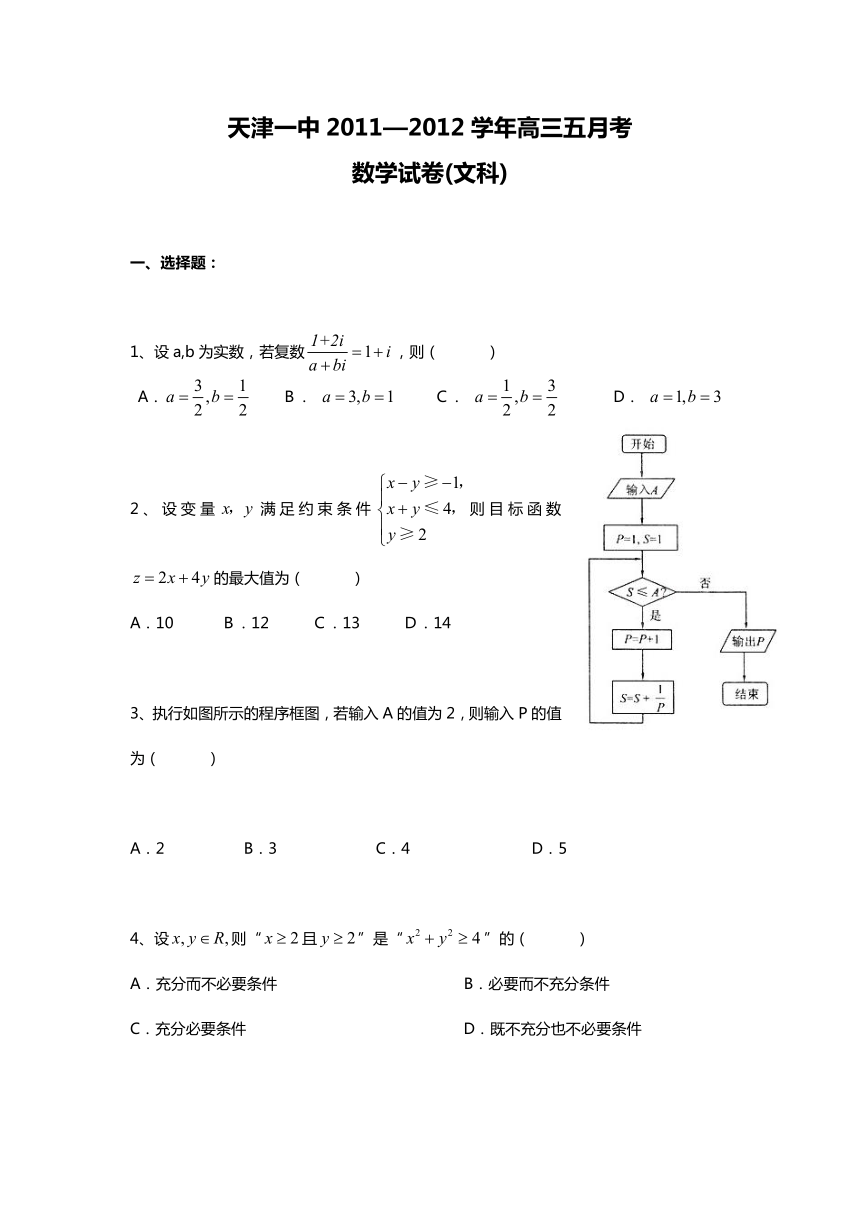
3、执行如图所示的程序框图,若输入A的值为2,则输入P的值为( )
A.2 B.3 C.4 D.5
4、设则“且”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5、设,则( )
A. B. C. D.
6、已知抛物线,过其焦点且斜率为1的直线交抛物线与、两点,若线段的中点的纵坐标为2,则该抛物线的准线方程为( )
A. B. C. D.
7、已知数列对任意的满足,且,那么等于( )
A. B. C. D.
8、定义一种运算,令,则函数的最大值是( )
A. B.1 C. D.
二、填空题:
9、已知集合,且,则 。
10、一个几何体的三视图及部分数据如右图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于 。
11、直线截圆所得的劣弧所对的圆心角为 。
12、某公司一年购买某种货物400吨,每次都购买吨,运费为4万元/次,一年的总存储费用为万元,要使一年的总运费与总存储费用之和最小,
则 吨。
13、如图,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=,∠OAP=30°,则CP= 。
14、ABC的外接圆的半径是1,圆心为O,且,,则 。
三、解答题:
15、设函数f(x)=cos(2x+)+sinx
(Ⅰ)求函数f(x)的最大值和最小正周期;
(Ⅱ)设A,B,C为ABC的三个内角,若cosB=,,且C为锐角,求sinA。
16、为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从三个区中抽取个工厂进行调查。已知区中分别有个工厂。
(Ⅰ)求从区中应分别抽取的工厂个数;
(Ⅱ)若从抽得的个工厂中随机地抽取个进行调查结果的对比,用列举法计算这个工厂中至少有个来自区的概率。
17、已知矩形ABCD所在平面外一点P,平面ABCD,E、F分别是AB、PC的中点
(Ⅰ)求证:;
(Ⅱ)求证:;
(Ⅲ)当PA=AB=AD时,求二面角F-AB-C的度数。
18、已知椭圆的中心在原点,焦点在轴上,椭圆上的点到焦点的最小距离为,离心率为
(Ⅰ)求椭圆的方程;
(Ⅱ)过点(1,0)作直线交椭圆于P、Q两点,试问:在x轴上是否存在一个定点M, 使为定值?若存在,求出这个点M的坐标;若不存在,说明理由。
19、已知函数在上为增函数,且,.
(Ⅰ)求的值;
(Ⅱ)若在上为单调函数,求的取值范围;
(Ⅲ)设,若在上至少存在一个,使得成立,求的取值范围.
20、已知数列的前n项和(n为正整数).
(Ⅰ)令,求证数列是等差数列;
(Ⅱ)求数列的通项公式;
(Ⅲ)令,, 求证:。
参考答案
一.
1—5 ACCAC 6—8 BCA
二.
9.-2
10.
11.60o
12.20
13.
14.3
三.
15.解:
(1)
(2)
16.解:
(1)
应分别从A、B、C区中分别抽取工厂个数
分别为2;3;2
(2)不妨假设7个工厂分别为A1A2;B1B2B3;C1C2;
则7个中任取2个所有可能基本事件共21种
分别包括(A1A2)(A1B1)(A1B2)(A1B3)(A1C1)(A1C2)
(A2B1)(A2B2)(A2B3)(A2C1)(A2C2)(B1B2)
(B1B3)(B1C1)(B1C2)(B2C1)(B2C2)(B3C1)
(B3C2)(C1C2)(B2B3)
其中至少有1个来自A区所有基本事件共有11种
∴7个中至少1个来自A区的概率为
17.解:
(1)
取PD中点M,分别连接FM和AM
∵E,M,F分别为AB,PD和PC中点
(2)
(3)
连结AC,取AC中点O
∵F,O分别为PC,AC中点
∴
18.解:
(1)
(2)不妨假设存在这样定点m(x0,0)使得为定值
一方面,当直线斜率不存在,即x轴时
不为定值不合题意
另一方面:当斜率存在
即x轴
19.解:
(1)
(2)
(3)
20.解:
连结EO,FE
知AB⊥平面EFO
∴∠FEO即为二面角F-AB-C平面角
在Rt△FOE中
(1)
(2)
(3)
数学试卷(文科)
一、选择题:
1、设a,b为实数,若复数,则( )
A. B. C. D.
2、设变量满足约束条件则目标函数的最大值为( )
A.10 B.12 C.13 D.14
3、执行如图所示的程序框图,若输入A的值为2,则输入P的值为( )
A.2 B.3 C.4 D.5
4、设则“且”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5、设,则( )
A. B. C. D.
6、已知抛物线,过其焦点且斜率为1的直线交抛物线与、两点,若线段的中点的纵坐标为2,则该抛物线的准线方程为( )
A. B. C. D.
7、已知数列对任意的满足,且,那么等于( )
A. B. C. D.
8、定义一种运算,令,则函数的最大值是( )
A. B.1 C. D.
二、填空题:
9、已知集合,且,则 。
10、一个几何体的三视图及部分数据如右图所示,侧视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于 。
11、直线截圆所得的劣弧所对的圆心角为 。
12、某公司一年购买某种货物400吨,每次都购买吨,运费为4万元/次,一年的总存储费用为万元,要使一年的总运费与总存储费用之和最小,
则 吨。
13、如图,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=,∠OAP=30°,则CP= 。
14、ABC的外接圆的半径是1,圆心为O,且,,则 。
三、解答题:
15、设函数f(x)=cos(2x+)+sinx
(Ⅰ)求函数f(x)的最大值和最小正周期;
(Ⅱ)设A,B,C为ABC的三个内角,若cosB=,,且C为锐角,求sinA。
16、为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从三个区中抽取个工厂进行调查。已知区中分别有个工厂。
(Ⅰ)求从区中应分别抽取的工厂个数;
(Ⅱ)若从抽得的个工厂中随机地抽取个进行调查结果的对比,用列举法计算这个工厂中至少有个来自区的概率。
17、已知矩形ABCD所在平面外一点P,平面ABCD,E、F分别是AB、PC的中点
(Ⅰ)求证:;
(Ⅱ)求证:;
(Ⅲ)当PA=AB=AD时,求二面角F-AB-C的度数。
18、已知椭圆的中心在原点,焦点在轴上,椭圆上的点到焦点的最小距离为,离心率为
(Ⅰ)求椭圆的方程;
(Ⅱ)过点(1,0)作直线交椭圆于P、Q两点,试问:在x轴上是否存在一个定点M, 使为定值?若存在,求出这个点M的坐标;若不存在,说明理由。
19、已知函数在上为增函数,且,.
(Ⅰ)求的值;
(Ⅱ)若在上为单调函数,求的取值范围;
(Ⅲ)设,若在上至少存在一个,使得成立,求的取值范围.
20、已知数列的前n项和(n为正整数).
(Ⅰ)令,求证数列是等差数列;
(Ⅱ)求数列的通项公式;
(Ⅲ)令,, 求证:。
参考答案
一.
1—5 ACCAC 6—8 BCA
二.
9.-2
10.
11.60o
12.20
13.
14.3
三.
15.解:
(1)
(2)
16.解:
(1)
应分别从A、B、C区中分别抽取工厂个数
分别为2;3;2
(2)不妨假设7个工厂分别为A1A2;B1B2B3;C1C2;
则7个中任取2个所有可能基本事件共21种
分别包括(A1A2)(A1B1)(A1B2)(A1B3)(A1C1)(A1C2)
(A2B1)(A2B2)(A2B3)(A2C1)(A2C2)(B1B2)
(B1B3)(B1C1)(B1C2)(B2C1)(B2C2)(B3C1)
(B3C2)(C1C2)(B2B3)
其中至少有1个来自A区所有基本事件共有11种
∴7个中至少1个来自A区的概率为
17.解:
(1)
取PD中点M,分别连接FM和AM
∵E,M,F分别为AB,PD和PC中点
(2)
(3)
连结AC,取AC中点O
∵F,O分别为PC,AC中点
∴
18.解:
(1)
(2)不妨假设存在这样定点m(x0,0)使得为定值
一方面,当直线斜率不存在,即x轴时
不为定值不合题意
另一方面:当斜率存在
即x轴
19.解:
(1)
(2)
(3)
20.解:
连结EO,FE
知AB⊥平面EFO
∴∠FEO即为二面角F-AB-C平面角
在Rt△FOE中
(1)
(2)
(3)
同课章节目录
