河北省唐山市滦南县2020-2021学年八年级上学期期末数学试卷(word版含答案)
文档属性
| 名称 | 河北省唐山市滦南县2020-2021学年八年级上学期期末数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 08:47:38 | ||
图片预览




文档简介
2020-2021学年河北省唐山市滦南县八年级(上)期末数学试卷
一、选择题(本大题含16个小题;每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列式子中,是分式的是( )
A.
B.
C.﹣
D.
2.已知△ABC≌△DEF,∠A=30°,∠F=85°,则∠B的度数是( )
A.30°
B.85°
C.65°
D.55°
3.下列计算正确的是( )
A.=±7
B.=﹣7
C.=1
D.=
4.在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )
A.
B.
C.
D.
5.若分式的值为0,则x的值为( )
A.±1
B.﹣1
C.1
D.±2
6.如图,已知AC=DB,下列四个条件:①∠A=∠D;②∠ABD=∠DCA;③∠ACB=∠DBC;④∠ABC=∠DCB.其中能使△ABC≌△DCB的有( )
A.1个
B.2个
C.3个
D.4个
7.下列二次根式中,能与合并的是( )
A.
B.
C.
D.
8.如图,在△ABC中.∠C=90°,∠CAB=60°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB,AC于点E、F;②分别以点E、F为圆心,大于EF长为半径画弧,两弧交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )
A.40°
B.50°
C.60°
D.70°
9.把分式(a,b,c均为正)中的b、c的值都扩大为原来的3倍,则分式的值( )
A.不变
B.变为原来的3倍
C.变为原来的
D.变为原来的
10.如图,在△ABC中,BC=10cm,AB的垂直平分线交AB于点D,交边AC于点E,若△BCE的周长等于22cm,则AC的长度等于( )
A.10cm
B.12cm
C.22cm
D.32cm
11.下列计算正确的是( )
A.÷=
B.﹣=
C.+=
D.×=
12.如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是( )
A.12cm
B.16cm
C.18cm
D.20cm
13.数轴上表示下列各数的点,能落在A、B两个点之间的是( )
A.﹣
B.
C.
D.
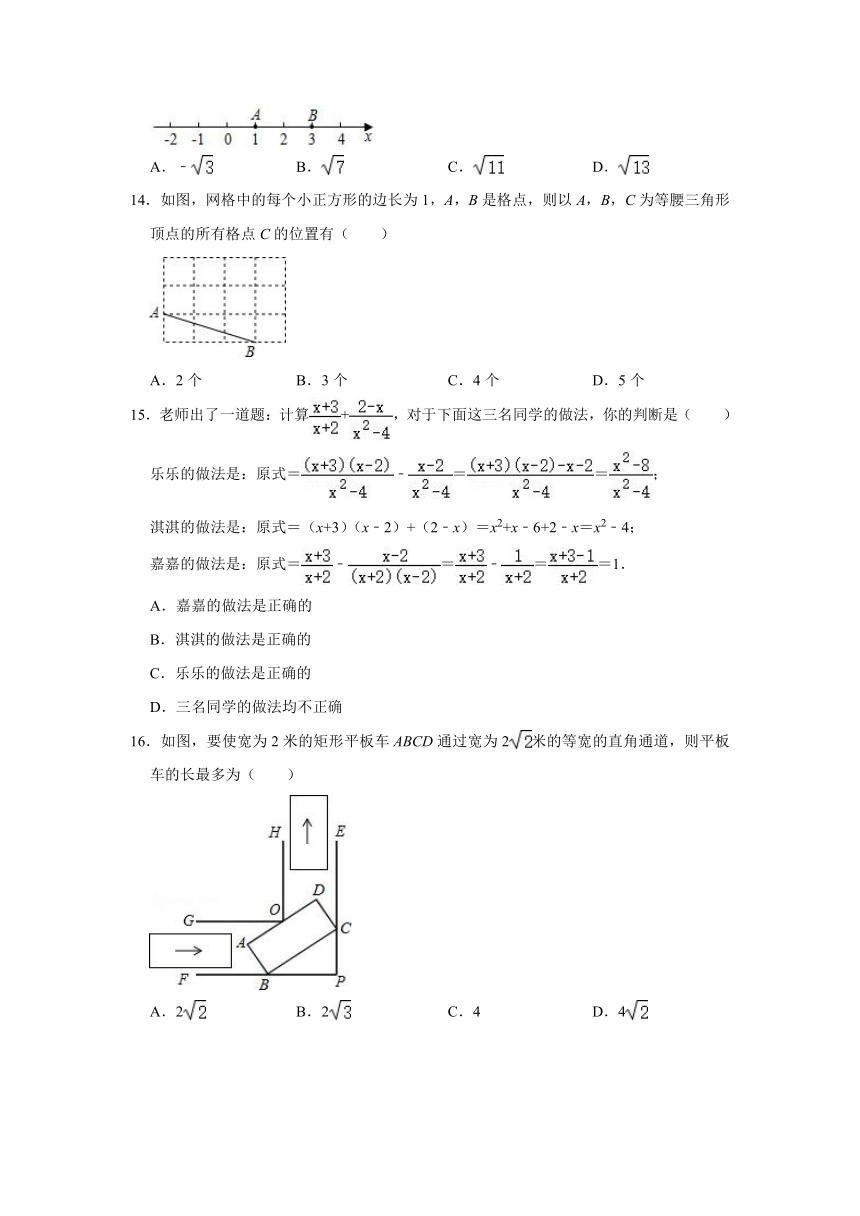
14.如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
A.2个
B.3个
C.4个
D.5个
15.老师出了一道题:计算+,对于下面这三名同学的做法,你的判断是( )
乐乐的做法是:原式=﹣==;
淇淇的做法是:原式=(x+3)(x﹣2)+(2﹣x)=x2+x﹣6+2﹣x=x2﹣4;
嘉嘉的做法是:原式=﹣=﹣==1.
A.嘉嘉的做法是正确的
B.淇淇的做法是正确的
C.乐乐的做法是正确的
D.三名同学的做法均不正确
16.如图,要使宽为2米的矩形平板车ABCD通过宽为2米的等宽的直角通道,则平板车的长最多为( )
A.2
B.2
C.4
D.4
二、填空题(本大题含3个小题:17、18小题每题3分,19小题每空2分,共10分)
17.已知,.则代数式x2+y2﹣2xy的值为
.
18.关于x的方程﹣=2有增根,则m的值为
.
19如图,长方体盒子的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着盒子的表面从点A到点B.
(1)蚂蚁爬行的最短距离是 cm;
(2)若从C处想盒子里面插入一根吸管,要使吸管不落入盒子中,吸管应不少于 cm.
三、解答题(本大题含7小题,共计58分,解答题要求写出必要的解题过程)
20已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
21阅读下列文字,回答问题.
题目:在Rt△ABC中,∠C=90°,若∠A≠45°,所以AC≠BC.
证明:假设AC=BC,因为∠A≠45°,∠C=90°,所以∠A≠∠B.
所以AC≠BC,这与假设矛盾,所以AC≠BC.
上面的证明有没有错误?若没有错误,指出其证明的方法;若有错误,请予以纠正.
22先化简(﹣)÷,然后从0,1,2中选取一个合适的x值代入求值.
23求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半.
(1)在图中按照下面“已知”的要求,画出符合题意的图形,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.
已知:在△ABC中,AB=AC, .
求证: .
(2)证明上述命题.
24受新冠肺炎疫情影响,口罩、体温计、消毒液等一度紧缺,某药店用3200元采购一批耳温计(测量体温的),上市后发现供不应求,很快销售完了,该药店又去采购第二批同样的耳温计,进货价比第一批贵了5元,该店用了9900元,所购数量是第一批的3倍.
(1)求第一批采购的耳温计单价是多少元?
(2)若该药店按每个耳温计的售价为210元,销售光这两批耳温计,总共获利多少元?
25在三角形纸片ABC中,∠ABC=90°,∠A=30°,AC=4,点E在AC上,AE=3.将三角形纸片ABC按图中方式折叠,使点A的对应点A′落在AB的延长线上,折痕为ED,A'E交BC于点F.
(1)求∠CFE的度数;
(2)求BF的长度.
26我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若BD=2AD=2,试求线段CD的长度.
●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
●推广应用
如图3,等腰△ABC为勾股高三角形,其中AB=AC>BC,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若CE=a,试求线段DE的长度.
参考答案
一.选择题
1.
A.
2.
C.
3.
D.
4.
B.
5.
B.
6.
A.
7.
B.
8.
C.
9.
C.
10.
B.
11.D.
12.
A.
13.
B.
14.
C.
15.
A.
16.
C.
二.填空题
17.
12.
18.﹣5.
19.
5.
三、解答题
20
解:(1)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,
∴5a+2=27,3a+b﹣1=16,
∴a=5,b=2;
∵,c是的整数部分,∴c=3;
(2)3a﹣b+c=15﹣2+3=16,16的平方根是±4.
21
解:有错误.改正:
假设AC=BC,则∠A=∠B,又∠C=90°,
所以∠B=∠A=45°,这与∠A≠45°矛盾,所以AC=BC不成立,所以AC≠BC.
22
解:原式=[﹣]÷
=(﹣)?
=?
=,
当x=2时,
原式==3.
23
解:(1)已知:在△ABC中,AB=AC,CD⊥AB于D,
求证:∠BCD=∠A.
故答案为:CD⊥AB于D;∠BCD=∠A;
(2)证明:∵AB=AC,
∴∠B=∠ACB=(180°﹣∠A)=90°﹣∠A,
∵CD⊥AB,
∴∠ACD=90°﹣∠A,
∴∠BCD=∠ACB﹣∠ACD=(90°﹣∠A)﹣(90°﹣∠A)=∠A.
24
解:(1)设第一批采购的耳温计的单价为x元,则第二批采购的耳温计的单价是(x+5)元,
依题意,得:,
解得:x=160,
经检验,x=160是原方程的解,且符合题意,
答:第一批采购的耳温计的单价是160元;
(2)第一批采购的耳温计的数量为3200÷160=20(个),第二批采购的耳温计数量为20×3=60(个),
∴销售完这两批耳温计共获利210×(20+60)﹣3200﹣9900=3700元.
答:销售光这两批耳温计,总共获利3700元.
25
解:(1)由折叠的性质的:∠A′=∠A=30°,
∵∠ABC=90°,点A′落在AB的延长线上,
∴∠A′BF=180°﹣∠ABC=90°,
∴∠A′FB=90°﹣∠A′=60°,
由对顶角相等得:∠CFE=∠A′FB=60°;
(2)∵AC=4,AE=3,∴CE=AC﹣AE=1,
在△ABC中,∠ABC=90°,∠A=30°,
∴∠C=90°﹣∠A=60°,
由(1)知,∠CFE=60°,
∴△CEF是等边三角形,
∴EF=CE=1,
由折叠的性质得:A′E=AE=3,∠A′=∠A=30°,
∴A′F=A′E﹣EF=2,
则在Rt△A′BF中,BF=A′F=×2=1.
26
直角三角形是勾股高三角形.
故答案为是.
②如图1中,根据勾股定理可得:CB2=CD2+4,CA2=CD2+1,
于是CD2=(CD2+4)﹣(CD2+1)=3,
∴CD=.
●深入探究:
如图2中,由CA2﹣CB2=CD2可得:CA2﹣CD2=CB2,而CA2﹣CD2=AD2,
∴AD2=CB2,
即AD=CB;
●推广应用:
过点A向ED引垂线,垂足为G,
∵“勾股高三角形”△ABC为等腰三角形,且AB=AC>BC,
∴只能是AC2﹣BC2=CD2,由上问可知AD=BC……①.
又ED∥BC,∴∠1=∠B……②.
而∠AGD=∠CDB=90°……③,
∴△AGD≌△CDB(AAS),
∴DG=BD.
易知△ADE与△ABC均为等腰三角形,
根据三线合一原理可知ED=2DG=2BD.
又AB=AC,AD=AE,
∴BD=EC=a,
∴ED=2a.
一、选择题(本大题含16个小题;每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列式子中,是分式的是( )
A.
B.
C.﹣
D.
2.已知△ABC≌△DEF,∠A=30°,∠F=85°,则∠B的度数是( )
A.30°
B.85°
C.65°
D.55°
3.下列计算正确的是( )
A.=±7
B.=﹣7
C.=1
D.=
4.在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )
A.
B.
C.
D.
5.若分式的值为0,则x的值为( )
A.±1
B.﹣1
C.1
D.±2
6.如图,已知AC=DB,下列四个条件:①∠A=∠D;②∠ABD=∠DCA;③∠ACB=∠DBC;④∠ABC=∠DCB.其中能使△ABC≌△DCB的有( )
A.1个
B.2个
C.3个
D.4个
7.下列二次根式中,能与合并的是( )
A.
B.
C.
D.
8.如图,在△ABC中.∠C=90°,∠CAB=60°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB,AC于点E、F;②分别以点E、F为圆心,大于EF长为半径画弧,两弧交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )
A.40°
B.50°
C.60°
D.70°
9.把分式(a,b,c均为正)中的b、c的值都扩大为原来的3倍,则分式的值( )
A.不变
B.变为原来的3倍
C.变为原来的
D.变为原来的
10.如图,在△ABC中,BC=10cm,AB的垂直平分线交AB于点D,交边AC于点E,若△BCE的周长等于22cm,则AC的长度等于( )
A.10cm
B.12cm
C.22cm
D.32cm
11.下列计算正确的是( )
A.÷=
B.﹣=
C.+=
D.×=
12.如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是( )
A.12cm
B.16cm
C.18cm
D.20cm
13.数轴上表示下列各数的点,能落在A、B两个点之间的是( )
A.﹣
B.
C.
D.
14.如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )
A.2个
B.3个
C.4个
D.5个
15.老师出了一道题:计算+,对于下面这三名同学的做法,你的判断是( )
乐乐的做法是:原式=﹣==;
淇淇的做法是:原式=(x+3)(x﹣2)+(2﹣x)=x2+x﹣6+2﹣x=x2﹣4;
嘉嘉的做法是:原式=﹣=﹣==1.
A.嘉嘉的做法是正确的
B.淇淇的做法是正确的
C.乐乐的做法是正确的
D.三名同学的做法均不正确
16.如图,要使宽为2米的矩形平板车ABCD通过宽为2米的等宽的直角通道,则平板车的长最多为( )
A.2
B.2
C.4
D.4
二、填空题(本大题含3个小题:17、18小题每题3分,19小题每空2分,共10分)
17.已知,.则代数式x2+y2﹣2xy的值为
.
18.关于x的方程﹣=2有增根,则m的值为
.
19如图,长方体盒子的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着盒子的表面从点A到点B.
(1)蚂蚁爬行的最短距离是 cm;
(2)若从C处想盒子里面插入一根吸管,要使吸管不落入盒子中,吸管应不少于 cm.
三、解答题(本大题含7小题,共计58分,解答题要求写出必要的解题过程)
20已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
21阅读下列文字,回答问题.
题目:在Rt△ABC中,∠C=90°,若∠A≠45°,所以AC≠BC.
证明:假设AC=BC,因为∠A≠45°,∠C=90°,所以∠A≠∠B.
所以AC≠BC,这与假设矛盾,所以AC≠BC.
上面的证明有没有错误?若没有错误,指出其证明的方法;若有错误,请予以纠正.
22先化简(﹣)÷,然后从0,1,2中选取一个合适的x值代入求值.
23求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半.
(1)在图中按照下面“已知”的要求,画出符合题意的图形,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.
已知:在△ABC中,AB=AC, .
求证: .
(2)证明上述命题.
24受新冠肺炎疫情影响,口罩、体温计、消毒液等一度紧缺,某药店用3200元采购一批耳温计(测量体温的),上市后发现供不应求,很快销售完了,该药店又去采购第二批同样的耳温计,进货价比第一批贵了5元,该店用了9900元,所购数量是第一批的3倍.
(1)求第一批采购的耳温计单价是多少元?
(2)若该药店按每个耳温计的售价为210元,销售光这两批耳温计,总共获利多少元?
25在三角形纸片ABC中,∠ABC=90°,∠A=30°,AC=4,点E在AC上,AE=3.将三角形纸片ABC按图中方式折叠,使点A的对应点A′落在AB的延长线上,折痕为ED,A'E交BC于点F.
(1)求∠CFE的度数;
(2)求BF的长度.
26我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若BD=2AD=2,试求线段CD的长度.
●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
●推广应用
如图3,等腰△ABC为勾股高三角形,其中AB=AC>BC,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若CE=a,试求线段DE的长度.
参考答案
一.选择题
1.
A.
2.
C.
3.
D.
4.
B.
5.
B.
6.
A.
7.
B.
8.
C.
9.
C.
10.
B.
11.D.
12.
A.
13.
B.
14.
C.
15.
A.
16.
C.
二.填空题
17.
12.
18.﹣5.
19.
5.
三、解答题
20
解:(1)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,
∴5a+2=27,3a+b﹣1=16,
∴a=5,b=2;
∵,c是的整数部分,∴c=3;
(2)3a﹣b+c=15﹣2+3=16,16的平方根是±4.
21
解:有错误.改正:
假设AC=BC,则∠A=∠B,又∠C=90°,
所以∠B=∠A=45°,这与∠A≠45°矛盾,所以AC=BC不成立,所以AC≠BC.
22
解:原式=[﹣]÷
=(﹣)?
=?
=,
当x=2时,
原式==3.
23
解:(1)已知:在△ABC中,AB=AC,CD⊥AB于D,
求证:∠BCD=∠A.
故答案为:CD⊥AB于D;∠BCD=∠A;
(2)证明:∵AB=AC,
∴∠B=∠ACB=(180°﹣∠A)=90°﹣∠A,
∵CD⊥AB,
∴∠ACD=90°﹣∠A,
∴∠BCD=∠ACB﹣∠ACD=(90°﹣∠A)﹣(90°﹣∠A)=∠A.
24
解:(1)设第一批采购的耳温计的单价为x元,则第二批采购的耳温计的单价是(x+5)元,
依题意,得:,
解得:x=160,
经检验,x=160是原方程的解,且符合题意,
答:第一批采购的耳温计的单价是160元;
(2)第一批采购的耳温计的数量为3200÷160=20(个),第二批采购的耳温计数量为20×3=60(个),
∴销售完这两批耳温计共获利210×(20+60)﹣3200﹣9900=3700元.
答:销售光这两批耳温计,总共获利3700元.
25
解:(1)由折叠的性质的:∠A′=∠A=30°,
∵∠ABC=90°,点A′落在AB的延长线上,
∴∠A′BF=180°﹣∠ABC=90°,
∴∠A′FB=90°﹣∠A′=60°,
由对顶角相等得:∠CFE=∠A′FB=60°;
(2)∵AC=4,AE=3,∴CE=AC﹣AE=1,
在△ABC中,∠ABC=90°,∠A=30°,
∴∠C=90°﹣∠A=60°,
由(1)知,∠CFE=60°,
∴△CEF是等边三角形,
∴EF=CE=1,
由折叠的性质得:A′E=AE=3,∠A′=∠A=30°,
∴A′F=A′E﹣EF=2,
则在Rt△A′BF中,BF=A′F=×2=1.
26
直角三角形是勾股高三角形.
故答案为是.
②如图1中,根据勾股定理可得:CB2=CD2+4,CA2=CD2+1,
于是CD2=(CD2+4)﹣(CD2+1)=3,
∴CD=.
●深入探究:
如图2中,由CA2﹣CB2=CD2可得:CA2﹣CD2=CB2,而CA2﹣CD2=AD2,
∴AD2=CB2,
即AD=CB;
●推广应用:
过点A向ED引垂线,垂足为G,
∵“勾股高三角形”△ABC为等腰三角形,且AB=AC>BC,
∴只能是AC2﹣BC2=CD2,由上问可知AD=BC……①.
又ED∥BC,∴∠1=∠B……②.
而∠AGD=∠CDB=90°……③,
∴△AGD≌△CDB(AAS),
∴DG=BD.
易知△ADE与△ABC均为等腰三角形,
根据三线合一原理可知ED=2DG=2BD.
又AB=AC,AD=AE,
∴BD=EC=a,
∴ED=2a.
同课章节目录
