高一数学 第一章末整合提升 师

中小学教育资源及组卷应用平台
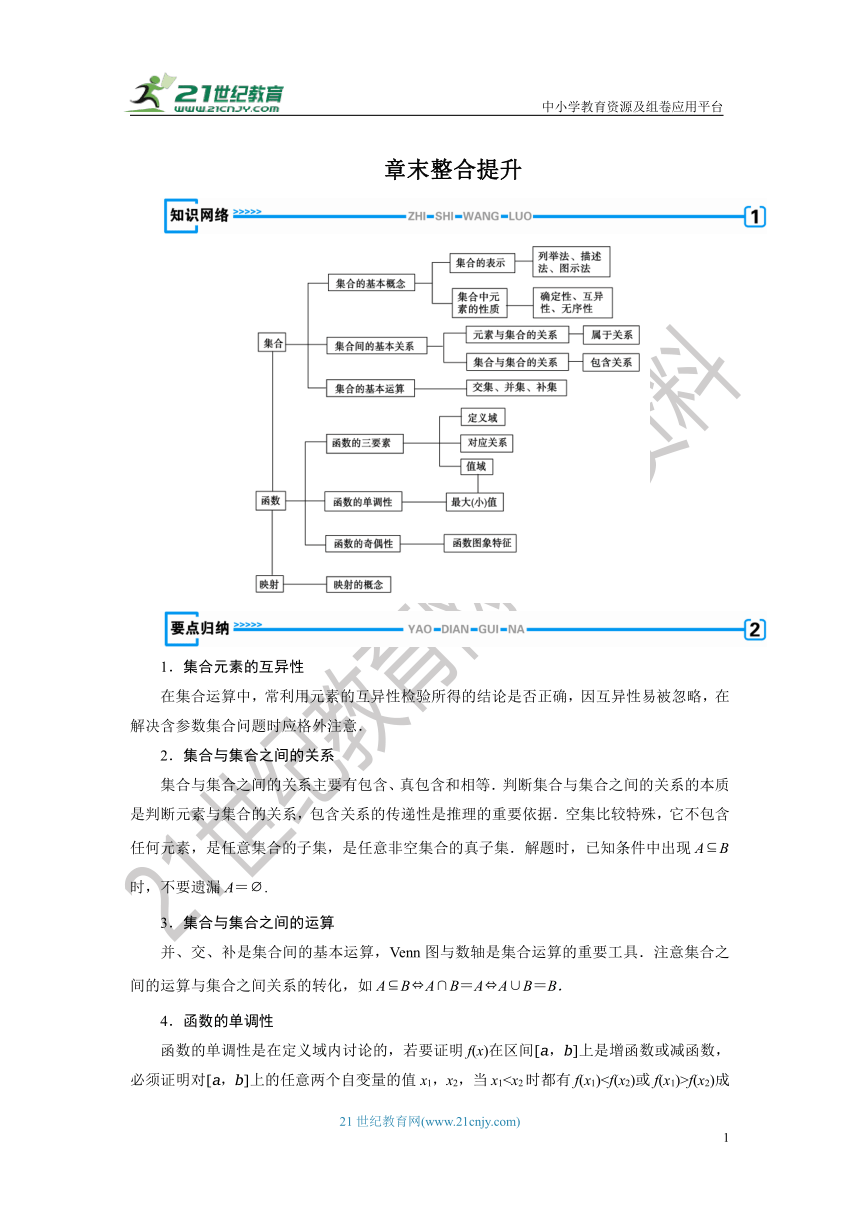
章末整合提升
1．集合元素的互异性
在集合运算中，常利用元素的互异性检验所得的结论是否正确，因互异性易被忽略，在解决含参数集合问题时应格外注意．
2．集合与集合之间的关系
集合与集合之间的关系主要有包含、真包含和相等．判断集合与集合之间的关系的本质是判断元素与集合的关系，包含关系的传递性是推理的重要依据．空集比较特殊，它不包含任何元素，是任意集合的子集，是任意非空集合的真子集．解题时，已知条件中出现A?B时，不要遗漏A＝?.
3．集合与集合之间的运算
并、交、补是集合间的基本运算，Venn图与数轴是集合运算的重要工具．注意集合之间的运算与集合之间关系的转化，如A?B?A∩B＝A?A∪B＝B．
4．函数的单调性
函数的单调性是在定义域内讨论的，若要证明f(x)在区间[a，b]上是增函数或减函数，必须证明对[a，b]上的任意两个自变量的值x1，x2，当x1f(x2)成立；若要证明f(x)在区间[a，b]上不是单调函数，只要举出反例，即只要找到两个特殊的x1，x2，不满足定义即可．单调函数具有下面性质：设函数f(x)定义在区间I上，且x1，x2∈I，则
(1)若函数f(x)在区间I上是单调函数，则x1＝x2?f(x1)＝f(x2)．
(2)若函数f(x)在区间I上是单调函数，则方程f(x)＝0在区间I上至多有一个实数根．
(3)若函数f(x)与g(x)在同一区间的单调性相同，则在此区间内，函数f(x)＋g(x)亦与它们的单调性相同．
函数单调性的判断方法：①定义法；②图象法．
5．函数的奇偶性
判定函数奇偶性，一是用其定义判断，即先看函数f(x)的定义域是否关于原点对称，再检验f(－x)与f(x)的关系；二是用其图象判断，考查函数的图象是否关于原点或y轴对称去判断，但必须注意它是函数这一大前提．
专题一　?集合学习中的注意点剖析
集合主要考查同学们对集合基本概念的认识和理解，以及对集合语言和集合思想的运用．由于集合中的概念较多，逻辑性强，关系复杂，联系广泛，因而同学们在学习过程中常会不知不觉地出错，下面对集合学习中的注意点进行剖析．
1．注意正确理解、运用集合语言
典例1　(1)设集合A＝{x|y＝x2}，B＝{(x，y)|y＝x2}，则A∩B＝__?__；
(2)设集合M＝{y|y＝x2＋1，x∈R}，N＝{y|y＝x＋1，x∈R}，则M∩N＝(　D　)
A．(0,1)，(0,2)　　　
B．{(0,1)，(0,2)}
C．{y|y＝1或y＝2}
D．{y|y≥1}
[分析]　首先分析两个问题中集合中的元素特征，再求交集．
[解析]　(1)集合A中的元素为数，即表示二次函数y＝x2自变量的取值集合；集合B中的元素为点，即表示抛物线y＝x2上的点的集合．这两个集合不可能有相同的元素，故A∩B＝?.
(2)集合M，N的元素都是数，即分别表示定义域为实数集R时，函数y＝x2＋1与y＝x＋1的值域，不是数对或点，故选项A，B错误．而M＝{y|y＝x2＋1，x∈R}＝{y|y≥1}，N＝{y|y∈R}，所以M∩N＝M.故选D．
『规律方法』　学习集合知识，要加强对集合中元素的认识与识别，注意区分数集与点集，知道集合的元素是什么是进行集合运算的前提．另外，集合语言的表达和转化是必须掌握的．
2．注意元素的互异性
典例2　已知1∈{a＋2，(a＋1)2，a2＋3a＋3}，求实数a的值．
[解析]　由题意a＋2＝1，或(a＋1)2＝1，或a2＋3a＋3＝1，解得a＝－1，或a＝－2，或a＝0.
当a＝－2时，(a＋1)2＝a2＋3a＋3＝1，不符合元素的互异性这一特点，故a≠－2.
同理a≠－1.故a＝0.∴实数a的值为0.
『规律方法』　集合中的元素具有确定性、互异性、无序性．在解含有参数的集合问题时，忽视元素(或参数)的特性，往往容易出现错误，要注意解题后的代入检验．
3．注意空集的特殊性
典例3　已知全集U＝{1,2,3,4,5}，A＝{x|x2－4x＋p＝0}，求?UA．
[分析]　符号?UA隐含了A?U，注意不要忘记A＝?的情形．
[解析]　当A＝?时，方程x2－4x＋p＝0无实数解．
此时Δ＝16－4p＜0，∴p＞4，
∴?UA＝?U?＝U＝{1,2,3,4,5}．
当A≠?时，方程x2－4x＋p＝0的两个根x1，x2(x1＜x2)，必须来自于U.
由于x1＋x2＝4，所以x1＝x2＝2或x1＝1，x2＝3.
当x1＝x2＝2时，p＝4，此时A＝{2}，?UA＝{1,3,4,5}；
当x1＝1，x2＝3时，p＝3，此时A＝{1,3}，?UA＝{2,4,5}．
综上所述，当p＞4时，?UA＝{1,2,3,4,5}；
当p＝4时，?UA＝{1,3,4,5}；
当p＝3时，?UA＝{2,4,5}．
『规律方法』　求集合的补集时，不要忘记?的情形．分类讨论是重要的数学思想方法之一，在集合的有关问题中常常用到．
专题二　?函数概念与性质
1．求函数定义域的类型与方法
(1)已给出函数解析式：函数的定义域是使解析式有意义的自变量的取值集合．
(2)实际问题：求函数的定义域既要考虑解析式有意义，还应考虑使实际问题有意义．
(3)复合函数问题：
①若f(x)的定义域为[a，b]，f[g(x)]的定义域应由a≤g(x)≤b解出；
②若f[g(x)]的定义域为[a，b]，则f(x)的定义域为g(x)在[a，b]上的值域．
[注意]　①f(x)中的x与f[g(x)]中的g(x)地位相同；②定义域是自变量x的允许取值范围．
典例4　(1)函数f(x)＝＋(x－3)0的定义域是(　D　)
A．(－1，＋∞)　　　　　
B．(－1,3)
C．(3，＋∞)
D．(－1,3)∪(3，＋∞)
(2)已知函数f(x)的定义域为(－1,0)，则函数f(2x＋1)的定义域为(　B　)
A．(－1,1)
B．(－1，－)
C．(－1,0)
D．(，1)
[解析]　(1)由题意得，，解得x>－1且x≠3.
∴f(x)的定义域为(－1,3)∪(3，＋∞)．
(2)∵函数f(x)的定义域为(－1,0)，∴－1<2x＋1<0，解得－12．二次函数的单调性
二次函数的单调性关键在于开口方向和对称轴与区间的位置关系．
典例5　已知f(x)＝x2＋2(a－1)x－a＋2，分别求下列条件下a的取值范围．
(1)函数f(x)的减区间为(－∞，－1]；
(2)函数f(x)在(－∞，－1]上递减；
(3)函数f(x)在[－1,2]上单调．
[分析]　此题关键在于对单调区间的理解，主要由对称轴与区间的位置决定．
[解析]　函数f(x)＝x2＋2(a－1)x－a＋2的对称轴为x＝1－a.
(1)由于减区间为(－∞，－1]，因此，1－a＝－1，
∴a＝2.
(2)由于函数在(－∞，－1]上递减，应满足1－a≥－1，∴a≤2.
(3)由于函数在[－1,2]上单调，应满足1－a≤－1或1－a≥2，∴a≥2或a≤－1.
3．二次函数的区间最值
解决二次函数的区间最值问题的思路是：抓住“三点一轴”，三点是指区间两个端点和中点，一轴指的是对称轴．结合配方法，根据函数的单调性及分类整合思想即可解决问题．下面通过例题详细分析此类问题的解法．
(1)轴定区间定
典例6　当－2≤x≤2时，求函数y＝x2－2x－3的最大值和最小值．
[分析]　作出函数图象在所给范围的草图(画出对称轴)，观察图象的最高点和最低点，由此得到函数的最大值、最小值及函数取到最值时相应自变量x的值．
[解析]　y＝x2－2x－3＝(x－1)2－4，作出函数的图象如图．
∵－2≤x≤2，∴当x＝1时，ymin＝－4，当x＝－2时，ymax＝9－4＝5.
[点评]　本题已知二次函数在自变量x的给定区间[m，n]上的图象是抛物线的一段，那么最高点的纵坐标即为函数的最大值，最低点的纵坐标即为函数的最小值．
(2)轴动区间定
典例7　已知函数f(x)＝x2＋2ax＋2，求f(x)在[－5，5]上的最大值与最小值．
[分析]　区间定，对称轴不定时，一般解法为：分别把对称轴平移至定区间的左侧、右侧及之间进行讨论，从而确定最值是在端点处取得还是在顶点处取得．本题中函数的对称轴为直线x＝－a，位置不确定，所以应按对称轴与区间[－5,5]的相对位置进行分类讨论．
[解析]　f(x)＝x2＋2ax＋2＝(x＋a)2＋2－a2，x∈[－5,5]，对称轴为直线x＝－a.
(1)当－a＜－5，即a＞5时，函数f(x)在[－5,5]上单调递增，如图(1)，
∴f(x)max＝f(5)＝52＋2a×5＋2＝27＋10a，
f(x)min＝f(－5)＝(－5)2＋2a×(－5)＋2＝27－10a.
(2)当－5≤－a＜0，即0＜a≤5时，如图(2)．
∴f(x)max＝f(5)＝52＋2a×5＋2＝27＋10a，
f(x)min＝f(－a)＝2－a2.
(3)当0≤－a≤5，即－5≤a≤0时，如图(3)，
∴f(x)max＝f(－5)＝(－5)2＋2a×(－5)＋2＝27－10a，
f(x)min＝f(－a)＝2－a2.
(4)当－a＞5，即a＜－5时，如图(4)，
∴f(x)max＝f(－5)＝(－5)2＋2a×(－5)＋2＝27－10a，
f(x)min＝f(5)＝27＋10a.
综上知，f(x)max＝.
f(x)min＝.
『规律方法』　(1)函数f(x)在[a，b]上单调递增时，f(x)max＝f(b)；函数f(x)在[a，b]上单调递减时，f(x)max＝f(a)；函数f(x)在[a，b]上不是单调函数时，找出图象上最高点的纵坐标，即为函数f(x)的最大值，图象上最低点的纵坐标，即为函数f(x)的最小值．
(2)二次函数在给定区间[m，n]上的最值求解，常见的有以下四种情况：
①对称轴与区间[m，n]均是确定的；
②动轴定区间，即对称轴不确定，区间[m，n]是确定的；
③定轴动区间，即对称轴是确定的，区间[m，n]不确定；
④动轴动区间，即对称轴不确定，区间[m，n]也不确定．
以上四种情况，对于①可数形结合，较易解决．对于②和③，应按对称轴在区间的左侧、内部、右侧分三类，结合其图象特征分别求解．④可让区间不动，按对称轴在区间左侧、内部、右侧进行讨论，有时在区间内部还可分为两种情况：m≤x≤和＜x≤n进行讨论．
(3)轴定区间动
典例8　二次函数f(x)＝x2－2x＋2，当x∈[t，t＋1]时，求f(x)的最小值g(t)．
[分析]　因为对称轴固定，区间不定，此题可从三个方面进行讨论：①区间在对称轴左侧；②区间在对称轴右侧；③对称轴在区间内．
[解析]　二次函数f(x)＝x2－2x＋2的图象开口向上，对称轴为直线x＝1.
当t＞1时，f(x)在[t，t＋1]上单调递增，则g(t)＝f(t)＝t2－2t＋2；
当t≤1≤t＋1，即0≤t≤1时，则g(t)＝f(1)＝1－2＋2＝1；
当t＋1＜1，即t＜0时，f(x)在[t，t＋1]上单调递减，则g(t)＝f(t＋1)＝t2＋1.
综上所述，f(x)min＝g(t)＝.
『规律方法』　对称轴确定，区间不确定时，可以把区间看成可移动的，分别移至对称轴的不同位置进行讨论．
4．抽象函数问题
抽象函数是相对具体的函数而言的，是指没有给出具体的函数解析式或对应关系，只是给出函数所满足的一些条件或性质的一类函数．
抽象函数问题一般是由所给的条件或性质，讨论函数的其他性质，如单调性、奇偶性，或是求函数值、解析式等．下面对抽象函数的单调性、奇偶性问题举例说明．
典例9　设函数f(x)对任意实数x，y都有f(x＋y)＝f(x)＋f(y)，且x>0时，f(x)<0，f(1)＝－2.
(1)求证：f(x)是奇函数；
(2)求f(x)在[－3,3]上的最大值与最小值．
[解析]　(1)证明：令x＝y＝0，得f(0)＋f(0)＝f(0)，
∴f(0)＝0.
又令y＝－x，得f(0)＝f(x)＋f(－x)＝0，
∴f(－x)＝－f(x)，∴f(x)是奇函数．
(2)解：在取x1，x2∈R，且x10，
于是f(x2)－f(x1)＝f(x2)＋f(－x1)
＝f(x2－x1)<0，
∴f(x1)>f(x2)，∴f(x)在R上是减函数，
∴f(x)的最大值为f(－3)＝－f(3)＝－3f(1)
＝(－3)×(－2)＝6，
f(x)的最小值为f(3)＝－f(－3)＝－6.
专题三　?数学思想方法
1．数形结合思想
数形结合思想，其实质是将抽象的数学语言与直观的图形结合起来，使抽象思维与形象思维相结合，使问题化难为易、化抽象为具体．
典例10　已知函数f(x)＝x2－2|x|－1(－3≤x≤3)．
(1)求证：f(x)是偶函数；
(2)画出这个函数的图象；
(3)指出函数f(x)的单调区间，并说明在各个单调区间上f(x)的单调性；
(4)求函数f(x)的值域．
[解析]　(1)证明：∵函数定义域[－3,3]关于原点对称，且f(－x)＝(－x)2－2|－x|－1＝x2－2|x|－1＝f(x)，
∴f(x)为偶函数．
(2)当x≥0时，f(x)＝x2－2x－1＝(x－1)2－2；
当x<0时，f(x)＝x2＋2x－1＝(x＋1)2－2.
即f(x)＝
根据分段函数的作图方法，可得函数图象如上图所示．
(3)函数f(x)的单调区间为[－3，－1)，[－1,0)，[0,1)，[1,3]．
f(x)在[－3，－1)，[0,1)上为减函数；在[－1,0)，[1,3]上为增函数．
(4)f(x)图象在y轴上的纵投影为[－2,2]，
故函数f(x)的值域为[－2,2]．
『规律方法』　(1)含绝对值符号的函数图象的画法：
①根据绝对值定义去掉绝对值符号，将原函数化为分段函数；
②依次作每一段的图象．
(2)注意事项：
①若原函数具有奇偶性，可利用奇(偶)函数的对称性作图象；
②通常令绝对值号内的式子等于0，以求得讨论的分界点．
2．分类讨论思想
分类讨论问题的实质是：把整体问题化为部分来解决，从而增加了题设条件，这也是解决分类问题的指导思想，根据题意，要适当划分讨论的层次．
解分类讨论问题的步骤是：
(1)确定分类讨论的对象，即对哪个参数进行讨论；
(2)对所讨论的对象要进行合理的分类(分类时要做到不重复、不遗漏，标准要统一，分层不越级)；
(3)逐类讨论，即对各类问题逐类讨论，逐个解决；
(4)归纳总结，即对各类问题总结归纳，得出结论．
典例11　设a为实数，函数f(x)＝x2＋|x－a|＋1，x∈R.
(1)讨论f(x)的奇偶性；
(2)求f(x)的最小值．
[分析]　(1)根据函数奇偶性的定义知，判断某函数是否具有奇偶性，应先判断其定义域是否关于原点对称，再看是否有f(－x)±f(x)＝0；若要证明某函数不具有奇偶性，则只需举出反例即可；(2)求f(x)的最小值，首先去掉绝对值符号，然后根据对称轴与所研究区间的相对位置关系进行讨论．
[解析]　(1)当a＝0时，函数f(－x)＝(－x)2＋|－x|＋1＝f(x)，此时f(x)为偶函数．
当a≠0时，f(a)＝a2＋1，f(－a)＝a2＋2|a|＋1，－f(a)＝－a2－1，f(－a)≠f(a)，f(－a)≠－f(a)，此时f(x)既不是奇函数也不是偶函数．
(2)①当x≤a时，函数f(x)＝x2－x＋a＋1＝(x－)2＋a＋.
若a≤，则函数f(x)在(－∞，a]上单调递减，
从而函数f(x)在(－∞，a]上的最小值为f(a)＝a2＋1；
若a>，则函数f(x)在(－∞，a]上最小值为f()＝＋a.
②当x≥a时，函数f(x)＝x2＋x－a＋1＝(x＋)2－a＋.
若a≤－，则函数f(x)在[a，＋∞)上的最小值为f(－)＝－a；
若a>－，则函数f(x)在[a，＋∞)上单调递增，
从而函数f(x)在[a，＋∞)上的最小值为f(a)＝a2＋1.
综上，当a≤－时，函数f(x)的最小值是－a；
当－当a>时，函数f(x)的最小值是＋a.
3．转化与化归思想
为了解决问题的方便，我们经常把所给问题进行形式上的变化，把要解决的问题转化为已经解决的问题．这种解决问题的思想就是转化与化归思想．
典例12　对任意x∈[1，＋∞)，不等式x2＋2x－a>0恒成立．求实数a的取值范围．
[解析]　由已知x∈[1，＋∞)，x2＋2x－a>0恒成立，
即a令g(x)＝x2＋2x，x∈[1，＋∞)，
则原问题可转化为a小于g(x)在[1，＋∞)上的最小值问题．
∵g(x)＝(x＋1)2－1的图象的对称轴为x＝－1，
∴函数g(x)在[1，＋∞)上是增函数．
∴当x＝1时，g(x)取最小值，g(1)＝3.∴a<3.
∴实数a的取值范围为{a|a<3}．
『规律方法』　aA级　基础巩固
一、选择题
1．下列集合中，不同于另外三个集合的是(　B　)
A．{x|x＝1}　　　　　　
B．{x|x2＝1}
C．{1}
D．{y|(y－1)2＝0}
[解析]　{x|x2＝1}＝{－1,1}，另外三个集合都是集合{1}，故选B．
2．(2019·山东济宁市高一期末测试)已知集合A＝{x|－2A．{－2，－1,0,1}
B．{－2，－1,0}
C．{－1,0,1}
D．{－1,0}
[解析]　A∩B＝{x|－23．(2019·山东莒县一中高一期末测试)已知函数f(x)＝，则f[f(1)]等于(　B　)
A．2
B．3
C．4
D．5
[解析]　∵x<2时，f(x)＝2x＋1，
∴f(1)＝2×1＋1＝3，
又∵x≥2时，
f(x)＝x2－2x，
∴f[f(1)]＝f(3)＝32－2×3＝3.
4．设f(x)是定义在R上的奇函数，当x≥0时，f(x)＝2x＋b，则f(－1)等于(　C　)
A．0
B．2
C．－2
D．1
[解析]　∵x≥0时，f(x)＝2x＋b，且f(x)为奇函数，
∴f(0)＝0，∴b＝0.
∴f(x)＝2x，∴f(－1)＝－f(1)＝－2.
5．已知二次函数y＝ax2＋bx＋c满足a>b>c且a＋b＋c＝0，那么它的图象可能是图中的(　A　)
[解析]　∵a>b>c，a＋b＋c＝0，
∴a>0，c<0，∴图象开口向上，与y轴交于负半轴，故排除B、C．
∵当x＝1时，y＝0，∴A正确．
6．若函数f(x)＝是定义在R上的减函数，则a的取值范围为(　A　)
A．[，)
B．(0，)
C．[，＋∞)
D．(－∞，]∪[，＋∞)
[解析]　由f(x)＝是R上的减函数知，
解得≤a<.
二、填空题
7．(2019·安徽太和中学高一期中测试)已知集合A＝{0,3,4m－4}，集合B＝{3，m2}，若B?A，则实数m＝__0或2__.
[解析]　∵B?A，∴m2＝0或m2＝4m－4，
当m2＝0时，m＝0，A＝{－4,0,3}，B＝{0,3}，满足B?A．
当m2＝4m－4时，m2－4m＋4＝0，m＝2，A＝{0,3,4}，B＝{3,4}满足B?A．
综上可知m＝0或2.
8．若函数f(x)满足f(2x＋1)＝3－2x，则f(x)的解析式为__f(x)＝4－x__.
[解析]　设2x＋1＝t，则x＝，
∴f(t)＝3－2×＝3－t＋1＝4－t.
∴f(x)＝4－x.
三、解答题
9．已知全集为实数集R，集合A＝{x|1≤x≤7}，B＝{x|－2m＋1(1)若m＝5，求A∪B，(?RA)∩B；
(2)若A∩B＝A，求m的取值范围．
[解析]　(1)∵m＝5，∴B＝{x|－9∴A∪B＝{x|－9又?RA＝{x|x<1或x>7}，
∴(?RA)∩B＝{x|－9(2)∵A∩B＝A，∴A?B，
∴，即，解得m>7.
∴m的取值范围是{m|m>7}．
B级　素养提升
一、选择题
1．已知集合A＝{y|y＝x2－1，x∈R}，B＝{y|y＝－x2＋2，x∈R}，则A∪B等于(　A　)
A．R
B．{y|－2≤y≤2}
C．{y|y≤－1或y≥2}
D．以上都不对
[解析]　A＝{y|y＝x2－1，x∈R}＝{y|y≥－1}，
B＝{y|y＝－x2＋2，x∈R}＝{y|y≤2}，
∴A∪B＝{y|y≥－1}∪{y|y≤2}＝R.
2．函数f(x2)＝x10＋1，则函数f(x)的解析式为(　B　)
A．f(x)＝x5＋1
B．f(x)＝x5＋1(x≥0)
C．f(x)＝x5＋1(x≥1)
D．f(x)＝x＋1(x≥1)
[解析]　令t＝x2，∴t≥0，∴x10＝t5，
∴f(t)＝t5＋1，∴f(x)＝x5＋1(x≥0)，故选B．
3．已知函数f(x)的定义域为[－2,1]，函数g(x)＝，则g(x)的定义域为(　A　)
A．(－，2]
B．(－1，＋∞)
C．(－，0)∪(0,2)
D．(－，2)
[解析]　由题意，得，∴－4．甲乙两种商品在过去一段时间的价格走势如图所示．假设某人持有资金120万元，他可以在t1至t4的任意时刻买卖这两种商品，且买卖能够立即成交(其他费用忽略不计)，那么他持有的资金最多可变为(　D　)
A．120万元
B．160万元
C．220万元
D．240万元
[解析]　甲在6元时，全部买入，可以买120÷6＝20(万)份，
在t2时刻全部卖出，此时获利20×2＝40万，
乙在4元时买入，可以买(120＋40)÷4＝40(万)份，
在t4时刻全部卖出，此时获利40×2＝80万，共获利40＋80＝120万，即最多可变为120＋120＝240(万元)．
二、填空题
5．已知f(x)＝，若f(x)＝－2，则x＝__或4__.
[解析]　当x≤2时，2x－3＝－2，∴x＝；当x>2时，－x＋2＝－2，∴x＝4.综上可知x＝或4.
6．设函数y＝f(x)对任意正实数x，y都有f(x·y)＝f(x)＋f(y)，已知f(8)＝3，则f()＝____.
[解析]　∵对任意正实数x，y都有f(x·y)＝f(x)＋f(y)，
∴f(8)＝f(2×4)＝f(2)＋f(4)，
又f(4)＝f(2×2)＝f(2)＋f(2)，
∴f(8)＝3f(2)＝3，∴f(2)＝1.
∴f(2)＝f(×)＝f()＋f()＝1，
∴f()＝.
三、解答题
7．(2019·天津和平区高一期中测试)已知函数f(x)＝.
(1)求f(2)的值；
(2)求f(x)的定义域和值域．
[解析]　(1)∵f(x)＝，
∴f(2)＝＝－.
(2)要使f(x)有意义，应满足x＋2≠0，∴x≠－2.
∴f(x)的定义域为{x|x≠－2}．
f(x)＝＝＝1－，
∵≠0，∴1－≠1，
∴f(x)的值域为(－∞，1)∪(1，＋∞)．
8．已知定义在R上的函数y＝f(x)满足f(－x)＝－f(x)，它在(0，＋∞)上是增函数，且f(x)<0，问F(x)＝在(－∞，0)上是增函数还是减函数？证明你的结论．
[解析]　由已知可得，F(x)在(－∞，0)上是减函数．
证明如下：
任取x1，x2∈(－∞，0)，且x1－x2>0.
∵y＝f(x)在(0，＋∞)上是增函数，且f(x)<0，
∴f(－x2)又∵f(－x)＝－f(x)，②
∴f(－x2)＝－f(x2)，f(－x1)＝－f(x1)③
由①②③，得f(x2)>f(x1)>0.F(x1)－F(x2)＝>0，即F(x1)>F(x2)．
∴F(x)＝>0在(－∞，0)上是减函数．
9．定义在(－8,8)上的函数f(x)既为减函数，又为奇函数，解关于a的不等式f(7－a)＋f(5－a)<0.
[解析]　∵f(x)为奇函数，f(7－a)＋f(5－a)<0，
∴f(7－a)<－f(5－a)＝f(a－5)．
又由f(x)在(－8,8)上为减函数，
可得，
∴解得－1∴原不等式的解集为(－1,6)．
21世纪教育网(www.21cnjy.com)