5.6二元一次方程与一次函数同步练习-2021-2022学年北师大版数学八年级上学期(word版含答案)
文档属性
| 名称 | 5.6二元一次方程与一次函数同步练习-2021-2022学年北师大版数学八年级上学期(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 20:20:45 | ||
图片预览


文档简介
初中数学北师大版八年级上学期 第五章 5.6二元一次方程与一次函数
一、单选题
1.如图,以两条直线l1 , l2的交点坐标为解的方程组是(?? )
A.????????????????????B.????????????????????C.????????????????????D.?
2.在同一直角坐标系内,若直线y=2x-1与直线y=-2x+m的交点在第四象限,则m的取值范围是(?? )
A.?m>—1????????????????????????????B.?m<1????????????????????????????C.?—1<m<1????????????????????????????D.?—1≤m≤1
3.已知一次函数 y=x+1y=x+1 和一次函数 的图象的交点坐标是 (3,4)(3,4) ,据此可知方程组 的解为(???? )
A.?{x=3y=4{x=3y=4 ??????????????????????????????B.?{x=4y=3{x=4y=3??????????????????????????????C.???????????????????????????????D.?
4.已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,两函数y=x+5与y=﹣ 1212 x﹣1的图像的交点坐标为(? )
A.?(﹣4,1)??????????????????????B.?(1,﹣4)??????????????????????C.?(4,﹣1)??????????????????????D.?(﹣1,4)
二、填空题
5.若一次函数y=3x-5的图像l1与y=2x+1的图像l2相交于点P,则点P的坐标是(________,________)。
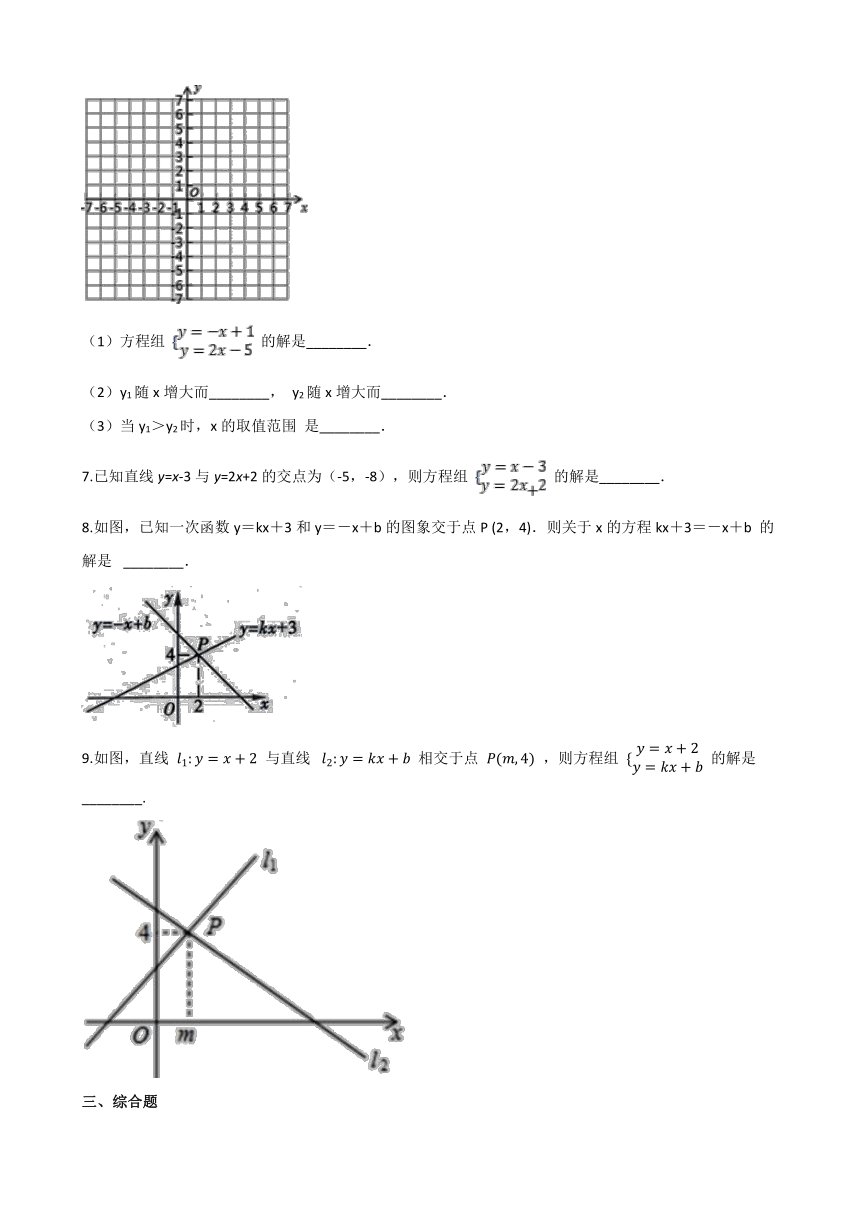
6.画出函数y1=-x+1,y2=2x-5 的图象,利用图象回答下列问题:
(1)方程组 的解是________.
(2)y1随x增大而________, y2随x增大而________.
(3)当y1>y2时,x的取值范围 是________.
7.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组 的解是________.
8.如图,已知一次函数y=kx+3和y=-x+b的图象交于点P (2,4).则关于x的方程kx+3=-x+b 的解是? ________.
9.如图,直线 l1:y=x+2l1:y=x+2 与直线 l2:y=kx+b l2:y=kx+b 相交于点 P(m,4)P(m,4) ,则方程组 {y=x+2y=kx+b{y=x+2y=kx+b 的解是________.
三、综合题
10.为了抗击新冠疫情,我市甲乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨,这批防疫物资将运往A地240吨,B地260吨,运费如下:(单位:吨)
(1)求甲乙两厂各生产了这批防疫多少吨?
(2)设这批物资从乙厂运往A地x吨,全部运往A,B两地的总运费为y元,求y与x之间的函数关系式,并设计使总运费最少的调运方案;
(3)当每吨运费降低m元,( 且m为整数),按(2)中设计的调运方案运输,总运费不超过5200元,求m的最小值.
11.学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元。
(1)分别求一本笔记本和一支钢笔的售价;
(2)若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由。
12.下表是小丽在某路口统计20分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊。
电瓶车
公交车
货车
小轿车
合计(车流总量)
(第一时段)8:50~9:00
m
86
161
(第二时段)9:00~9:10
7n
m
n
99
合计
30
185
(1)根据表格信息,在表格中填写第一时段电瓶车和货车的数量。
(2)在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为170辆。
①求m,n的值。
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加1辆公交车,可减少8辆小轿车和5辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
13.在创建全国文明城市过程中,官渡区决定购买A、B两种树苗对某路段道路进行绿化改造.已知购买A种树苗5棵,B种树苗3棵,需要840元;购买A种树苗3棵,B种树苗5棵,需要760元.
(1)求购买A、B两种树苗每棵各需多少元?
(2)现需购进这两种树苗共100棵,考虑到绿化效果和资金周转,购进A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过10000元,怎样购买所需资金最少?
答案解析部分
一、单选题
1.【答案】 C
2.【答案】 C
3.【答案】 A
4.【答案】 A
二、填空题
5.【答案】 6;13
6.【答案】 (1)
(2)减小;增大
(3)x<2
7.【答案】
8.【答案】 x=2
9.【答案】 {x=2y=4{x=2y=4
三、综合题
10.【答案】 (1)解:设这批防疫物资甲厂生产了a吨,乙厂生产了b吨;
则
解得: {a=200b=300{a=200b=300
答:这批防疫物资甲厂生产了200吨,乙厂生产了300吨;
(2)解:如图,甲、乙两厂调往 A,BA,B 两地的数量如下:
当x=240时运费最小
所以总运费的方案是:甲厂200吨全部运往B地;乙厂运往A地240吨,运往B地60吨.
(3)解:由(2)知:
当x=240时, ,
所以m的最小值为10.
11.【答案】 (1)解:设一本笔记本的售价为x元,一支钢笔的售价为y元,
根据题意,得 {x+4y=1004x+6y=190{x+4y=1004x+6y=190
解得 {x=16y=21{x=16y=21
答:一本笔记本的售价为16元,一支钢笔的售价为21元
(2)解:设笔记本的购买数量为a本,则钢笔的购买数量为(90-a)支,
根据题意,得a≤3(90-a),
解得a≤67.5
购买费用为w=16a+21(90-a)=-5a+1890,
∵-5<0,∴w随着a的增大而减小,
∴当a=67时,w取得最小值为w=1555元。
此时,购买笔记本67本,钢笔23支
12.【答案】 (1)解:第一时段货车的数量为:30-n
第一时段电瓶车的数量为:161-m-86-(30-n)=45-m+n;
(2)解:①由题意得:
解之:m=3n=16m=3n=16
②设第二时段应增加x辆公交车,第二时段的车流量为y辆,
y=7×16+3+16+99+x-(8+5)x=-12x+230,
当y=161时,-12x+230=161
解之:x=534x=534
∵
∴应该增加6辆公交车.
13.【答案】 (1)解:设购买A种树苗每棵需要x元,B种树苗每棵需要y元. 由题意,得 {5x+3y=8403x+5y=760{5x+3y=8403x+5y=760 解得 {x=120y=80{x=120y=80
答:购买A种树苗每棵需要120元,B种树苗每棵需要80元.
(2)解:设购买A种树苗m棵,则购买B种树苗(100-m)棵,购买资金为w元 w=120m+80(100-m)
=40m+8000
由题意,得
解得: ,且m为整数
∵40>0 ,
∴w随m的增大而增大,
∴当m=30时,w最小,此时B种树苗:100-30=70(棵)
答:购买A种树苗30棵,B种树苗70棵,此时购买资金最少
一、单选题
1.如图,以两条直线l1 , l2的交点坐标为解的方程组是(?? )
A.????????????????????B.????????????????????C.????????????????????D.?
2.在同一直角坐标系内,若直线y=2x-1与直线y=-2x+m的交点在第四象限,则m的取值范围是(?? )
A.?m>—1????????????????????????????B.?m<1????????????????????????????C.?—1<m<1????????????????????????????D.?—1≤m≤1
3.已知一次函数 y=x+1y=x+1 和一次函数 的图象的交点坐标是 (3,4)(3,4) ,据此可知方程组 的解为(???? )
A.?{x=3y=4{x=3y=4 ??????????????????????????????B.?{x=4y=3{x=4y=3??????????????????????????????C.???????????????????????????????D.?
4.已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,两函数y=x+5与y=﹣ 1212 x﹣1的图像的交点坐标为(? )
A.?(﹣4,1)??????????????????????B.?(1,﹣4)??????????????????????C.?(4,﹣1)??????????????????????D.?(﹣1,4)
二、填空题
5.若一次函数y=3x-5的图像l1与y=2x+1的图像l2相交于点P,则点P的坐标是(________,________)。
6.画出函数y1=-x+1,y2=2x-5 的图象,利用图象回答下列问题:
(1)方程组 的解是________.
(2)y1随x增大而________, y2随x增大而________.
(3)当y1>y2时,x的取值范围 是________.
7.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组 的解是________.
8.如图,已知一次函数y=kx+3和y=-x+b的图象交于点P (2,4).则关于x的方程kx+3=-x+b 的解是? ________.
9.如图,直线 l1:y=x+2l1:y=x+2 与直线 l2:y=kx+b l2:y=kx+b 相交于点 P(m,4)P(m,4) ,则方程组 {y=x+2y=kx+b{y=x+2y=kx+b 的解是________.
三、综合题
10.为了抗击新冠疫情,我市甲乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨,这批防疫物资将运往A地240吨,B地260吨,运费如下:(单位:吨)
(1)求甲乙两厂各生产了这批防疫多少吨?
(2)设这批物资从乙厂运往A地x吨,全部运往A,B两地的总运费为y元,求y与x之间的函数关系式,并设计使总运费最少的调运方案;
(3)当每吨运费降低m元,( 且m为整数),按(2)中设计的调运方案运输,总运费不超过5200元,求m的最小值.
11.学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元。
(1)分别求一本笔记本和一支钢笔的售价;
(2)若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由。
12.下表是小丽在某路口统计20分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊。
电瓶车
公交车
货车
小轿车
合计(车流总量)
(第一时段)8:50~9:00
m
86
161
(第二时段)9:00~9:10
7n
m
n
99
合计
30
185
(1)根据表格信息,在表格中填写第一时段电瓶车和货车的数量。
(2)在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为170辆。
①求m,n的值。
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加1辆公交车,可减少8辆小轿车和5辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
13.在创建全国文明城市过程中,官渡区决定购买A、B两种树苗对某路段道路进行绿化改造.已知购买A种树苗5棵,B种树苗3棵,需要840元;购买A种树苗3棵,B种树苗5棵,需要760元.
(1)求购买A、B两种树苗每棵各需多少元?
(2)现需购进这两种树苗共100棵,考虑到绿化效果和资金周转,购进A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过10000元,怎样购买所需资金最少?
答案解析部分
一、单选题
1.【答案】 C
2.【答案】 C
3.【答案】 A
4.【答案】 A
二、填空题
5.【答案】 6;13
6.【答案】 (1)
(2)减小;增大
(3)x<2
7.【答案】
8.【答案】 x=2
9.【答案】 {x=2y=4{x=2y=4
三、综合题
10.【答案】 (1)解:设这批防疫物资甲厂生产了a吨,乙厂生产了b吨;
则
解得: {a=200b=300{a=200b=300
答:这批防疫物资甲厂生产了200吨,乙厂生产了300吨;
(2)解:如图,甲、乙两厂调往 A,BA,B 两地的数量如下:
当x=240时运费最小
所以总运费的方案是:甲厂200吨全部运往B地;乙厂运往A地240吨,运往B地60吨.
(3)解:由(2)知:
当x=240时, ,
所以m的最小值为10.
11.【答案】 (1)解:设一本笔记本的售价为x元,一支钢笔的售价为y元,
根据题意,得 {x+4y=1004x+6y=190{x+4y=1004x+6y=190
解得 {x=16y=21{x=16y=21
答:一本笔记本的售价为16元,一支钢笔的售价为21元
(2)解:设笔记本的购买数量为a本,则钢笔的购买数量为(90-a)支,
根据题意,得a≤3(90-a),
解得a≤67.5
购买费用为w=16a+21(90-a)=-5a+1890,
∵-5<0,∴w随着a的增大而减小,
∴当a=67时,w取得最小值为w=1555元。
此时,购买笔记本67本,钢笔23支
12.【答案】 (1)解:第一时段货车的数量为:30-n
第一时段电瓶车的数量为:161-m-86-(30-n)=45-m+n;
(2)解:①由题意得:
解之:m=3n=16m=3n=16
②设第二时段应增加x辆公交车,第二时段的车流量为y辆,
y=7×16+3+16+99+x-(8+5)x=-12x+230,
当y=161时,-12x+230=161
解之:x=534x=534
∵
∴应该增加6辆公交车.
13.【答案】 (1)解:设购买A种树苗每棵需要x元,B种树苗每棵需要y元. 由题意,得 {5x+3y=8403x+5y=760{5x+3y=8403x+5y=760 解得 {x=120y=80{x=120y=80
答:购买A种树苗每棵需要120元,B种树苗每棵需要80元.
(2)解:设购买A种树苗m棵,则购买B种树苗(100-m)棵,购买资金为w元 w=120m+80(100-m)
=40m+8000
由题意,得
解得: ,且m为整数
∵40>0 ,
∴w随m的增大而增大,
∴当m=30时,w最小,此时B种树苗:100-30=70(棵)
答:购买A种树苗30棵,B种树苗70棵,此时购买资金最少
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
