2021-2022学年北师大版数学八年级上学期3.3 轴对称与坐标变化同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级上学期3.3 轴对称与坐标变化同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 285.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 20:24:16 | ||
图片预览



文档简介
初中数学北师大版八年级上学期 第三章 3.3 轴对称与坐标变化
一、单选题
1.在平面直角坐标系中,点 关于x轴对称的点是(??? )
A.?(2,1)(2,1)??????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
2.已知点M (3,﹣2),N(﹣3,﹣2),则直线MN与x轴、y轴的位置关系分别为(? )
A.?平行,垂直???????????????????????B.?平行,平行???????????????????????C.?垂直,平行???????????????????????D.?相交,相交
3.如图,在平面直角坐标系中,点 A(3,m)A(3,m) 在第一象限,若点A关于x轴的对称点B在直线 上,则m的值为(??? )
A.?-1???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
4.平面直角坐标中,已知点P(a , 3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( ???)
A.?(﹣a , 3)??????????????????B.?(a , ﹣3)??????????????????C.?(﹣a+2,3)??????????????????D.?(﹣a+4,3)
二、填空题
5.如图,点 与点 Q(a,b)Q(a,b) 关于直线 对称,则 a+b=a+b= ________.
6.点A(-2,1)关于x轴对称的点的坐标是________.
三、作图题
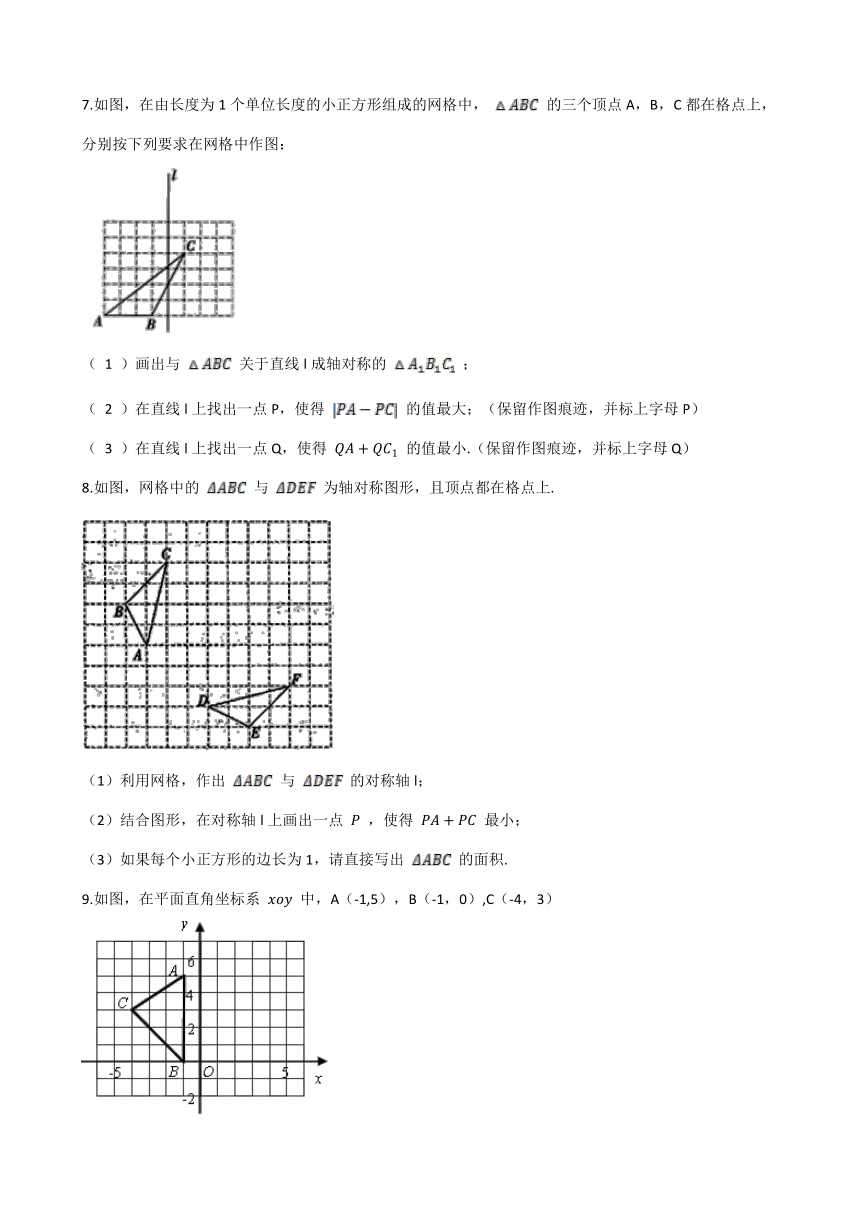
7.如图,在由长度为1个单位长度的小正方形组成的网格中, 的三个顶点A,B,C都在格点上,分别按下列要求在网格中作图:
( 1 )画出与 关于直线l成轴对称的 ;
( 2 )在直线l上找出一点P,使得 的值最大;(保留作图痕迹,并标上字母P)
( 3 )在直线l上找出一点Q,使得 QA+QC1QA+QC1 的值最小.(保留作图痕迹,并标上字母Q)
8.如图,网格中的 与 为轴对称图形,且顶点都在格点上.
(1)利用网格,作出 与 的对称轴l;
(2)结合图形,在对称轴l上画出一点 PP ,使得 PA+PCPA+PC 最小;
(3)如果每个小正方形的边长为1,请直接写出 的面积.
9.如图,在平面直角坐标系 xoyxoy 中,A(-1,5),B(-1,0),C(-4,3)
(1)在图中作出 关于 yy 轴的对称图形 .
(2)写出点 的坐标.
(3)求出 的面积.
10.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
①在如图所示的网格平面内作出平面直角坐标系;
②作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
③P是x轴上的动点,在图中找出使△A′BP周长最短时的点P,直接写出点P的坐标.
四、综合题
11.在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB =OA=3.
(1)求点A、B的坐标;
(2)已知点C(-2,2),求△ BOCBOC 的面积;
(3)点P是第一、三象限角平分线上一点,若 ,求点P的坐标.
?
12.在平面直角坐标系中,有点A(a﹣1,3),B(a+2,2a﹣1)
(1)若线段AB∥x轴,求点A、B的坐标;
(2)当点B到y轴的距离与点A到x轴的距离相等时,求点B所在的象限.
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 A
3.【答案】 C
4.【答案】 D
二、填空题
5.【答案】 -5
6.【答案】 (-2,-1)
三、作图题
7.【答案】 解:(1)如图, 即为所求.
( 2 )如图,连接 AC1AC1 并延长,交直线l于点P,点P即为所求.
∵点C1点C关于直线l对称,
∴ =AC1 ,
∴连接 AC1AC1 并延长,交直线l于点P,点P即为所求.
( 3 )如图,直线 ACAC 与直线l的交点Q即为所求,
∵点C1点C关于直线l对称,
∴ QA+QC1QA+QC1 =QA+QC=AC,
∴直线 ACAC 与直线l的交点Q.
8.【答案】 (1)解:对称轴应为两个三角形对应点连线的中线,故连接CF、DE,找到线段CF、DE的中点,再连接起来,即为所求直线l.
(2)解:如图所示,点P即为所求;
连接CD与l的交点即为点P的位置,因为点A与点D关于l对称,根据两点之间,线段最短可得: PA+PC=PD+PC=CDPA+PC=PD+PC=CD ,即P点即为所求;
(3)解: ABC的面积可由一个矩形,减去三个直角三角形的面积所得,
,
故 ABC的面积为3.
9.【答案】 (1)解:所作图形如图所示:
(2)解:点 A1A1 , B1B1 , C1C1 的坐标分别为(1,5),(1,0),(4,3)
(3)解:∵A(-1,5),B(-1,0),C(-4,3),∴ = =7.5
10.【答案】 解:如图所示,B′(2,1)、点P即为所求点,
设直线A′B1的解析式为y=kx+b(k≠0),
∵A′(4,5),B1(﹣2,﹣1),
∴ 解得 {k=1b=1{k=1b=1
∴直线A′B1的解析式为y=x+1.
∵当y=0时,x+1=0,解得x=﹣1,
∴P(﹣1,0)
四、综合题
11.【答案】 (1)∵OB=OA=3,A、B两点分别在x轴、y轴的正半轴上, ∴A(3,0),B(0,3).
(2) =3.
(3)∵点P是第一、三象限角平分线上,∴设P(a,a). ∵ ,
当 P1P1 在AB的上方第一象限时,
= .
= .
∴ . 整理,得 .∴ a=7a=7 . ∴ P1P1 (7,7).
12.【答案】 (1)∵线段AB∥x轴,
∴2a﹣1=3,
解得:a=2,
故a﹣1=1,a+2=4,
则A(1,3),B(4,3);
(2)∵点B到y轴的距离与点A到x轴的距离相等,
∴|a+2|=3,
解得:a=﹣5或1,
当a=﹣5时
故a+2=﹣3,2a﹣1=﹣11,
故B(﹣3,﹣11)在第三象限,
当a=1时
故a+2=3,2a﹣1=1,
故B(3,1)在第一象限,
综上所述:点B在第一象限或第三象限.
一、单选题
1.在平面直角坐标系中,点 关于x轴对称的点是(??? )
A.?(2,1)(2,1)??????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
2.已知点M (3,﹣2),N(﹣3,﹣2),则直线MN与x轴、y轴的位置关系分别为(? )
A.?平行,垂直???????????????????????B.?平行,平行???????????????????????C.?垂直,平行???????????????????????D.?相交,相交
3.如图,在平面直角坐标系中,点 A(3,m)A(3,m) 在第一象限,若点A关于x轴的对称点B在直线 上,则m的值为(??? )
A.?-1???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
4.平面直角坐标中,已知点P(a , 3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( ???)
A.?(﹣a , 3)??????????????????B.?(a , ﹣3)??????????????????C.?(﹣a+2,3)??????????????????D.?(﹣a+4,3)
二、填空题
5.如图,点 与点 Q(a,b)Q(a,b) 关于直线 对称,则 a+b=a+b= ________.
6.点A(-2,1)关于x轴对称的点的坐标是________.
三、作图题
7.如图,在由长度为1个单位长度的小正方形组成的网格中, 的三个顶点A,B,C都在格点上,分别按下列要求在网格中作图:
( 1 )画出与 关于直线l成轴对称的 ;
( 2 )在直线l上找出一点P,使得 的值最大;(保留作图痕迹,并标上字母P)
( 3 )在直线l上找出一点Q,使得 QA+QC1QA+QC1 的值最小.(保留作图痕迹,并标上字母Q)
8.如图,网格中的 与 为轴对称图形,且顶点都在格点上.
(1)利用网格,作出 与 的对称轴l;
(2)结合图形,在对称轴l上画出一点 PP ,使得 PA+PCPA+PC 最小;
(3)如果每个小正方形的边长为1,请直接写出 的面积.
9.如图,在平面直角坐标系 xoyxoy 中,A(-1,5),B(-1,0),C(-4,3)
(1)在图中作出 关于 yy 轴的对称图形 .
(2)写出点 的坐标.
(3)求出 的面积.
10.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
①在如图所示的网格平面内作出平面直角坐标系;
②作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
③P是x轴上的动点,在图中找出使△A′BP周长最短时的点P,直接写出点P的坐标.
四、综合题
11.在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB =OA=3.
(1)求点A、B的坐标;
(2)已知点C(-2,2),求△ BOCBOC 的面积;
(3)点P是第一、三象限角平分线上一点,若 ,求点P的坐标.
?
12.在平面直角坐标系中,有点A(a﹣1,3),B(a+2,2a﹣1)
(1)若线段AB∥x轴,求点A、B的坐标;
(2)当点B到y轴的距离与点A到x轴的距离相等时,求点B所在的象限.
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 A
3.【答案】 C
4.【答案】 D
二、填空题
5.【答案】 -5
6.【答案】 (-2,-1)
三、作图题
7.【答案】 解:(1)如图, 即为所求.
( 2 )如图,连接 AC1AC1 并延长,交直线l于点P,点P即为所求.
∵点C1点C关于直线l对称,
∴ =AC1 ,
∴连接 AC1AC1 并延长,交直线l于点P,点P即为所求.
( 3 )如图,直线 ACAC 与直线l的交点Q即为所求,
∵点C1点C关于直线l对称,
∴ QA+QC1QA+QC1 =QA+QC=AC,
∴直线 ACAC 与直线l的交点Q.
8.【答案】 (1)解:对称轴应为两个三角形对应点连线的中线,故连接CF、DE,找到线段CF、DE的中点,再连接起来,即为所求直线l.
(2)解:如图所示,点P即为所求;
连接CD与l的交点即为点P的位置,因为点A与点D关于l对称,根据两点之间,线段最短可得: PA+PC=PD+PC=CDPA+PC=PD+PC=CD ,即P点即为所求;
(3)解: ABC的面积可由一个矩形,减去三个直角三角形的面积所得,
,
故 ABC的面积为3.
9.【答案】 (1)解:所作图形如图所示:
(2)解:点 A1A1 , B1B1 , C1C1 的坐标分别为(1,5),(1,0),(4,3)
(3)解:∵A(-1,5),B(-1,0),C(-4,3),∴ = =7.5
10.【答案】 解:如图所示,B′(2,1)、点P即为所求点,
设直线A′B1的解析式为y=kx+b(k≠0),
∵A′(4,5),B1(﹣2,﹣1),
∴ 解得 {k=1b=1{k=1b=1
∴直线A′B1的解析式为y=x+1.
∵当y=0时,x+1=0,解得x=﹣1,
∴P(﹣1,0)
四、综合题
11.【答案】 (1)∵OB=OA=3,A、B两点分别在x轴、y轴的正半轴上, ∴A(3,0),B(0,3).
(2) =3.
(3)∵点P是第一、三象限角平分线上,∴设P(a,a). ∵ ,
当 P1P1 在AB的上方第一象限时,
= .
= .
∴ . 整理,得 .∴ a=7a=7 . ∴ P1P1 (7,7).
12.【答案】 (1)∵线段AB∥x轴,
∴2a﹣1=3,
解得:a=2,
故a﹣1=1,a+2=4,
则A(1,3),B(4,3);
(2)∵点B到y轴的距离与点A到x轴的距离相等,
∴|a+2|=3,
解得:a=﹣5或1,
当a=﹣5时
故a+2=﹣3,2a﹣1=﹣11,
故B(﹣3,﹣11)在第三象限,
当a=1时
故a+2=3,2a﹣1=1,
故B(3,1)在第一象限,
综上所述:点B在第一象限或第三象限.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
