2020-2021学年北师大版数学九年级下册1.4 解直角三角形 课时同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版数学九年级下册1.4 解直角三角形 课时同步练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 409.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 00:00:00 | ||
图片预览

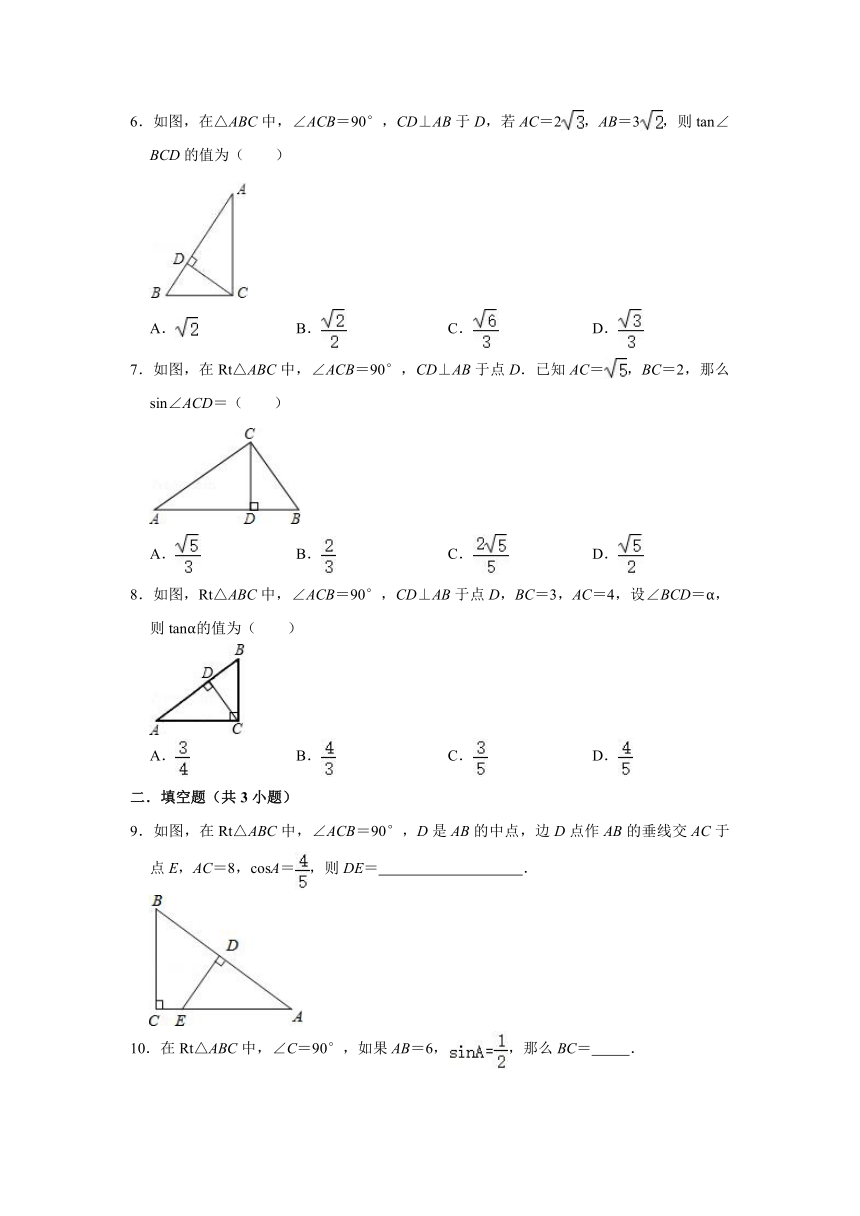

文档简介
《1.4 解直角三角形》课时同步练习2020-2021学年北师大版数学九(下)
一.选择题(共8小题)
1.如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为,则y的值为( )
A.4 B. C.5 D.6
2.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
3.如图,Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长是( )
A.3 B.4 C.5 D.6
4.在Rt△ABC中,∠C=90°,若∠A=30°,则三边的比a:b:c等于( )
A.1:2:3 B.1::2 C.1:1: D.1::2
5.如图,菱形ABCD的周长为40cm,DE⊥AB,垂足为E,sinA=,则下列结论正确的有( )
①DE=6cm;②BE=2cm;③菱形面积为60cm2;④BD=cm.
A.1个 B.2个 C.3个 D.4个
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,AB=3,则tan∠BCD的值为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
8.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,设∠BCD=α,则tanα的值为( )
A. B. C. D.
二.填空题(共3小题)
9.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,边D点作AB的垂线交AC于点E,AC=8,cosA=,则DE= .
10.在Rt△ABC中,∠C=90°,如果AB=6,,那么BC= .
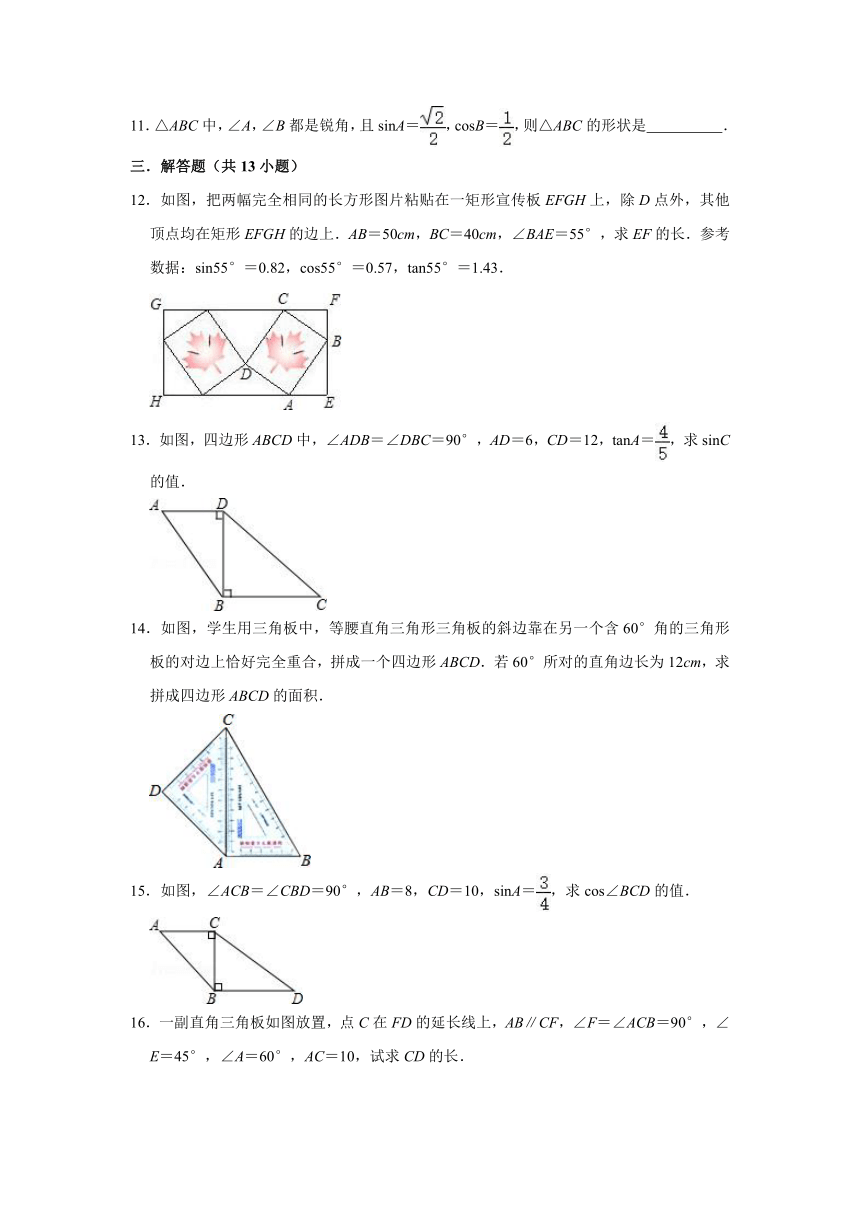
11.△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则△ABC的形状是 .
三.解答题(共13小题)
12.如图,把两幅完全相同的长方形图片粘贴在一矩形宣传板EFGH上,除D点外,其他顶点均在矩形EFGH的边上.AB=50cm,BC=40cm,∠BAE=55°,求EF的长.参考数据:sin55°=0.82,cos55°=0.57,tan55°=1.43.
13.如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA=,求sinC的值.
14.如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.
15.如图,∠ACB=∠CBD=90°,AB=8,CD=10,sinA=,求cos∠BCD的值.
16.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
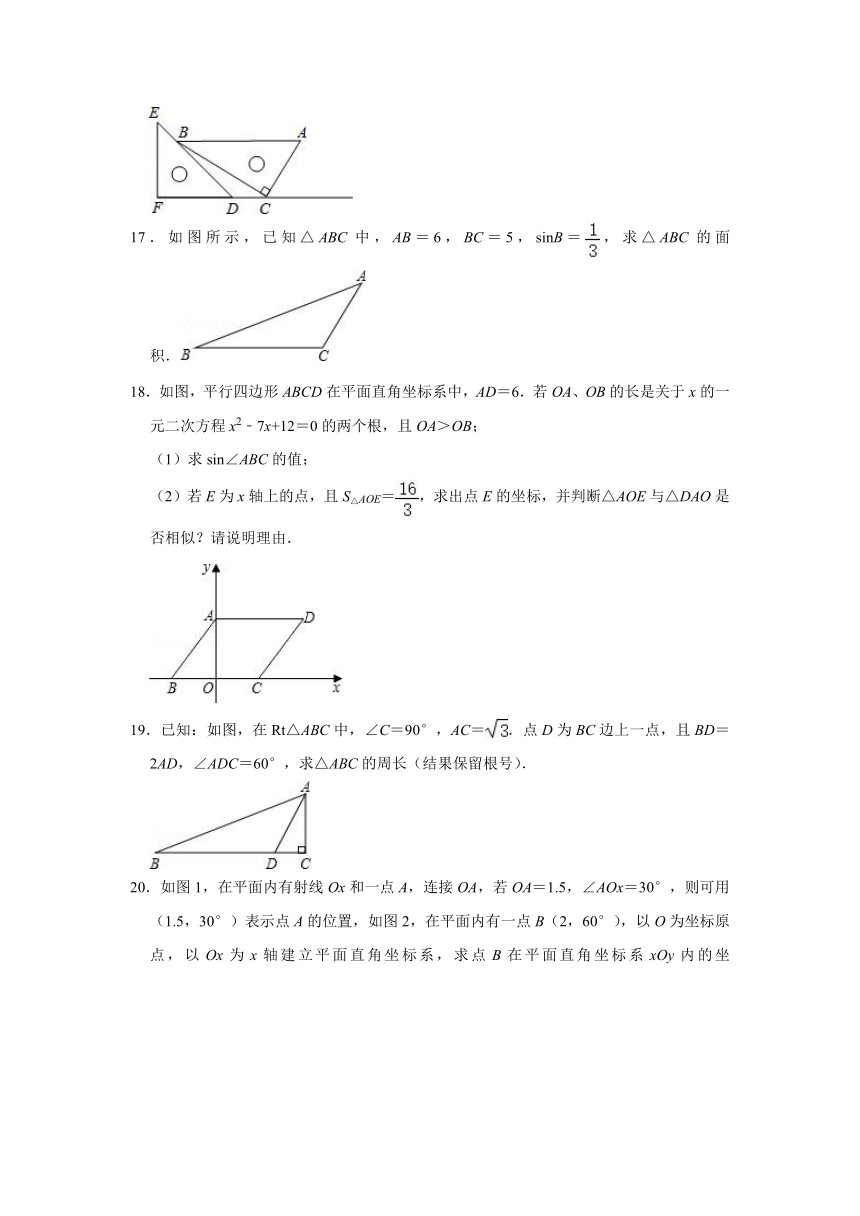
17.如图所示,已知△ABC中,AB=6,BC=5,sinB=,求△ABC的面积.
18.如图,平行四边形ABCD在平面直角坐标系中,AD=6.若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB;
(1)求sin∠ABC的值;
(2)若E为x轴上的点,且S△AOE=,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由.
19.已知:如图,在Rt△ABC中,∠C=90°,AC=.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).
20.如图1,在平面内有射线Ox和一点A,连接OA,若OA=1.5,∠AOx=30°,则可用(1.5,30°)表示点A的位置,如图2,在平面内有一点B(2,60°),以O为坐标原点,以Ox为x轴建立平面直角坐标系,求点B在平面直角坐标系xOy内的坐标.
21.在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由;
(3)在(2)的情况下,求ED的长.
22.图中有两个正方形,A、C两点在大正方形的对角线上,△HAC是等边三角形.若AB=2,求EF的长.(参考数据:sin30°=,cos30°=,tan30°=;sin45°=,cos45°=,tan45°=1)
23.在Rt△ABC中,∠C=90°,c=8,∠A=60°.求△ABC的面积.
24.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D在AB上,AD=2,点E,F同时从点D出发,分别沿DA、DB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止,在点E,F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒,正方形EFGH与△ABC重叠部分面积为S.
(1)当0<t<2时,求正方形EFGH的顶点刚好落在线段AC上时t的值;
(2)当t≥2时,直接写出当△EGB为等腰三角形时t的值.
参考答案
一.选择题(共8小题)
1.解:作AB⊥x轴于点B,如下图所示:
∵tanα=,tanα=,
∴y=6.
故选项A错误,选项B错误,选项C错误,选项D正确.
故选:D.
2.解:∵cos∠B=,
∴∠B=45°,
当△ABC为钝角三角形时,如图1,
∵AB=12,∠B=45°,
∴AD=BD=12,
∵AC=13,
∴由勾股定理得CD=5,
∴BC=BD﹣CD=12﹣5=7;
当△ABC为锐角三角形时,如图2,
BC=BD+CD=12+5=17,
故选:D.
3.解:∵∠C=90°,sinA=,AB=5,
∴BC=AB×sinA=5×=3,
由勾股定理得:
AC==4.
故选:B.
4.解:在Rt△ABC中,∵∠C=90°,∠A=30°,
∴a=c,cos30°==,
∴c=2a,b=c=a
a:b:c=a:a:2a=1::2.
故选:B.
5.解:∵菱形ABCD的周长为40cm,
∴AD=AB=BC=CD=10.
∵DE⊥AB,垂足为E,
sinA===,
∴DE=6cm,AE=8cm,BE=2cm.
∴菱形的面积为:AB×DE=10×6=60cm2.
在三角形BED中,
BE=2cm,DE=6cm,BD=2cm,∴①②③正确,④错误;=2
∴结论正确的有三个.
故选:C.
6.解:由勾股定理知,c2=a2+b2
∴BC==.
根据同角的余角相等,∠BCD=∠A.
∴tan∠BCD=tan∠A==.
故选:B.
7.解:在Rt△ABC中,
∵AB2=AC2+BC2,∴AB=3.
∵∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B.
∴sin∠ACD=sinB==.
故选:A.
8.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠B=90°,∠A+∠B=90°,
∴∠BCD=∠A=α.
∴tanα=tanA==.
故选:A.
二.填空题(共3小题)
9.解:∵在Rt△ABC中,∠ACB=90°,AC=8,cosA=,cosA=,
∴AB=10,BC=.
∴tanA=.
∵D是AB的中点,
∴AD==5.
∵ED⊥AB,
∴∠EDA=90°.
∵tanA=,AD=5,
∴DE=.
10.解:Rt△ABC中,∠C=90°,AB是斜边,
∵AB=6,,
∴BC=AB?sinA=6×=3.
11.解:∵sinA=,cosB=,
∴∠A=45°,∠B=60°,
∴∠C=75°,
∴△ABC的形状是锐角三角形.
故答案为:锐角三角形.
三.解答题(共13小题)
12.解:在直角三角形ABE中,AB=50cm,∠BAE=55°,
∴BE=AB?sin∠BAE=50?sin55°=50×0.82=41.
∵ABCD是矩形,
∴∠CBF=∠BAE=55°,
∴在直角三角形BCF中,BC=40cm,∠CBF=55°,
∴BF=BC?cos∠CBF=40?cos55°=40×0.57=22.8.
∴EF=BE+BF=41+22.8=63.8.
所以EF的长为63.8cm.
13.解:∵∠ADB=∠DBC=90°,AD=6,tanA=,tanA=,
∴BD=4.8.
∵CD=12,
∴sinC=.
14.解:∵在Rt△ACD中,∠D=90°,∠ACD=∠CAD=45°,
∴AD=CD=AC=6.
∵在Rt△ABC中,∠CAB=90°,∠B=60°,
∴AB=AC=4.
∵S△ACD=AD?CD=×6×6=36,
S△ABC=AB?AC=×4×12=24,
∴四边形ABCD的面积=S△ACD+S△ABC=36+24(cm2).
15.解:在Rt△ACB中,∠ACB=90°,
则BC=AB?sinA=8×=6,
在Rt△DBC中,∠CBD=90°,
cos∠BCD===.
16.解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC×tan60°=10,
∵AB∥CF,
∴BM=BC×sin30°=10×=5,
CM=BC×cos30°=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM﹣MD=15﹣5.
17.解:如图,作AD⊥BC的延长线于D;
由题意得:AB=6,sinB=,则AD=AB?sinB=6×=2;
又BC=5,则S△ABC=×BC×AD=×5×2=5;
故△ABC的面积为5.
18.解:(1)解方程:x2﹣7x+12=0
解得x1=3,x2=4(1分)
∵OA>OB
∴OA=4,OB=3(2分)
由勾股定理得出:
∴AB=5(3分)
∴在Rt△OAB中,sin∠ABC==(4分)
(2)①∵S△AOE=
∴OA?OE=
∴OE=(5分)
∴点E的坐标为(﹣,0)或(,0)(6分)
②△AOE与△DAO相似,理由如下:
∵=,
∴
∵∠AOE=∠DAO=90°(7分)
∴△AOE∽△DAO.(8分)
19.解:在Rt△ADC中,
∵sin∠ADC=,
∴AD===2.
∴BD=2AD=4,
∵tan∠ADC=,DC===1,
∴BC=BD+DC=5.
在Rt△ABC中,AB==2,
∴△ABC的周长=AB+BC+AC=2+5+.
20.解:作BC⊥OX于点C,
∵OB=2,∠BOX=60°,
∴OC=OB×cos60°=1,BC=OB×sin60°=,
∴点B在平面直角坐标系xOy内的坐标为:(1,).
21.解:(1)EA1=FC.
证明:(证法一)∵AB=BC,
∴∠A=∠C.
由旋转可知,AB=BC1,∠A=∠C1,∠ABE=∠C1BF,
∴△ABE≌△C1BF.
∴BE=BF,又∵BA1=BC,
∴BA1﹣BE=BC﹣BF.即EA1=FC.
(证法二)∵AB=BC,∴∠A=∠C.
由旋转可知,∠A1=∠C,A1B=CB,而∠EBC=∠FBA1,
∴△A1BF≌△CBE.
∴BE=BF,∴BA1﹣BE=BC﹣BF,
即EA1=FC.
(2)四边形BC1DA是菱形.
证明:∵∠A1=∠ABA1=30°,
∴A1C1∥AB,同理AC∥BC1.
∴四边形BC1DA是平行四边形.
又∵AB=BC1,
∴四边形BC1DA是菱形.
(3)(解法一)过点E作EG⊥AB于点G,则AG=BG=1.
在Rt△AEG中,AE=.
由(2)知四边形BC1DA是菱形,
∴AD=AB=2,
∴ED=AD﹣AE=2﹣.
(解法二)∵∠ABC=120°,∠ABE=30°,∴∠EBC=90°.
在Rt△EBC中,BE=BC?tanC=2×tan30°=.
∴EA1=BA1﹣BE=2﹣.
∵A1C1∥AB,
∴∠A1DE=∠A.
∴∠A1DE=∠A1.
∴ED=EA1=2﹣.
22.解:在小正方形ABCD中,AB=2,则AC=2,
在等边三角形ACH中,CH=2,CO=,HO=,
在等腰直角三角形HOG中,HG=2,
即EF=2.
23.解:∵在Rt△ABC中,∠C=90°,c=8,∠A=60°.
∴BC=12,AC=4,
∴△ABC的面积=.
24.解:(1)①当点G落在线段AC上时,如图1所示:
则GF=2t,AF=2+t
∵∠AFG=∠ACB=90°,∠A=∠A,
∴△AFG∽△ACB,
∴=,
即=,
解得:t=;
②当点H落在线段AC上时,如图2所示:
则AE=2﹣t,EH=2t,
∵∠AEH=∠ACB=90°,∠A=∠A,
∴△AEH∽△ACB,
∴=,
即=,
解得:t=;
∴当0<t<2时,正方形EFGH的顶点刚好落在线段AC上时t的值为秒或秒;
(2)当t≥2时,△EGB为等腰三角形,如图3所示:
则EF=4,
∵四边形EFGH为正方形,
∴EG=EF=4,
由题意得:BE=8+2﹣(t﹣2)=12﹣t,BF=8﹣t,
∴BG===,
①当EG=BE时,4=12﹣t,∴t=12﹣4;
②当GE=GB时,4=,
解得:t1=4,t2=12(不合题意舍去);
③当BE=BG时,12﹣t=,
解得:t=8;
综上所述,当t≥2时,△EGB为等腰三角形时t的为12﹣4或4或8.
一.选择题(共8小题)
1.如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为,则y的值为( )
A.4 B. C.5 D.6
2.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7 B.8 C.8或17 D.7或17
3.如图,Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长是( )
A.3 B.4 C.5 D.6
4.在Rt△ABC中,∠C=90°,若∠A=30°,则三边的比a:b:c等于( )
A.1:2:3 B.1::2 C.1:1: D.1::2
5.如图,菱形ABCD的周长为40cm,DE⊥AB,垂足为E,sinA=,则下列结论正确的有( )
①DE=6cm;②BE=2cm;③菱形面积为60cm2;④BD=cm.
A.1个 B.2个 C.3个 D.4个
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,AB=3,则tan∠BCD的值为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
8.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,设∠BCD=α,则tanα的值为( )
A. B. C. D.
二.填空题(共3小题)
9.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,边D点作AB的垂线交AC于点E,AC=8,cosA=,则DE= .
10.在Rt△ABC中,∠C=90°,如果AB=6,,那么BC= .
11.△ABC中,∠A,∠B都是锐角,且sinA=,cosB=,则△ABC的形状是 .
三.解答题(共13小题)
12.如图,把两幅完全相同的长方形图片粘贴在一矩形宣传板EFGH上,除D点外,其他顶点均在矩形EFGH的边上.AB=50cm,BC=40cm,∠BAE=55°,求EF的长.参考数据:sin55°=0.82,cos55°=0.57,tan55°=1.43.
13.如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA=,求sinC的值.
14.如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.
15.如图,∠ACB=∠CBD=90°,AB=8,CD=10,sinA=,求cos∠BCD的值.
16.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
17.如图所示,已知△ABC中,AB=6,BC=5,sinB=,求△ABC的面积.
18.如图,平行四边形ABCD在平面直角坐标系中,AD=6.若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB;
(1)求sin∠ABC的值;
(2)若E为x轴上的点,且S△AOE=,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由.
19.已知:如图,在Rt△ABC中,∠C=90°,AC=.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长(结果保留根号).
20.如图1,在平面内有射线Ox和一点A,连接OA,若OA=1.5,∠AOx=30°,则可用(1.5,30°)表示点A的位置,如图2,在平面内有一点B(2,60°),以O为坐标原点,以Ox为x轴建立平面直角坐标系,求点B在平面直角坐标系xOy内的坐标.
21.在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由;
(3)在(2)的情况下,求ED的长.
22.图中有两个正方形,A、C两点在大正方形的对角线上,△HAC是等边三角形.若AB=2,求EF的长.(参考数据:sin30°=,cos30°=,tan30°=;sin45°=,cos45°=,tan45°=1)
23.在Rt△ABC中,∠C=90°,c=8,∠A=60°.求△ABC的面积.
24.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D在AB上,AD=2,点E,F同时从点D出发,分别沿DA、DB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止,在点E,F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒,正方形EFGH与△ABC重叠部分面积为S.
(1)当0<t<2时,求正方形EFGH的顶点刚好落在线段AC上时t的值;
(2)当t≥2时,直接写出当△EGB为等腰三角形时t的值.
参考答案
一.选择题(共8小题)
1.解:作AB⊥x轴于点B,如下图所示:
∵tanα=,tanα=,
∴y=6.
故选项A错误,选项B错误,选项C错误,选项D正确.
故选:D.
2.解:∵cos∠B=,
∴∠B=45°,
当△ABC为钝角三角形时,如图1,
∵AB=12,∠B=45°,
∴AD=BD=12,
∵AC=13,
∴由勾股定理得CD=5,
∴BC=BD﹣CD=12﹣5=7;
当△ABC为锐角三角形时,如图2,
BC=BD+CD=12+5=17,
故选:D.
3.解:∵∠C=90°,sinA=,AB=5,
∴BC=AB×sinA=5×=3,
由勾股定理得:
AC==4.
故选:B.
4.解:在Rt△ABC中,∵∠C=90°,∠A=30°,
∴a=c,cos30°==,
∴c=2a,b=c=a
a:b:c=a:a:2a=1::2.
故选:B.
5.解:∵菱形ABCD的周长为40cm,
∴AD=AB=BC=CD=10.
∵DE⊥AB,垂足为E,
sinA===,
∴DE=6cm,AE=8cm,BE=2cm.
∴菱形的面积为:AB×DE=10×6=60cm2.
在三角形BED中,
BE=2cm,DE=6cm,BD=2cm,∴①②③正确,④错误;=2
∴结论正确的有三个.
故选:C.
6.解:由勾股定理知,c2=a2+b2
∴BC==.
根据同角的余角相等,∠BCD=∠A.
∴tan∠BCD=tan∠A==.
故选:B.
7.解:在Rt△ABC中,
∵AB2=AC2+BC2,∴AB=3.
∵∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B.
∴sin∠ACD=sinB==.
故选:A.
8.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠B=90°,∠A+∠B=90°,
∴∠BCD=∠A=α.
∴tanα=tanA==.
故选:A.
二.填空题(共3小题)
9.解:∵在Rt△ABC中,∠ACB=90°,AC=8,cosA=,cosA=,
∴AB=10,BC=.
∴tanA=.
∵D是AB的中点,
∴AD==5.
∵ED⊥AB,
∴∠EDA=90°.
∵tanA=,AD=5,
∴DE=.
10.解:Rt△ABC中,∠C=90°,AB是斜边,
∵AB=6,,
∴BC=AB?sinA=6×=3.
11.解:∵sinA=,cosB=,
∴∠A=45°,∠B=60°,
∴∠C=75°,
∴△ABC的形状是锐角三角形.
故答案为:锐角三角形.
三.解答题(共13小题)
12.解:在直角三角形ABE中,AB=50cm,∠BAE=55°,
∴BE=AB?sin∠BAE=50?sin55°=50×0.82=41.
∵ABCD是矩形,
∴∠CBF=∠BAE=55°,
∴在直角三角形BCF中,BC=40cm,∠CBF=55°,
∴BF=BC?cos∠CBF=40?cos55°=40×0.57=22.8.
∴EF=BE+BF=41+22.8=63.8.
所以EF的长为63.8cm.
13.解:∵∠ADB=∠DBC=90°,AD=6,tanA=,tanA=,
∴BD=4.8.
∵CD=12,
∴sinC=.
14.解:∵在Rt△ACD中,∠D=90°,∠ACD=∠CAD=45°,
∴AD=CD=AC=6.
∵在Rt△ABC中,∠CAB=90°,∠B=60°,
∴AB=AC=4.
∵S△ACD=AD?CD=×6×6=36,
S△ABC=AB?AC=×4×12=24,
∴四边形ABCD的面积=S△ACD+S△ABC=36+24(cm2).
15.解:在Rt△ACB中,∠ACB=90°,
则BC=AB?sinA=8×=6,
在Rt△DBC中,∠CBD=90°,
cos∠BCD===.
16.解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC×tan60°=10,
∵AB∥CF,
∴BM=BC×sin30°=10×=5,
CM=BC×cos30°=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM﹣MD=15﹣5.
17.解:如图,作AD⊥BC的延长线于D;
由题意得:AB=6,sinB=,则AD=AB?sinB=6×=2;
又BC=5,则S△ABC=×BC×AD=×5×2=5;
故△ABC的面积为5.
18.解:(1)解方程:x2﹣7x+12=0
解得x1=3,x2=4(1分)
∵OA>OB
∴OA=4,OB=3(2分)
由勾股定理得出:
∴AB=5(3分)
∴在Rt△OAB中,sin∠ABC==(4分)
(2)①∵S△AOE=
∴OA?OE=
∴OE=(5分)
∴点E的坐标为(﹣,0)或(,0)(6分)
②△AOE与△DAO相似,理由如下:
∵=,
∴
∵∠AOE=∠DAO=90°(7分)
∴△AOE∽△DAO.(8分)
19.解:在Rt△ADC中,
∵sin∠ADC=,
∴AD===2.
∴BD=2AD=4,
∵tan∠ADC=,DC===1,
∴BC=BD+DC=5.
在Rt△ABC中,AB==2,
∴△ABC的周长=AB+BC+AC=2+5+.
20.解:作BC⊥OX于点C,
∵OB=2,∠BOX=60°,
∴OC=OB×cos60°=1,BC=OB×sin60°=,
∴点B在平面直角坐标系xOy内的坐标为:(1,).
21.解:(1)EA1=FC.
证明:(证法一)∵AB=BC,
∴∠A=∠C.
由旋转可知,AB=BC1,∠A=∠C1,∠ABE=∠C1BF,
∴△ABE≌△C1BF.
∴BE=BF,又∵BA1=BC,
∴BA1﹣BE=BC﹣BF.即EA1=FC.
(证法二)∵AB=BC,∴∠A=∠C.
由旋转可知,∠A1=∠C,A1B=CB,而∠EBC=∠FBA1,
∴△A1BF≌△CBE.
∴BE=BF,∴BA1﹣BE=BC﹣BF,
即EA1=FC.
(2)四边形BC1DA是菱形.
证明:∵∠A1=∠ABA1=30°,
∴A1C1∥AB,同理AC∥BC1.
∴四边形BC1DA是平行四边形.
又∵AB=BC1,
∴四边形BC1DA是菱形.
(3)(解法一)过点E作EG⊥AB于点G,则AG=BG=1.
在Rt△AEG中,AE=.
由(2)知四边形BC1DA是菱形,
∴AD=AB=2,
∴ED=AD﹣AE=2﹣.
(解法二)∵∠ABC=120°,∠ABE=30°,∴∠EBC=90°.
在Rt△EBC中,BE=BC?tanC=2×tan30°=.
∴EA1=BA1﹣BE=2﹣.
∵A1C1∥AB,
∴∠A1DE=∠A.
∴∠A1DE=∠A1.
∴ED=EA1=2﹣.
22.解:在小正方形ABCD中,AB=2,则AC=2,
在等边三角形ACH中,CH=2,CO=,HO=,
在等腰直角三角形HOG中,HG=2,
即EF=2.
23.解:∵在Rt△ABC中,∠C=90°,c=8,∠A=60°.
∴BC=12,AC=4,
∴△ABC的面积=.
24.解:(1)①当点G落在线段AC上时,如图1所示:
则GF=2t,AF=2+t
∵∠AFG=∠ACB=90°,∠A=∠A,
∴△AFG∽△ACB,
∴=,
即=,
解得:t=;
②当点H落在线段AC上时,如图2所示:
则AE=2﹣t,EH=2t,
∵∠AEH=∠ACB=90°,∠A=∠A,
∴△AEH∽△ACB,
∴=,
即=,
解得:t=;
∴当0<t<2时,正方形EFGH的顶点刚好落在线段AC上时t的值为秒或秒;
(2)当t≥2时,△EGB为等腰三角形,如图3所示:
则EF=4,
∵四边形EFGH为正方形,
∴EG=EF=4,
由题意得:BE=8+2﹣(t﹣2)=12﹣t,BF=8﹣t,
∴BG===,
①当EG=BE时,4=12﹣t,∴t=12﹣4;
②当GE=GB时,4=,
解得:t1=4,t2=12(不合题意舍去);
③当BE=BG时,12﹣t=,
解得:t=8;
综上所述,当t≥2时,△EGB为等腰三角形时t的为12﹣4或4或8.
