4.3列联表独立性分析案例课件-湘教版数学选修1-2(31张PPT)
文档属性
| 名称 | 4.3列联表独立性分析案例课件-湘教版数学选修1-2(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 278.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 15:56:38 | ||
图片预览











文档简介
列联表独立性案例分析
【课标要求】
1.通过典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及其简单应用.
2.本节的重点和难点是独立性检验的思想、方法及其初步应用.
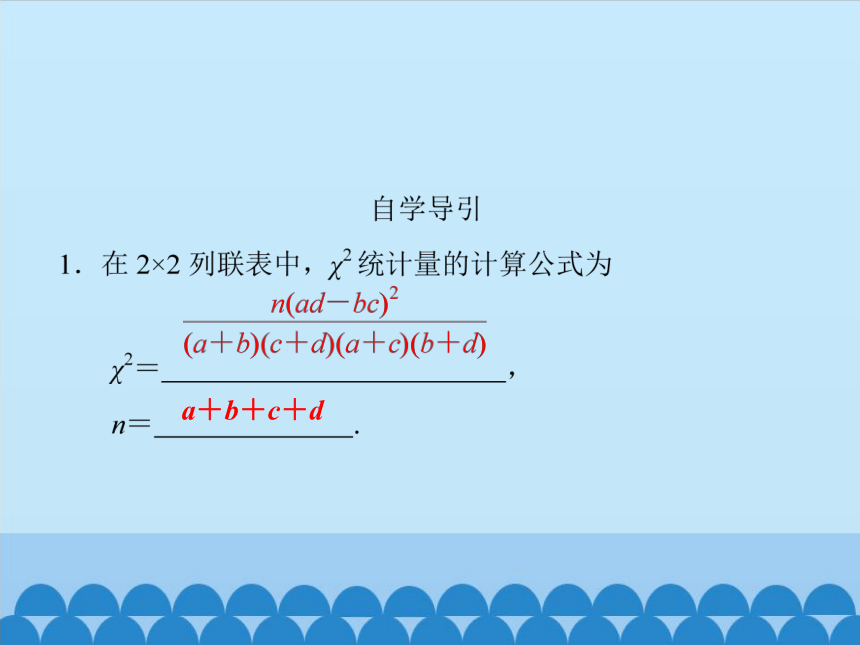
a+b+c+d
2.当根据具体的数据算出的χ2>3.841时,有 的把握说事件A与B ;当χ2>6.635时,有 的把握说事件A与B ,当χ2≤3.841时,认为事件A与B是 的.
95%
有关
99%
有关
无关
什么是独立性检验的基本思想?
提示 独立性检验的基本思想类似于反证法, 要确认“两个分类变量有关系”这一结论成立的可信度,首先假设该结论不成立,即假设结论“两个分类变量没有关系”成立,在该假设下构建的随机变量χ2应该很小.如果由观测数据计算得到的χ2的观测值很大,则在一定程度上说明假设不合理.
自主探究
答案 A
2.在一个2×2列联表中,由其数据计算得χ2=13.097,则其两个变量间有关系的可能性为 ( ).
A.99% B.95%
C.90% D.无关系
解析 因为χ2=13.097,13.097>6.635,所以两个变量间有关系的可能性为99%.
答案 A
3.用χ2统计量进行独立性检验时,使用的表称为________,要求表中的四个数据均大于________.
答案 2×2列联表 5
4.下面是一个2×2列联表:
则表中a、b处的值分别为______、______.
解析 a+25=45,∴a=20,又a+6=b,∴b=26.
答案 20 26
y1
y2
总计
x1
a
25
45
x2
6
32
38
总 计
b
57
一般地,如果事件A1、A2、…,An相互独立,那么这n个事件同时发生的概率等于每个事件发生的概率的乘积,即P(A1A2…An)=P(A1)P(A2)…P(An).
经过对χ2统计量分布的研究,已经得到了两个临界值:
3.841与6.635.当根据具体的数据算出的χ2>3.841时,有95%的把握说事件A与B有关;当χ2>6.635时,有99%的把握说事件A与B有关;当χ2≤3.841时,认为事件A与B是无关的.
反证法原理——在假设H0下,如果推出一个矛盾,就证明了H0不成立.
独立性检验原理——在假设H0下,如果出现一个与H0相矛盾的小概率事件,就推断H0不成立,且该推断犯错误的概率不超过小概率.
3.反证法原理与独立性检验原理的比较
题型一 两个事件的独立性检验
【例1】 某推销商为某保健药品做广告,在广告中宣传“在服用该药品的105人中有100人未患A疾病”.经调查发现,在不服用该药品的418人中仅有18人患A疾病,请用所学知识分析该药品对患A疾病是否有效?
典例剖析
解 将问题中的数据写成2×2列联表:
患A疾病
不患A疾病
合计
服用该药品
5
100
105
不服用该药品
18
400
418
合计
23
500
523
方法点评 (1)利用独立性假设可以帮助我们定量分析两个分类变量之间是否有关系,因此利用它可以帮助我们理性地看待广告中的某些数字,从而不被某些虚假广告所蒙骗.
(2)独立性检验的一般步骤:
①根据样本数据制成2×2列联表;
②根据公式,计算χ2的值;
③比较χ2与临界值3.841与6.635的大小,作统计推断.
【训练1】 在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.请用独立性检验方法判断秃顶与患心脏病是否有关系?
解 根据题目所给数据得到如下列联表:
秃顶与患心脏病列联表
患心脏病
患其他病
总 计
秃 顶
214
175
389
不秃顶
451
597
1 048
总 计
665
772
1 437
题型二 独立性检验的综合应用
【例2】 某市对该市一重点中学2010年高考上线情况进行统计,随机抽查244名学生,得到如下表格:
语文
数学
英语
综合科目
上线
不上线
上线
不上线
上线
不上线
上线
不上线
总分上线201人
174
27
178
23
176
25
175
26
续表
试求各科上线与总分上线之间的关系,并求出哪一科目与总分上线关系最大?
总分不上线43人
30
13
23
20
24
19
26
17
总计
204
40
201
43
200
44
201
43
方法点评 在掌握了独立性检验的基本思想后我们一般通过计算χ2的值,然后比较χ2值与临界值的大小来较精确地给出“两个分类变量”的可靠程度.
【训练2】 某校高三年级在一次全年级的大型考试中,数学成绩优秀和非优秀的学生中,物理、化学也为优秀的人数如下表所示,则数学成绩优秀与物理、化学也优秀哪个关系较大?
注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.
物理
化学
数学优秀
228
225
数学非优秀
143
156
解 (1)列出数学与物理优秀的2×2列联表如下:
将表中数据代入公式χ2得χ2≈270.114.
物理优秀
物理非优秀
合计
数学优秀
228
132
360
数学非优秀
143
737
880
合计
371
869
1 240
(2)列出数学与化学优秀的2×2列联表如下:
将表中数据代入公式计算得χ2≈240.611.
由上面分析可知,数学成绩优秀与物理、化学优秀都有关系,由计算χ2的值都大于6.635,可以说明都有99%的把握认为数学优秀与物理、化学优秀有关系,但与物理关系最大,化学其次.
化学优秀
化学非优秀
合计
数学优秀
225
135
360
数学非优秀
156
724
880
合计
381
859
1 240
误区警示 不能准确理解两个变量相关的统计
含义导致错误
【例3】 考察棉花种子是否经过处理跟生病之间的关系得到如下数据:
种子经过处理
种子未经过处理
合计
生病
32
101
133
不生病
61
213
274
合计
93
314
407
根据数据可以判断 ( ).
A.种子是否经过处理跟是否生病有关
B.种子是否经过处理跟是否生病无关
C.种子是否经过处理决定是否生病
D.以上都是错误的
[错解] 因为种子经过处理后,生病的可能性会变小,故选A.
[正解] B
纠错心得 本题是利用χ2公式求出χ2的值,再利用与临界值的大小关系来判断假设是否成立,解题时应注意准确代数与计算,不可错用公式,要准确进行比较与判断.
谢谢!
【课标要求】
1.通过典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及其简单应用.
2.本节的重点和难点是独立性检验的思想、方法及其初步应用.
a+b+c+d
2.当根据具体的数据算出的χ2>3.841时,有 的把握说事件A与B ;当χ2>6.635时,有 的把握说事件A与B ,当χ2≤3.841时,认为事件A与B是 的.
95%
有关
99%
有关
无关
什么是独立性检验的基本思想?
提示 独立性检验的基本思想类似于反证法, 要确认“两个分类变量有关系”这一结论成立的可信度,首先假设该结论不成立,即假设结论“两个分类变量没有关系”成立,在该假设下构建的随机变量χ2应该很小.如果由观测数据计算得到的χ2的观测值很大,则在一定程度上说明假设不合理.
自主探究
答案 A
2.在一个2×2列联表中,由其数据计算得χ2=13.097,则其两个变量间有关系的可能性为 ( ).
A.99% B.95%
C.90% D.无关系
解析 因为χ2=13.097,13.097>6.635,所以两个变量间有关系的可能性为99%.
答案 A
3.用χ2统计量进行独立性检验时,使用的表称为________,要求表中的四个数据均大于________.
答案 2×2列联表 5
4.下面是一个2×2列联表:
则表中a、b处的值分别为______、______.
解析 a+25=45,∴a=20,又a+6=b,∴b=26.
答案 20 26
y1
y2
总计
x1
a
25
45
x2
6
32
38
总 计
b
57
一般地,如果事件A1、A2、…,An相互独立,那么这n个事件同时发生的概率等于每个事件发生的概率的乘积,即P(A1A2…An)=P(A1)P(A2)…P(An).
经过对χ2统计量分布的研究,已经得到了两个临界值:
3.841与6.635.当根据具体的数据算出的χ2>3.841时,有95%的把握说事件A与B有关;当χ2>6.635时,有99%的把握说事件A与B有关;当χ2≤3.841时,认为事件A与B是无关的.
反证法原理——在假设H0下,如果推出一个矛盾,就证明了H0不成立.
独立性检验原理——在假设H0下,如果出现一个与H0相矛盾的小概率事件,就推断H0不成立,且该推断犯错误的概率不超过小概率.
3.反证法原理与独立性检验原理的比较
题型一 两个事件的独立性检验
【例1】 某推销商为某保健药品做广告,在广告中宣传“在服用该药品的105人中有100人未患A疾病”.经调查发现,在不服用该药品的418人中仅有18人患A疾病,请用所学知识分析该药品对患A疾病是否有效?
典例剖析
解 将问题中的数据写成2×2列联表:
患A疾病
不患A疾病
合计
服用该药品
5
100
105
不服用该药品
18
400
418
合计
23
500
523
方法点评 (1)利用独立性假设可以帮助我们定量分析两个分类变量之间是否有关系,因此利用它可以帮助我们理性地看待广告中的某些数字,从而不被某些虚假广告所蒙骗.
(2)独立性检验的一般步骤:
①根据样本数据制成2×2列联表;
②根据公式,计算χ2的值;
③比较χ2与临界值3.841与6.635的大小,作统计推断.
【训练1】 在某医院,因为患心脏病而住院的665名男性病人中,有214人秃顶,而另外772名不是因为患心脏病而住院的男性病人中有175人秃顶.请用独立性检验方法判断秃顶与患心脏病是否有关系?
解 根据题目所给数据得到如下列联表:
秃顶与患心脏病列联表
患心脏病
患其他病
总 计
秃 顶
214
175
389
不秃顶
451
597
1 048
总 计
665
772
1 437
题型二 独立性检验的综合应用
【例2】 某市对该市一重点中学2010年高考上线情况进行统计,随机抽查244名学生,得到如下表格:
语文
数学
英语
综合科目
上线
不上线
上线
不上线
上线
不上线
上线
不上线
总分上线201人
174
27
178
23
176
25
175
26
续表
试求各科上线与总分上线之间的关系,并求出哪一科目与总分上线关系最大?
总分不上线43人
30
13
23
20
24
19
26
17
总计
204
40
201
43
200
44
201
43
方法点评 在掌握了独立性检验的基本思想后我们一般通过计算χ2的值,然后比较χ2值与临界值的大小来较精确地给出“两个分类变量”的可靠程度.
【训练2】 某校高三年级在一次全年级的大型考试中,数学成绩优秀和非优秀的学生中,物理、化学也为优秀的人数如下表所示,则数学成绩优秀与物理、化学也优秀哪个关系较大?
注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.
物理
化学
数学优秀
228
225
数学非优秀
143
156
解 (1)列出数学与物理优秀的2×2列联表如下:
将表中数据代入公式χ2得χ2≈270.114.
物理优秀
物理非优秀
合计
数学优秀
228
132
360
数学非优秀
143
737
880
合计
371
869
1 240
(2)列出数学与化学优秀的2×2列联表如下:
将表中数据代入公式计算得χ2≈240.611.
由上面分析可知,数学成绩优秀与物理、化学优秀都有关系,由计算χ2的值都大于6.635,可以说明都有99%的把握认为数学优秀与物理、化学优秀有关系,但与物理关系最大,化学其次.
化学优秀
化学非优秀
合计
数学优秀
225
135
360
数学非优秀
156
724
880
合计
381
859
1 240
误区警示 不能准确理解两个变量相关的统计
含义导致错误
【例3】 考察棉花种子是否经过处理跟生病之间的关系得到如下数据:
种子经过处理
种子未经过处理
合计
生病
32
101
133
不生病
61
213
274
合计
93
314
407
根据数据可以判断 ( ).
A.种子是否经过处理跟是否生病有关
B.种子是否经过处理跟是否生病无关
C.种子是否经过处理决定是否生病
D.以上都是错误的
[错解] 因为种子经过处理后,生病的可能性会变小,故选A.
[正解] B
纠错心得 本题是利用χ2公式求出χ2的值,再利用与临界值的大小关系来判断假设是否成立,解题时应注意准确代数与计算,不可错用公式,要准确进行比较与判断.
谢谢!
同课章节目录
